基于改进TOPSIS法的火电厂混煤掺烧方案选择

张杨悦，王东风

（华北电力大学，河北 保定 071000）

0 引言

近年来各种基于新能源的电厂得以建立，但以燃煤为主的火力发电仍占我国总发电量的很高比例。尽管我国能源储存量很大，但是资源分配不合理，火力发电在很长一段时间内仍将是主要的发电方式。与世界先进水平相比，我国火电厂的煤炭热能利用率较低，不但造成了极大的资源浪费，还影响发电厂的安全经济运行［1-2］。当今，我国大多数火力发电厂大多选用混煤掺烧的方式来处理这一困扰。混煤掺烧将两种或多种不同的特性的煤炭按一定比例混合，使混合后的燃煤特性满足设计要求，充分利用煤炭资源，以确保机组安全经济运行，但确定一个合适的配比仍是需要研究的问题。

在灰分、挥发分、着火温度、灰熔点、发热量和成本6个性能指标下，综合考量8种预选方案的经济效益和社会效益，一般处理这种多属性决策问题的方式有层次分析法（AHP）、字典序法、加权积法、加权和法、方案排队法、ELECTRE 法、TOPSIS 法［3］。 其中TOPSIS法是解决多属性决策问题的一种常用方法，自提出以来被广泛应用于各种领域。文献［4］使用TOPSIS法解决企业协作创新伙伴的选取要求；文献［5］为评估光伏发电事项的危害将TOPSIS法与灰色关联度法相联合；文献［6］采用熵权TOPSIS法评判环境友好型都市发展建设。文献［7］采用熵权法客观地确定指标权重，基于TOPSIS法建立了基于熵权TOPSIS法的人类综合发展综合评价模型；文献［8］将熵权法运用于电力企业的竞争力评价中，可以客观地确定评价指标的权重。同时，对常规的TOPSIS方法中的决策矩阵进行了改进，解决了常规TOPSIS方法中决策矩阵复杂的缺点，简化了正负理想解的计算。

在解决多属性问题时，TOPSIS法借用理想解和负理想解给方案集X中的各个方案实行排列，其主旨在于各项指标权重的选择。目前常用的确定权重的方式主要分为两类［9］：主观法和客观法。本文采用粒子群优化算法来确定评价指标的权重，以选定方案与最优和最劣对象之间的间隔之和最小为标准，创建一个建立在权重上的非线性规划模型，将各评价指标的重要程度客观得体现出来。

1 粒子群优化算法

1995年James Kennedy和Russell Eberhart最早提出了粒子群优化算法（Particle Swarm Optimization，PSO）［10］。PSO是经过对大自然中鸟群找食物的移动方式的研究模拟提出来的计算方法，选用了对于种群的整体搜寻战术以及单一的移动效率—位移形式。正因为PSO计算方法相当轻易并且具备其余的遗传计算法无法比拟的长处，获得了国际上很多科学家的注意。近年来粒子群优化算法的应用领域越来越广泛，整数规划、非线性规划、多目标优化、旅行商问题等领域都有使用该算法解决复杂问题的例子［11-13］。以选定方案与最优的目标和最劣的目标之间间隔之和最短为标准，重新定义权重的求取方式，做出非线性规划模型，运用粒子群算法来解答出评估目标的权重。

设有m个参评方案，每个方案有n个评价指标，这样就构成了一个m×n阶的矩阵Xm×n，以与最优的目标和最劣的目标间隔之和最短为标准来算定目标的权重。

若假设最优对象为 G＝［1，1，…，1］T，那么最劣对象为 H=［0，0，…，0］T，则目标如下：

式中：m为评价对象个数；n为评价指标个数。

首先采用罚函数法将优化函数（1）转化为如下的适应度函数，以便后期利用粒子群方法求解指标权重 ωj。

式中：A与B为惩罚因子。

2 权重设计

步骤1：粒子群的第i个体初始值为

式中：i=1，2，…，N，N 为粒子群的规模；j=1，2，…，n，n为个体粒子的维数。

步骤2：设置粒子群的惯性权值ω。

采用惯性权值动态变化的方法，将提高粒子群的全局寻优能力提高。惯性权重ω的变化规律为

式中：ωmax为惯性初始权重；ωmin为惯性最终权重；kmax为粒子群算法的最大迭代次数；k为目前的迭代次数。 本文选取 ωmax=1.4，ωmin=0.8，kmax=1 000。

步骤3：设置加速度常数。本文选取c1=1.8，c2=1.8。

步骤4：评估粒子群单体的初始适应值，而且凭此设立个体史上最优pid和全体史上最优pg。

步骤5：进行迭代计算。

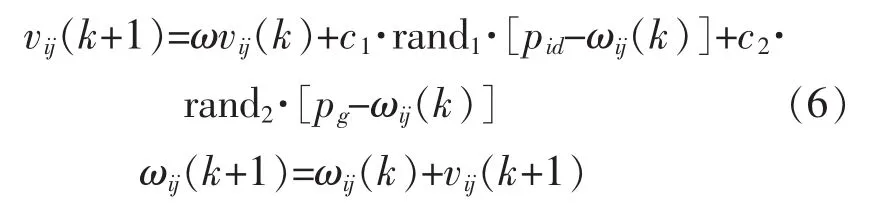
根据式（2）在每一次结束迭代计算后，评估粒子的适应值。根据式（7）～（8）保留全体史上最佳适应值所对应的粒子。

3 TOPSIS法原理

标准 TOPSIS是 Hwang和 Yoon［14］提出的一种多准则决策方法。经典的TOPSIS法是一种复杂的最小二乘法，常涉及复杂的算法步骤，难以学习和应用。在实际的多准则决策问题中，属性值往往是用不完全信息来表示的，但决策者可能更倾向于采用一种简单易用的方法，给出相同的结果而不是复杂的算法。提出一种新的简化TOPSIS方法，既简化计算，又得到与传统TOPSIS方法相同的结果。

TOPSIS法借用多属性问题中的理想解和负理想解给方案集X中的各个方案实行排列。理想解x*是一个计划集X中其实不存在的伪造的最好计划，其每一个属性值均为决策矩阵之中它的属性的最佳值；而负理想解x0便是假设的最差计划，其每一个属性值均为决策矩阵中它的属性的最差值。

TOPSIS法的详细算法步骤如下。

步骤1：求取规范决策矩阵。

采用用向量规范化的方法，设多属性决策问题的决策矩阵 Y=｛yij｝，规范化决策矩阵 Z=｛zij｝，则

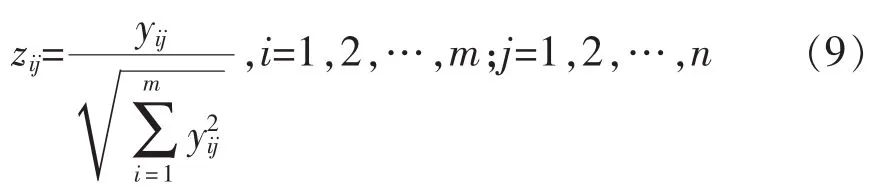
步骤 2：构成加权规范阵 X=｛xij｝。

设由决策人给定 ω=（ω1，ω2，…，ωn）T，则

步骤3：确定理想解x*和负理想解x0。

假设理想解为x*，则它的第j个属性值是x*j；负理想解为 x0，则它的第 j个属性值是 x0j，那么理想解：

负理想解：

步骤4：计算各个方案与理想解和负理想解之间的距离。

备选方案xi到理想解的距离为

备选方案到负理想解的距离为

步骤5：计算各方案的综合评价指数。

4 改进TOPSIS法在火电厂混煤掺烧中的应用

4.1 混煤掺烧评价指标体系设计

6个性能指标中的成本型指标包括灰分、着火温度、价格；效益型指标为挥发分、发热量和灰熔点。

表1 8种混煤配比方案的性能指标

灰分无益于氧元素和可燃质的混合反应，煤粉引火速率与燃烧温度均会下降，高灰分煤烧火稳定性与可燃尽度相当低，受热一面的损失加重，制粉体系的电量消耗上升。挥发分是指当煤被加热到相对应的温度之后，煤中的部分矿物质与有机物产生化学反应离解之后散发出的气体［15］。适当的挥发分有助于煤的燃烧，但过高则会影响到制粉机制的平稳运转，极其容易烧坏燃烧器的喷口，并且未完全烧完的产物炭粒，会进一步生成更多的污染物，不完全燃烧会导致煤炭的燃烧效率显著下降。挥发分含量过低则会使煤粉点火艰难，锅炉燃烧亦不稳定，乃至会有熄火事故发生［16］。

4.2 应用

利用 TOPSIS法，m=8，n=6；由表 1可得，决策矩阵如下：

将上述矩阵进行归一化处理，得到属性矩阵如下：

由粒子群优化算法计算出各指标权重为：ωj=（0.167 0，0.153 7，0.170 1，0.169 5，0.169 8，0.169 8）

则加权的标准化属性矩阵如下：

由矩阵 V 和式（11）和式（12）得：

正理想解集合为 V+=（0.075 1，0.025 9，0.055 6，0.066 5，0.055 8，0.063 9）

负理想解集合为 V-=（0.042 6，0.099 5，0.064 8，0.052 9，0.065 4，0.057 1）

各自用式（13）和式（14）求各个方式到理想解的间距和负理想解的间距如下：

S+=（0.725 8，0.683 4，0.747 6，0.846 8，0.781 6，0.721 4，0.757 1，0.825 0）

S-=（0.728 8，0.687 2，0.752 8，0.851 4，0.786 8，0.726 4，0.756 0，0.830 8）

混煤配比计划的指标值和理想解之间相对的接近比例：

Ci＝（0.50103，0.50137，0.50173，0.50135，0.50166，0.501 73，0.499 64，0.501 75）

比较Ci的大小可得方案8最好，方案7最差。

5 结语

将粒子群优化算法和TOPSIS法相结合，构建了火电厂混煤掺烧方案选择模型，在求取各项指标对象的权重的过程中加入了粒子群优化算法。这种求取权重的方法拥有严谨的逻辑性，防止评价指标权重确定的主观性，使确定的权重更符合客观实际，实例考证了这种方法的有效性与合理性。提出的基于粒子群优化算法定权的TOPSIS法可适用于评估属性繁多、决策者鉴别不准的问题，而且此方法看起来直接简便，更方便在计算机上达成其功能。