2K-H行星齿轮传动优化设计数学建模与解算

史素华

（山东省民族中等专业学校，山东 潍坊 262500）

渐开线行星齿轮传动与普通定轴齿轮传动相比具有承载能力大、体积小、效率高、重量轻、传动比大、噪音小、可靠性高、寿命长、便于维修等优点，广泛应用于小汽车、重型载重汽车、工程车辆和飞机等的传动系中[1]。

研究指出，同一制造精度下，行星传动比起定轴线固定传动，载荷一般沿齿宽分布得较好[2]。这是由于在行星传动中齿宽对直径的比值一般不超过0.7，而在普通减速器中却达到1.6，在个别情况下，例如在涡轮机减速器中则显著超过此值。在同样条件下，行星传动的箱体重量比普通定轴齿轮传动的箱体其重量要小好几倍，因为行星传动箱体外廓尺寸比普通定轴齿轮传动的箱体要小得多。

设计行星传动时，正确选择齿轮参数的意义远比设计普通定轴传动的大。齿轮参数选择不当时，不但可能丧失在外廓尺寸和重量方面的优点，甚至可能得到不利于使用的传动。

按最小体积为目标对行星齿轮机构进行最优化设计，不仅对缩小体积，而且对减小质量、节约材料及降低成本等都是很有实效的，这些对汽车及飞机这一类的产品尤其重要[3]。现在就以这类产品中常采用的2K-H型行星齿轮机构作优化设计。

一、2K-H行星齿轮设计要求

对于2K-H行星齿轮，如右图所示，要设计一个符合条件的行星齿轮传动，需要根据已知条件确定齿轮的几个参数：各齿轮的齿数z，模数m，齿宽b，如果将行星轮的个数也作为设计变量，则有四个参数。根据机械设计知识，行星齿轮参数需要满足以下两种条件：一是几何设计条件就是在不考虑材料视齿轮为刚体的情况下齿轮正常传动的条件；二是齿轮的强度条件，行星齿轮作为一种机械构件，需要在确定材料的情况下对强度作一定的要求，保证齿轮到达预期寿命[4]。以下作具体分析。

（一）行星齿轮传动几何设计条件

根据机械设计知识，在行星轮系中，各轮齿数的选配需满足以下四个条件。

1.传动比条件。保证实现给定的传动比。

2.保证两中心轮及系杆的轴线重合，即要满足同轴条件（同心条件）。

当采用标准传动和等移距变位传动时，可得

3.保证各行星轮能够均匀地装入两中心轮之间，即要满足装配条件（正确配齿）。

q—行星轮数，C—正整数

4.保证各行星轮不互相碰撞，即要满足邻接条件。

要保证相邻两行星轮的齿顶互不相碰，相邻两行星轮的中心距应大于行星轮齿顶圆直径。

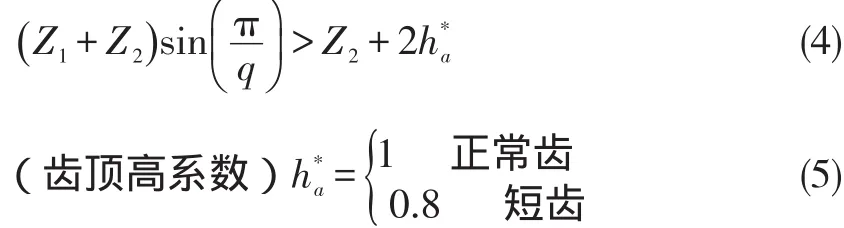
（二）行星齿轮传动强度设计

1.齿面接触疲劳强度条件

校核公式为

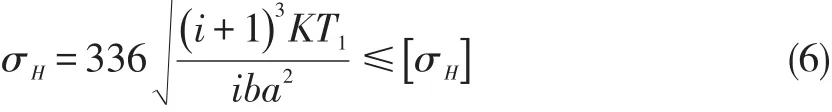
式中

K—载荷系数

T1—齿轮1转矩（N∙mm）

P—传递功率（kw）

n1—齿轮1转速（r/min）

b—计算齿宽（mm）

m—齿轮模数（mm）

[σH]--许用接触应力（MPa）

整理得

2.齿根弯曲疲劳强度条件

校核公式为

YF—齿形系数

[σF]—许用弯曲应力（MPa）

化简得

（三）其他设计条件

1.不根切条件

2.齿宽限制条件

二、建立优化数学模型

（一）确定设计变量

取中心轮1齿数Z1、模数m、齿宽b和行星轮个数q为设计变量，即

（二）确定优化目标函数

按最小自重进行优化设计，取中心轮1和行星轮体积之和作为行星齿轮传动重量指标。则目标函数可表示如下：

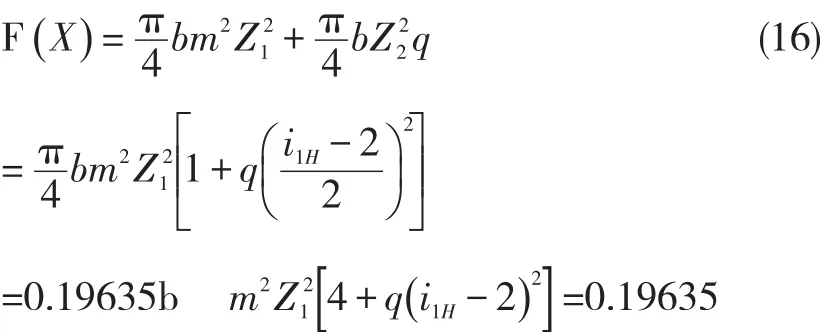
（三）确定约束条件

1.几何约束

2.强度约束

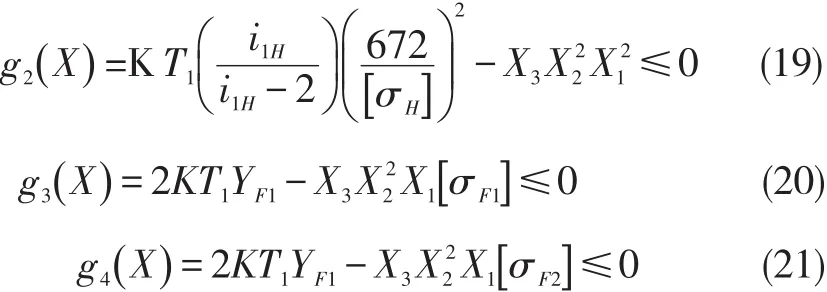
（四）其他约束条件

（五）建立优化数学模型

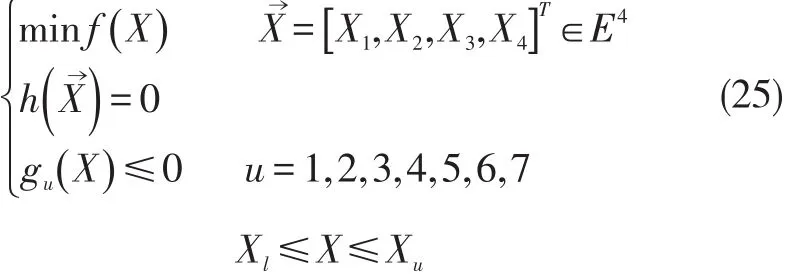
Xl、Xu分别为设计变量X→的上、下界向量。

三、行星齿轮机构的最优化求解

由上面的分析可知，要对行星齿轮机构进行最优化求解，就是求解一个四维约束问题，同时考虑到一些变量为整形。所以归纳起来，2K-H型行星齿轮机构的最优化过程分为两个阶段：第一步是将设计变量看成是连续变量对目标函数求解最小值，第二步是对所求得的最小值的各个实型分量（参数）进行圆整和标准化处理。由上得出最优化的设计参数。

对于数学模型的求解，采用约束变尺度法，利用Fortran语言进行编程解算。

四、设计实例

某行星齿轮传动，已知传递功率P=4.78MW，传动比i1H=3.45，输出转速nH=487r min，齿轮材料强度 分 别 为[σH]=960MPa，[σF2]=378MPa，[σF1]=310MPa。

根据已知条件，带入已建成的数学模型，对于YF的值，将曲线离散成24个点运用插值算法来取值。

除此之外，限制设计变量的上下限：

经上面的求解，得到以下结果：

Z1=73,Z2=53,Z3=179,B=56mm,m=3.75mm,q=7

五、结论

以上为数学建模的过程及设计实例，由此可以看出建立的数学模型行星齿轮传动的最优化问题得到了解决，设计实例中算出的结果与实际数据相符合。