基于全球定位系统测速的城市轨道交通列车运行阻力研究

张 皓 刘 杰 周和超

(同济大学铁道与城市轨道交通研究院，201804，上海//第一作者，硕士研究生)

城市轨道交通列车的运行阻力特性直接关系着运行能耗以及列车自身进一步的优化和设备改进，对于运行图的制定也具有参考意义。文献[1]利用目前运行阻力试验的主要方法——测算惰行时的车轮转速，计算出车辆惰行的速度，从而得到相关的数据进行单位基本运行阻力的求取。这种方法存在较大的误差：在车轮上安装的传感器与车轮圆心不能完全重合会带来误差，轮径不一致也会产生误差，且设备安装较复杂。与上述方法相比，利用GPS(全球定位系统)测试方法获取相关数据，误差小且设备易于安装。GPS测速方法虽然具有较高的准确性,但仍然存在一些可能的误差。为此，本文对列车进行基于GPS测速的运行阻力试验，并与同类型列车对比分析，以评价该列车的运行阻力特性。

1 试验概况

1.1 试验条件

试验在指定的线路上进行。试验线路平直且无坡道，总长为1.6 km，并在试验前已完成线路的安全检查。试验在气候干燥且天气状况良好的条件下进行[2-3]。试验列车为4拖2动6节编组的地铁车辆，试验时的载荷为AW0(空载)工况。按照测试标准要求，该列车的运行速度范围为0～79 km/h。列车相关参数见表1。

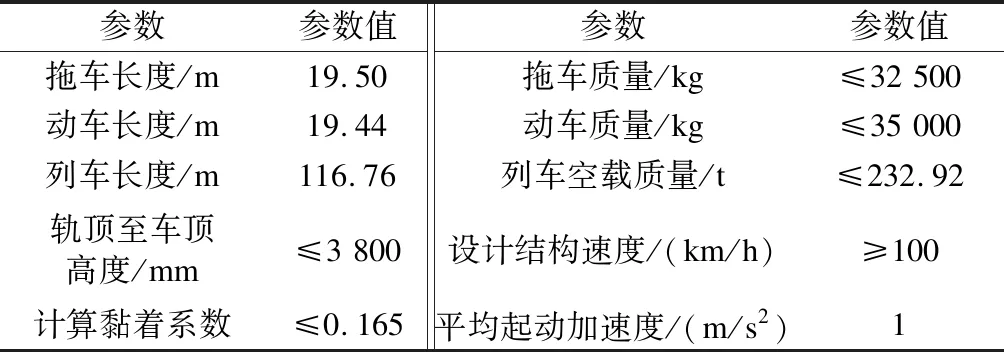
表1 试验列车相关参数

1.2 试验过程

1.2.1 试验方法

按照速度表的要求，试验列车速度提高至大于等于规定的惰行开始速度v0，第一次试验的惰行开始速度为10 km/h，下一次试验的惰行开始速度在上一次试验的基础上提高5 km/h，以此类推，直至达到最高的惰行开始速度79 km/h。在提速过程开始时记录数据，速度达到要求后，车辆开始惰行，惰行区间总长400 m；驶出惰行区间之后，以常用制动的方式使列车制动到速度为0，此时停止记录数据。司机室换钥匙，原先的车尾成为车头，按照上述反向重复操作2次并记录数据，即每个不同的惰行开始速度需要按照要求进行3次完整的试验，记录3组数据。

利用基于LABVIEW软件编写的测试软件实时记录GPS测速装置获得的初始速度数据，并用软件拓展的计算功能通过积分导出位移曲线。用采样分析的方法(采样频率为10 Hz)和回归算法对数据进行计算：利用采样点回归计算出速度变化曲线，得出曲线变化率特征，从而计算出该点处加速度及阻力的大小；利用回归算法数字特征评价计算结果。在计算时主要以MATLAB软件为计算工具。

1.2.2 数据采集

数据来自GPS测速仪。选用的GPS测速仪型号为HR-GPS-10(RL)GPS，经过专用的信号调制器和测试软件实时地记录于计算机中。文件以函数图像的形式保存，并可以转换成数据表格的形式。

2 试验数据分析

2.1 试验数据处理方法

根据试验方法计算出试验列车惰行时的加速度ai，再将加速度数据转化为单位基本运行阻力ω0i[4]。每一组ai、ω0i所对应的横坐标vi为该组速度值的中位数。

(1)

ωi=i

(2)

ωr=600/R

(3)

式中：

γ——回转质量系数，取为0.11；

ωi——单位坡道附加阻力,N/kN；

ωr——单位曲线附加阻力,N/kN；

i——坡道坡度，上坡时取正值，下坡时取负值；

R——线路圆曲线半径，m。

在平直无坡道线路的试验条件下，i和R均为0，故ωi和ωr也为0。

利用这一系列的数据绘制出以速度为自变量、单位基本运行阻力为因变量的函数图像；再次利用最小二乘法归纳出单位基本运行阻力随速度变化的阻力公式。

2.2 试验数据分析

按照上述方法对试验所得的数据进行分析，先后得到各速度值对应的惰行加速度和单位运行阻力，其部分结果如表2所示。

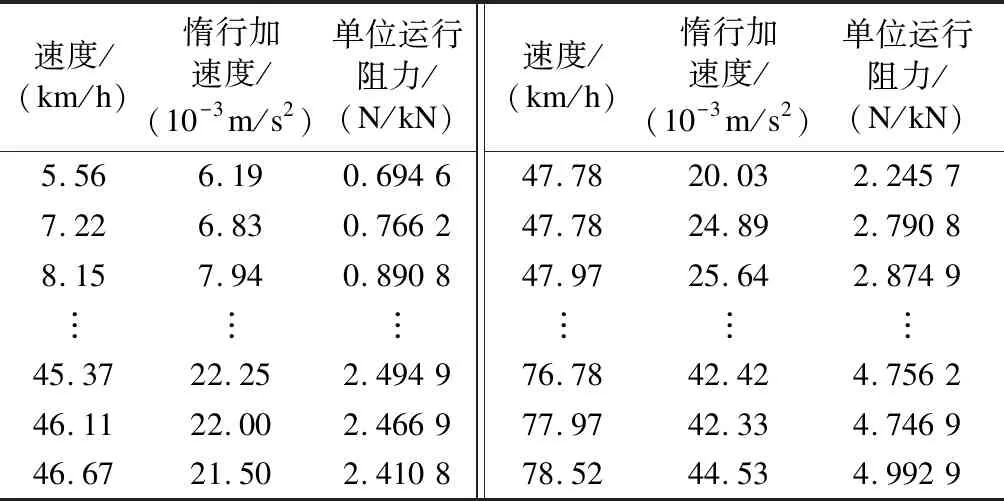
表2 列车试验数据分析

根据求得的全部数据，绘出对应的散点图。基于该散点图，利用最小二乘法拟合出所对应的单位基本运行阻力曲线，并归纳出对应的单位基本运行阻力公式，见式(4)。散点图与基本运行阻力曲线如图1所示。

ω0=0.570 4+0.022 66v+0.000 412v2

(4)

式中：

v——列车运行速度，km/h。

图1 列车速度-运行阻力曲线

2.3 有效性验证

为了验证式(4)的有效性，利用该式和列车相关参数计算出某工况列车的理论能耗值，然后将计算结果与实际能耗值相对比，从而对式(4)的有效性进行初步验证。

根据能耗测试，该列车从30 km/h加速到79 km/h共消耗14.90 kW·h的能量。地铁列车电气功率可用下式来计算：

P=Fv/η=(f1+ma)v/η

(5)

式中：

P——需要求取的电气功率；

F——轮周牵引力；

v——列车运行速度；

η——列车牵引系统总效率；

f1——列车的合成阻力(包括基本运行阻力f0、曲线、坡道等附加阻力)；

m——列车总质量(包括回转质量)；

a——列车运行时的加速度。

对式(5)积分，得出某区间内列车消耗的总能量表达式：

E=(f0S+mgΔh+0.5m0v2)/η

(6)

式中：

E——需要求取的总能耗，kW·h；

S——列车行驶距离，m；

Δh——列车高度增量(此处为0)；

m0——列车静态质量，kg。

对于同类型的4拖2动上海轨道交通11号线列车，文献[5]通过仿真和试验发现，当列车速度>30 km/h时η保持在80%～90%之间。为了方便η的取值，选择该列车从30 km/h加速到79 km/h的工况进行计算，此处η取0.85。由1.1试验条件可知，该列车牵引加速度为1 m/s2，则v=t+8.33，S=0.5t2，f0=m0ω0，而t的变化范围为[0,13.61]，故可用下式计算总能耗：

(7)

式中：

ω0——列车单位基本运行阻力；

t——列车加速过程的时间，s；

vmax——列车加速过程中的最大速度，m/s；

vmin——列车加速过程中的最小速度，m/s。

将式(7)代入数值，求得总能耗为14.47 kW·h，与实际消耗的能量相当，故可知利用该单位基本运行阻力公式推算列车能耗的结果正确，因而从能耗角度验证了GPS测试方法的有效性。

2.4 误差分析

试验结果的误差来源主要有两个：一是数据处理方法产生的误差，二是试验数据测量误差。

首先对回归分析的结果进行评价，列出归纳公式(4)的拟合优度(Goodness of fit)[7]。相关参数如下：离差平方和(SSE)为6.623；确定系数(R-square)为0.952 5；均方根误差(RMSE)为0.293 3；置信度R2=0.974 1。可以认为，以最小二乘法为基础的数据处理方法所产生的误差小，拟合优度高。综上可知，试验推导出的单位运行基本阻力公式准确。

相比于通过测量车轮转速来推算记录列车速度的传统方法，利用GPS测速方法有效克服了传感器无法准确定位车轮正中心所产生的误差，以及轮径不一致带来的误差。尽管所选用的GPS测速仪器在精度上可靠[6]，但误差依然存在，误差来源可以概括为以下3个：

(1)GPS测速仪受到卫星信号强度变化的影响，少量数据失真，影响结果准确性；

(2)尽管在列车各节车厢中多处布点取均值，但列车的纵向振动仍会带来误差；

(3)在试验前对于GPS设备进行了时间调零，但随着试验推移，设备间可能存在较小的不同步现象。

3 试验结果对比

为了方便进一步评价该列车的运行阻力特性，将试验结果与近几年同类型列车的运行阻力特性进行对比。选取的比较对象为同类型的广州地铁5号线列车[1]和杭州地铁1号线列车[8]。

广州地铁5号线列车的单位基本运行阻力计算公式为[1]：

ω0α=0.954 2+0.004 734v+

0.000 7436v2

(8)

杭州地铁1号线列车的单位基本运行阻力计算公式为[8]：

ω0β=0.737 7+0.022 66v+

0.000 859 9v2

(9)

从图2可以看出，无论是车辆运行在低速还是高速，本试验列车的单位基本运行阻力在数值上都要比另外两个小，在高速运行的情况下，差距更为明显。从变化率的角度来看，本试验列车阻力值的变化更为平缓，对列车牵引系统的冲击更小。综合以上两点，本试验列车表现出良好的运行特性。

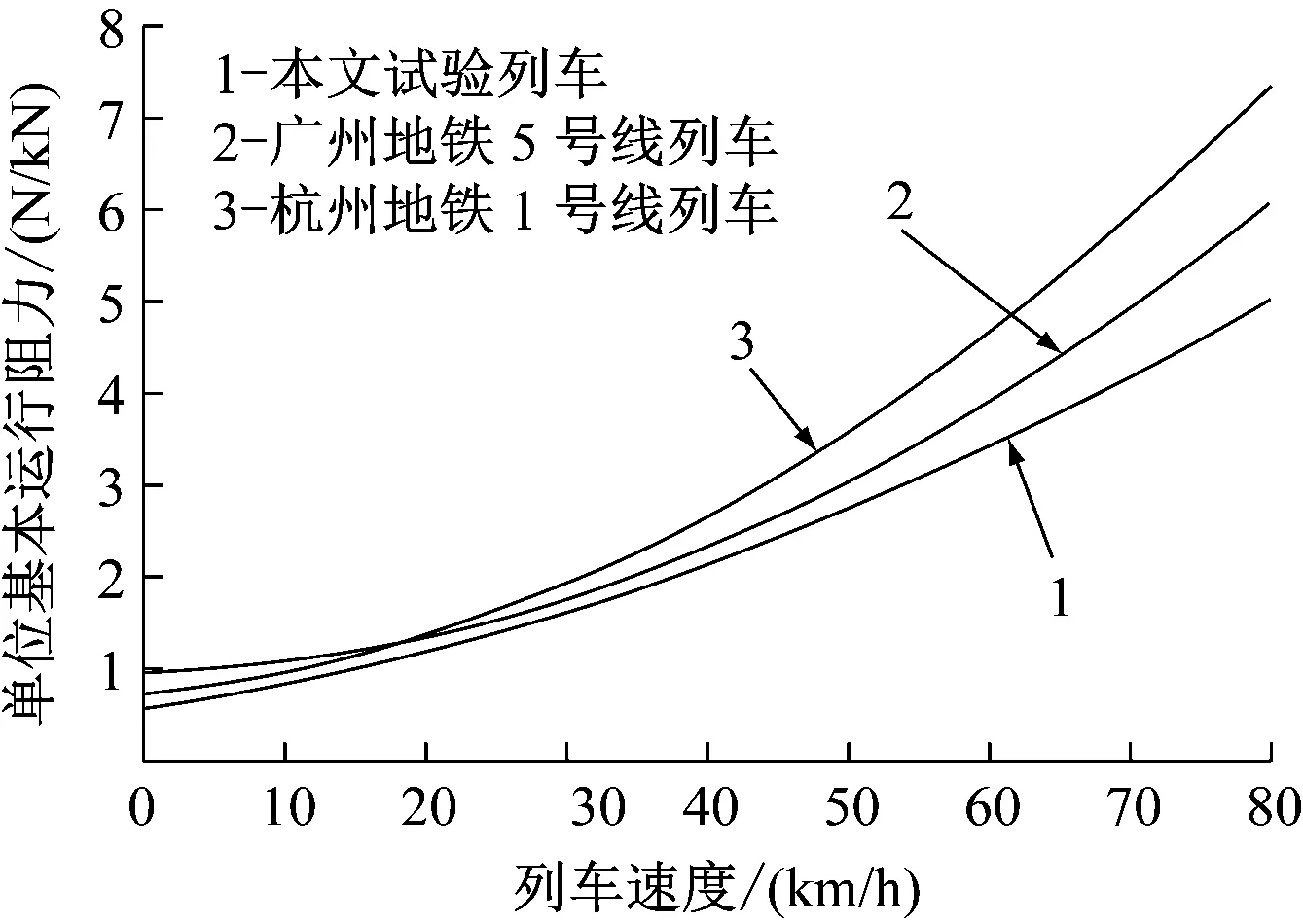
图2 三城市列车的单位基本运行阻力比较图

4 结论

(1)通过误差分析与能耗计算，验证了GPS测速方法用于列车运行阻力测定的有效性。利用成熟的统计学方法，更为精确地得出了列车的单位基本运行阻力公式；同时，利用多个测速装置同时测速、取均值的做法，有效减小了列车运行时纵向振动所带来的测量误差。但该误差并未完全消除。如何方便有效地消除该误差仍然需要作进一步探索。总体上，利用GPS测速方法使得测算准确，同时也减小了试验的工作量。

(2)通过对比分析某城市轨道交通列车与同类型其他列车的运行阻力特性，发现被测列车的单位基本运行阻力较同类列车小，运行阻力随速度的变化也较为平缓，故该列车表现出良好的运行特性，能够有效降低能耗，便于牵引动力基本参数的选择与配置。