车用轴流风机离散噪声与叶片分布特性研究

钟银辉 李以农,2 高 峰

1.重庆大学汽车工程学院，重庆，4000442.重庆大学机械传动国家重点实验室，重庆，400044

0 引言

车用风机作为冷却系统的核心部件，其工作噪声对整车噪声影响很大，特别是风冷发动机，其工作噪声往往是主要的噪声源之一。汽车的电动化消除了传统发动机噪声的掩蔽作用，使得车用风机在某些工况下的“嗡嗡声”及高频噪声显得尤为突出，极大地影响了车辆的乘坐舒适性。

为了获得大的空气流量，现代汽车普遍采用轴流式冷却风机。风机正常运行时，叶片产生的气动噪声远远大于风机的机械噪声和电磁噪声[1]。轴流风机气动噪声通常可分为离散噪声和宽频噪声两种。在风机叶片等间距分布时，叶片尾迹气流周期性地冲击下游物体形成的声压脉动叠加在叶片脉动基频及其谐频上，使得离散噪声的声压级远高于宽频噪声的声压级[2]。目前，许多学者都是通过改变叶片分布特性来降低离散噪声的，其中不同数量叶片和非等间距分布方法因具有结构紧凑等优点而备受重视。

针对叶片数量方面的研究，张红辉[3]从理论上得出了风机叶片数量与声功率的正比关系；张立等[4]利用数值模拟和实验的方法证实改变叶片数量能够降低风机噪声；张代胜等[5]通过仿真得出流量、总声压级与叶片数量的关系，指出在满足流量情况下，合适的叶片数量能较好地降低噪声。以上研究均未涉及风机的离散噪声均未涉及。

针对叶片非等间距分布方面的研究，根据Lighthill的气动声学理论，WRIGHT等从不同角度导出了等间距叶片的声辐射公式[1]；孙晓峰[6]在WRIGHT的基础上，推出了不等间距叶片噪声的声辐射公式，成功预测出某不等间距叶片与等间距叶片在叶片通过频率处噪声比的降低幅值；伍先俊等[7]通过设计不等距叶片的措施将基频处的噪声峰值分散到其他频率上，从而降低了离散噪声；LEE等[8]采用多方案进行了叶片的不等间距设计，并进行了数值仿真及实验验证，指出采用合适的非等间距方案可以较好地降低离散噪声；马健峰等[9]根据叶片自平衡的分配方案进行叶片的不等距设计、数值模拟及实验研究，证明采用不等距叶片可以减小离心通风机基频噪声的峰值，但总的噪声级基本不变；刘志超等[10]通过仿真分析指出，非等距叶片分布能使旋涡自吸泵的脉动主频和幅值发生变化；汤黎明等[11]指出叶片不等距分布方案可获得最大的流量和较低的噪声值；张代胜等[5]、耿丽珍等[12]根据叶片自平衡的分配方案进行叶片的不等间距设计及数值仿真，得出流量、总声压级与非等间距分布特性之间的关系，指出在满足流量情况下，非等间距分布能较好地降低噪声。以上均是通过举例来说明某非等间距分布方案对降低离散噪声有效果,但没有提出最优降噪效果的非等间距分布方法。本文通过研究不同数量叶片和非等间距的分布特性来降低离散噪声。

1 风机离散噪声相关理论

离散噪声是离散频率噪声，源自叶片形成的空气压力脉动。风机旋转时，每个叶片的两侧由于流速不同而产生压力差，因此形成的流场以风机旋转速度旋转，使得流场中任一点的压力都发生周期性的变化。

叶片等间距分布的风机离散噪声频率

(1)

式中，n为谐波数，当n=1时，f为风机离散噪声基频，即第1阶脉动噪声频率；B为风机叶片数；N为风机转速，r/min。

(2)

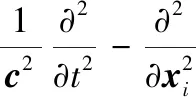
取控制面f(xi,t)=0为扇叶面，由无穿透条件un=vn可得FW-H方程最常用的一种形式：

(3)

其中，Fi为叶片表面负荷分量；等号右边3项分别代表厚度声源、载荷声源和四极子声源。厚度声源和载荷声源是面声源(由Dirac函数决定)，取决于叶片表面的形状、运动速度以及非定常气动力，在低速和亚音速流动中，面声源贡献占总的气动贡献的绝大部分；四极子声源是体声源(由Heaviside函数决定)，它与控制面附近的非线性流动密切相关，当控制面附近达到跨音速或超音速时，四极子噪声尤为突出。

因车用轴流风机处于低速和亚音速流动中，故四极子噪声可以忽略。假设体积密度为常数，进入到流体中的非平衡质量流相当于一个单极子，故厚度声源可以忽略，此时，FW-H方程可表示为

(4)

对于叶片转子，外力Fi应是气流与叶片的相互作用力，用其相互作用的压力场来表示。

如果叶片与气流的相互作用力呈现周期性，则可以将作用力展开成傅里叶级数，但对于非等间距叶片，它与气流的相互作用不作周期为2π/B的周期性变化，因而不能直接展开，本文从谐波法角度导出作用力表达式。任意一个叶片转子与来流相互作用的脉动压力场可表示为[6]

(5)

图1 风扇相关参数示意图Fig.1 The sketch map of fan’s relevant parameters

一种常见的不等间距分布规律如下：[13]

φ＇=φ+Δθsin(mφ)

(6)

式中，Δθ为最大的两叶片夹角改变量，即单叶片的调制振幅，-π/B≤Δθ≤π/B；m为调制量的循环次数。

另外，θB=BΔθ为最大调整角，主要调整离散噪声峰值及其旁瓣对应的峰值。

由式(5)和式(6)可得该类不等间距叶片脉动压力场

(7)

由于转子以角速度ω旋转，所以压力场也是随时间变化的，即

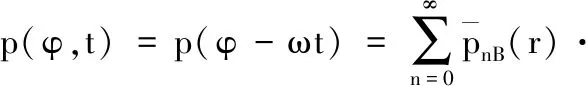
(8)

对任意一个谐波分量而言：

(9)

由于

(10)

(11)

式中，J0、J2n均属于第一类贝塞尔函数。

故式(9)可写为

(12)

所以任意一个子谐波的分量是：

Jv(nBΔθ)[cos((nB+vm)(φ-ωt)+φ0)+
(-1)vcos((nB-vm)(φ-ωt)+φ0)]

如图1所示，任意一个子谐波辐射到观察点x1的声压为[6]

(13)

ξF=FnB(cosγcosθ)

(14)

(15)

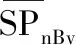
任意一个谐波的声辐射应是各个子谐波的叠加，即

(16)

式(16)即为非等间距叶片分布在稳定旋转力作用下的声辐射公式。在式(16)中，有

ΗnB=nBJnB(nBMasinθ)

(17)

ΗnB±vm=(nB±vm)JnB±vm[(nB±vm)Masinθ]

(18)

当Δθ=0时，即叶片等间距时，贝塞尔函数J0(nBΔθ)=1,Jv(nBΔθ)=0(v>0),则有

(19)

将式(14)、式(15)、式(17)、式(18)代入式(19)可得

(20)

在风机轴线上布置一个麦克风，则θ=0°，nBMasinθ=0，JnB(nBMasinθ)=JnB(0)。只有当n=0时，JnB(0)=1，其余状态下JnB(0)=0，故式(20)可写为

(21)

(22)

(23)

(24)

将式(21)～式(23)代入式(24)可得

(25)

通过仿真可得到风扇的转矩T、沿轴向e3的作用力F、叶片在每个单元对应的垂直于叶片的作用力FnB、作用力FnB与e3之间的夹角γ，由此可得出风机的声压级公式。

2 非等间距叶片优化方法

对于任意一个谐波，不等间距叶片分布不像等间距那样对应着明显的峰值，而是由许多对应于振幅为J0(nBΔθ)(ξT-ξF)ΗnB的频带组成的，即不等间距叶片分布使频率发生了调制。

(26)

基于式(26)可得相对于等间距叶片任意一个谐波下降的声压级：

(27)

由第一类贝塞尔函数得

(28)

将θB=BΔθ代入式(27)及式(28)，同时取n=1，可得第1阶脉动谐波噪声减小量ΔS与最大调整角θB之间的关系：

(29)

为了确定θB的范围，以工程常用的9叶片为例，根据式(6)进行非等间距分布，如图2所示。由图2可知，θB为2.7 rad时叶片之间有间隙；θB为π rad时，叶片间隙为0，处于临界点；θB为3.6 rad时，叶根附近出现了明显的叶片重合现象，故将θB设定在-π～π rad范围内。

(a)θB=2.7 rad (b)θB=π rad(c)θB=3.6 rad图2 不同最大调整角θB对应的非等间距分布Fig.2 Unequal interval distributions corresponding to different maximum adjustment anglesθB

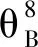
(30)

为了得到该方程的极值点，对式(30)求导后设为0，可得θB取实数-2.406 rad、2.406 rad，图3所示均为最大值，由于此函数为偶函数，故在此范围内存在唯一的正实数2.406 rad，使得第1阶脉动噪声降幅最大。

图3 噪声峰值减小量与最大调整角之间的关系Fig.3 The relation between the decrease of sound pressure levels and the max adjustment angle

为了验证θB=2.406 rad时ΔS是否为最大值，采用仿真模拟及实验的方式进行分析验证。本文车用轴流风机以工程常用9叶片、转速2 400 r/min为例进行仿真模拟。由式(1)得，第1阶脉动噪声频率为360 Hz。最大调整角θB分别取0、0.9 rad、1.8 rad、2.406 rad、2.7 rad、π rad,其中,θB为0.9 rad、1.8 rad、2.406 rad、2.7 rad、π rad时均是非等间距方案, 为了与等间距方案的效果作对比,将θB=0的等间距方案也考虑在内进行分析。

将最大调整角θB=2.406 rad及对应的单叶片调制角Δθ=0.267 rad代入式(6)，分别以等间距叶片位置φ=40°，80°，120°，160°，200°，240°，280°，320°，360°作为基本条件，可得表1所示的数据。由表1可知，在θB=2.406 rad时，非等间距叶片相对于等间距叶片变化值不超过26.2%。按表1中θB=2.406 rad对应的相关参数进行叶片分布设计，即可得到9叶片的最佳非等间距分布方案。针对其余非等间距方案，可参照表1得出相应的几何模型进行仿真模拟。

3 仿真与实验分析验证

针对不同数量叶片，本文基于离散噪声理论采用仿真优化的方法获取叶片数量与噪声、流量、效率之间的变化规律，并通过实验验证；针对非等间距叶片分布中，θB=2.406 rad为最优降噪的方案，通过仿真与实验验证其效果，同时分析其对流量和效率的影响。

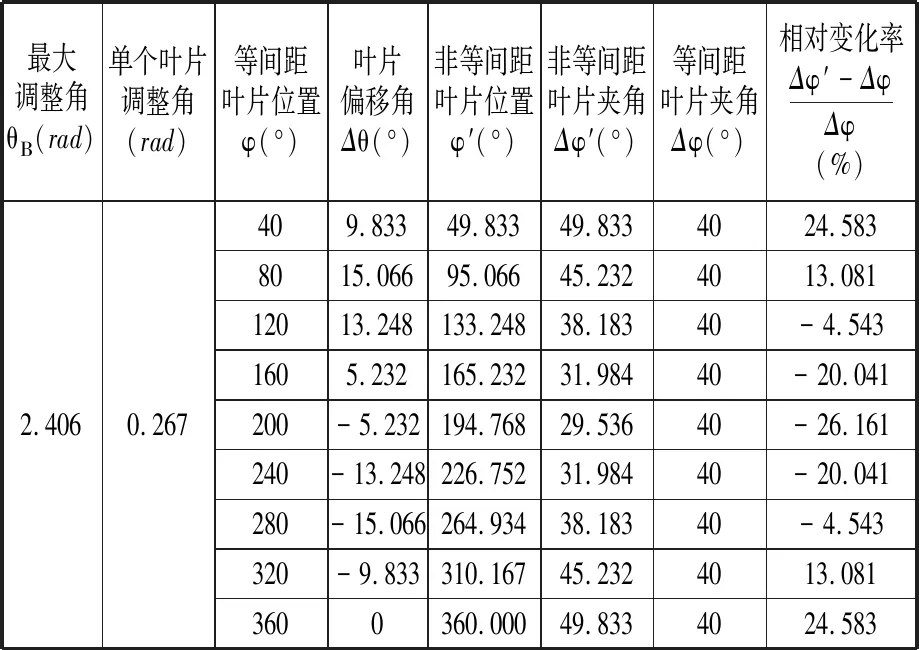
表1 非等间距叶片相关参数

风机的流量qv是指通过计算域进口或出口边界面空气的体积流量。

轴流风机的全压是出口全压与进口全压之差，具体可表示为

(31)

式中，p1为叶轮进口全压；p2为叶轮出口全压；pst1为叶轮进口静压；v1为叶轮进口流速；pst2为叶轮出口静压；v2为叶轮出口流速。

风机扭矩T由作用于叶轮表面各单元的正压力与剪切力形成的力矩累加得到，本次计算统计了作用在轮毂、叶片以及外边缘的力矩。

全压效率η可表示为

(32)

式中，nw为风机在稳态运行下的转速。

3.1 仿真

本文采用FLUENT软件进行仿真分析。

3.1.1仿真模型的建立

由于风机原模型比较复杂，所以在导入FLUENT软件前，要将一些对风机流场和声场影响较小的曲面去掉，以此来降低对计算机硬件的要求和节约计算时间，简化之后的风机三维模型见图4。其余不同叶片数量及非等间距方案的风机均基于此模型进行相应的改变，然后进行仿真分析。

图4 风机简化模型Fig.4 Fan model simplified

基于实物简化的风机仿真模型共分为进口域、出口域、动域和静域4个部分。图5为沿着X向(轴向)剖开的YZ网格的局部平面图，从中可以看出：风机作为动域置于管道静域中，风机直径为409 mm，轮毂比为0.4。整体计算域为圆柱形管道，管道直径为2 200 mm，X向为流动方向，进口域X向长度为1 650 mm，出口域X向长度为6 050 mm，静域X向长度为1 160 mm，管道X向总长度为8 860 mm。图6为动静域网格局部放大图，从中可以看出：动域包含叶片、轮毂以及与静域的连接面，静域包含轴对称的护风罩、与动域的连接面、与进口域以及与出口域的连接面。转子中心为坐标原点，由于转子旋转部分的流体比较复杂，需要更加密集的网格来捕捉流场信息，故将动域单独划分为一个计算域。同理，将静域也单独划分为一个计算域。对风机的静域进行了不同程度的延伸，即形成了进出口域，这样就保证了来流和出流的均匀性，也保证了计算流场的稳定性。进出口区域对经过风机做功前后的流体进行模拟，各划分为一个计算域。

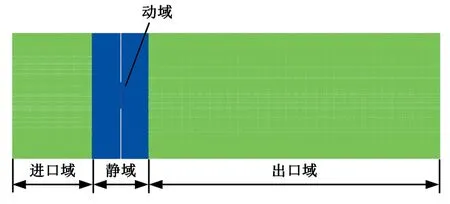
图5 计算域分布网格图Fig.5 The mesh sketch of computing region distribution

图6 动静域网格局部图Fig.6 Local sketch of rotating and static domain mesh

3.1.2网格划分

采用前处理软件ICEM对仿真对象进行网格划分。由于静域区和旋转区的结构比较复杂，用结构化网格不能满足不规则区域的网格要求，故采用非结构化网格。为了统一，进出口域也使用非结构化网格。在划分网格时，不同的计算目的对网格的要求也不同，所以，本文根据计算目的及流场处理的要求对模型进行网格划分。进口域和出口域采用规则拉伸的五面体棱柱网格，网格尺寸为28 mm；动域中的叶尖及前后缘处网格尺寸为0.3～0.8 mm，为了研究风机表面的流场及噪声特性，在固体表面增加5层边界层网格，主要为五面体棱柱网格，第一层网格尺寸控制在0.01 mm，其余位置为四面体网格，尺寸主要控制在6 mm。同时考虑实际情况，提高精度，在护风罩表面也增加5层的五面体棱柱网格用于流场及噪声计算，第1层网格尺寸控制在0.1 mm，其余为四面体网格，尺寸主要控制在24 mm。以上边界层网格均采用标准的固体边界处理方式，保证仿真结果的真实有效性，模型总网格数大约为935万。

3.1.3计算方法及初始边界条件的设定

在风机流道中流动的介质是空气，风机运动区域内的流体属于湍流运动，内部流体可认为是不可压缩气体，不考虑能量守恒方程，忽略重力对流场的影响。定常计算选取RNGk-ε湍流模型，压力-速度耦合采用压力耦合方程组的半隐式方法(SIMPLE)算法，选用非耦合隐式求解器。为了提高计算精度，控制方程的数值离散方法采用二阶精度迎风差分格式，迭代求解采用亚松弛因子。叶轮动域采用多重参考坐标系MRF，将动域的非定常流动视为定常流动，各项的收敛残差为10-5，以出口处的质量流量作为控制指标进行观察，初始进出口的相对压力均为0,速度为0,风机稳态转速为2 400 r/min。以定常计算收敛所得到的流场数据作为计算初场，基于压力的隐式二阶算法，采用大涡模拟(LES)的亚格子Smaqorinsky-Lilly模型重新计算流场。压力与速度耦合采用压力隐式分裂算子(PISO)算法，交界面设置在动域和静域的交界处，使用滑移网格。

在距风机中心背风1 m处布置一个噪声观测点进行仿真计算，噪声预测采用FLUENT软件中的FW-H声学模型来模拟，并用快速傅里叶变换(FFT)方法对噪声时域数据进行处理，获得噪声频谱特性。

3.1.4仿真结果的初步验证

为了保证仿真结果的有效性和准确性，从声压波动的时域数据及Yplus值两方面来进行初步的分析验证。

风机观测点处声压随时间的变化如图7所示。由图7可知，从第3个周期开始整个风机噪声观测点的声压波动处于一个较为稳定的状态，故对时域数据从第3个周期开始进行提取，每个点采样时间为0.000 1 s，每个周期为0.025 s，即250个时间步，取大约8个周期的稳定数据进行FFT变换，从而进行相应的频谱分析。

图7 风机观测点处声压随时间的变化曲线Fig.7 The graph of sound pressure varying with time at observation point

针对5层边界层网格，采用标准的固体表面方法进行边界层的近壁面处理。以4叶片(用于不同数量叶片的研究)为例，图8a所示的风机吸力面侧和图8b所示的风机压力面侧的Yplus值均在1左右，满足近壁面网格处理的要求，尤其叶片部分的Yplus值在0～1之间，保证了仿真的准确性，其余模型也满足Yplus值的要求。

(a)吸力面侧 (b)压力面侧图8 风机吸力面和压力面的Yplus值Fig.8 The Yplus value of suction side and pressure side of axial fan on the first model

3.2 实验方法

本次实验风机转速为2 400 r/min，结合仿真的其他输入条件，为仿真计算提供对比依据。

3.2.1风机流量实验

风机的流量实验采用MGS(metal gear solid)风机性能测试系统，通过控制风道阻力，可测试、获取不同全压下风机的流量，通过传感器采集数据并输入数据采集仪，经过A/D转换，将数据传入计算机。

3.2.2风机单体噪声实验

风机单体噪声实验如图9所示，将风机单体四角通过弹性绳固定在台架的上下横梁上，使得风机与台架隔开，保证了风机产生的振动不会通过弹性绳传至台架上，引起台架振动，产生噪声干扰。外接稳压电源，驱动风机在规定的转速下运行，采用LMS噪声振动测试设备，在距风机中心背风1 m处布置一个传声器作为观测点进行噪声实验。

图9 风机单体噪声实验Fig.9 Bracket experiment of single fan’s noise

3.3 仿真与实验结果分析

本文通过仿真得到了风机的流量、全压、扭矩等流场参数，进一步分析得出了流量与全压之间的关系，以及通过式(32)得出了全压效率与流量之间的关系；另外，基于稳态流场收敛的结果再进行瞬态流场仿真分析，获取声压时域数据，然后对其进行FFT分析，进一步得出离散噪声及相应的总声压级。基于仿真的相关条件及结果进行相应的实验验证。

3.3.1不同数量叶片对噪声、流量及效率的影响

在2 400 r/min稳态条件下对4叶片至11叶片等间距风机进行噪声、流量及效率的仿真计算，以7叶片和9叶片风机为主要对象进行实验验证。

为了分析离散噪声的特性，以9叶片为例进行仿真。通过对风机中心背风1 m处观测点的噪声时域数据进行FFT变换获得噪声频谱，结果如图10所示。由图10可知，9叶片表现出明显的离散噪声特性，第1阶脉动噪声峰值最大。从4叶片至11叶片离散噪声中提取第1阶脉动噪声进行分析，结果如图11所示。由图11可知，除了7叶片与11叶片,其余随着叶片数量增加，离散噪声也相应增大(从式(25)看，风机离散噪声幅值与叶片数存在正比关系，但受叶片的转矩、表面作用力等参数的影响，风机离散噪声也产生相应的波动，此与仿真结果近似)。7叶片第1阶脉动频率(280 Hz)对应的噪声峰值(最小)为54.5 dB(A)，10叶片第1阶脉动频率(400 Hz)对应的噪声峰值(最大)为64.1 dB(A)，两者相差9.6 dB(A)。同时还可以看出7叶片、9叶片第1阶脉动噪声峰值的实验值比仿真值分别大3 dB(A)、2.6 dB(A)。可见，选择合适的叶片数量对离散噪声的影响很大。

图10 9叶片噪声频谱Fig.10 9 blade noise spectrum

图11 第1阶脉动噪声随叶片数变化情况Fig.11 Fluctuation noises of the first order vary with different number of blades

从4叶片至11叶片，总声压级的变化规律与离散噪声的结果一致，如图12所示。由图12可知，7叶片对应的噪声为71.8 dB(A)(最小)，10叶片对应的噪声为74.9 dB(A)(最大)，两者相差3.1 dB(A)，7叶片、9叶片实验值比仿真值分别大1.5 dB(A)、1 dB(A)。可见，离散噪声降低使得总声压级也相应降低。

图12 总声压级随叶片数变化情况Fig.12 Totalsound pressure levels vary with different number of blades

不同数量叶片对应的流量随全压的变化如图13所示。由图13可知，随着全压的增加，不同数量叶片对应的流量均减小，其中，4叶片至6叶片的风机流量明显不足，7叶片至11叶片的风机流量减小的幅度变缓，在高压下保持高流量的能力较强。在相同全压条件下，最大流量与最小流量的差别较大，以100 Pa为例，其差值达到2 558 m3/h。7叶片、9叶片对应流量的仿真值与实验值最大相差均不超过159 m3/h。

图13 不同数量叶片对应的流量随全压变化曲线Fig.13 Fluxes vary with total pressure corresponding to the different number of blades

将流量、转速等参数代入式(32)可得全压效率随流量的变化，如图14所示。由图14可知，效率均随着流量的增加先增大后减小。在风机的主要工作区域(683 m3/h≤qv≤3 930 m3/h)，7叶片至11叶片的效率均不低于35%，整体明显大于4叶片至6叶片的效率。综合来说，7叶片风机的效率最高(最高达到45%)，高效率的流量范围也较宽。7叶片、9叶片风机全压效率的仿真值与实验值最大相差均不超过2%。

图14 不同数量叶片对应的效率随流量变化曲线Fig.14 Efficiencies vary with flux corresponding to the different number of blades

3.3.2非等间距风机对噪声、流量及效率的影响

为了验证θB=2.406 rad为最优降噪的方案，选择9叶片风机进行仿真及实验分析(9叶片离散噪声较为明显，且为工程常用叶片)，在风机转速为2 400 r/min稳态条件下，仿真与实验结果在趋势上均是一致的，如图15～图18所示。

为了与理论相对应，对第1阶脉动噪声进行分析验证，其与最大调整角θB的关系如图15所示。由图15可知，第1阶脉动噪声值从大至小对应的最大调整角θB依次为0、0.9 rad、π rad、1.8 rad、2.7 rad、2.406 rad。最大调整角为2.406 rad相比0对应的第1阶脉动噪声降幅达到18.9 dB(A)。这两个调整角的实验值比仿真值分别大2.4 dB(A)、2.6 dB(A)。可见，最大调整角为2.406 rad方案对离散噪声的改善效果最明显，这与理论推导结果在趋势上是一致的。

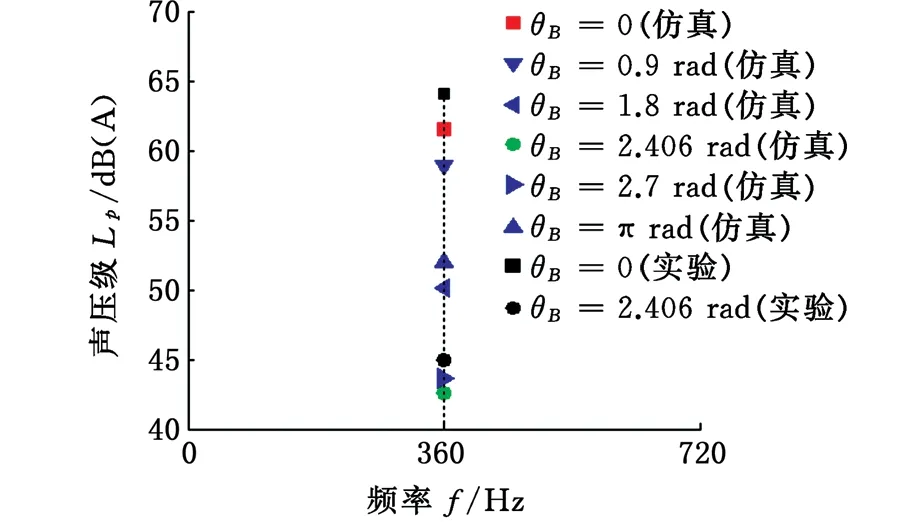
图15 第1阶脉动噪声随最大调整角θB变化情况Fig.15 Fluctuation noises of the first order vary with max adjustment angle θB

不同最大调整角θB对应总声压级的变化规律与离散噪声的仿真结果一致，如图16所示。由图16可知，最大调整角为2.406 rad相比0总声压级降幅2.2 dB(A)，以上两个仿真值与实验值分别相差1.2 dB(A)、0.5 dB(A)。

图16 总声压级随最大调整角θB变化情况Fig.16 Totalsound pressure levels vary with max adjustment angle θB

为了分析最大调整角θB为2.406 rad方案对流量的影响，进行了相应的流量随全压的变化分析，如图17所示。由图17可知，在相同全压条件下，最大调整角为2.406 rad与0对应流量的差别较小，以100 Pa为例，仅相差187 m3/h，此仿真值与实验值仅相差9 m3/h。

图17 θB=0与θB=2.406 rad时流量随全压变化的仿真值及实验值Fig.17 Simulation and experiment of θB=0 and θB=2.406 rad fluxes vary with total pressure

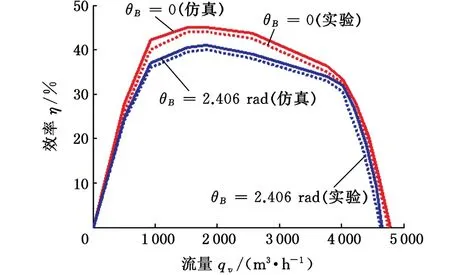
图18 θB=0与θB=2.406 rad时效率随流量变化的仿真值及实验值Fig.18 Simulation and experiment of θB=0 and θB=2.406 rad efficiencies vary with flux

为了分析最大调整角θB为2.406 rad方案对效率的影响，进行了相应的效率随流量的变化分析，如图18所示。由图18可知，在风机的主要工作区域(683 m3/h≤qv≤3 930 m3/h)，θB=2.406 rad与θB=0对应的效率均不低于35%，在相同流量下，最大差值为6.5%，此仿真值与实验值仅相差0.3%。

以上实验值与仿真模拟值的误差均在5%允许范围内，说明仿真模型是可靠的。误差主要是由于对风机模型进行了一定程度的简化、实验过程的测量误差以及仿真分析方法固有的误差等因素引起的。

4 结论

(1)针对等间距轴流风机，在2 400 r/min稳态条件下，随着全压的增大，各叶片的流量均减小；7叶片风机的效率最高(最大达到45%)，高效率的流量范围也较宽，而且在离散噪声和总声压级方面均最小，因此，从噪声、流量和效率综合来看，采用7叶片方案的风机效果最好，这在实验结果中也得到了验证，研究结果为风机叶片数量的选择提供了新的依据。

(2)通过理论分析提出了一种针对不同数量等间距叶片均采用最大调整角为2.406 rad即可达到最优降噪效果的方法，并且对流量及效率无明显影响,利用9叶片在2 400 r/min稳态条件下的仿真模拟与实验验证了这一结论。