埋地风管对空气冷却效果的影响因素
杨晓宇, 张 山, 刘斯佳, 张玲玲
(1.山东建筑大学 热能工程学院,山东济南250101;2.烟台大学,山东烟台264005)
1 概述
地道风系统(Earth to Air Heat Exchanger System,EAHES)是指利用储存在土壤中的地热能冷却或加热室外空气(或室内回风),并由机械送风或诱导式通风将处理后的空气直接送入室内或空气处理装置,以改善室内热环境[1-4]。本文仅供考虑地道风系统对空气冷却,采用横截面为正方形的混凝土埋地风管,对埋地风管出口空气温度、空气温降的影响因素进行计算分析。埋地风管出口空气温度指某个运行日换热结束时的埋地风管出口空气温度,空气温降指某个运行日换热结束时的埋地风管进出口空气温差。
2 地层原始温度
地道风系统降温工程中地层原始温度θ0的计算式为[5]40:
(1)
式中θ0——某一深度、某月地层原始温度,℃
θd——年平均地表面温度,℃
Δθd——地面温度波动振幅,℃
h——地层深度(认为与埋地风管的中心埋深相同),m
ω——温度波的角频率,rad/h
as——土壤的热扩散率,m2/h
tm——计算时间,h
T——温度波的波动周期,h,按全年365 d,每日24 h选取为8 760 h
式(1)中计算时间tm以7月31日24:00为计算起点,即7月的计算时间tm为0。计算8月某一深度的地层原始温度时,tm取7月的时间(即744 h)。计算9月某一深度的地层原始温度时,tm取7、8月的时间之和(即1 488 h)。
对于济南,年平均地表面温度θd取15.7 ℃,地面温度波动振幅Δθd取15.25 ℃,地层材料的热扩散率as取3.18×10-3m2/h[5]159。采用Fortran语言编程计算济南7~10月不同深度地层原始温度,见表1。通常认为地层深度3 m以下的土壤温度相对稳定[1],因此笔者选取地层深度4~10 m进行计算。对于济南地区,考虑供冷期采用地道风系统对空气进行冷却处理,供冷期集中在7~10月。即地道风系统运行时间为7~10月,鉴于土壤温度的恢复功能,认为次年7~10月不同深度的地层原始温度仍按表1选取。
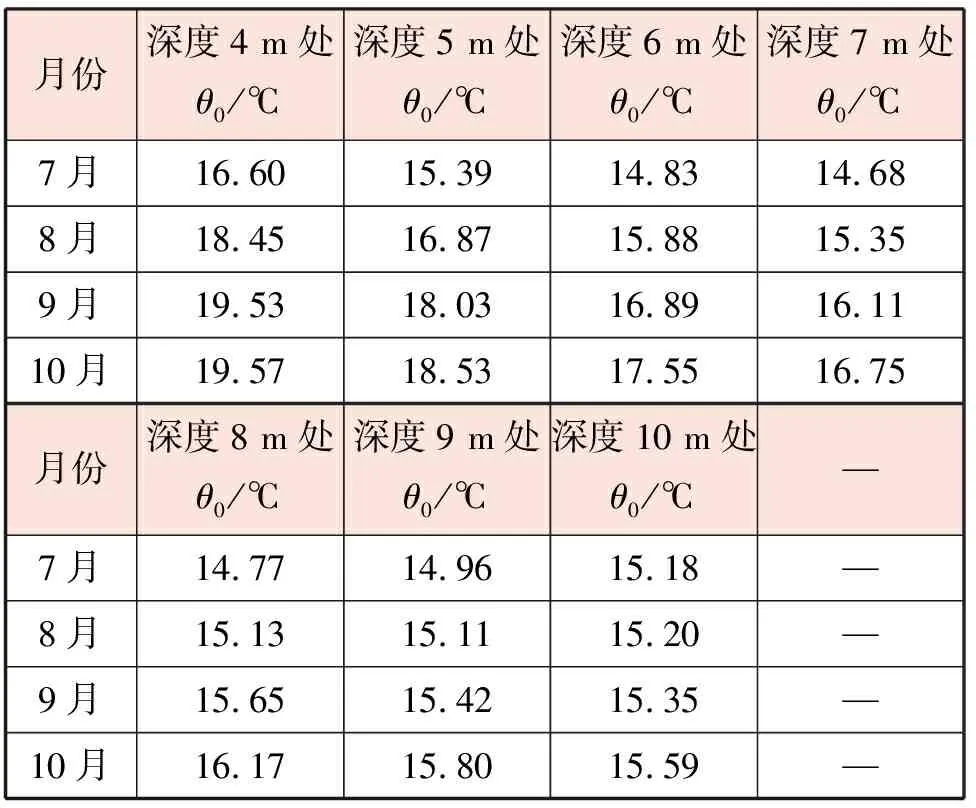
表1 济南7~10月不同深度的地层原始温度
3 模型建立
3.1 物理模型
埋地风管(横截面为正方形)物理模型见图1。由图1可知,埋地风管中心埋深为h,起始时刻的地层温度为θ0。埋地风管全长为L,质量流量为qm的空气均匀流过埋地风管,埋地风管进口空气温度为θin,与埋地风道壁面传热后,埋地风管出口空气温度为θout。
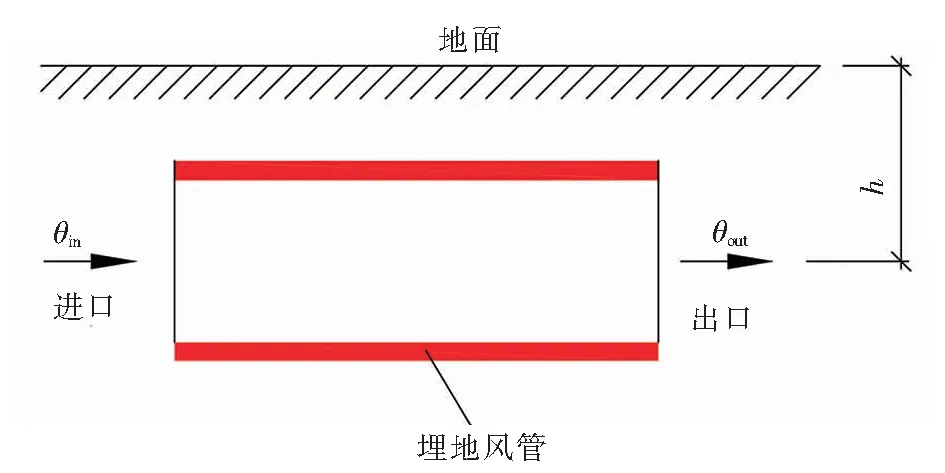
图1 埋地风管物理模型
3.2 数学模型
在物理模型中沿空气流动方向取微元,根据热平衡原理建立积分方程,并进行积分得到:
(2)
式中K——埋地风管壁面不稳定传热系数,W/(m2·K)
A——埋地风管壁面面积,m2
cp——空气的比定压热容,kJ/(kg·K),本文取1.005 kJ/(kg·K)
qm——空气质量流量,kg/s
θout——埋地风管出口空气温度,℃
θin——埋地风管进口空气温度,℃
① 日连续运行
日连续运行是指地道风系统运行日24 h连续运行。整理式(2)可得到日连续运行条件下,埋地风管出口空气温度θout,con的计算式为:
θout,con=θ0+(θin-θ0)·
(3)
式中θout,con——日连续运行条件下埋地风管出口空气温度,℃
埋地风管壁面不稳定传热系数K的计算式为[5]45:
(4)
(5)
式中aw——埋地风管壁面热扩散率,m2/s,本文取7.556×10-7m2/s
t——地道风系统运行时间,h
β——形状修正系数
λ——埋地风管壁面热导率,W/(m·K),本文取1.74 W/(m·K)
α——埋地风管内壁表面传热系数,W/(m2·K)
s——埋地风管横截面周长,m
λa——空气热导率,W/(m·K),本文取0.026 7 W/(m·K)
de——埋地风管当量直径,m
Re——空气的雷诺数
u——空气流速,m/s,本文取2 m/s
υ——空气的运动黏度,m2/s,取15.961×10-6m2/s
As——埋地风管内壁面横截面面积,m2
对于年间歇运行方式,在计算第m日结束时埋地风管出口空气温度时,式(4)、(5)中的运行时间t应取24 h的m倍。
② 日间歇运行
日间歇运行是指地道风系统运行日工作时间少于24 h的情况。日间歇运行条件下,埋地风管出口空气温度θout,d的计算式为[5]46:
θout,d=θ0+(θin-θ0)·
(6)
式中θout,d——日间歇运行条件下埋地风管出口空气温度,℃
n——换热周期数,取2的整数倍
Ki——对应每一换热周期相应计算时间的不稳定传热系数,W/(m2·K)
式(6)中的n取2时,对应第2个运行日换热结束时的时间,即24 h+t0,t0为每日的运行时间,单位为h。当n取4时,对应第3个运行日换热结束的时间,即48 h+t0,以此类推。当计算第1个运行日换热结束时的埋地风管出口空气温度时,将t0代入式(3)~(5)进行计算。
对于式(6)中的Ki,是将式(4)、(5)中的t替换成ti进行计算的。
当i为0或偶数时,有:
ti=t0+12i
式中ti——第i个计算时间,h
t0——第一日运行时间,h
当i为奇数时,有:
ti=12(i+1)
3.3 数学模拟求解
笔者采用Fortran语言编程,求解数学模型。
4 模拟结果及影响因素分析
埋地风管横截面为正方形,内壁面横截面尺寸为1 m×1 m。运行地点为济南,运行起始时间为7月1日0:00,地层原始温度按埋地风管中心埋深选取。埋地风管进口空气温度取济南7月平均室外温度27.5 ℃,空气流速为2 m/s。
① 中心埋深
埋地风管长度为100 m,仅运行1次,运行时间为8 h。中心埋深变化范围为4~10 m,变化步长为1 m。空气温降随中心埋深的变化见图2。由图2可知,随着埋地风管中心埋深的增大,空气温降先增大后减小。当埋地风管的中心埋深为7 m时,空气温降最大。当埋地风管中心埋深为6 m时,空气温降与埋地风管中心埋深为7 m时非常接近。考虑工程经济性,埋地风管的中心埋深宜选取6 m。
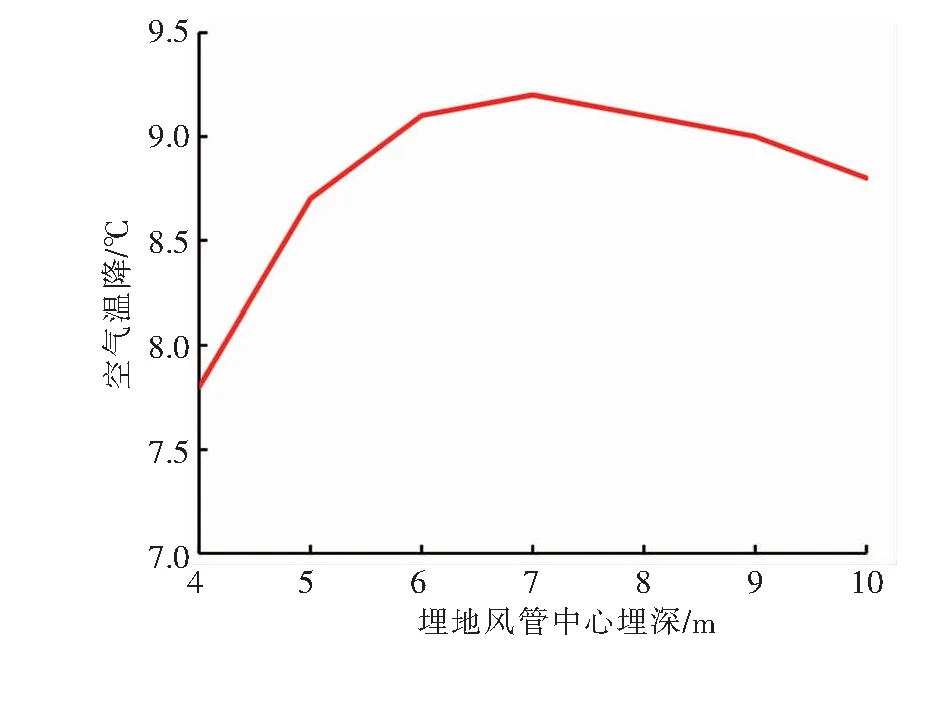
图2 空气温降随中心埋深的变化
② 运行方式
埋地风管长度为100 m,中心埋深为6 m。运行方式分别选取日连续运行方式、日间歇运行方式1、日间歇运行方式2,3种运行方式的运行日均为30 d。日连续运行方式全天24 h运行,日间歇运行方式1每日运行8 h,日间歇运行方式2每日运行16 h。3种运行方式埋地风管出口空气温度、空气温降随运行日的变化分别见图3、4。
由图3可知,3种运行方式的埋地风管出口温度均随着运行时间的延长而上升。在3种运行方式中,日间歇运行方式1的埋地风管出口温度最低,日间歇运行方式2居中,日连续运行方式最高。由图4可知,3种运行方式的空气温降均随着运行时间的延长而下降。在3种运行方式中,日间歇运行方式1的空气温降最大,其次是日间歇运行方式2,日连续运行方式最小。这说明,与日连续运行方式相比,日间歇运行有利于土壤温度的恢复。对于日间歇运行方式,短时间运行更有利于土壤温度的恢复。

图3 3种运行方式埋地风管出口空气温度随运行日的变化

图4 3种运行方式空气温降随运行日的变化
③ 埋管风管长度
仅运行1次,运行时间为8 h,埋地风管中心埋深为6 m。埋地风管的长度变化范围为50~400 m,变化步长为50 m。空气温降随埋地风管长度的变化见图5。由图5可知,空气温降随埋地风管的长度增大而增大,当埋地风管的长度达到250 m后空气温降的增幅不再明显。这说明,埋地风管存在合理长度,不同工程应进行区别计算。
5 结论
① 随着埋地风管中心埋深的增大,空气温降先增大后减小,存在最佳中心埋深。
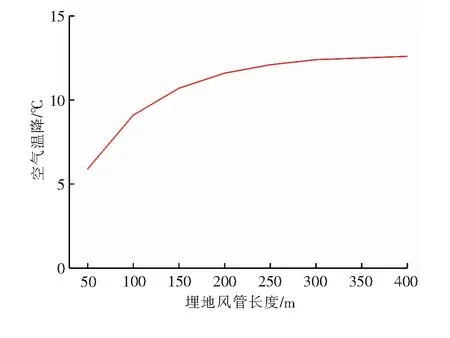
图5 空气温降随埋地风管长度的变化
② 运行方式选取日连续运行方式(全天24 h运行)、日间歇运行方式1(每日运行8 h)、日间歇运行方式2(每日运行16 h),3种运行方式的运行日均为30 d。3种运行方式的埋地风管出口空气温度均随着运行时间的延长而上升。日间歇运行方式1的埋地风管出口温度最低,日间歇运行方式2居中,日连续运行方式最高。与日连续运行方式相比,日间歇运行有利于土壤温度的恢复。对于日间歇运行方式,短时间运行更有利于土壤温度的恢复。
③ 空气温降随埋地风管的长度增大而增大,当埋地风管达到一定长度后空气温降的增幅不再明显,埋地风管存在合理长度。

