物像空间位姿表征模型及标定技术研究

冯志伟， 陈 欣， 李重阳， 王英伟*

(1. 北京理工大学 深圳研究院， 广东 深圳 518057； 2. 北京空间机电研究所， 北京 100083)

1 引言

图像测量以及机器视觉应用在研究物体几何尺寸及其在空间的位姿等方向上具有很强的需求背景，是该领域较为活跃的研究热点之一，具有非接触、高精度的优点。常见的视觉测量方法主要有单目视觉测量、双目视觉测量、结构光视觉测量等[1-4]。

单目视觉测量仅需一个视觉传感器，因此该方法结构简单、摄像机标定简单，同时也避免了立体视觉中的立体匹配难的不足，近几年这方面的研究比较活跃。王鹏等[5]运用单目视觉定位图像中特征点及求解空间位姿，通过在距离因子的基础上建立非线性的位姿测量模型，利用代数变换将位姿模型线性化处理，最终利用线性方程求解，不仅有效抑制了图像噪声的干扰，同时提高了位姿测量的精度。尹英杰等[6]利用单目视觉测量模型对平面靶标上特征点进行标定，根据图像坐标计算出被测平面坐标位置，实现目标的定位及长度测量。双目视觉测量虽可以达到较高的精度，但相较单目视觉测量具有结构复杂、测量时间长等缺点[7]。结构光视觉测量主要采用结构光形成的特征，根据三角测量原理求取特征点的三维坐标信息，抗干扰能力强、实时性好，但系统标定比较困难。孙军华等[8]提出一种不需要计算光平面标定点的线结构视觉传感器标定方法，通过求解平面靶标上光条空间直线的Plǜcker矩阵得到光平面在摄像机坐标系的平面方程，最后通过非线性优化方法得到在最大似然准则下的最优解，实验证明此方法比现有方法标定精度提高30%左右。

本文基于单目视觉三维空间测量原理，通过平面镜反射及摄像机的标定，实现系统的三维空间定位，在较高的精度基础上提高了空间测量范围。通过验证摄像机标定精度，完成对条纹反射系统的空间测量，对于图像测量及计算机视觉中的系统标定问题具有指导性意义。

2 系统空间位姿

在三维形貌测量系统整体标定中，三维空间点与二维图像点是利用摄像机模型联系起来的。摄像机模型是光学成像模型的简化，分为线性模型和非线性模型两类。实际中的成像系统属于非线性模型，由于与物空间坐标和图像空间坐标近似线性关系，对摄像机内参数的计算可归结为求解线性方程组，计算简单，因此摄像机标定多以线性模型为基础。

2.1 摄像机标定原理

小孔模型是各种摄像机模型中最简单的一种，在不考虑成像畸变下近似一个线性模型，主要描述空间景物点和成像点之间的位置关系。如图1[9]所示，以空间一点Ow为坐标原点建立物空间坐标系OwXwYwZw，点P在物空间坐标系下的坐标为(xw,yw,zw)。以摄像机的光轴与图像平面的交点Oi为坐标原点建立摄像机图像坐标系OiXY，其中X轴平行于像素横向阵列，Y轴垂直于X轴。以摄像机的光学中心o为坐标原点，光轴方向为z轴建立摄像机坐标系oxyz，其中x轴和y轴方向分别平行于图像坐标系的X轴和Y轴方向。有效焦距f是图像平面与光心的距离，(Xu,Yu)是理想小孔成像模型下P点的图像坐标，(Xd,Yd)是考虑镜头畸变得到的实际图像坐标。

图1 小孔成像原理Small hole imaging principle

点P在物空间坐标系下与摄像机坐标系下的转换关系可表示为：

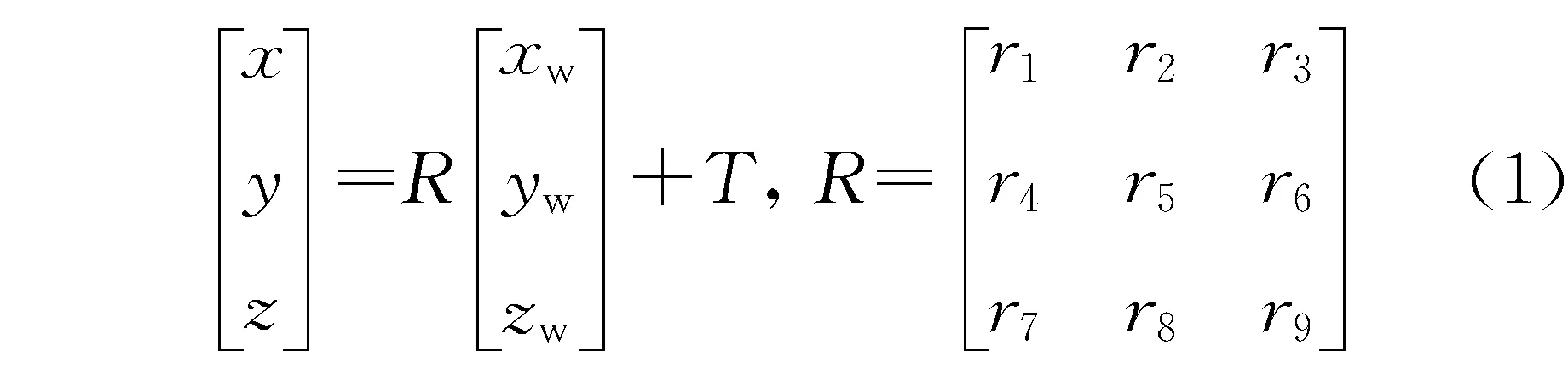
式中，R为3×3的旋转矩阵，T为3×1的平移矢量。

将点P由摄像机坐标系下转换到图像坐标系下，理想的投影变换为：

(2)

得到P点在图像坐标系下的坐标(Xu,Yu)，若标定出成像畸变参数，则可进一步得出实际图像坐标(Xd,Yd)。

2.2 LED屏幕空间位置测量原理

根据上面的摄像机标定，通过在参考平面放置棋盘格，可以很精确地获得参考平面的空间位置。LED显示屏显示棋盘格图像，摄像机获取由参考平面镜反射的镜像棋盘格图像。根据截断相位提取局部两点作为特征点，由此计算摄像机图像平面和该镜像平面的映射关系，得到镜像平面的旋转矩阵和平移矩阵。

LED显示屏镜像的空间位置的原理如图2[10]

图2 LED显示屏空间位置原理图Schematic diagram of LED display location

所示，首先在LED镜像平面上取一点C″(x3,y3,z3)，该点与摄像机光心O的连线OC″通过参考平面且交于C(x1,y1,z1)点，LED显示屏上点C′(x2,y2,z2)对应镜像平面中点C″。镜像变换也就是对称反射变化，显示屏镜像相对于参考平面作对称变化，用矩阵表示为：

(3)

式中，TC为摄像机坐标原点到C点的平移矩阵，Rp为摄像机坐标系到世界坐标系下参考平面的旋转矩阵，R0为对参考平面的对称反射变换，且：

由此可计算出点C′在摄像机坐标系下的坐标：

[x2,y2,z2,1]=[x3,y3,z3,1]×Rab

(5)

在镜像平面上取多个特征点，计算出LED显示屏上对应的坐标，从而求出LED显示屏平面相对于摄像机坐标系的旋转矩阵Rs和平移矩阵Ts，最终确定LED显示屏平面的空间位置。

3 标定实验

采用MATLAB自带棋盘格标定程序进行标定，首先验证标定的准确度，得到相对误差值。在准确度满足实验要求的前提下，标定出待测平面镜和LED显示屏的三维空间位置。

3.1 标定误差实验

实验以水平放置于试验台上的标定板为参考平面，在待测的标定板下放入一个楔形，楔角为20.1314°，沿图3中所示方向随意摆放4个位置，对比4个位置处待测板与参考平面的夹角与实际楔角的角度，计算标定的相对误差。

图3 摄像机标定实验示意图Schematic diagram of calibration experiment

待测板的切斜角度，可用矩阵表示为：

(6)

式中，R21表示待测平面相对参考平面的旋转矩阵，R2为待测平面坐标系与摄像机坐标系的旋转矩阵，R1为参考平面坐标系与摄像机坐标系的旋转矩阵的逆矩阵。

旋转矩阵的角度转换公式见式(7)。

实验结果如表1所示。通过实验验证的结果可以看出，测量值与实际值之间的相对误差很小，标定的平均相对误差在可接受范围内。

式中，α、β、γ分别为相对摄像机坐标系x轴、y轴、z轴的偏转角。

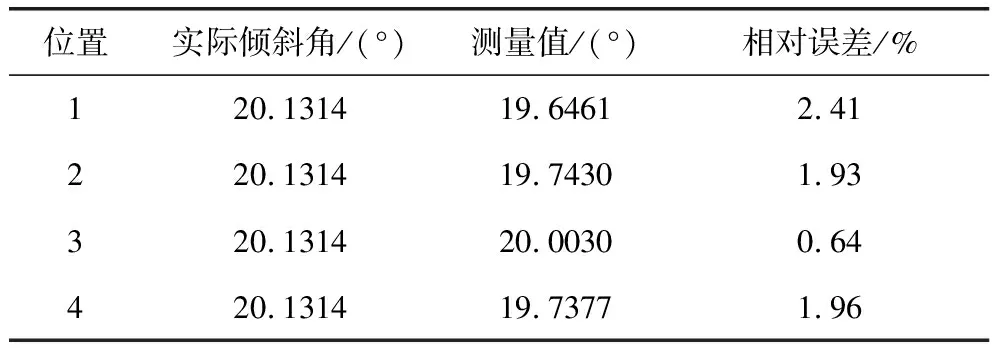
表1 标定实验实际值与测量误差

3.2 待测镜、LED屏幕三维空间位置的标定

使用高精度的标准平面反射镜辅助单目视觉对条纹反射检测系统的实物图和实验结果如图4和图5所示，图5中红色平面是LED显示屏在摄像机坐标系下的平面位置，蓝色平面是CCD采集到的虚拟显示屏面，绿色平面是标准平面镜所在平面。

图4 条纹反射检测系统实物图Fringe reflect testing instrument

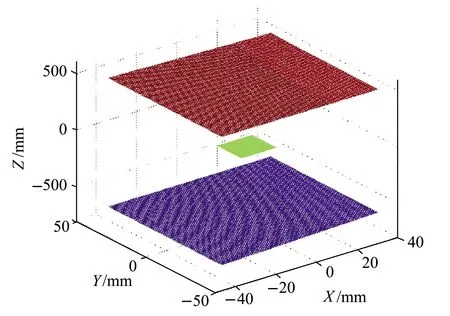
图5 LED显示屏空间位置坐标Coordinate location of LED display

4 总结

本文基于单目视觉测量的基本原理，利用标准平面镜辅助三维空间测量，系统标定由LED显示棋盘格提供输入数据，无需精密立体标定块和精确移动装置，操作简单，在保证较高精度的情况下扩大了空间测量范围。同时，实验验证了摄像机标定的误差在可接受范围内，保证了单目视觉系统在空间测量上的准确度，适用于图像测量及计算机视觉中的应用。