均质地基中纵截面异形桩受扭弹塑性分析

张海峰 孔纲强 邹新军 车平

摘   要：为了探讨纵截面异形桩的受扭性状，考虑桩身纵向变截面特性，将桩-土体系沿深度方向划分为有限个微元段，建立均质地基中纵截面异形桩受扭弹塑性分析理论模型;基于传统圆形桩桩顶T-φ曲线与桩身扭矩、转角关系曲线，推导获得纵截面异形桩的桩身扭矩和扭转角近似解答，并基于MATLAB编制了相应的计算程序.继而，初步探讨了纵截面异形桩与等截面圆形桩受扭性能的异同点，并开展楔形桩受扭性能影响因素分析.研究结果表明：上端桩身直径对抗扭承载性能影响显著;等体积混凝土用量下，纵截面异形桩的抗扭性能相对优于等截面圆形桩，且楔形桩抗扭性能最优;相同桩顶扭矩荷载下，楔形桩抗扭承载力随桩身剪切模量、桩径、楔角的增加而增大，桩径提高1倍，桩顶抗扭承载力提高3～5倍.

关键词：桩基;纵截面异形桩;扭矩荷载;弹塑性分析

中图分类号：TU473.1                             文献标志码：A

Abstract：In order to study the torsional behavior of longitudinal special-shaped piles， a longitudinal cross-section pile torsion elasto-plastic analysis model was built in homogeneous soil ground. The model considers variable cross-section of the special-shaped pile， and the pile-soil system along the depth direction is divided into finite segments. Based on the T-φ curve at traditional circular pile top and the torque-angle distribution curves along the pile shaft， the corresponding formula was obtained. The calculation program was run through MATLAB software. The torsional behaviors of longitudinal special-shaped piles and uniform circular piles were comparatively analyzed. The optimum design parameters for tapered pile were analyzed. The results show that the torsional performance is influenced by the top pile diameter obviously. The torsional performances of longitudinal cross-section special-shaped pile are relatively better than those of uniform circular pile with the same concrete usage. The torsional bearing capacity of tapered pile increases with the increase of the shear modulus， diameter， and taper angle， and the torsional bearing capacity is improved to 3～5 times under two times diameter.

Key words：pile foundation;longitudinal special-shaped pile;torque load;elastoplastic analysis

海上結构桩基础通常受到风力、水流等水平偏心荷载的作用，导致其桩基承受相对较大的扭矩.若忽略这类扭矩荷载的作用，工程将会偏向不安全，甚至发生破坏[1].因此，研究桩基受扭问题，尤其是扭矩荷载与其它水平、竖向等荷载耦合作用下的桩基性状具有重要意义[2].关于单桩受扭特性的研究，主要可分为两大类：

1）单桩扭转与轴向受荷相关性研究.Stoll[3]开展了两根管桩的现场受扭试验，通过桩抵抗扭矩所需的贯入深度确定桩承受轴向荷载所需的贯入深度，扭转受荷与轴向受荷相应有着类似的性质.Poulos[4]在高岭土中进行了轴向受荷和扭转受荷小比尺模型试验，利用轴向受荷试验得到的土体参数，通过模拟计算得到单桩受扭下的扭矩-转角曲线，证明了桩扭转与轴向受荷响应之间的相关性.Georgiadis[5]认为桩对扭矩和轴向荷载的承载都是通过桩侧摩阻力实现的，且桩侧总侧摩阻力为两者的矢量和;假定轴向与扭矩荷载共同作用时的总侧摩阻力为定值，由此提出了单桩扭转与轴向受荷共同作用时的分析模型.Georgiadis和Saflekou[6]通过小比尺模型试验得到扭转与轴向荷载之间相互削弱的结论，验证了桩扭转承载力的本质是桩侧摩阻力的发挥.邹新军等[7]基于水平力与扭矩组合加载装置开展了单桩模型试验，发现桩顶在扭矩与水平力组合作用下，极限承载力较单一受水平力或扭矩均有所减小.

2）扭转荷载下单桩抗扭转承载能力问题研究.

Poulos[4]利用弹性理论建立了圆形桩单桩桩顶受扭矩荷载的扭转计算方法，并列出了桩头的扭矩-转角的参数解;Randolph[8]假设土体为理想弹塑性模型，得到了单桩桩头扭转响应的闭合解;但是，这两种解法均不能得到桩身的应力和转角分布，不利于对整个桩身内力进行系统分析.Dutt等[9]分别在松散干砂与密实干砂中采用圆桩与方桩进行了试验，发现土体密实度与桩型均能影响桩身的受扭形状.Chow[10]提出了单桩计算的离散单元法，由于该方法对桩身划分了单元，因此可以考虑土体分层等情况，且能得到桩身各单元的应力与转角，但其解答仅适用于桩侧土体的弹性阶段.Zhang和Kong[11]利用离心机在砂土中开展了单桩扭转试验，得到了典型的单桩扭转曲线.邹新军等[12]假定成层土中各土层单元均质，基于平衡原理获得桩身微段扭矩递推计算式，进而获得桩头及桩身的扭矩-扭转角分布曲线，桩顶扭矩沿桩身的传递主要发生在浅部土层中.吴文兵等[13]建立了动态扭转荷载下，楔形桩与桩侧土耦合扭转振动的定解问题，讨论了桩身参数对楔形桩扭转振动特性的影响规律.

近年来，为了优化桩基承载性能、提高单位混凝土材料利用率，国内外相关学者提出了横截面异形桩和纵截面异形桩等新型桩基形式;这些桩型具有承载力大、单位混凝土用量低、用途广等技术优点.所谓横截面异形桩是通过改变桩横向截面几何形状得到的异形桩，如Y形桩、X形桩等[14-15];纵截面异形桩即通过改变桩身纵向截面形状得到的变截面异形桩，目前常用的纵截面异形桩有楔形桩、扩底楔形桩、竹节桩等[16-19].然而，针对扭剪荷载下异形桩桩基承载性能的研究仍相对较少.因此，本文考虑纵截面异形效应，将其桩身沿竖向划分为多个微元段，基于已有桩身微元段递推计算式[12]，推导获得纵截面异形桩的桩顶与桩身扭矩转角关系式;针对楔形桩、扩底楔形桩和竹节桩等3种纵截面异形桩，开展其受扭承载特性对比研究，并针对楔形桩开展系统的影响因素分析，以期为纵截面异形桩的扭转特性计算与设计提供技术支撑.

1   理论模型的建立与验证

1.1   基本假定

楔形桩、扩底楔形桩和竹节桩等3种纵截面异形桩的桩-土系统相互作用的模型如图1所示.将桩-土系统沿竖直方向划分为n个微元段，各微元段分别标识为1，2，3，…，j，…，m，…，n;其中，扩底楔形桩桩身扩大头的楔形段均匀分为m段，擴大头的圆形段无需分段，非扩底段均匀分为n-m段，则扩底楔型桩第j微元段桩径dj计算式为：

同理，可得楔形桩在竖向均匀划分为n段时，第j微元段桩径计算式为：

式中d1、d2和D为分段桩径.

为了简化分析，理论模型基本假定如下：

1）楔形桩与扩底楔形桩为各向同性、竖直、圆形变截面锥体，分段后桩的每一微元段为圆柱体，土层物理性质不变，即为均质地基;

2）桩侧土处于弹性阶段时，桩-土扭转位移协调;

3）随着桩顶扭矩的增加，桩侧土塑性区由上至下逐渐开展，桩-土系统的破坏以桩侧土塑性区开展至桩底处为准.

1.2   纵截面异形桩-土体系受扭响应方程及其求解

1.2.1   弹性阶段

采用荷载传递法中双折线和指数非线性两种模型分析竖向受荷桩.对于均质各向同性弹性介质中的桩给出了土体初始抗扭刚度k的计算式：

邹新军等[12]采用桩身荷载传递双折线模型，由平衡条件提出了圆形桩桩侧土处于弹性阶段下，桩身扭转控制方程及边界条件：

式中：TB 和φB分别为桩端处的扭矩与扭转角;Gp和Jp分别为桩身的剪切模量与极惯性矩.

式中：KB为系数，KB = 16GSB r03/3，GSB为桩端处桩侧土的剪切模量.

由式（4）（5）即可推得桩顶扭矩与转角为：

桩顶处桩身扭矩与扭转角之比为：

当桩身按图1所示分段且桩侧土处于弹性阶段时，可得到第i个桩土微元段的桩身扭转控制方程及边界条件为：

式中：zi为第i段底部深度（m）;Ti+1和φi+1分别为第i桩段底部的扭矩及扭转角;ki为第i桩段桩侧土的抗扭刚度;同理令bi = [ki/（GpJp）]0.5，可以解得第i桩段顶部的扭矩Ti和扭转角φi分别为：

在某一桩顶扭矩下，由式（9）可逆向导得弹性阶段第i桩段底截面的扭矩和扭转角递推公式为：

1.2.2   塑性阶段

当桩顶扭转角大于φu时，随着桩顶扭矩的增加，桩侧土由上至下逐渐进入塑性阶段，假定塑性区开展深度为ld，则ld以上为塑性区，桩土位移不再协调，ld以下为弹性区，对于塑性阶段有桩身受扭控制方程及边界条件：

式中Td和 φd分别表示ld深度处桩身的扭矩和扭转角.

同理可得，异形桩桩侧土处于弹塑性阶段时，设塑性开展深度ld = zi时可得第 个桩土微元段的桩身扭转控制方程及边界条件为：

式中Td和φd可由式（9）通过边界条件Tn+1与 φn+1迭代计算得到.

由（13）可解得第i桩段桩顶的扭矩与转角为：

对于桩侧土处于塑性状态的桩段，顶端截面的扭矩与转角递推计算公式为：

在某一桩顶扭矩下，由式（15）可反推得塑性段第i桩段底截面的扭矩和扭转角递推公式为：

1.2.3   竹节桩变截面处与土体接触面相互作用分析

对竹节桩而言，在变截面处，控制方程只考虑桩侧土体的作用（即图2中AB、HG、FE、CD处土体接触的作用），不考虑桩身变截面处与土体接触的作用（即图2中BC、FG处土体接触的作用）.竹节桩扭转过程中，其桩身变截面处与土体接触引起的滑动摩擦力能提供部分扭矩，故本节将该部分扭矩定量计算后与根据桩侧土体接触计算得到的桩体抗扭承载力进行对比，进行定性分析.

取桩身剪切模量为25 GPa，其余参数如上，可得竹节桩其桩身变截面处与土体接触引起的滑动摩擦力能提供最大扭矩值为0.027 6 MN·m;而由桩侧截面与土体接触的扭矩承载力为3.794 5 MN·m.计算可得桩身变截面处扭矩承载能力为总抗扭承载力的0.7%，故可不考虑该部分的影响.

1.2.4   计算步骤

主要计算步骤如下：

1）将异形桩划分为n个单元，确定单元桩-土体系微元段的几何与力学参数（li，GP，Jpi）及土层力学参数（ki，φu，Gs）.

2）当桩-土体系处于弹性阶段时，由式（10）递推计算得到桩顶扭矩与转角的比值K1，按T1 = K1φ计算桩顶扭矩转角曲线，并按照式（11）迭代计算此时桩身扭矩转角的分布.

3）当桩侧土由上至下开始进入塑性阶段时，以塑性区开展深度ld为变量，计算桩顶的T-φ曲线和桩身的扭矩转角分布曲线.ld=0时，取桩顶扭转角为土体抗扭极限扭转角φu，按式（11）递推计算弹塑性极限扭矩值.ld>0时，当ld所对应的点位于某个桩段时，则以该点为界将桩段再细分为两个桩段，其余桩段划分不变.

4）分别按式（11）与式（16）递推计算弹性区和塑性区的桩身扭矩转角曲线.不断增加ld进行循环计算，直至ld=L时即可获得桩顶的T-φ曲线.

1.3   微元段分段精度分析

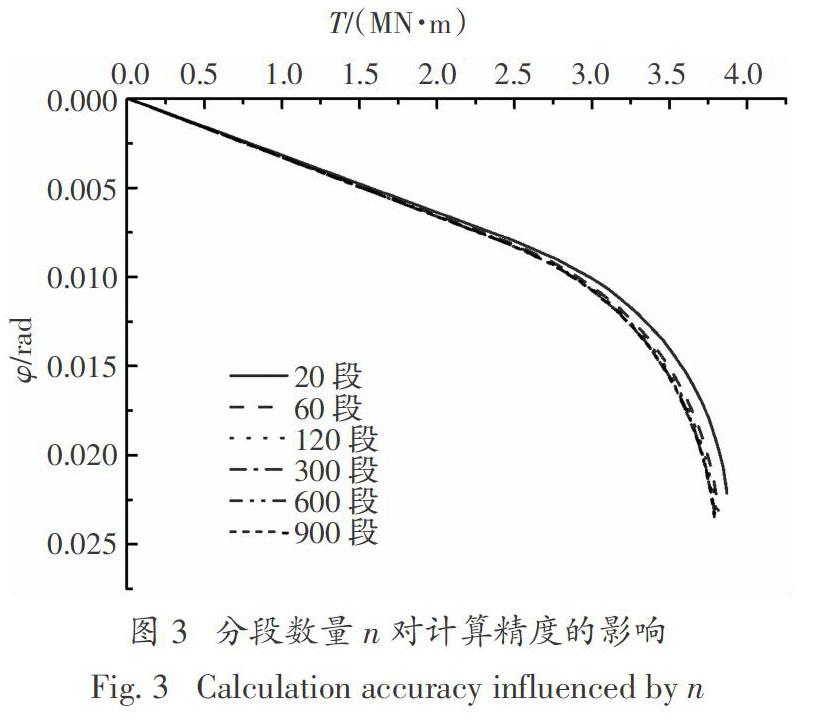
选取扩底楔形桩作为研究对象，分析微元段划分数量对解法的可靠性和精度的影响.几何参数选取为分段桩长h1=28.5 m，h2=1.5 m;分段桩径d1=1.338 m，d2=0.675 m，D=1 m;取桩周土参数为：剪切模量Gs=5 MPa，φu=0.008 rad.微元段划分数量n对计算精度的影响如图3所示.由图3可见，微元段划分数量过少时，桩顶扭矩计算偏大，扭转角计算偏小，当微元段数逐渐增加，计算得到的桩身扭矩转角曲线趋于一致：当n>300时，计算得到的曲线基本不再改变，计算结果能够满足精度要求;因此，后续计算中扩底楔形桩与楔形桩统一沿竖向等长度划分为300个微元段.

1.4   理论模型验证与分析

将文中解答退化为等截面圆形桩后与文献[10]基于离散元的方法一同利用文献[3]的pile-3桩试验参数进行计算并与其扭桩试验结果进行对比验证.Pile-3桩为桩长17.4 m、外径0.273 m、壁厚6.3 mm 的钢管桩;桩内浇注混凝土，桩身扭转刚度为（GJ）P=12.8 MN·m2;桩周土的土体剪切模量为4.59 MPa;弹性极限扭转角φu为0.001 5 rad.

基于本文解答以及文献[10]离散元法获得的桩顶扭矩-转角曲线与实测曲线的对比分别如图4所示.由图4可知，本文解答在弹性及塑性区开展初期阶段与实测结果吻合相对较好，而文献[10]解答高估了弹性阶段桩头的转角，在较大桩顶扭矩尤其是0.02 MN·m之后本文方法和文献[10]都与实测值出现了相对较大偏差;可能原因在于随着桩顶扭矩的增大，桩身承担的扭矩和转角逐渐增大导致了桩内回填混凝土的渐进开裂、钢管与回填混凝土的相对滑移，本文理论模型中未能考虑这些因素的影响.而本文方法与文献[10]对抗扭极限承载力的预测相近，都很靠近实测值，故本文理论解答可以一定程度上预测桩顶扭矩-转角曲线，尤其在允许工作荷载作用情况下，因此，可用于预测极限抗扭剪承载力.

2   受扭承载性能对比分析

桩身材料用量与桩周土力学参数相同情况下，将楔形桩、扩底楔形桩和竹节桩等3种纵截面异形桩与等截面圆形桩的抗扭承载性能进行对比.各类型桩尺寸分别为：1）等截面圆形桩尺寸为r0=0.5 m，L=30 m;2）扩底楔形桩桩分段桩长h1=28.5 m，h2=1.5 m;分段桩径d1=1.338 m，d2=0.675 m，D=1.0 m;3）楔形桩桩长h=30 m，顶端桩径d1=1.352 m，底端桩径d2=0.6 m;4）竹节桩由上至下分节桩径分别为：d1=1.058 8 m，d2=0.998 8 m，d3=0.938 6 m.桩周土参数为：剪切模量Gs=5 MPa，极限扭转角φu=0.008 rad，土体重度γ=20 MPa.桩身剪切模量GP选取2 GPa与25 GPa 2种情况.

2.1   桩身扭矩、转角分布对比分析

由图5可知，桩身剪切模量取25 GPa，在相同的桩顶扭矩1.5 MN·m下，3类纵截面异形桩的桩身扭矩沿深度方向上的减小速度较为接近，但都明显快于等体积的等截面圆形桩;楔形桩减小速度最快，竹节桩与扩底楔形桩次之;由于桩頂扭矩由桩侧土承担，任意深度处桩身扭矩之于桩顶扭矩的减小值即为桩顶至该深度处桩侧土承担扭矩大小的总和.

由此可得：相同条件下，纵截面异形桩桩侧土对桩顶扭矩荷载的承载在上部土层完成更多;桩顶扭矩沿桩身的传递都主要发生在上部土层中，与纵截面形式无关.另外，在桩身上部，3类异形桩中扩底楔形桩与楔形桩的桩身扭转角分布较为接近，都要小于等体积的竹节桩，而圆形桩分布转角较大.

2.2   桩顶T-φ曲线对比分析

由图6可知，在相同的桩顶扭矩荷载作用下，3种纵截面异形桩桩顶产生的扭转角度相近，都明显小于等体积的等截面圆形桩，且其中楔形桩扭转角度最小，竹节桩与扩底楔形桩次之;在相同的桩顶扭转角下，3种纵截面异形桩桩顶承受的扭矩相近，均高于等体积的等截面圆形桩，且其中楔形桩桩顶承受扭矩最高，竹节桩与扩底楔形桩次之.由此可得，等体积的纵截面异形桩抗扭承载性能要好于等截面圆形桩，且楔形桩抗扭性能最佳，由微元段土体抗扭刚度的计算公式ki = 4πri2Gs易知，当微元段桩径越大时，土体初始抗扭刚度也就越大.桩侧土对桩顶扭矩的承载主要发生在上部土层，因此上部体积较大的异性桩有着更好的抗扭承载性能.

3   影响因素分析

由第2节可知，楔形桩有着相对最优的抗扭承载性能;因此，针对楔形桩进行系统参数分析;考虑桩身剪切模量GP、桩径d1、d2以及楔角 等因素影响.

3.1   桩身模量对抗扭承载性能的影响

分别取桩身材料剪切模量GP为2 GPa、16 GPa、25 GPa和65 GPa进行对比分析.桩身尺寸与桩周土的力学参数与上节中选取相同.由图7可见，桩顶扭矩保持不变时，楔形桩桩顶扭转角随GP的增加而减小;对于某一桩顶扭转位移控制值，桩顶所能承受的扭矩随GP的增大而显著增加，即桩身抗扭能力随着GP的增加而不断提高.

3.2   楔形角对抗扭承载性能的影响

为了探讨楔角的影响，控制体积相等取楔角分别在0.5°，0.716 2°，1°和0°（圆形桩）进行对比分析，其余参数同上.由图8可知，等体积的楔形桩随着桩型越“尖”，即楔角越大，桩-土系统抵抗桩顶扭矩荷载的性能越好，该参数分析结论与吴文兵等在扭转振动荷载下得到的结论一致.而随着楔形角的增大，承载性能的增加幅度会越来越小;因此，在进行受扭性能设计时，适当考虑增加楔角来达到提高受扭承载性能的目的，可见楔形桩在静动荷载下增大楔角都对抗扭承载力有着增强作用.