不同初始分布向列相液晶电容特性的相场法研究
王舒凯,周志东
(厦门大学 材料学院,福建省特种先进材料重点实验室,福建 厦门361000)
1 引 言
20世纪50年代末,发现了液晶材料在热图像方面的应用价值,激发了人们对液晶的研究热潮[1]。液晶盒又称液晶显示板,是将薄层液晶注入到两块玻璃基板之间,加以密封。当施加外电场时,液晶分子的排列状态和指向矢发生改变,从而改变液晶盒宏观的电学和光学特性。液晶盒也可以当作一个电容器[2],液晶层的有效介电常数会随着外加电学条件的变化而变化[3], 其电容可调。同时,液晶的介电常数[4]、弹性常数[5-6]、挠曲电系数[7-9]和基板的锚定条件[10-11]等特性,对液晶盒电容特性及其液晶显示器件性能具有重要的影响。
液晶盒中的液晶分子呈楔形、纺锥形或香蕉形。当分子指向发生变化时,会引起整体结构的弯曲、展曲和扭曲等机械形变,此时存在显著的挠曲电效应。挠曲电效应描述了向列相液晶发生形变后液晶盒产生的自发极化现象,并具有永久的偶极矩[12-13],影响液晶盒的介电常数[7]。崔文静等基于液晶弹性理论和变分原理,推导了液晶盒系统的平衡态方程和电容的表达式,模拟不同挠曲电系数下电压-电容曲线,分析了液晶挠曲电特性对液晶盒电容的影响[8],以及弹性常数和介电各向异性对混合液晶盒和平行液晶盒电容的影响[14]。Kaur等[15]实验测试了液晶盒中液晶分子指向偏转的临界电压,获得了展曲和弯曲挠曲电系数的差值。Reshetnyak等[16]采用一种半定量的方法描述了光折变材料中两束光引起的能量增益,发现液晶的挠曲电能是驱动光栅结构的主要物理机制。Vitoriano和Satiro[17]考虑液晶盒中液晶分子不同的分布密度,分析了液晶分子指向密度耦合理论在实验测量挠曲电系数e3和e1以及组合e1+e3和e1-e3中的实际应用。
相场法可以模拟并预测材料在不同的物理场下各种微观结构的形成及演化过程。Oates和Wang[18]建立了向列相液晶的相场模型,研究了液晶中单畴和多畴结构,分析了热和机械拉伸加载过程中液晶核的自发形态和多畴结构的演化。液晶器件大部分是在电压控制下进行工作,如果液晶器件与其他电容器连接时,也可以在恒定表面电荷控制下工作。但是,关于采用相场方法研究各种初始取向液晶在表面电荷密度作用下液晶核指向的演化,并最终分析如何影响宏观电学特性的工作还很少见。
本文考虑构建研究液晶微结构的相场方法,结合液晶材料的挠曲电效应,应用液晶相整体的自由能密度,分析液晶指向矢随外加表面电荷密度的演化,并给出液晶盒约化电容离散化的表达式。通过数值算例,分析讨论混合液晶盒和平行液晶盒液晶指向矢、约化电容与挠曲电系数、机械约束条件、表面电荷密度和液晶盒厚度等的相互数值关系与演变趋势。
2 液晶系统的相场方法
2.1 液晶盒系统的自由能密度
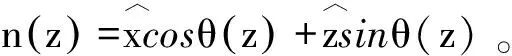
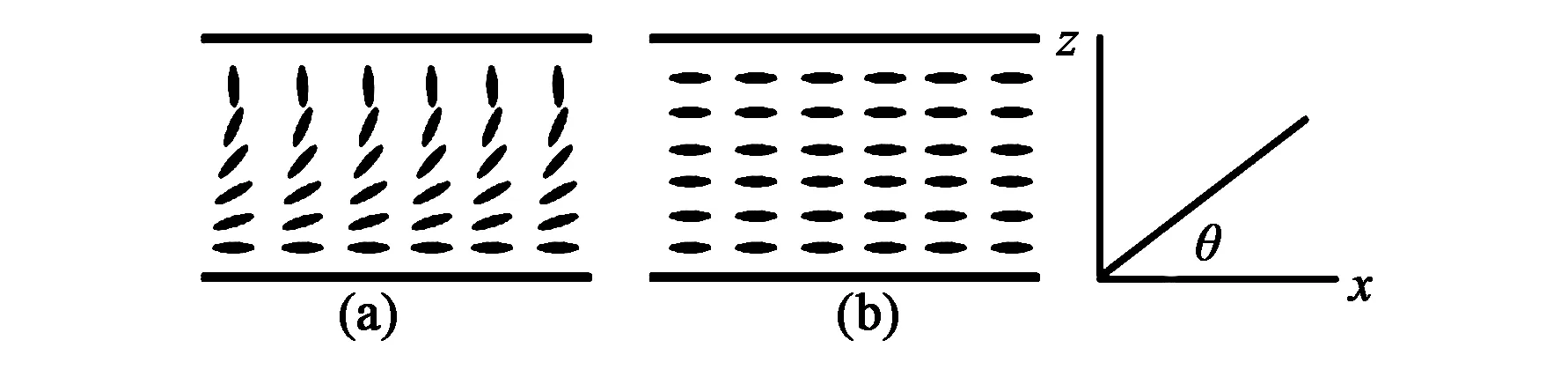
图1 混合液晶盒(a)和平行液晶盒(b)结构和坐标系Fig.1 Structure of liquid crystal cells and the coordinate system. (a) HAN cell, (b) PAN cell.
液晶盒的总自由能可以表示为[19]:
(1)
其中:fof、fdiel和fflex分别表示弹性形变自由能密度、介电自由能密度和挠曲电效应引起的自由能密度。弹性形变自由能的表达式为[20]:

(2)
其中:K1,K2和K3分别表示液晶的展曲、扭曲和弯曲弹性系数,为拉普拉斯算子。对于本文分析的一维问题,代入液晶指向矢n(z)可以得到形变自由能密度为:
(3)
式(3)中不存在含K2的项,说明在一维问题中液晶盒没有发生扭曲形变,只有展曲和弯曲形变。对于本文研究的对象,液晶的电位移矢量可以表示为:
D=ε0[ε⊥E+(Δε)(E·n)n]+Pf,
(4)
其中:ε0为真空介电常数,ε⊥为垂直于液晶分子长轴方向的相对介电常数,ε‖为平行于液晶分子长轴方向的相对介电常数,Δε=ε‖-ε⊥为液晶材料的介电各向异性。E表示液晶中的电场强度。Pf是液晶中由于挠曲电效应产生的极化强度[17]:
Pf=e1n(·n)+e3[(×n)×n],
(5)
其中:e1和e3表示液晶展曲和弯曲的挠曲电系数。对于一维问题,z方向上的极化强度Pfz可以表示为:
(6)
当液晶盒表面存在自由表面电荷密度σ时,可以获得液晶盒内沿厚度方向上的电场分布为[17]:
(7)
因此,液晶系统的介电自由能fdiel可以表示为:
(8)
而由于挠曲电效应引起的自由能为:
(9)
结合式(4,6,8,9)可以看出,液晶系统的自由能密度与液晶分子的指向矢即液晶核的极化方向密切相关。当外加物理场发生改变时,液晶分子通过改变其指向矢(极化方向)来降低系统的自由能,使得液晶盒系统更稳定。
2.2 液晶指向矢的相场方程
相场方法可以通过序参量模拟材料内部微结构的演化,也可以很容易推广描述二维和三维结构。本文把表示液晶分子指向矢的偏转角θ作为液晶系统的序参量,其在外场下的演化可以通过动态金兹堡-朗道方程来求解[21]:
(10)
其中:δF/δθ(r,t)表示热力学驱动力,t为时间,L为动力学系数。将式(1,3,8,9)代入式(10),得到关于液晶指向矢偏角θ的相场方程具体表达式:
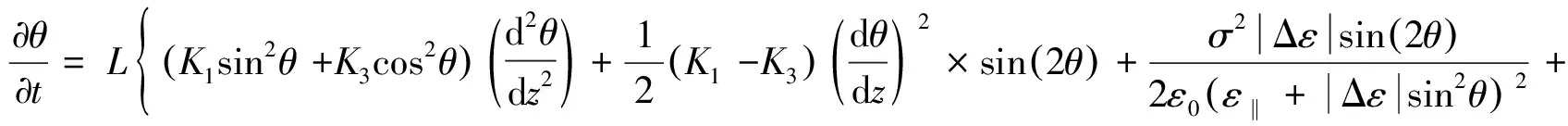
(11)
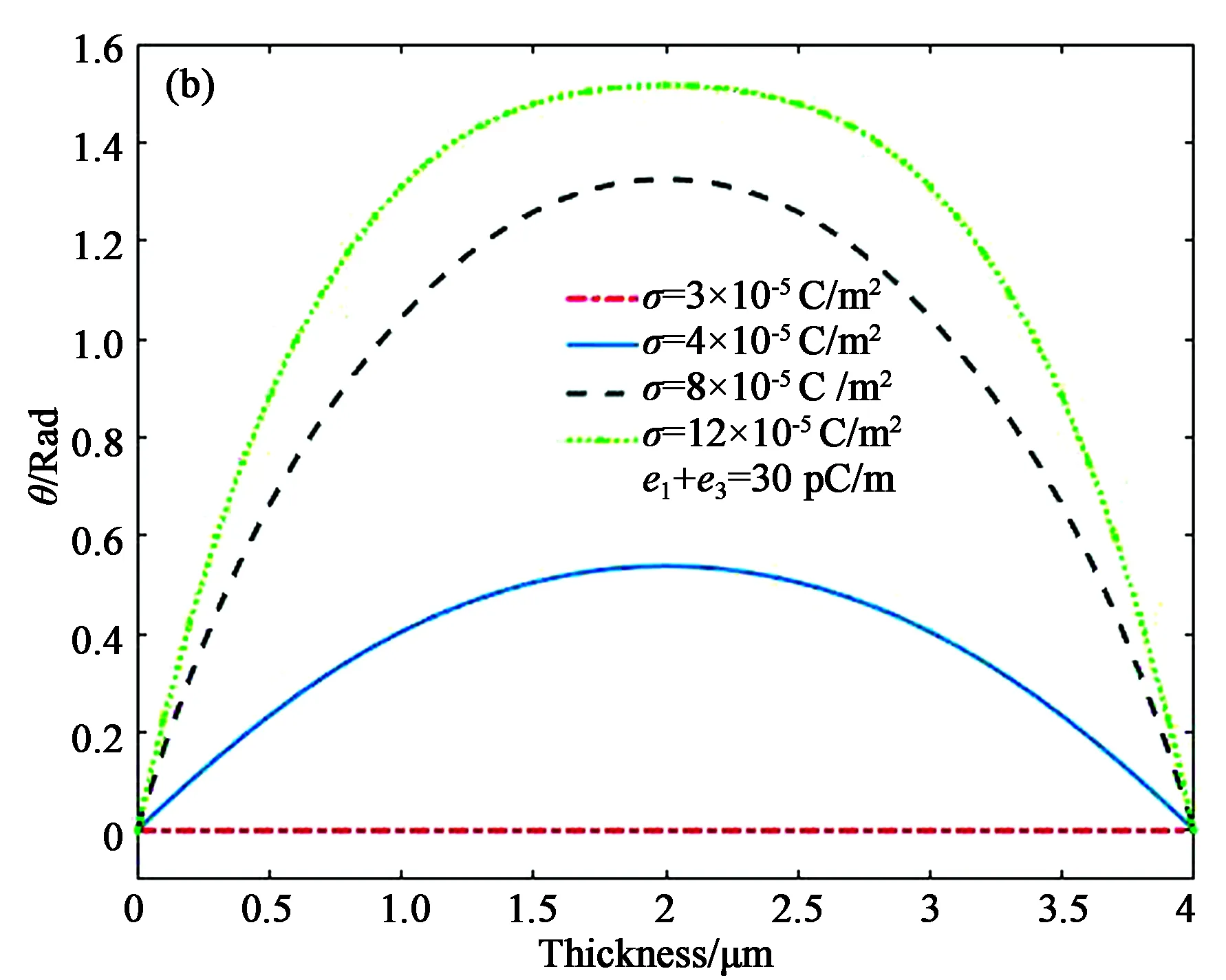
式(11)相场方程可以通过有限差分法求解。将液晶盒沿厚度方向平均划分成m份,在第i(1 (12) (13) (14) 将式(14)简化为如下函数形式: (15) (16) 其中: (17) 其中:Δt表示时间步长。 (18) (19) (20) 从式(20)可以看粗,约化电容与液晶盒内液晶分子指向分布密切相关。 在整个数值计算过程中,采用如下材料参数[8]:r=1、L=1、K1=6.2 pN、K3=8.3 pN、Δε=5.2、ε‖=10.5、ε0=8.85×10-12C2/(N·m2)。液晶盒厚度取d= 4μm,沿厚度方向分成10等份,即m=10,计算时间步长Δt=1×10-4,整个时间循环次数为5000~30 000。通过数值算例发现,对于平行液晶盒,在临界厚度或临界电荷密度工况下,时间循环次数需要达到30 000时结果才能趋于稳定值。在液晶盒上下基板位置上设定液晶核的机械边界条件,对于平行液晶盒θ(1)=θ(11)=0,而混合液晶盒θ(1)=0,θ(11)=/2,在液晶盒内每个节点液晶指向矢偏角的计算初始值赋予微小高斯随机值。 图2 不同表面电荷密度值对混合液晶盒(a)和平行液晶盒(b)指向矢厚度分布的影响Fig.2 Distribution of director in (a) HAN cell and (b) PAN cell with different surface charge density 图2给出了不同表面电荷对混合液晶盒与平行液晶盒内液晶分子指向矢分布的影响,此时挠曲电系数和取e1+e3=30 pC/m。从图2(a)中可以看出,在混合液晶盒中,表面电荷密度越大,液晶分子的指向矢偏角越大,沿厚度方向指向矢偏角在0~π/2连续变化。从图2(b)可以看出,在平行液晶盒中,当表面电荷密度超过某一临界值时(大约3×10-5C/m2),液晶分子指向矢才能发生改变,并在液晶盒中间层出现最大值。当表面电荷密度低于临界值时,液晶分子指向矢保持不变。临界表面电荷密度值与液晶盒的厚度密切相关,将在下节讨论。 图3 不同挠曲电系数对混合液晶盒(a)和平行液晶盒(b)指向矢厚度分布的影响Fig.3 Distribution of director in (a) HAN cell and (b) PAN cell with different flexoelectric coefficients 图3给出了挠曲电效应对两种液晶盒指向矢分布的影响,此时表面电荷密度取σ=8×10-5C/m2。从图中可以看出,在混合液晶盒和平行液晶盒中,挠曲电效应对液晶核指向矢的影响是一样的,即挠曲电系数和越大,液晶核指向矢偏角越小。这个结果与文献[7]报道的结果很类似,他们讨论的是电压控制。 图4 不同挠曲电系数对混合液晶盒(a)和平行液晶盒(b)约化电容-表面电荷密度曲线的影响Fig.4 Capacitance-surface charge density curve in (a) HAN and (b) PAN cell with different flexoelectric coefficients 图4分别给出了挠曲电效应对约化电容-表面电荷密度曲线的影响。从图4(a)可以发现,在混合液晶盒中,当表面电荷密度较小时,约化电容随表面电荷密度的增加而显著增加,当表面电荷密度较大时,约化电容趋于稳定值。这是因为在不断加大的表面电荷作用下,液晶分子指向矢都稳定地趋于电场的加载方向,因此约化电容的变化逐渐平缓并最终趋于稳定。而从图4(b)可以发现,在平行盒液晶盒中,当表面电荷密度低于临界值时,约化电容不发生改变,当表面电荷密度超过临界值时,液晶盒的约化电容发生陡变,并最终趋于稳定。这是因为,在平行液晶盒中,电荷密度达到临界值后,液晶分子指向矢发生变化,从而引起电容的巨大变化,而且平行液晶盒的液晶分子指向矢比混合液晶的液晶分子指向矢更快的达到饱和指向。图4也显示了在混合液晶盒和平行液晶盒中,挠曲电系数和越大,约化电容越小,但随着表面电荷密度的增加,约化电容最终会趋于相等。因此,我们可以通过调节液晶材料的挠曲电系数来调控液晶盒的宏观电容特性。 图5 不同挠曲电系数对(a)混合液晶盒和(b)平行液晶盒约化电容-厚度曲线的影响Fig.5 Capacitance-Thickness in (a) HAN and (b) PAN cell with different flexoelectric coefficients 图5给出了两种液晶盒中挠曲电效应对约化电容-厚度关系曲线的影响,此时表面电荷密度取σ=8×10-5C/m2。图5(a)显示,在混合液晶盒中,当表面电荷密度确定时,约化电容随着液晶盒厚度的增加而增加。当液晶盒厚度达到一定值时,约化电容趋于稳定。从图5(b)可以看出,在平行液晶盒中,当表面电荷确定时,液晶厚度存在一临界值,当液晶盒厚度小于此临界值时,约化电容保持不变;当液晶盒厚度达到此临界值时,电容发生陡增并很快达到稳定值。因此,当设计液晶器件时,需要充分考虑其应用工况。例如,当工况表面电荷密度确定时,设计平行液晶盒的厚度必须大于临界厚度,这样才能获得大的电容特性。从图5(b)也可以看出,挠曲电效应对液晶盒厚度临界值几乎无影响。 图6 不同表面电荷密度对(a)混合液晶盒和(b)平行液晶盒约化电容-厚度曲线的影响Fig.6 Capacitance-Thickness curve in (a) HAN and (b) PAN cell with different surface free charge density 图6分别给出了两种液晶盒中表面电荷密度对约化电容-厚度关系的影响,此时挠曲电效应取e1+e3=30 pC/m。从图6(a)中可以看出,大的表面电荷密度产生更大的约化电容,但是,表面电荷密度大小对大厚度的液晶盒几乎无影响。而图6(b)的结果显示,在平行液晶盒中,表面电荷密度越大,液晶盒的约化电容发生改变时的液晶盒厚度越小,即液晶分子发生反转时的临界厚度越小。因此,当设计应用于小表面电荷密度工况下工作的平行液晶盒时,液晶盒的厚度应该尽量小。图6(b)也显示,对于大厚度液晶盒,表面电荷密度也几乎不改变液晶盒的约化电容。 本文采用相场方法研究了表面电荷作用下不同初始分布向列相液晶盒(混合液晶盒与平行液晶盒)中挠曲电效应对液晶电容特性的影响。基于液晶盒的整体能量,构建描述液晶分子指向矢偏角在外加电场下演化的相场方程,给出了液晶盒约化电容的数值表达式。分析了挠曲电系数和表面电荷密度对混合液晶盒和平行液晶核指向矢的影响,讨论了两种初始分布的液晶盒内约化电容-表面电荷密度曲线和约化电容-厚度曲线。分析结果表明,在混合液晶盒中,表面电荷密度越大,挠曲电系数越小,液晶核指向矢偏角越大并最终沿电荷加载的方向趋于稳定,其约化电容随表面电荷和液晶厚度的增加而增加并趋于平缓。在平行液晶盒中,表面电荷密度和液晶厚度都存在临界值,当超过其临界值时,液晶核的指向矢才会发生偏转,从而引起液晶电容的巨大改变。当表面电荷密度越大,液晶盒约化电容发生显著变化的临界厚度越小,而表面电荷密度几乎不影响大厚度液晶盒的约化电容。因而,液晶器件在设计时应该充分考虑其应用工况(表面电荷密度)、液晶盒厚度、液晶核初始取向与液晶材料等各种因素的影响。


2.3 液晶盒电容表达式
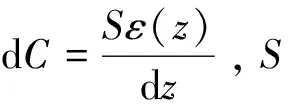
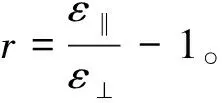
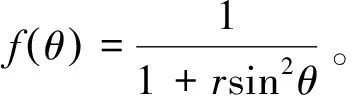
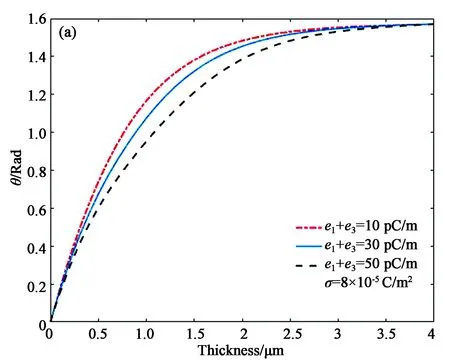
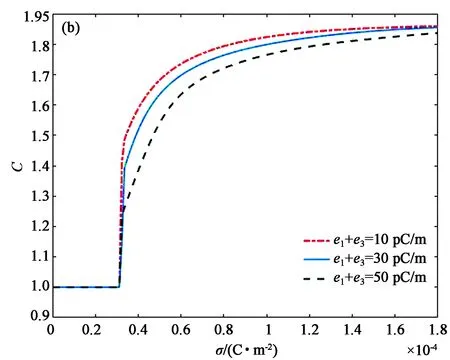
3 数值分析与讨论







4 结 论

