基于复杂网络的南京城市轨道交通站点重要度评估

吴 桐 徐永能（南京理工大学自动化学院，南京 210094）

引言

随着城市化进程的迅速推进以及城市人口的快速增长，越来越多的大都市形成了网络化的城市轨道交通网。城市轨道交通建设投资巨大，是一项有巨大影响力的民生工程，针对城市轨道交通的网络特性开展研究，对城市轨道交通的规划和运营都具有重要的意义。城市轨道交通在运营过程中其路网经常会受到各种突发事件的干扰，包括外界突发事件（如人为破坏、自然灾害等）、人工操作失误、设备系统故障等等，这些突发事件均会在不同程度上对城市轨道交通线网造成影响，导致线网的局部失效，甚至引发连锁反应，对整个城市轨道交通线网运营造成巨大的影响。由于大都市的城市轨道交通都已经实现网络化运营，可以利用复杂网络理论对其进行研究。

大多数关于城市轨道交通网络的研究都只从模型的角度阐述了点或边失效后对整个网络结构的影响，而从城市轨道交通实际运营的角度来看，站点的位置、客流量、站点的特点都会对整个城市轨道交通网络产生重要影响，因此城市轨道交通网络节点重要度评估应该有更为丰富的评价体系。

1 城市轨道交通复杂网络理论基础

1.1 复杂网络的统计特征

（1）度与介数。节点vi的度ki指的是与节点vi相连的节点或者边的数目，一般来讲在网络中与该节点相连的节点或者边的数目越多，该节点就拥有越大的度值[1]。

节点的介数Bi一般用来表示节点在网络中的重要程度，定义为网络中所有穿过节点vi最短路径的数量σij（vi）与网络中所有最短路径的数量σij的比值。

（2）平均路径长度。不同节点vi和vj之间的距离dij是这两个节点之间最短路径的边数，网络平均路径长度L为网络中不同节点之间的平均距离[2-3]。

式中，N表示城市轨道交通网络中节点的总数。

（3）聚类系数。聚类系数一般用来说明网络内不同节点的聚集程度，节点vi的聚类系数一般用Ci表示，指的是一定范围内ki个节点之间存在的边数Ei和理论边数之比。

（4）特征向量。在复杂网络中，特征向量是一个节点重要性的度量，指的是网络中的每一个节点都有一个相对的指数值，其中高指数节点的连接对一个节点的贡献度要比低指数节点的贡献度高。简单来讲，度是从节点本身连接节点数量的多少来评价其重要性，但在生活中某些节点本身的度值很小，但却是局部网络之间的连接点，此时这个节点的作用就变得十分重要，因此评估节点的重要性除了考虑其本身连接节点的数量之外，还要考虑其连接节点的“质量”。特征向量这一指标重点考虑了相邻节点重要性对节点重要性的影响，也就是说一个节点的重要性为其相邻节点的重要性之和[4-6]。

1.2 城市轨道交通复杂网络模型

在城市道路交通网络中，对偶法和原始法是两种常用的建模方法，对偶法是把交叉口抽象为边，道路抽象为节点，而原始法则相反。因为城市轨道交通网络中存在换乘站点，所以城市轨道交通网络的建模方法与城市道路交通有所差异，城市轨道交通网络的建模方法主要有SpaceL、SpaceR和SpaceP 方法[7-10]。

SpaceL方法是将城市轨道交通网络中的站点抽象为节点，相邻站点之间的线路抽象为边，构建的网络为城市轨道交通的自然拓扑结构，这种结构有助分析路网最基本的特征和路段的特性；SpaceR方法是将网络中的线路抽象为节点，若线路之间存在换乘站点，则这两条线路之间就存在一条边，这种结构可以体现线路之间的换乘站点数目以及换乘的难易程度；SpaceP方法是将城市轨道交通网络中的站点抽象为节点，然后将同一条线路中的所有站点两两相连，这种结构有利于体现不同线路之间的换乘现象。

基于以上城市轨道交通复杂网络建模方法，结合本文的研究内容和城市轨道交通网络特点，选取SpaceL方法来构建城市轨道交通复杂网络模型。原因如下：

（1）SpaceL方法构建的网络规模更大，节点更多，结构更复杂，可以更直观地反映实际网络的规模与结构复杂程度。

（2）SpaceR和SpaceP方法主要根据网络连边考虑网络的换乘关系，而SpaceL方法可以更好地反映网络节点的特性，展示出城市轨道交通的自然网络形态结构。

2 南京城市轨道交通站点重要度评估

在城市轨道交通网络中一旦站点发生紧急事件，会对城市轨道交通网络的联通性产生巨大的影响，因此对网络节点进行重要度评估有很大的现实意义。不但可以增强城市轨道交通网络的连通可靠性，还可以为预防交通拥堵、加强交通管理提供一定的参考，为城市居民提供合适的出行方案。

截至2018年6月，南京地铁共建成10条运营线路，包括1、2、3、4、10、S1、S3、S7、S8及S9号线，共174座车站，地铁线路总长378千米，南京地铁网络化运营的格局已初步形成，本文将车站逐一编号，构建相应的网络拓扑图（图1）。

图2 网络节点重要度评估指标体系

图1 南京地铁网络拓扑图

2.1 南京城市轨道交通站点重要度评估指标体系

目前对城市轨道交通网络中节点重要度的分析主要是从节点本身的固有属性去考虑节点在网络中的重要性，而城市轨道交通作为城市中人们日常出行的重要载体，每个站点由于其区位的不同，日均客流量会有着很大的差异，这也是节点在网络中重要性的一大体现。本文基于对城市轨道交通网络静态特征指标进行分析的前提下，增加了客流指标，以此综合评估节点在城市轨道交通网络中的重要度，建立评价指标体系如图2所示。

（1）度值和介数。站点的度值指的是与该站点直接相连的车站个数，体现了该站点与其他站点之间联系的紧密性。在城市轨道交通网络中，通常换乘站的度值较高，站点的度值越高，在该站点换乘的线路就越多，也就意味着该站点对整个城市轨道交通网络有着更巨大的影响力。

与站点的度值有着相似的意义，站点的介数可以反映站点在整个城市轨道交通网络内的重要度，一般情况下通过站点的最短路径数目越多，该站点就越重要。南京地铁各车站度值与介数如图3、图4所示。

从图3、图4中可以看出，城市轨道交通网络中换乘站点拥有着较大的度值，换乘线路越多的站点度值越高，而大部分的站点度值都为2，这一现象符合城市轨道交通网络的基本特征。与度值类似，介数较高的车站都为轨道交通网络中换乘站，表明人们在日常出行当中，更多的会经过这些站点，这些换乘站在人们的日常出行线路中占着更高的比例，这与人们的现实出行状况相符。

（2）聚类系数。实际上许多大规模的网络都具有聚类效应，即网络局部区域节点会趋向于集中。在城市轨道交通网络中，站点的设置受城市规划布局的影响，轨道交通站点会明显聚集在市中心以及重要交通节点等区域，在局部地区站点的密集度会明显增大，区域内站点的聚类系数也会相对较高。

但受城市轨道交通网络本身结构特征的影响，很少有车站之间能够组成三元组，所以大多数节点的聚类系数都为0，整个网络的聚类系数也大都为0，从这点可以看出城市轨道交通网络是一个较为稀疏的网络。

图3 南京地铁各车站度值

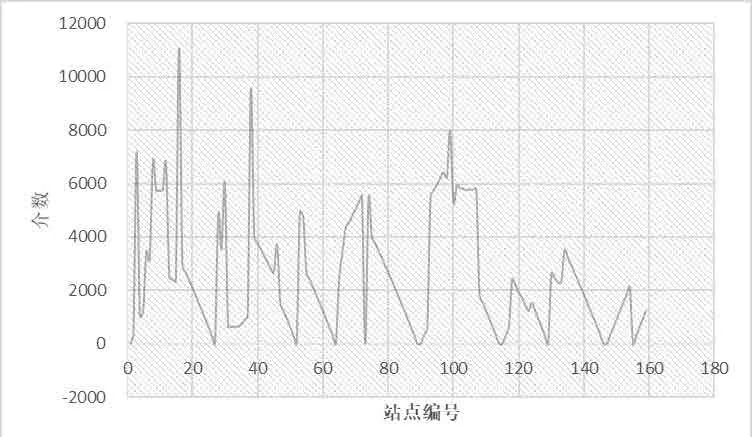
图4 南京地铁各车站介数

（3）特征向量。在复杂网络中，特征向量是利用相邻节点的重要性之和去评价该节点的重要性的。在城市轨道交通网络中，当站点连接某些重要站点比如换乘站时，此站点的特征向量值就会比较高。在现实生活中，一般来讲一个站点越靠近换乘站，当它受损时对换乘站的影响就越大，并且该站点的客流相比其他站点也更为密集，换而言之该站点的重要性也就越高[11-13]。南京地铁各车站特征向量如图5所示。

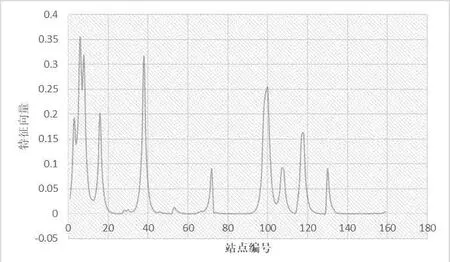
图5 南京地铁各车站特征向量

可以明显看出特征向量高的车站都集中在换乘站的周围，这是由于换乘站通常是不同线路组团的中介节点，所以换乘站周围的节点包括换乘站在内的相邻节点都有着很高的重要性。

（4）客流指标。城市轨道交通站点的类别有首末站、中间站、换乘站等，每一个站点由于其地理位置、承担功能的不同，其日均客流量会有很大的差异。日均客流量越大的站点，在路网中就有着越重要的地位，一旦节点失效，对城市轨道交通运营会产生更大的影响。因此本文利用节点的日均客流量作为城市轨道交通路网的客流评价指标。南京地铁各车站2018年日均客流量如图6所示。

图6 南京地铁各车站日均客流

可以看出换乘站及其相邻站点的客流量会明显增多，并且1、2号线的客流量明显大于其他新开线路的客流量。

2.2 南京城市轨道交通站点重要度评估模型

2.2.1 指标权重的确立

指标权重的合理性对最终评估结果会有很大的影响，在对城市轨道交通网络节点重要度进行综合评估时，各项指标的权重体现了其在整个指标体系中的重要性。在以往的研究中，确定权重系数的方法一般有主观赋值法和客观赋值法两类，考虑到此次研究对象为城市轨道交通网络，在评估时不建议加入主观意见，因此本文利用客观赋值法中的变异系数法来确定不同指标的权重。

变异系数法的基本原理为：评价过程中的各项指标数据差异越大，就越能表达出更多的信息，进而体现设立不同指标之间的差异，然后对数据差异比较大的指标赋予比较高的权重。本文依据变异系数法计算城市轨道交通网络节点重要度指标权重的基本步骤如下：

（1）建立评价矩阵。本文的网络节点重要度综合评估指标体系共有5个指标，假设网络中共有n个节点，根据各指标计算得到数据建立评价矩阵：

其中，xij指的是第i个节点的第j个指标值。

（2）计算标准差。由于本文构建的5个评价指标均为正向指标，因此不需要对指标进行同向化处理，标准差的计算公式为：

（3）计算各指标的变异系数。变异系数计算公式为：

（4）变异系数归一化处理。在计算过程中，各指标数据的量纲和数量级有很大的差异，对变异系数进行归一化处理可以对评价结果进行统一衡量，然后将归一化处理后的数值作为各指标的权重，权重计算公式为：

通过计算得到南京地铁网络特性指标权重见表1。

表1 南京地铁网络特性指标权重

2.2.2 网络节点重要度综合评估

网络综合评价方法不胜枚举，由于TOPSIS方法评估结果相对客观，可以较为充分地利用现有数据信息，合理反映出评价对象的整体情况，并具有广泛的适用性，因此本文采用TOPSIS方法对城市轨道交通网络节点综合重要度进行评估。

基于TOPSIS方法的城市轨道交通网络节点综合重要度排序计算步骤如下：

（1）构造决策矩阵。本文在网络节点重要度综合评估指标体系共有5个指标，假设网络中共有n个节点，所有节点的指标值构成基本决策矩阵如下：

其中，xij指的是第i个节点的第j个指标值。

（2）计算规范化决策矩阵。将基本决策矩阵进行规范化处理：

（3）构造权重规范化矩阵。根据上一节中得到的各指标的权重矩阵W=[W1，W2，W3，W4，W5]，将规范化矩阵的第j列乘以其权重Wj得到权重规范化矩阵：

（4）确定正负理想解。正理想解：

负理想解：

（5）计算各节点指标到正负理想解的距离。到正理想解的距离：

到负理想解的距离：

（6）计算各节点指标和理想解的接近程度。节点与理想解的接近程度为：

式中fi的值越大，节点的重要度越高。

（7）根据接近程度对节点重要度进行排序。

基于上述步骤，将城市轨道交通站点按照节点与理想解的接近程度由大到小进行排序，就可以得到城市轨道交通站点的重要度排序。

经计算得到南京地铁站点重要度排序见表2（仅显示前50个站点）。

根据南京市城市轨道交通网络节点重要度的评估结果，由车站排名分析可得出以下结论：

表2 南京地铁站点重要度排序

（1）网络中重要度较高的节点大多数为网络中的换乘站，例如新街口、南京南站、南京站、鼓楼、大行宫等车站，这类车站在网络中拥有着较大的连接数，度值较高，具有较高的局部重要性。其次换乘站往往会汇聚大量的乘客，乘客通过换乘站换乘到其他线路，因此大部分乘客出行会经过这些关键车站，所以这些换乘站同时也拥有较高的介数，具有较高的全局重要性。当网络中移除这些连接线路较多、客流量较大的车站时对网络的连通性和功能影响较大，因此这些重要换乘站是网络中的关键车站。

（2）城市轨道交通网络初期及中期建设的线路上的车站重要度高于近期建设的轨道交通线路车站，这些重要度高的车站分布在1、2号线上。其主要原因是由于南京市轨道交通网络为无标度网络，随着轨道交通网络规模的扩大，新建线路上的节点更倾向于与初期建设的线路上的节点相连，使得这些节点具有较多的连接线路，在网络中这些节点的吸引力大于其他节点，因此这些节点的重要程度更高。

3 结语

在对城市轨道交通网络节点进行重要度评估时，不仅仅需要从网络拓扑结构的角度去考虑不同节点在整个网络中的重要程度，站点的位置、客流量、站点的特点都会影响到站点在整个城市轨道交通网络中的重要性，需要从更全面的角度去对城市轨道交通站点的重要度进行分析。本文基于网络节点性、网络全局性和客流三方面来设立相应的评价指标，既考虑到了城市轨道交通的复杂网络特性，又顾全了城市轨道交通运营站点客流差异较大这一特点，在以往研究的基础上建立了更全面的城市轨道交通站点重要度综合评估模型，具有一定的参考价值。