氢气在微燃烧器内的能源转化

张文珺，陈 威

（苏州大学能源学院，江苏苏州215000）

随着环境污染和化石能源资源的快速减少，对高效、清洁燃烧技术的需求越来越迫切[1]608。与常规燃烧相比，微燃烧器是一种体积小于1cm3的微型燃烧装置[2]23。微燃烧器是微动力系统的重要组成部分，其功能是通过燃料在微燃烧器中的燃烧反应和传热过程，将燃料的化学能转化为热能和动能，再通过热辐射装置将其转化为电能。微尺度燃烧是随着微机电系统（MEMS）技术的发展而提出的，目前，微型燃气轮机的功率可达10～100 W，体积仅为1 cm3，每小时耗油约7 g，如果进一步发展，其能量密度将是目前最佳电池的10倍以上[2]24。

碳氢燃料用于微型燃烧驱动的动力源，其能量密度远高于电池（100倍）[3]。碳氢化合物的比能量极高（通常为45 MJ/kg），而目前可用的顶级电池（锂）的能量密度为1.2 MJ/kg，即使微型发动机的热效率约为4%，其输出功率也比电池的功率大，这是微型发动机发展超微型燃烧器的动力[4]3067。蒋等人研发了燃烧甲烷/空气混合物[5]和二甲醚/空气混合物[6]596的平面火焰微燃烧器及其温差热电转化系统。

微动力系统很有前景，但其主要问题是如何在微燃烧器中实现可持续燃烧。随着燃烧室尺寸的减小，表面积与体积比增大，燃料在燃烧室内停留时间短，导致燃烧室的热损失增大，燃烧不稳定[7]353。Li等人[8]建立了一维火焰模型，对圆柱形微燃烧室的传热过程进行了分析。Sakurai等人[4]3068研究的平焰超微型燃烧器能够有效地利用燃烧气体与预混料之间的热循环，稳定火焰，减少热损失，提高空间加热率。预混火焰有利于降低热损失和提高火焰稳定性[9]。刘伟等人[10]建立了Swiss-roll型微燃烧器的燃烧模型，采用FLUENT软件对微燃烧器中甲烷/空气的燃烧特性进行了数值模拟，研究了甲烷/氧气的当量比为1时，流速不同对微燃烧器内燃烧的影响。Zhong等人[11]比较了不同流量、不同当量比和壁材的微管的燃烧现象和热损失。研究发现当当量比为1时，燃烧释放热量、热损失和壁温均达到峰值。Fanaee等人[12]建立了在不同壁温值下变反应区厚度的二维模型，对微燃烧室的催化/非催化燃烧现象进行了分析研究。结果得出催化条件的火焰温度比非催化条件下的火焰温度低，热损失和热应力问题减少。

在微燃烧器的研究中，多孔介质帮助稳燃也是一个方向。Xu等人[1]609利用二维双温度模型对超贫燃烧过程进行了数值模拟。结果发现，采用多孔介质，扩大了自组织稳定燃烧的当量比范围。同时一种微型平板火焰矩形燃烧器也被用来验证微燃烧器采用多孔壁面作为混合气入口可以降低壁面温度和热损失[6]597。用多孔介质（如碳化硅）填充微燃烧器可显著提高壁面温度，从而提高微燃烧器的有效辐射能。但是孔隙度过大或过小都会削弱燃烧过程[13]。

微燃烧器的结构也是一个研究方向。Leach等人[14]建立了微通道内反应流动的一维数值模型，以确定微燃烧器的最佳结构。Benedetto等人[15]采用三维计算流体力学（CFD）模拟方法，发现方形截面微燃烧器比圆形截面具有更强的抗消光能力，这是由于墙角产生的热点所致。同时钝体形状对平面微燃烧器爆炸极限的影响也被研究，得出在当量比为0.5时，三角钝体燃烧室和半圆钝体燃烧室的爆炸极限分别为36 m/s和43 m/s左右[16]。Yang等人[17]发现壁厚为0.4 mm的微型TPV发电机的性能最好，改进壁材（如使用碳化硅[18]）也可以提高燃烧器的热性能。

Chen等人[7]349利用Fortran程序建立一维数值模型，探讨带有余热回收的微燃烧器中甲烷/空气燃烧的可行性，并讨论了其在TPV动力系统中的应用。本文正是基于此种方法，用MATLAB程序建立了带有余热回收的微燃烧器的一维数值模型，探讨微燃烧器中氢气在空气和纯氧条件下的燃烧特性，研究了当量比、内管直径和进气速度对微燃烧器燃烧性能的影响，计算了热光伏系统中化学能转化为电能的能量转化效率，比较了氢气在空气和纯氧状态下的淬火直径和稀燃极限。

1 数值模拟及其公式

1.1 微燃烧器的物理模型

图1为本研究中使用的开口系统微燃烧器的物理模型，与Chen等人[7]349使用的模型类似。它包括直径为1～3 mm的燃烧管和用作逆流换热器的同心外管。外管内的高温气体可以预热内管的冷预混燃料混合物，可燃混合气在内管中的某一点达到着火温度，火焰接着扩散到其他各处，实现能量的传递。燃料和空气在同心圆管（Burke-Schumann[BS]火焰）的燃烧将首先作为一个扩散限制的现象来处理，然后扩展到合流空气中[19]。由于火焰尺寸的减小，火焰变得不太稳定，并且由于火焰对燃烧室壁面的热损失、气体壁面活性组分的破坏和停留时间的缩短，火焰趋于熄灭，使得系统的效率相对较低[20]，但是具有热恢复作用的燃烧室壁面的温度分布要高于无热恢复的燃烧室壁面的温度分布[21]，热回收有助于微燃烧室在较小尺度上维持燃烧。

图1 微燃烧器的理论模型

1.2 微燃烧器的传热计算

在计算外管的对流换热系数时，用到了Nu。内壁温度的经验关联式确定了内管的Nu[22]，Nu表示壁面上流体的无量纲温度梯度：

式中：hinner为对流传热系数，W·m-2·K-1；di为内管直径，mm；k为流体的导热系数，W·m-1·K-1。无量纲的Bi表征了在固体体内的传热阻力，指固体内部导热热阻与界面上换热热阻之比，它被定义为[23]

式中：Lc为特征长度，mm。这种经验公式适用于圆管中的强制对流层流。当微燃烧器足够小时，Bi接近于零，这相当于111 W·m-2·K-1的传热系数[24]。所以管壁的Nu为4.364，由此可以计算出管壁的传热系数。

1.3 微燃烧器内可燃混合气的燃烧过程

氢气在燃烧过程中的消耗率(ẇF‴)公式与甲烷的类似：

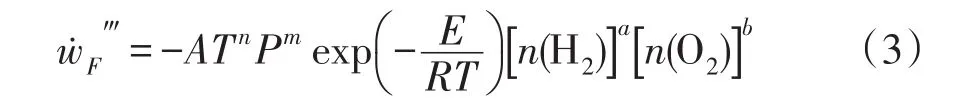
式中：a=1，b=0.5，n=0，m=0；A 是指前因子，是无量纲数，这里等于1.8×1018；T表示温度，K；P表示一个大气压，101 325 kPa；E表示氢气的活化能，这里等于146 422 kJ·kmol-1；R是理想气体常数；[n(H2)]和[n(O2)]分别是以kmol·m-3为单位的H2和O2的浓度。

燃料和氧气的质量守恒方程建立如下[7]350：

式中：ρ为气体密度，kg/m3；u为气体流速，m/s；D为扩散系数，m2/s；yF为燃料质量分数，%；y1为空气-燃料混合物中的氧气质量分数，%；为氧气消耗率。

在上述假设的基础上，将流体流场划分为有限个小的控制量，如图2所示。燃料和氧气的能量守恒方程建立如下：

图2是内管开口系的能量守恒图：

图2 内管开口系的能量守恒[7]

式（7）和式（8）分别表示内外管的燃烧过程和传热过程[7]351，由此可以得出微燃烧器外管壁温：

式中：cp是气体的定压比热容，J/（kg·K）；Ai是内管的交叉面积，mm2；Ao是外管的交叉面积，mm2；hH是内管换热系数，W·m-2·K-1；hH,outer,o是外管换热系数，W·m-2·K-1；Ci是内管湿周，mm；Co是外管湿周，mm；hc是氢气的摩尔燃烧焓，J/kg；Tg,o和Tg,i是内管壁温，K；T是可燃混合气的温度，K；Tw,1是外管壁温，K。

通过公式（8）可以确定用作辐射源的气体和壁内外表面的温度。

1.4 微型TPV系统模型

图3是一种典型的利用燃烧热作为辐射源的TPV系统。该系统由两个主要部件组成：微燃烧器和热光电转换器。燃料在微燃烧器中燃烧，通过光伏电池从燃烧器吸收热辐射产生电能。为了确定光谱发射率，需要计算沿外管外表面的壁温[7]352。由普朗克辐射定律给出黑体半球发射功率[25]：

式中：λ为波长，m；C1=3.742×10-16W·m2，C2=1.4388×10-2m·K。

图3 微型TPV系统[25]

通过TPV系统可以将燃料燃烧释放的热能转化为电能。

2 结果与讨论

2.1 淬火直径

2.1.1 当量比对淬火直径的影响

式中：A为空气的摩尔数，mol；F为燃料的摩尔数，mol。

图4表示了氢气在空气和纯氧状态下，淬火直径随当量比的变化关系。在两种状态下，随着当量比的增加，淬火直径均先减小后增大。氢气在纯氧状态下的淬火直径比相同当量比条件下的空气状态下的淬火直径要小。当当量比为1时，氢气在纯氧下的淬火直径最小值（0.065 mm）比在空气中的最小值（0.1 mm）小。随着当量比的增加，燃料的质量分数增加，燃料燃烧释放出更多的化学能，导致火焰温度升高。火焰温度越高，化学反应速度越快，温度梯度越大。所以当当量比小于1时，淬火直径随当量比的增加而减小。当当量比大于1时，可燃混合气中所含实际空气量少于所必需的理论空气量，即空气量不足，当量比越大，燃料的质量分数越小，化学能释放不足，这就导致淬火直径增大。相同当量比条件下，纯氧中的氧气含量大于空气中的氧气含量，氢气燃烧得更充分，淬火直径相应减小。

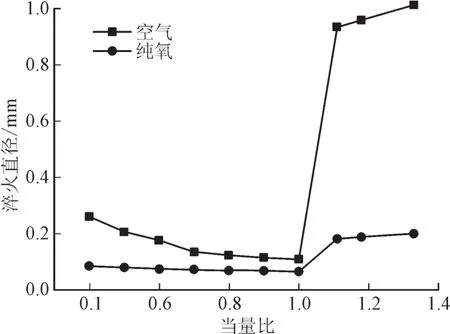
图4 氢气在空气和纯氧状态下不同当量比的淬火直径

2.1.2 进气速度对淬火直径的影响

在计算进气速度与淬火直径的关系时，考虑了Da。Da为停留时间和化学反应时间之比，为了保持管内的稳定燃烧，必须有比化学反应时间tfy更长的燃料停留时间ttl：

式中：L为燃烧室的长度，mm；u为气体流速，m/s；ρ为气体密度，kg/m3。对于微燃烧器，由于气体流速相对较高，管长较短，停留时间较短。化学反应时间与燃料的消耗率成反比关系。在本文的模型中，回收的余热增加了反应物的温度，从而提高了燃料的消耗率，缩短了化学反应时间。为了在管道内保持稳定燃烧，燃料停留时间要比化学反应时间更长。所以高的进气速度需要更大的管径来维持管内燃烧。

图5说明了可燃混合气进口速度与淬火直径的关系。当速度小于2 m·s-1时，提高进气速度，进入微燃烧室的燃料量会增多，增加燃料消耗率，导致淬火直径减小；当速度大于2 m·s-1时，由于停留时间的缩短，火焰向内管末端推进，燃料还未来得及反应就从燃烧室内流出，导致化学能释放减少，因此需要一个更大的淬火直径来稳定燃烧。

图5 氢气在空气和纯氧状态下不同进气速度的淬火直径

2.2 稀燃极限

在空气/燃料（称为可燃性极限）的某些值下，发热量不足以克服热损失，火焰也不会传播。图6展示了氢气在空气和纯氧状态下，进气速度为1 m·s-1时，不同内管直径的微燃烧室的稀燃极限。在两种状态下，氢气的稀燃极限均随内管直径的增大而减小。当当量比为1，内管直径在1～5 mm时，氢气在空气中的稀燃极限要比在纯氧中的稀燃极限低2%左右。

2.3 能量转化效率

2.3.1 传热系数对能量转化效率的影响

在TPV系统中，热能转化为电能是通过覆盖在微燃烧器外表面的热光伏电池来吸收热辐射的，其能量转换效率定义为

式中：E1为产生的电能，E2为输入的化学能。

图6 氢气在空气和纯氧状态下不同直径的稀燃极限

图7表示了氢气在空气和纯氧状态下燃烧时的能量转化效率随传热系数的变化关系。随着传热系数的增加，热循环越大，能量转化效率越高。通过增加传热系数，可获得更宽的火焰可燃性和较小的淬火直径。

图7 氢气在空气和纯氧状态下不同传热系数的能量转化效率

2.3.2 内管直径对能量转化效率的影响

图8表明进气速度为1 m·s-1的可燃混合气在不同内径的微燃烧器中燃烧时的能量转化效率。氢气在空气条件下，当内径为0.5 mm时，最高的效率为1.6%。氢气在纯氧条件下，当内径为0.5 mm时，最高的效率为6.3%。这个结果与Chen等人[7]351得出的规律类似。以氢气在空气状态下燃烧为例，当内管直径小于2 mm或者大于4.5 mm时，表面积与体积比减小在热辐射中占主导地位，导致效率下降，当直径从2 mm增加到4.5 mm时，壁面温度的升高主导着热辐射，从而导致效率的提高。

图8 氢气在空气和纯氧下不同直径的能量转化效率

3 结论

本文建立了氢气/空气（纯氧）在带有余热回收的微燃烧器中燃烧的理论模型，并对TPV系统的能量转化效率进行了评价：

（1）相同当量比条件下，氢气在空气中的淬火直径大于纯氧中的淬火直径。当当量比为1时，氢气在纯氧下的淬火直径最小值（0.065 mm）比在空气中的最小值（0.1 mm）小。

（2）随着进气速度的增加，淬火直径先减小后增大，与停留时间、反应时间有关。

（3）气体与壁面间较高的传热系数增强了热循环，提高了能量转化效率，可获得更高的火焰可燃性和较小的淬火直径。

（4）微燃烧器的表面积与体积比和壁面温度是影响总能量转化效率的重要参数。氢气在空气条件下，当内径为0.5 mm时，最高的效率为1.6%；氢气在纯氧条件下，当内径为0.5 mm时，最高的效率为6.3%。