基于生产运行数据的RH真空精炼装置可靠性分析

刘向东，姜玖辉，杨军波

（中冶赛迪技术研究中心有限公司，重庆401122）

评价可修复设备的可靠性常用平均故障间隔时间、平均维修时间和固有可用度等指标来衡量，需要有设备运行状况的实时记录。许多流程工业虽然实时记录了海量的生产运行数据，但往往并不包含与可靠性指标直接相关的基础数据，导致设备的可靠性评价和制定设备维护计划常常难以获得可信的理论计算依据。

流程工业是指生产连续不间断或半连续批量生产的工业过程，钢铁冶金生产是典型的流程工业。RH真空精炼装置是现代冶金技术实现大规模生产高品质钢铁产品的必备装备，主要由真空抽气系统、真空槽系统、顶枪系统、钢包顶升系统等设备组成。其冶金工艺利用了钢液中的气体在不同的分压下具有不同溶解度的原理，通过真空抽气系统使钢液的表面压力低于大气压，从而使钢液中的有害气体（主要是氢气）从钢液中溢出，减少钢液中有害气体的含量，进而提高钢铁产品的品质。RH真空精炼装置的使用特点是将真空槽的两只浸渍管插入钢水包的钢液里，通过真空抽气系统对真空槽抽气，使部分钢液在大气压力的作用下进入真空槽产生脱气反应，并在其中一只浸渍管下部通入惰性气体带动钢包内的钢液继续不断进入真空槽，而脱气后的钢液则通过另一只浸渍管回到钢水包，并与钢包内的钢液搅拌混和，再次被吸入真空槽，从而实现循环脱气。在此基础上，利用顶枪吹氧技术，实现真空下的碳氧反应进而除去钢液中的碳，得到低碳钢和超低碳钢；或者在加入铝粒的同时吹氧，使铝氧反应产生热量对钢液升温；或者喷入脱硫粉剂降低硫含量，获得高品质钢[1]。在两次真空处理间隙，需要用顶枪对真空槽加热烘烤和化冷钢，并对真空槽的浸渍管进行除渣和喷补维护。在真空槽耐材寿命到期后，需要下线更换真空槽。在顶枪发生堵塞后，需要停机维护顶枪喷头。双处理位的RH精炼装置共用一套真空抽气系统，依次切换到两个相邻的处理位进行真空处理。因此，一般而言，双处理位RH的两个工位的设备是等同的，但是如果配置不同的功能设备时，会对相关设备产生不同的影响。RH真空槽属于可维修部件，由于各部位耐材的工作环境不同导致对应的寿命和维护方式不同，其中RH真空槽的浸渍管在真空处理中插入高温钢水，处理结束后处于室温空气环境，而真空槽的下部槽在真空处理时会有高温钢水进入，处理完成后需要顶枪烘烤加热保温备用[2]。RH真空精炼装置的部分核心设备如图1所示。

图1 RH真空精炼装置

炼钢冶金生产作为典型的流程工业，其生产工艺非常复杂，所记录的生产运行数据虽然海量，但一般不直接反映设备的运行状况，需要设计针对性的方法获取可靠性数据。本文设计了依据生产记录数据进行可靠性分析的方法，并讨论RH顶枪对真空精炼装置的核心功能部件真空槽的影响。由连续时间序列分离出生产待机事件、故障事件和无故障事件，统计无故障间隔时间，形成分析样本，按照可靠性评估流程对RH真空精炼装置的核心功能部件真空槽设备运行可靠性进行分析和评估，计算各项可靠性评价指标[3-4]，从可靠性分析角度分析不同结构的RH顶枪对真空槽的影响。

经典的MTBF的观测值即为TBF，按下式计算：

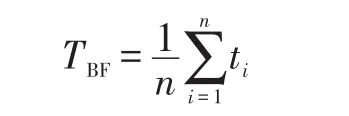
式中：ti为故障间隔的时间。

考虑到RH生产过程存在生产待机事件，并且在工艺待机过程中，设备处于加热保温状态，因此MTBF应该加上工艺待机时间，应按如下公式计算：

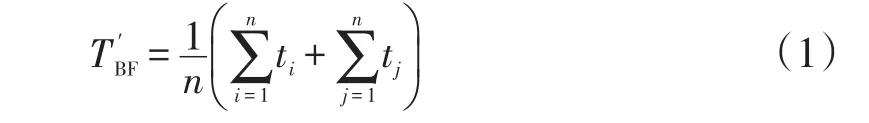
式中：tj为工艺待机时间。

而RH炉MTTR的观测值记为TCR，则按下式计算：

式中：tk为完成维修所需的时间。

固有可用度用来衡量设备正常工作的时间占比，即衡量设备的充分利用程度。其观测值可按下式计算：

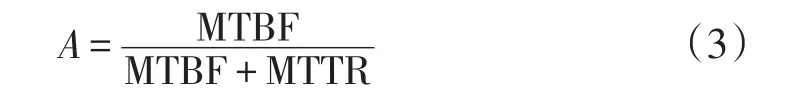
1 源数据处理

某钢厂180 tRH为双处理位RH真空精炼装置，顶枪作为主要功能部件用于对钢水加铝吹氧升温和对真空槽烘烤保温以及熔化消除真空槽内的冷钢。从2017年3月23日开始，在1#工位配置了环孔超音速集束射流的SCAP顶枪，在2#工位配置了圆孔超音速射流的KTB顶枪，两工位均按照原有KTB顶枪的运行参数进行真空精炼生产。在操作稳定后，选取部分连续时间的生产记录数据作为源数据进行分析，对比两工位真空槽运行的可靠性指标。

冶金生产的源数据包含了海量的信息，为了便于进行可靠性分析，选取从2017年4月1日至2017年5月31日共计61天的连续时间内的生产记录作为采样区间，每一炉次的生产记录作为一项样本事件。在此期间双处理位RH装置共处理了1 334炉次钢液，其中1#工位处理了672炉次，2#工位处理了662炉次，共计1 334件样本数据。在此连续时间序列的样本里包含了生产待机事件、故障事件和无故障事件，在进行可靠性分析时，需首先将这三种事件分离出来。在海量的生产数据中，提取日期、工位号、工序时间和钢水实际出站时间作为定义判别事件的有效数据。

双处理位RH装置正常的真空冶炼是连续、交替使用两个工位。生产待机事件由连续冶炼的间隔时间来判定，即当两工位同时出现冶炼时间间隔＞工艺设定时间阀值，则该事件为生产待机事件，该时间间隔计入生产待机时间。本分析设定的工艺时间阀值为120 min。

故障事件根据冶炼的工位号来判定，严格的工艺流程是双工位交替处理，但操作工在工序时间足够时，也会连续在同一工位上处理，但一般不超过4炉次。本案例假设发生连续4次及4次以上使用同一工位进行冶炼时，则说明另外一个工位发生了故障，计入另一工位的故障时间。

无故障事件是剔除生产待机和故障待机后的生产作业事件，其间隔时间计入无故障间隔时间。

在考核期内，1#工位和2#工位分离出的时间序列如表1所示。

根据统计数据，1#工位比2#工位多冶炼10炉次，剔除生产待机时间后的故障间隔时间，1#工位比2#工位多735 min；由此可见，在相同的时间轴上，故障间隔时间越长，用于生产冶炼的时间越多，因此，1#工位的SCAP氧枪比2#工位的KTB氧枪对真空槽的影响更小，SACP氧枪效能好于KTB氧枪。 故障间隔时间和故障修复时间统计数据见表2。

表1 1#工位和2#工位分离的时间序列

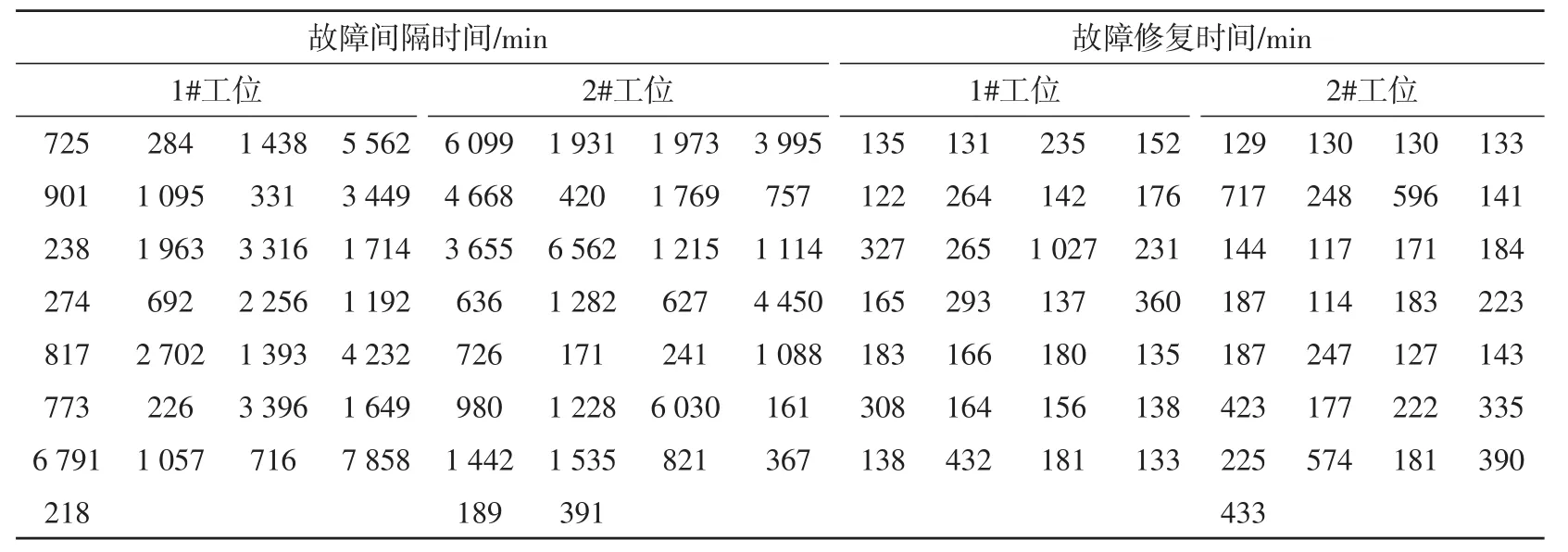
表2 1#工位和2#工位故障间隔时间观测样本

2 真空槽运行的可靠性函数模型

文献[5-6]基于故障数据对设备运行可靠性进行了分析与评估，本文依据该分析方法，从根据记录的连续时间序列，分离出1#工位、2#工位的无故障间隔时间，形成分析样本，分别建立起故障间隔时间概率分布模型。

2.1 故障间隔时间概率密度分布函数

根据分离出的故障间隔时间数据，制作累积频率计算表和累积频率分布图，拟合出故障间隔时间的概率密度函数。

数据分组遵循经验公式确定分组数k，即

式中：n为故障总次数。

确定分组数为6组，1#工位和2#工位取相同的组距1 283 min。统计落入各组的频数Δri和频率ωi，如表3所示。

由表2得到样本均值：1#工位的样本均值为2 041.3 min；2#工位的样本均值为1 914.4 min。

将各组频率除以组距Δt，取ωi/Δt为纵坐标，故障间隔时间为横坐标，故障频率分布图如图2所示。

由图2可知，在使用初期，RH炉故障发生率较高，且1#工位故障发生频率低于2#工位；在使用的中后期，RH炉的故障发生率降低。

故障间隔时间的故障频率直方图呈近似单调下降趋势，与常见的分布类型（指数分布、对数正态分布、威布尔分布）的概率密度曲线比较，该数据可能服从的分布为威布尔分布或指数分布。

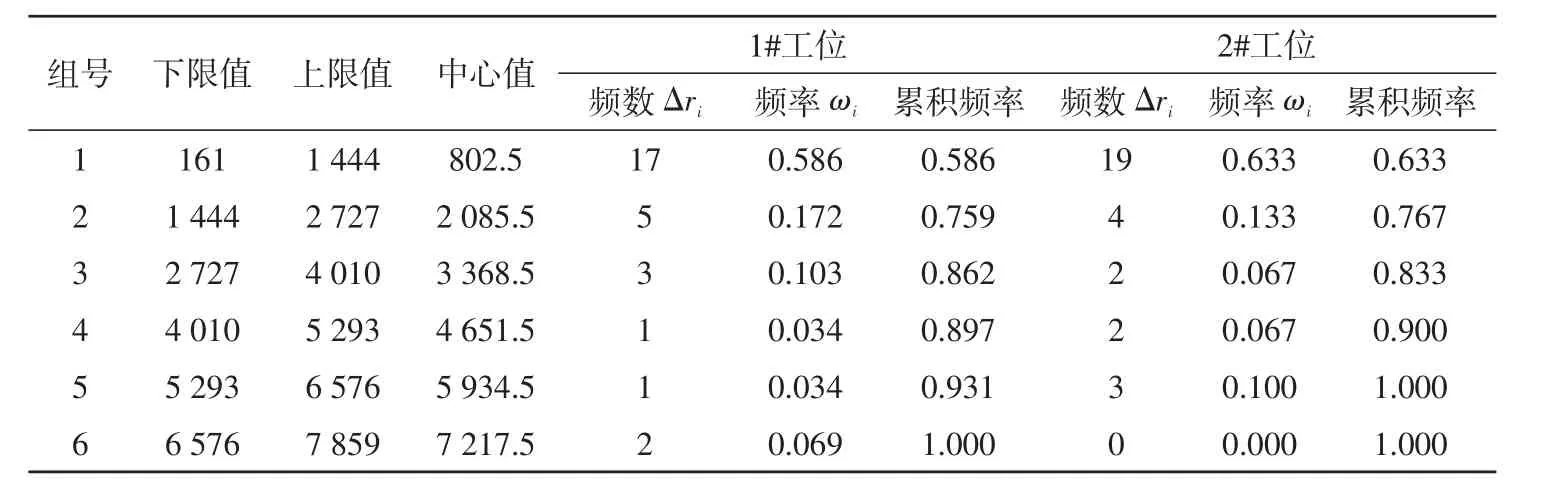
表3 1#工位和2#工位故障频率计算表

式中：ri为至i组结束时的累积频数，

以累积频率为纵坐标，故障间隔时间为横坐标，做累积频率分布图，如图3所示。

由图3可知，故障间隔时间的故障频率直方图呈近似单调下降趋势，累积故障频率直方图为单调上升，但斜率呈不断减小趋势，因此，该故障间隔时间可能服从指数分布或威布尔分布。初选分布模型后，需要对所选择的分布模型进行参数估计和假设检验。

图2 故障频率直方图

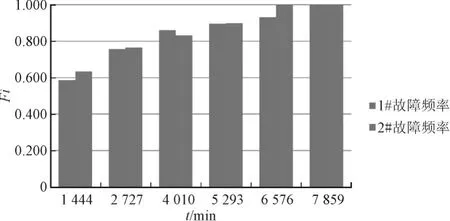
图3 累积故障频率直方图

2.2 故障间隔时间概率分布模型

初选分布模型故障间隔时间服从威布尔分布。双参数威布尔分布定义为

对双参数威布尔分布进行线性变换：

采用最小二乘法得到参数A、B的估计量和α、β：

通过最小乘法进行参数估计，首先对故障数据进行整理，小到大的顺序将实验过程得到的故障间隔时间ti进行排序，如表4所示。

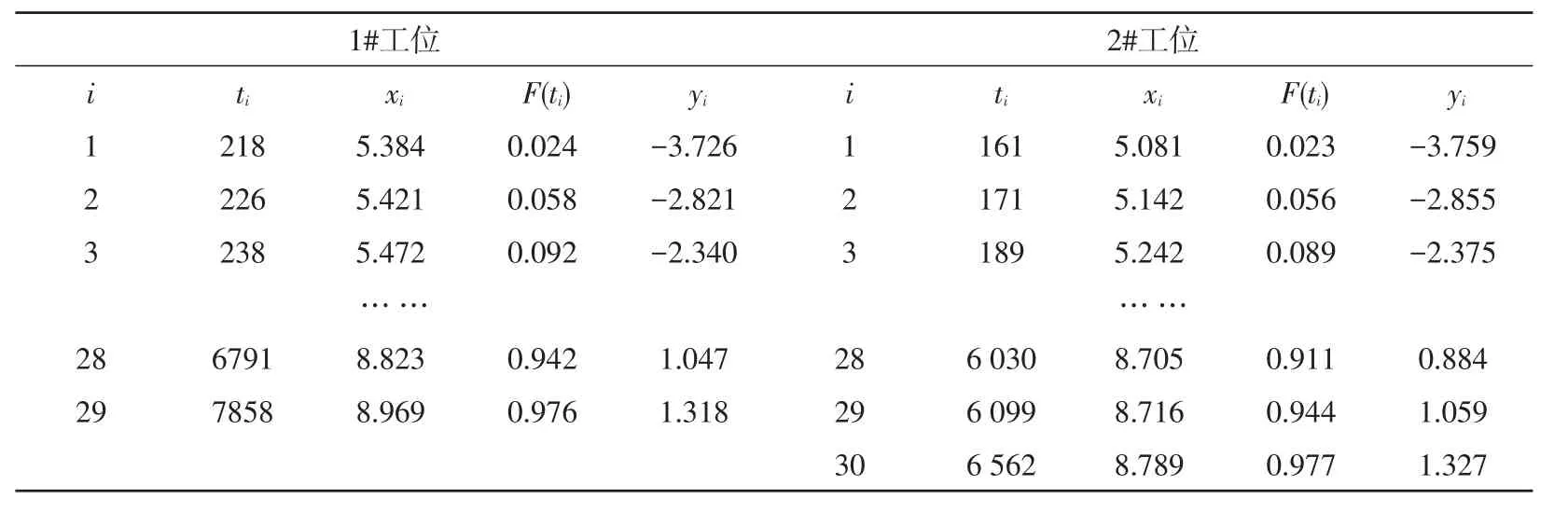
表4 1#工位和2#的故障数据

根据上述表格的数据和公式，可以计算估计参数，如表5所示。

表5 1#工位和2#估计参数

根据上述假设，得出RH炉累计故障分布函数，如表6所示。

表6 1#工位和2#故障分布函数

下面对威布尔分布进行假设性检验[7]。

通过试验得到的故障间隔时间按照从小到大的顺序进行排列，根据计算公式计算每个故障间隔时间对应的F0（ti），求出F0（ti）与经验分布函数Fn（ti）的差值。在得到的n个差值中，取绝对值最大的作为检验统计量Dn的观测值。然后将Dn与临界值Dn,a进行比较，若满足公式，即可认为模型是正确的。

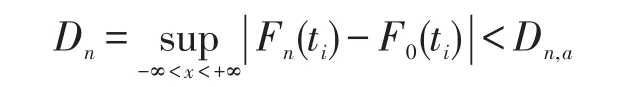
式中：F0(ti)为原假设分布函数

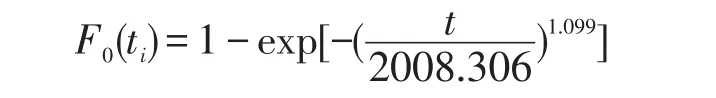
式中：Dn,a为临界值，取显著性水平α=0.1，通过查表可得Dn,a=

由公式和统计数据可知，该模型服从两参数威布尔分布，如表7所示。

3 可靠性评价指标

前面得到了故障间隔服从的分布模型，下面进一步评定常用的可靠性特征量：MTBF、MTTR、和固有可用度A。将以上数据带入式（1）～式（3），可以获得RH真空槽设备的运行可靠性指标，如表8所示。

表7 1#工位和2#假设性检验

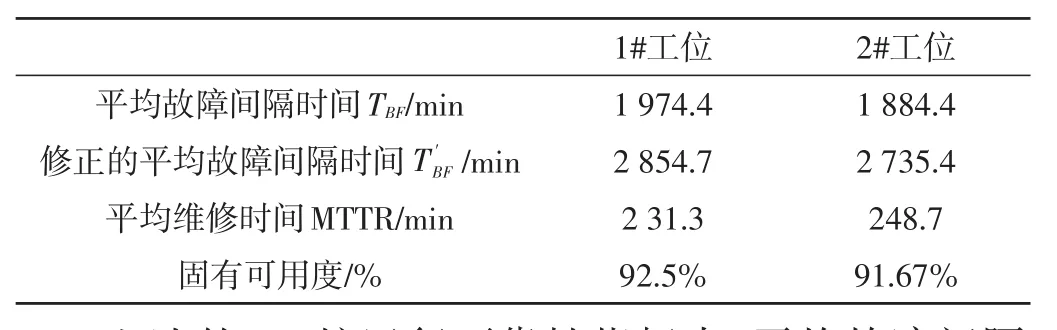
表8 1#工位和2#可靠性评价指标

上述的RH炉运行可靠性指标中，平均故障间隔时间MTBF越大，表明可靠性越高，RH炉正常工作能力越强；平均故障维修时间MTTR越小，表明RH炉恢复性越好；固有可用度A越大，表明RH炉有更多的时间用于正常生产。由各项可靠性指标可知，1#工位运行情况好于2#工位。

设备运行可靠度是设备在规定条件下和规定时间内完成规定功能的概率，即可靠性的概率度量。

前面已经确定该设备的故障间隔时间分布函数服从威布尔分布，根据上述的双参数威布尔模型，可得故障密度函数f（t）、故障分布函数F（t）、故障率函数λ(t)，可靠度函数R（t）四类函数模型，如表9所示。

表9 1#工位和2#四类函数模型

1#工位和2#工位的四类可靠性函数曲线如图4所示。

图4 四类可靠性函数曲线

由图4可知，在相同的生产环境下SCAP顶枪和KTB顶枪对RH真空槽设备的运行可靠性影响相当，SCAP顶枪好于KTB顶枪。

4 结论

炼钢冶金生产作为典型的流程工业其生产工艺非常复杂，实时记录的生产运行数据虽然海量，但一般不直接反映设备的运行状况，需要设计针对性的方法获取可靠性数据。本文从海量的生产运行数据中提取有效信息，并结合实际的生产工艺流程进行数据处理，可以完成冶金设备的运行可靠性分析。

利用可靠性分析方法，可以判定功能部件对核心设备运行的影响。对从生产现场采集的数据进行可靠性分析表明：在相同的生产环境下SCAP顶枪和KTB顶枪对RH真空槽设备的运行可靠性影响相当，SCAP顶枪好于KTB顶枪。