桥梁微形变微波干涉测量算法研究

潘 越， 马 宁， 吴向上， 孟庆良

(1.上海无线电设备研究所，上海201109;2.上海机电工程研究所，上海201109)

0 引言

随着桥梁行业的飞速发展，微形变监测技术对桥梁的健康普查和灾害预防具有重要意义。与传统微形变监测方法相比，微波干涉测量法具有高精度，非接触式远距离测量和实时测量等无可比拟的优势。微形变检测是对变形体进行测量以确定其空间位置及内部形态的变化特征，目前微形变检测已经有很多相对成熟的测量方法，包括常规大地测量方法、专门测量法、摄影法等[1]。常规大地测量法并不是一种新兴的测量技术，无论是测量仪器还是理论都经过了时间的考验，所以测量结果也相对安全可靠[2]。这种测量方法观测费用低、适用性广、精度高，能够适用于不同工作环境和检测物。但是同时也有一定的局限性，测量过程耗时久，需要大量的劳动力，导致测量效率低下，而且遇到雨雪等恶劣天气还会影响测量结果的准确性[3]。专门的测量方法(例如加速度传感器)的优点是相对精度高，而且专用仪器种类丰富、选择空间大，其缺点是测量范围小，安装费时费力。摄影测量的方法可以利用少量的观测点数来获取观测目标的局部或者完整的样貌[4]。摄影测量法的优点是可以完整地获取观测目标的变形信息，具有快速直观全面的特点，可以减少户外工作量，还可以远距离测量[5]。它的缺点是测量精度低，对光线要求高，需要拍摄大量照片，不适于定点测量[6]。常规的检测方法虽然理论成熟，但大都存在一定的局限性，不能进行大范围短时间地测量，效率不高需要劳动量大，且检测设备无法在恶劣天气下正常工作等。本文所研究的微波干涉测量法，能够对远处的目标点进行非接触式测量，测量周期短，测量精度高且不易受天气、温度和环境的影响。此外，还具有便携、安装简单等优点，因此在微形变测量领域具有广泛的应用前景。

1 理论基础

1.1 干涉测量技术

干涉测量技术是通过对比雷达不同时刻的两次回波信号的相位差来获取目标的微形变信息，其原理如图1所示。利用干涉测量技术，即使目标产生毫米级别微小的变形也能被发现并测量出来。干涉测量法测量微形变的公式为[7]

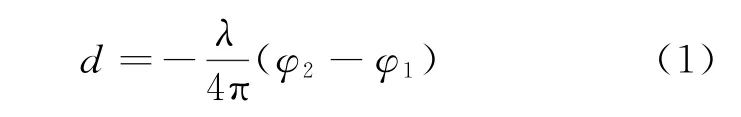
式中：λ 为发射电磁波波长;φ1为被测目标第一次回波信号的相位;φ2为被测目标第二次回波信号的相位;d 为雷达视线方向的微形变。

图1 干涉测量原理图

1.2 合成孔径雷达理论

合成孔径雷达(Synthetic Aperture Radar，SAR)是选用小尺寸的天线向空间辐射电磁波信号，雷达沿着轨道方向运动，在运动过程中不断地发射接收信号，并将接收到的信号按顺序存储起来[8]。真实孔径雷达是在同一位置接收目标的回波信号，合成孔径雷达则是在不同位置接收同一目标的回波信号。合成孔径雷达天线的尺寸不需要很大，很小的天线就可以通过相对运动产生一个等效的大孔径的线性阵列天线[9]。合成孔径雷达接受到的信号不是同时采集的，所以需要将天线在各个位置发射的信号和接收到的目标回波按顺序储存，并对一定时间间隔内的接收信号进行处理，完成雷达成像[10]。合成孔径长度Ls是目标仍在天线波瓣宽度之内雷达运动的最大距离，合成孔径雷达的最大合成孔径长度Ls可以表示为

式中：λ 为天线辐射电磁波的波长;D 为天线的真实孔径;R 为雷达与目标之间的斜距。

1.3 后向投影算法

后向投影(Back Projection，BP)算法是一种典型的SAR 时域成像算法。延迟-求和为后向投影算法的核心思想，通过对回波信号延迟时间的计算实现回波信号的相干叠加，将接收到的回波信号反向投影到所需测量区域的每个像素点位置处，累加不同角度的像素值，进而获取对应点的散射强度信息完成目标高分辨成像[11]。

BP算法需要对成像区域中的各像素点执行逐一匹配操作，算法第一步需要对成像区域进行网格划分，对成像空间进行离散化操作得到M 个像素点;算法第二步对信号从发射天线到各像素点以及从各像素点返回至接收天线的时间和进行计算，根据相关往返耗时获取对应位置的幅值信息，将轨道上各位置所有回波信号的幅值进行累加得到对应点幅值完成成像。BP 算法成像的工作流程图如图2所示。

后向投影法成像公式的离散形式为

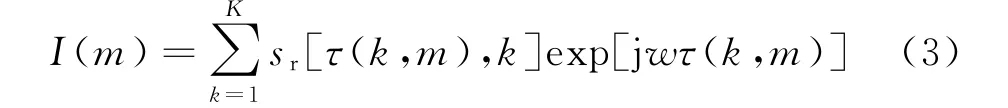
式中：I(m)为第m 个像素点的散射系数，m=1，2，…，M;Sr[τ(k，m)，k]为第m 个像素点在第k 个位置处回波信号的幅度值;τ(k，m)为第m 个像素点到第k 个位置的双程时延。

2 模型搭建

2.1 测量模型

桥梁的微形变测量主要是测量桥面垂直于地面方向上产生的微小位移，实际工程中很难直接测得，而是通过测量雷达与目标连线方向上的位移变化量计算出桥面垂直方向上位移。测量模型如图3所示，雷达与地面之间的夹角是α，目标与

图2 BP算法流程图

雷达的相对距离为R，雷达与目标连线方向上产生的变化量是ΔR，进而计算出桥面垂直方向产生的位移为

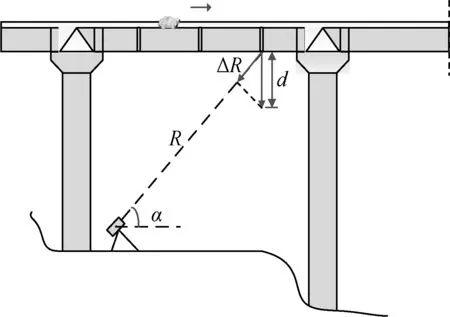
图3 微波干涉测量法测量模型

2.2 信号模型

步进频率信号是一系列窄带脉冲组成的合成宽带信号，能够获得高分辨率，在降低雷达体积、重量和成本方面具有显著作用[12]。步进频率信号的实质是线性调频信号的离散化形式，是以一定步长连续变化的N 个正弦(或余弦)信号序列，主要分为脉冲和连续波两种信号形式。脉冲信号是在每个频率上发射一个窄带脉冲信号，脉冲信号体制下信号源的结构相对复杂，但其脉冲本身具有解算距离的能力，能够求解距离模糊，所以可以测量更远的距离。连续波信号是在频率变化之间信号持续发射，信号能量大，能够降低对发射机峰值功率的要求，但不能计算距离模糊，作用距离相对较近[13]。步进频率连续波的示意图如图4所示。

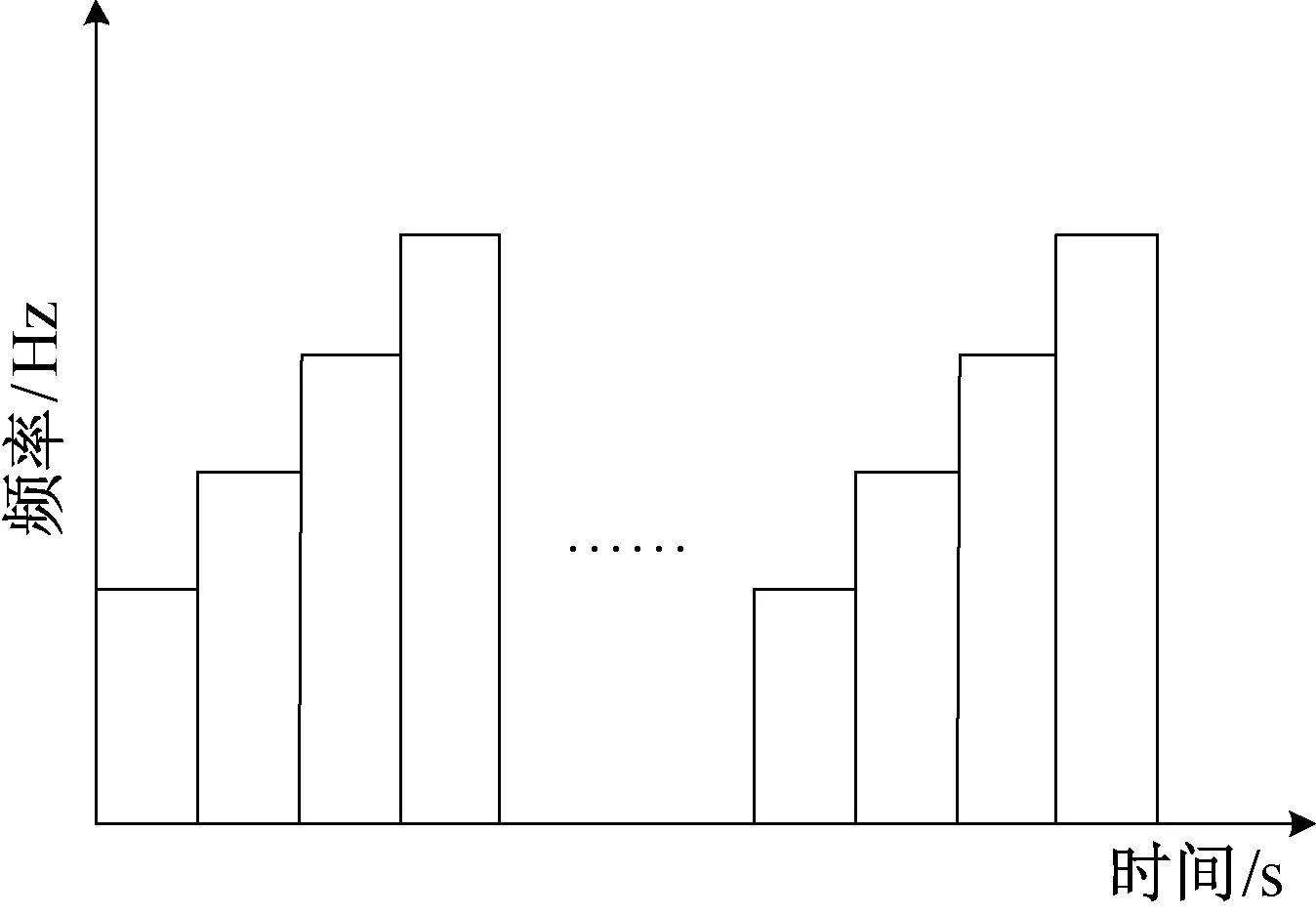
图4 步进频率连续波示意图

步进频率信号的一般形式为

式中：Tr为脉冲重复周期;τ 为发射脉冲宽度;Δf为步进频率量;N 为频率步进数。

雷达在长度为L 的轨道上匀速运动，并按一定时间间隔向目标区域发射N 个脉冲的步进频率连续波，由于信号持续时间很短，假设雷达在发射和接收信号期间是静止的，即雷达与目标之间未发生相对运动。雷达每移动长度Δl 的距离发射和接收一次信号，雷达在导轨上走完单程发射和接收M 帧信号完成一次数据的采集，然后雷达重新返回起点重复上述运动，完成多次数据的收集和存储经过信号处理后按照一定的成像算法分别成像。发射的步进频率连续波波形图如图5所示。

3 微波干涉测量法

基于步进频率连续波的微波干涉测量法具有高精度，非接触式测量和实时测量的优势。雷达在固定的水平轨道上匀速运动，通过持续向外辐射电磁波信号获取目标点的位置信息。距离向利用电磁波从雷达到目标的用时来计算二者的相对距离。方位向是利用合成孔径获取目标高分辨率的方位向信息。确定距离信息与方位信息后，对已知目标点进行微形变的测量，利用干涉测量原理计算多次测量的回波信号的相位差来获取目标点的微形变。

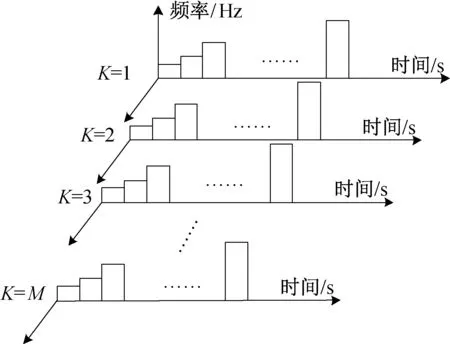
图5 发射信号模型

图6 后向投影法

3.1 目标定位

对目标点微形变的测量首先要对目标的定位，本文选用BP 算法对目标进行成像确定目标的位置信息。首先对成像目标区域进行离散化处理，将它分成P×Q 个均匀的像素点，P、Q 分别代表雷达视线方向和沿轨道运动方向像素点的个数。设合成孔径雷达的角度分辨率为Δθ，距离分辨率为Δr，轨道长度为L，在轨道上一共有m 个位置进行数据的采集。雷达在每个位置上都进行一次信号的发射和接收，采集到的数据可以看作是时间阵列，每个阵元的位置记为m，其中目标区域中任意像素点(p，q)与第m 个位置之间的相对距离记作Rm。步进频率连续波以固定的重复周期沿方位向发射接收信号，在第m 个位置发射的信号形式为

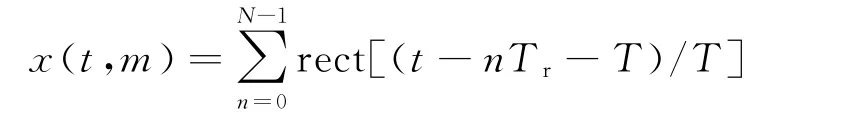
从上述成像过程可以看出先对回波信号进行傅立叶逆变换完成距离向聚焦，然后再利用合成孔径后向投影算法完成方位向聚焦，最终完成目标点的二维成像。

3.2 微形变测量

完成对目标点的成像后，我们可以通过二维图像上确定测量点的位置，然后利用干涉测量法同时对多点进行微形变检测，目标点的微形变测量过程如图7所示。设两次接收到的回波信号表示为

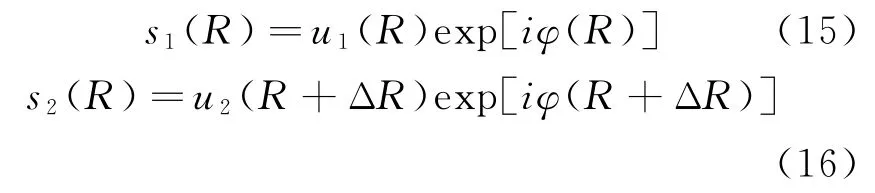
接收信号的相位信息由往返路径确定，可得

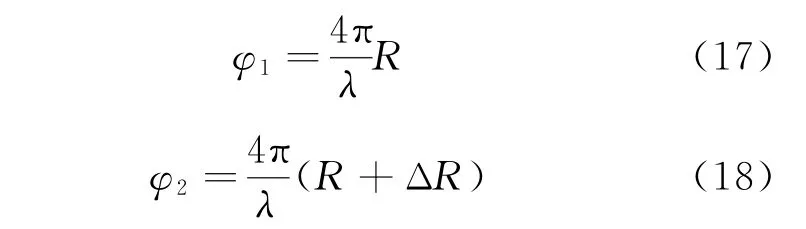
第一次回波信号与第二次回波信号的共轭相乘

提取干涉相位，得

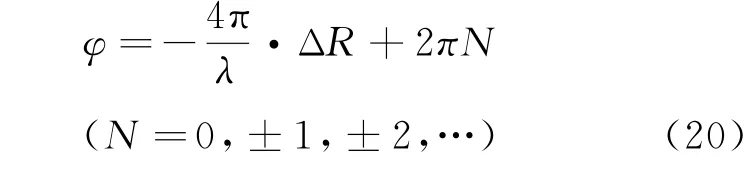
从而得到微形变量为

最后利用公式(4)计算出桥面垂直方向的微小位移d。

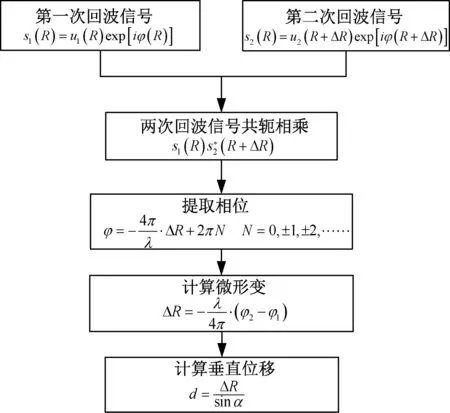
图7 二维点目标微形变测量过程

4 仿真分析

发射一串含有256个单频脉冲的步进频率连续波信号，每个脉冲信号持续时间为1μs，起始频率为17.1 GHz，其单频脉冲间的步进频率为1 MHz。设雷达在长度为2 m 的轨道上作匀速直线运动，每隔0.005 m 完成一次信号的发射和接收，2 min走完一次全程。下面在信噪比为20 dB，三个目标点的位置坐标分别为(100，4)，(100，10)，(100，16)的条件下，对多目标点的二维成像进行仿真。得到目标点成像的仿真结果如图8所示。

图8 目标点的成像结果

由仿真图8可知，在停-走-停假设条件下，合成孔径雷达在固定导轨上匀速运动，以固定频率发射和接收步进频率连续波，完成数据的采集，然后对二维回波信号进行信号处理，进而能够很好地完成合成孔径雷达二维成像，能够很好达到对目标点定位的目的。

4.1 微形变测量仿真分析

在目标位置和雷达仰角确定的前提下，可以利用干涉测量对目标点进行长时间实时测量。假设雷达的一次测量周期为3 min，目标点在距离向每隔3 min发生0.2 mm 的微形变，下面对目标点60 min内形变量的测量进行仿真。将测量的微形变值与理论微形变值进行比较，得到的测量误差如图9所示。

仿真图9反映的是目标点微形变测量值与实际微形变值的差值，从图中可知绝大部分点的测量误差范围在(-0.1 mm，0.1 mm)，证明了干涉测量的准确性和高精度，精度能够达到0.1毫米级。

4.2 信噪比对测量精度的影响

图9 二维干涉测量微形变测量误差

通过对微波干涉测量算法的仿真，已经证实了设计的基于步进频率连续波的微波干涉测量法能够有效准确地测量出多目标点的微形变，在20 d B信噪比的情况下，测量精度能够达到0.1毫米级。下面就针对信噪比对多目标点微形变测量精度的影响进行讨论。仿真参数设置与表1相同，分别在信噪比为5，10，15，20，25，30，35，40，45，50 d B，的情况下，对每一个点目标重复300次微形变的测量，然后求出其均方根误差。图10给出了不同信噪比情况下，三个目标点微形变测量值的均方根误差。

图10 信噪比对点目标测量精度的影响

由仿真结果可知，随着信噪比的增大，不同目标点微形变测量的误差逐渐减小，且不同点处的测量精度不同;当信噪比大于30 dB时，三个目标点的测量误差相差不大;综上所述，信噪比虽然在一定范围内能够影响微形变检测算法的测量精度，且对不同位置处目标点测量精度的影响各不相同，但只要在信噪比大于15 dB 的环境下仍然能够保证对多目标点微形变测量的精度在亚毫米级，证明了该算法具有很高的测量精度，能够有效测量目标的微形变。

5 结论

本文分析了微形变检测在桥梁微形变监测领域的优势和应用价值，利用微波干涉测量法对目标微形变进行高精度和远距离的测量，并通过Matlab仿真验证了算法的可行性与准确性。首先利用后向投影算法对目标点进行定位，然后利用干涉测量技术计算出微小位移，最后通过比较分析不同信噪比对测量精度的影响，当信噪比大于15 dB时该算法测量精度能达到0.1 mm，说明本文提出的基于步进频率连续波的微波干涉测量法能够有效的测量计算出目标点微小位移。