Survey on angle-based classification*

FU Sheng, XUE Yuan, ZHANG Sanguo

(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)(Received 2 January 2018： Revised 24 April 2018)

Abstract Statistical classification problems are widely encountered in many applications, e.g., face recognition, fraud detection, and hand-written character recognition. In this article we make a comprehensive analysis on statistical methods for supervised classification problems. Specifically, we introduce the angle-based classification structure, which combines binary and multicategory problems in a unified framework. Several new variants of the angle-based classifiers are also discussed, such as robust learning and weighted learning. Furthermore, we show some theoretical results about Fisher consistency for these angle-based classifiers.

Keywords angle-based classification framework; Fisher consistency; robust learning; statistical classification; weighted learning

Classification is an important type of supervised learning problems for information extraction, which has attracted widespread attention among the machine learning and statistics communities. For example, assigning a given email into “spam” or “non-spam” class and optical character recognition task are two typical examples of statistical classification problems[1-2].

1 Statistical classification

For a supervised classification problem withkclasses, the training set consists ofnsamples {(xi,yi),i=1,…,n}, which are independently and identically drawn from an unknown probability distributionP(X,Y). Here, the inputxidenotes ap-dimensional covariates vector, andyi∈Ck≜{1,…,k} is the corresponding class label.

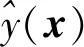
There are many different kinds of classifiers, which follow different criteria. Naive Bayes method follows the maximum a posterior decision rule. Fisher linear discriminant analysis is designed under some fundamental assumptions, i.e., the normally distributed classes. Based on the concept of entropy from information theory, decision tree learning is devised for classification. Neighbour-based learning is another type of classification based on instances, and it takes the local instances’ similarity into consideration. Artificial neural networks are inspired by the biological neural networks. For more details, one can see Refs.[3-5]. In this article, we focus on the margin-based classifiers, which have drawn a great attention in the statistical machine learning community.

The rest of this article is organized as follows. In section 2, we briefly review some existing traditional classification methods, including binary and multicategory problems. We present a novel angle-based framework in section 3, which is more computationally efficient. We also show some new developments to handle multicategory problems under some complicated settings. In section 4, several theoretical results about Fisher consistency are summarized. Some discussions and suggestions are given in section 5.

2 Traditional methods

We first give a brief review on regularization framework for binary classification in section 2.1, the extension for multicategory cases is then presented in section 2.2.

2.1 Binary classification

(1)

where F is the functional space of interest,J(f) is the roughness penalty offto measure its complexity and consequently prevent the resulting classifier from overfitting, andλ≥0 is a tuning parameter that controls the balance between the goodness of fit and the penalty term.

The commonly used binary convex loss functions are listed as follows.

·hinge loss[7-8]:l(u)=[1-u]+≜max(0,1-u).

·perceptron loss[9]:l(u)=[-u]+.

·logistic loss[10-11]:l(u)=log(1+exp(-u)).

·exponential loss[12]:l(u)=exp(-u).

·least square loss[13]:l(u)=(1-u)2.

·squared hinge loss[14]:l(u)=([1-u]+)2.

·LUM loss (large-margin unified machine[15]): for givena>0 andc≥0,

·DWD loss[15-17]: it can be viewed as LUM loss witha=1 andc=1, i.e.,

(2)

Except for perceptron loss, the above-ment-ioned loss functions can be viewed as the surrogate convex envelope of 0-1 loss, which helps to make the loss term be convex and computationally tractable.

For simplicity, we only consider linear form offto show the penalty term. Assume thatf(x)=ωTx+b, whereω=(ω1,…,ωp)T∈Rpis the coefficient vector for the predictors, andb∈R is a scalar as the intercept. We are interested in parametersωandb, which are the solution of problem (1). There are various choices for the penalty termJ(f), and we show several forms for penalty function as follows.

·L2penalty[7-8]:

·L1penalty[18]:

·Lqpenalty[19]:forq≥0,

·Elastic-net penalty[20]: forα∈[0,1],

There are still many well-known penalties in the literatures such as group LASSO[21], SCAD[22], and MCP[23], which can be used for classification tasks.

The loss term and penalty term have various choices, and their combinations connect several meaningful classifiers. By properly choosing loss function and penalty term, problem (1) can be solved efficiently via the standard convex optimization[24].

2.2 Multicategory classification

The aforementioned methods are originally designed for binary problems. In practice, it is prevalent to have more than two classes in the dataset. However, generalizations to multicategory case are extremely challenging. To solve a multicategory problem, there exist two common approaches in the literature. One is to solve a sequence of binary problems and combine the results for multicategory classification, e.g., one-versus-rest and one-versus-one[25-26]. This approach is suboptimal in certain situations. One-versus-one method suffers a tie-in-vote problem, and one-versus-rest method is inconsistent when there is no dominating class[27-28]. The other approach is to consider allkclasses in one optimization problem simultaneously. One common method to handlek-class problems is to usekdecision functions, which representkdifferent labels. The corresponding prediction rule is based on which function is the maximum.

Letf=(f1,…,fk)Tbe a vector-valued decision function, which is a mapping from Rpto Rk. Note that an instance (x,y) is misclassified byfify≠arg maxj∈{1,…,k}fj(x). However, such a procedure has some drawbacks. For example, assume thatf*is the optimal decision function, but it may not be unique. If we add a constantcon all components off*, the newf*+cmay have the same classification prediction accuracy asf*. Thus, a sum-to-zero constraint is commonly imposed on thesekfunctions to reduce the parameter space as well as to ensure good theoretical properties. Similar to problem (1), the corresponding optimization problem for the multicategory classification can be typically written as

(3)

withV(·,·) being a loss function for a multi-category case, andJ(f) being a regularization term defined for the decision function. Naturally,J(f) can be designed separately for allkcomponents based on the definitions of penalty in section 2.1. Clearly, when a sum-to-zero constraint is employed for margin-based classifiers, formulation (3) withk=2 is equivalent to the binary classification problem in (1).

There are several different extensions of binary methods to the multicategory problems. Here, we list several commonly used loss functions as follows.

·Naive hinge loss:V(f,y)=[1-fy]+.

·V(f,y)=∑j≠y[1-(fy-fj)]+,see Ref.[29].

·V(f,y)=[1-minj≠y(fy-fj)]+,see Ref.[30].

·V(f,y)=∑j≠y[1+fj]+,see Ref.[27].

·V(f,y)=γ[k-1-fy]++(1-γ)∑j≠y[1+fj]+withγ∈[0,1], see Ref.[28].

·V(f,y)=γ(k-1-fy)2+(1-γ)∑j≠y(1+fj)2withγ∈[0,1], see Refs.[31-32].

·V(f,y)=γlLUM(fy)+(1-γ)∑j≠ylLUM(-fj) withγ∈[0,1], see Ref.[33].

We can abstract two kinds of functional margins for the multicategory classifiers. One is absolute margin, such as those in Refs.[27-28,31-33], which considersfjs separately in additive loss functions. The other is relative margin, e.g., those in Refs. [29-30], which considers the pairwise comparisons {fy-fj,j=1,…,k,j≠y}. They both encourage the componentfyto be larger than the other components under the explicit or implicit sum-to-zero constraint.

Many large margin classifiers may suffer serious drawbacks when the data are noisy, especially when there are outliers in the training data. In Refs. [34-37] the authors showed that the truncation of loss function helps to obtain robust classifiers, such as the truncated hinge loss, truncated exponential loss, and truncated logistic loss. Wu & Liu[38]applied the weighted learning techniques for robust classification performance and efficient computation.

3 Advanced classification methods

For multicategory classifiers withkdecision functions, under the sum-to-zero constraint, its degree of freedom should bek-1, naturally. It can be verified straightforwardly, e.g., only one function is needed for binary classification task. Thus, it should be sufficient to usek-1 functions fork-class problems. The inefficient sum-to-zero constraint makes the optimization problem (3) be more time-consuming and prohibitive. Recently, Zhang & Liu[39]proposed a novel angle-based classification framework without sum-to-zero constraint, which can enjoy better prediction accuracy and faster computational speed. Thus, the angle-based classifiers can be more competitive. We show the details about angle-based classification in section 3.1, and present several recent developments on the angle-based methods in section 3.2.

3.1 Angle-based classification

Angle-based classification considers ak-vertex simplex structure in an Euclidean space Rk-1, with one less thankcategories[40-43]. To be more specific, denoteWbe a collection of vectors {Wj,j=1,…,k} in Rk-1with

where1k-1is a vector of lengthk-1 with all entries 1, andej∈Rk-1is a vector of 0’s except itsjth entry is 1. Without loss of generality, assume thatWjrepresents the classj(j=1,…,k). One can verify that the setW={W1,…,Wk} forms a centered simplex withkvertices in Rk-1. The center ofWis at the origin, and allWjs have the same Euclidean norm 1.

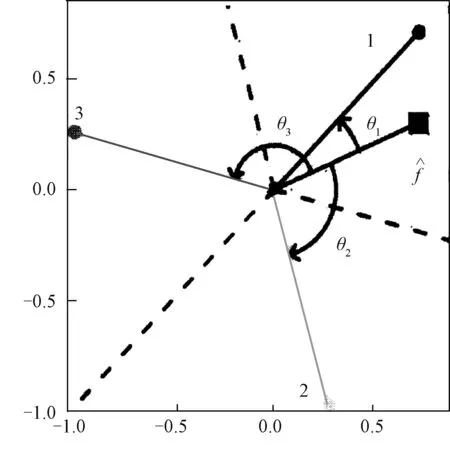
Fig.1 The classification regions and prediction rule when k=3 (from Ref.[39])

Motivated by Ref. [39], we propose a general optimization framework for the angle-based classifier as follows

(4)

whereφ(f(x),y) is a well-designed loss function for angle-based classification. For example, Ref. [39] used the margin-based lossφ=l(〈f(x),Wy〉), wherel(·) is an arbitrary binary large-margin loss function, the arguments ofφare suppressed in the expressions for simplicity.

In a flash I knew -- she had made it for her mother, a mother she would never see again, a mother who would never hold her or brush her hair or share a funny story, a mother who would never again hear her childish joys or sorrows

One can see that the sum-to-zero constraint can be avoided naturally. With less parameters than problem (3), the framework (4) may become more compact and concise.

3.2 New developments

Note that the loss functions for multicategory classifiers can be abstracted two types in section 2.2. Analogously, we can extend them to inner product functional margins for angle-based classi-fiers. One is absolute functional margin, which deals with thekinner products {〈f,Wj〉,j=1,…,k} separately and encourages larger 〈f,Wy〉 and smaller {〈f,Wj〉,j≠y} on the instance (x,y). We consider the following type I loss function

φ1=γl1(〈f(x),Wy〉)+

(5)

wherel1andl2are arbitrary binary margin-based loss functions. The reinforced angle-based multicategory SVM in Ref. [44] followed the loss function (5). Based on the numerical results of Refs. [28,44], the best choice ofγis 1/2 with stable classification performance.

The other is relative functional margin, which handles the difference quantities {〈f,Wy-Wj〉,j≠y}, and encourages larger positive gap for correct classification. We design the type II loss as follows,

(6)

The variety of loss functions (5) and (6) contributes to enrich the family of angle-based classifiers. In particular, whenγ=1 in (5), it reduces the original angle-based classifier[39], and they employed the LUM loss for classification under

angle-based structure.

(7)

and the weighted type II classifier,

Wyi-Wj〉)+λJ(f),

(8)

whereωi,jin (7) andωiin (8) are nonnegative weights for all observations. Reference [45] also show serval strategies for choices of weights.

Denote the truncated loss function ofl1(·) andl2(·) beTs(u)=min(l1(u),l1(s)) andRv(u)=min(l2(u),l2(v)), wheresandvare the corresponding truncation location parameters. Inspired by the truncated loss and robust learning in Refs. [34-37], we devise the truncatedφ1andφ2to achieve robust angle-based classification as follows,

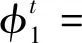
(9)

and

(10)

For example, Ref. [46] studied the robust angle-based SVMs based on the truncated hinge loss functions, which followed the formulations of truncated loss (9) and (10).

The weighted learning problems for (7) and (8) can be solved by efficient convex optimization techniques, while the robust learning based on the non-convex truncated loss (9) and (10) are more complicated and challenging, which can be solved via difference of convex algorithms[45-46]. They both can enjoy stable performance against potential outliers. Interestingly, the adaptively weighted angle-based classifiers have a close connection with the classifiers based on the truncated loss. Reference [45] showed that the algorithms of weighted learning and truncated learning are equivalent to each other in terms of fixed point.

Recently, we proposed a new family of loss functionVρ(·) as follows,

(11)

whereρ>0 is a scale parameter. AlthoughVρ(·) is non-convex and without any truncation, its boundedness property contributes to robust performance. Thus, in order to estimate robust individual treatment rules, we employedVρ(·) under the angle-based framework (4), and proposed robust outcome weighted learning (ROWL). The proposed ROWL method can enjoy Fisher consistency, and provide estimation for the ratios of two different outcomes. Furthermore, it can yield more competitive performance than some existing methods注This part is from Fu’s recent paper “robust outcome weighted learning for optimal individualized treatment rules”..

For the disease forecasting problems, there may exist one special variable in the feature space, which needs to be singled out to preserve its effects from other variables, e.g., the age-dependent effect in bioscience. A novel method, targeted local angle-based multicategory SVM (TLAMSVM) was proposed to construct effective age-dependent classification rules. The TLAMSVM method followed the weighted angle-based classification (7). The age-specific prediction rule is very useful to guide personalized treatments注This part is from Zhang’s recent paper “targeted local angle-based multi-category support vector machine”..

4 Theoretical results

In this section, we focus on Fisher consistency, which is a fundamental property of a classifier[47-52]. For multicategory problems withk≥2, the issue of Fisher consistency becomes more complicated. Set the class labels be {1,…,k}. For an observationx, denote the conditional probability bePj(x)=Pr(Y=j|X=x). Fisher consistency for an angle-based classifier is defined as follows.

Definition4.1(Fisher consistency[39,44-46]). LetV(·,·) be a general margin-based loss function. Supposef*be the theoretical minimizer of the conditional loss E[V(f(X),Y)|X=x] for any observationx. If

holds, we say that the loss functionVand the corres-ponding angle-based classifier is Fisher consistent.

In other words, Fisher consistency means that if we are using infinitely many training instances and an appropriate functional space F, then the learned angle-based classifier can achieve the best classification accuracy theoretically.

Next, we show some results about Fisher consistency for angle-based classifiers in the following theorems.

Theorem4.1(Refs. [39,53-54]). Consider the angle-based classification framework (4),

A1.Assume a general margin-based lossφ=l(〈f(x),Wy〉). Ifl′(u)<0 for allu, it is Fisher consistent.

A3.For the DWD lossφ=lDWD(〈f(x),Wy〉) in (2), it is Fisher consistent.

A4.For the new lossφ=Vρ(〈f(x),Wy〉) in (11), it is Fisher consistent forρ>0.

Remark4.1A3 and A4 both satisfy the condition of A1, which can be viewed as a special examples of A1.

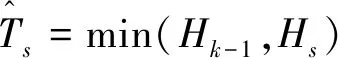
Theorem4.2(Refs. [44-46]). Consider the type I angle-based loss function (5) and its truncated version (9),

B1.Suppose the reinforced hinge loss beφ1=γHk-1(〈f(x),Wy〉)+(1-γ)∑j≠yH1(-〈f(x),Wj〉) withγ∈[0,1], it is Fisher consistent forγ∈[0,1/2].

B3.For the reinforced least square lossφ1=γ(k-1-〈f(x),Wy〉)2+(1-γ)∑j≠y(1+〈f(x),Wj〉)2withγ∈[0,1], it is Fisher consistent for all values ofγ∈[0,1].

B4.Ifli′(u)<0 (i=1,2) for allu, then the general loss (5) is Fisher consistent for all values ofγ∈[0,1].

Remark4.2Due to the differences between the employed loss functions, case B1-B5 have different consistent intervals forγ. Concretely speaking, the hinge loss in B1 and its truncated version in B2 are non-differentiable at the hinge point and truncation point, thus they may lead to narrower consistent intervals than B3-B5.

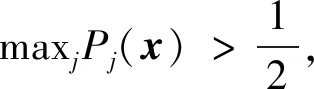
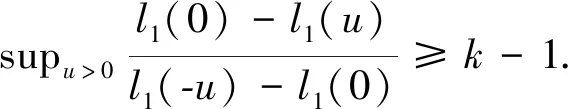
Remark4.3For the general loss functionl1in (6), C1 and C2 impose two different conditions to achieve Fisher consistency. C1 emphasizes on the conditional class probability, i.e., the existence of dominating class. While C2 restricts the mathematical property of loss function. C3 also fulfills the condition of C4, which can be regarded as a special case of C4.

We summarize the results of Theorem 4.1, 4.2 and 4.3 in Table 1 for a comprehensive view.

Table 1 Summary of Fisher consistency results for several angle-based classifiers

5 Discussion

In this article we give a brief survey on the statistical classification methods under the regularization framework including binary and multicategory problems, ranging from traditional and advanced methods. The novel angle-based framework connects binary and multicategory problems in a single structure, and can be optimized efficiently without the redundant sum-to-zero constraint. We discuss some new extensions of angle-based classifiers such as robust learning and weighted learning.The theoretical results about Fisher consistency are also presented. We believe that the new angle-based classification and its extensions are very promising research topics.

The angle-based framework opens a door to advanced statistical classification methods, and it will be very interesting and meaningful to generalize this procedure to certain situations. We briefly discuss several suggestions for the future research. Firstly, in a high-dimensional low-sample-size (HDLSS) setting, the multicategory classification problems become more challenging, and the authors of Ref. [54] give a pioneering work as an extension of general DWD to handle multiclass HDLSS case. Secondly, the choice of loss function and the corresponding statistical learning theory are still open to be explored. Thirdly, even though the hard and soft classifiers about the angle-based classification are discussed in Ref. [39], the conditional probability estimation methodology is seldom investigated. Finally, it may be very reasonable to extend the novel angle-based classification to certain fascinating and challenging settings, such as multicategory semi-supervised learning and estimation of dynamic treatment regimes.