基于改进的神经网络对航空发动机故障率预测研究

(海军航空大学 岸防兵学院，山东 烟台 264001)

0 引言

航材是飞机保障过程中的重要物质基础，是实施换件修理的必要物质条件，将直接影响到飞机的战备完好性和出动率[1]。在经历原始粗放的航材管理模式后，经济性也成为航材保障的重要因素。实际工作中，有些航材大量积压，不仅耗费资金，同时占用库房。而同时也因为部分航材缺件导致停飞。既要保证战备需求，同时也要满足经济性需求，这就要求保障过程中尽量做到精确、高效。发动机如同飞机的心脏，一方面对于飞行安全至关重要，另一方单价较贵，不能大量储存。如何预测发动机故障率，提前做好相应准备，对于提高航材保障水平具有较大意义。近年来，学者运用神经网络强大的数学模拟预测能力对航材进行预测，吴清亮在使用BP神经网络对备件的需求进行了预测[2]；李连等通过附加动量项和变步长思想对 BP 网络进行改进[4]；上述两位学者使用网络时间较早，使用原模型对部分备件进行模拟，取得初步的效果。但神经网络在很多情况下精度较差，对样本的学习能力不足，尤其是对部分航材备件，消耗量少，且服役周期较短，样本小导致预测误差较大。在此基础上，韩玉等使用粗糙集和神经网络针对舰载直升机航材消耗影响因素的非定量性以及冗余性等问题做出了优化[3]，利用粗糙集的理论知识去除冗余，筛选出主要消耗因素，之后利用神经网络建立了航材消耗模型；;陈博等在分析了灰色系统优势的基础上，对神经网络做了局部优化，提高了神经网络的鲁棒性和学习性能[5]，最后通过算例证明优化后的算法能够较好的提升预测精度。本文以某俄式发动机为研究对象，收集了3年发动机寿命记录，运用BP神经网络进行预测。通过分析样本的数据特点，针对神经网络在计算中可能产生的问题进行模型改进，使得改进后BP神经网络预测误差更小。

1 故障率模型

针对故障率进行分析预测，首先需要在收集数据的基础上，进行分析。故障率或者说是失效率，是失效发生在一定的时间段内的概率，根据用途不同，分为瞬间失效率、累积失效率和平均失效率。为方便计算，在此我们假定出厂时每个装备质量完好，在运输、储存、维护等过程中按标准完成，不存在因人为损坏的部件。

1.1 可靠度

根据GJB451A-2005定义可靠性是指“产品在规定的条件下和规定的时间内下，完成规定功能的能力”[6]。依据定义，我们将可靠度记作R(t)。假设在t=0时刻有N个装备开始工作，而到t时刻有n(t)个装备失效，即有N-n(t)个装备继续工作，则t时刻R(t)的估计值为:

(1)

1.2 累积失效概率

累积失效率是装备再时间段0至t失效的概率[6]。用公式表达为关于t的函数，记作F(t)，其表示式为：

F(t)=P{T≤t}=1-P(T>t)=1-R(t)

(2)

1.3 失效率

失效率是装备正常工作至某时刻，在该时刻后的单位时间内发生故障的概率[6]，记作λ(t)。按上述定义，失效率是失效仅发生在时间段t至t+Δt内的概率，同样是关于t的函数，其表达式为：

失效率的估计值可由下式求得:

(3)

其中:Δt为试验单位区间，Δn为Δt内失效的样品总数；Ns为到t1时刻可用样品数[5]。

1.4 平均失效率

平均失效率是装备在一个规定的时间段内总的故障数nf(t)与全体装备工作的累加时间之比[6]。 平均失效率估计值的公式为:

(4)

值得注意的是，在实际工作中，难免会有非质量原因的故障，比如飞行员操作失误等，此类数据不能用作分析装备故障率。

2 BP神经网络模型

BP神经网络是一种具有三层或三层以上的神经网络，结构如图1所示。其中包括输入层I、中间层H和输出层Y，各层之间连接权重类比为神经元细胞的神经纤维强度。当数据样本输入神经网络后，从输入层经各中间层向输出层传播，在输出层的各神经元获得网络处理过的输入响应。而后以输出数据与实际误差最小为优化目标，修正由输出层到各中间层及输入层的权值及误差参数，这种算法称为“误差反向传播算法”，即BP算法。利用误差反向传播对权值矩阵调整后，重新进行网络输出，并计算网络的输出值与真值的误差。随着这种误差反向的传播修正不断进行，网络对输入样本计算的正确率也不断提升。基于上述运算，BP网络进行不断迭代，直至误差达到理想范围或训练次数达到网络设定的最大值。

在引言中所提，目前神经网络已普遍应用于故障诊断领域，并且发挥了较大的作用。近年来，对神经网络的优化也在不断发展：一方面对模型进行优化，对激励函数、步长或者反馈机制进行完善；另一方面随着更多数学工具的发展，使用其他工具对神经网络进行优化，例如灰色系统、粗糙集等等，均使故障诊断水平有了大幅提升。但即便如此，没有一种模型能适用所有备件。一方面是备件种类庞大，在研究时难以兼顾所有；另一方面每种备件的设计寿命、使用环境、故障风险均不相同，导致故障率不同。只有针对航材特点，分析选用适当的模型才能达到最佳效果。本文使用BP神经网络对某航空发动机故障率进行预测，采用最快梯度下降法进行学习[8]。

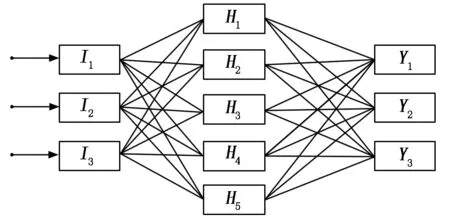
图1 神经网络结构图

传统统BP网络存在一些缺陷，网络训练时常会出现收敛慢、荡陷入局部极小值点等问题，影响预测效果[7]。本文通过改变激励函数的形式优化神经网络模型，对故障率进行拟合。

在BP神经网络中，假设输入层的节点个数为n，隐含层的节点个数为l，输出层的节点个数为m。输入层到隐含层的权重wij，隐含层到输出层的权重为wjk，输入层到隐含层的偏置为aj，隐含层到输出层的偏置为bk。学习速率为η，激励函数为g(x)。其中激励函数取Sigmoid函数[7]。形式为：

(5)

在误差反向传播的过程中，我们的目标是使得误差函数达到最小值minE，即我们使用误差梯度下降法。

3 改进的BP神经网络故障率模型

在研究发动机故障率时，由于发动机状态属于持续过程，传统BP网络拟合效果不佳。本文通过将激励函数加入模糊参数，并将参数进行训练。提高神经元对原状态的保持特性，从而减少神经元状态的错误变化，有利于提高网络的抗扰能力。参数参与学习，能更好的对样本规律进行挖掘，提高学习效率。

对故障率λi，输出函数为：

(6)

其中:c为模糊参数。

1)隐含层到输出层的权重更新:

(7)

权重的更新公式为：

wjk=wjk+ηHjek

(8)

2)输入层到隐含层的权重更新:

(9)

权重的更新公式为：

(10)

3)偏置的更新:

隐含层到输出层的偏置更新:

(11)

则偏置的更新公式为：

bk=bk+ηek

(12)

输入层到隐含层的偏置更新：

(13)

(14)

则偏置的更新公式为：

(15)

4)输出:

隐含层的输出:

(16)

输出层的输出:

(17)

误差计算:

(18)

5)模糊参数更新:

(19)

对比上文通用Sigmoid函数相比，改进后的激励函数的响应与样本数据更加紧密，具有明显的模糊特性。当权值进行改变时，模糊参数能有效减小神经元的变化，部分提高网络的鲁棒性，并增加了网络对数据样本的学习能力。网络权值的每一次更新都伴随着模糊参数的优化计算，直到网络误差达到满意范围或达到指定最大迭代次数。由于模糊网络对参数进行的优化训练，在神经元的基础上增加了有效向导，从而增强了网络对历史输入信息的学习能力，使得网络能够更充分挖掘数据样本中的规律，提高网络预测准确性[9]。

4 仿真实验

本文以某型号直升机发动机为例，该发动机设计寿命1000 h。将1000 h按照每100 h进行分段，即到每100 h内故障的发动机数，经统计故障数如表1所示。在工程实践中，常使用平均失效率，但本文考虑每个阶段航空发动机故障率，在计算时使用故障率进行考量，根据公式推导得出该型号发动机故障率在每个时间段的故障率，具体数据如表2所示。在上文中提及，本文仅排除了人为的重大故障，不同的使用环境、使用方法、保养质量等因素均会对故障率有所影响，可以使用相关文献中的工具进行具体分析，本文假定此类条件满足要求。

表1 分段故障表

表2 分段故障表

分析表1可见，该航空发动机故障率较低，相对符合浴盆曲线规律，在3个时间段内出现0值，表明该发动机可靠性较高，同时这在使用神经网络进行仿真计算时容易产生误差。多次由相对较高的数值变为0值，使应相对平稳的数据链产生较大拐点。在网络迭代时，为求得最小误差，权值会响应的增大，容易出现局部极小值。

神经网络学习过程需要处理大量计算过程，在此本实验使用MATLAB软件编程运算。由于数据样本较少，而神经网络的权值及偏置需要大量的训练次数且样本空间，因此在编程时，采用循环迭代的思路。输入变量 [0,900]区间内9个数据，激励函数从输入变量每次提取一个进行迭代训练，将前一个时间段内发动机故障率进行迭代预测下一时间段发动机故障率。在一次训练内，通过9个数据对权重及参数训练相应次数，提高了网络的准确性。[900,1000]数据用做训练完成后的预测对比值。

以0.02的学习速率进行训练，前9次训练完成后，训练后误差如表2所示。

分析运算结果，可以看出改进后的神经网络对比原网络在误差平方和减小了42.6%。使用训练过的网络在学习速率0.02时预测[900,1000]故障率，结果分别为：6.120、3.985，与真实值7.69相比，改进后的神经网络预测准确率提高了27%，运算结果如图2所示。改进后的网络比原网络更好的适应样本故障率。而原网络在低学习速率拟合不佳，收敛速度较慢，曲线平稳不能体现样本特征。

表2 0.02学习速率训练结果

表3 0.02学习速率训练结果

图2 学习速率0.02时故障率图

为进一步分析新旧网络对于样本及学习速率的关联，我们使用0.035的学习速率进行训练，前9次训练完成后，训练后误差如表3所示。

在0.035的学习速率下，改进后的神经网络对比原网络在误差平方和减小了8.6%。使用训练过的网络在学习速率0.035时预测[900,1000]故障率，结果分别为：13.495、6.509，与真实值7.69相比，原神经网络误差较大，难以采用。运算结果如图3所示。

图3 学习速率0.035时故障图

对比两次试验结果，我们可以看出，由于该航空发动机故障率较低，数据相对平稳，且0值存在较多，使得原网络在计算中陷入局部极小值问题。而随着使用时间的增加，故障率升高，前段的训练得出的权值使得预测数据过高。高学习速率较低学习速率有较好的训练效果，尤其是传统的神经网络，训练后的误差平方和与改进后的相差8.6%，但由于极值的问题，训练后的权值与理想情况差距较大，在预测n+1时间段故障率体现明显，对于样本数据拟合不佳，预测效果较差。而在激励函数中加入模糊参数，该参数参与神经网络训练，与样本有一定的关联性，在网络权值的改变中起到控制作用，避免局部极小值出现。在不同的学习速率，改进后的神经网络均体现出了一定的适应性。不仅仅是在训练过程中误差较低，更重要的是在预测时因与样本结合更为密切，预测结果更为准确。

5 结束语

通过使用收集的数据对神经网络进行训练，对比训练结果，并通过训练后的网络对数据预测，我们可以看出改进的神经网络在对于该型号发动机故障率拟合有了优化，并且故障率预测更为准确。运用该模型对于提高该备件预测准确性有一定实践意义。同时，由于样本数据容量较小，对于小样本预测问题，本文提供了一种循环迭代学习的思路。