隐式半马尔科夫模型下的变压器故障诊断方法

(1.华北电力大学 计算机系，河北 保定 071003；2.国网河北省电力公司 电力科学研究院，石家庄 050021)

0 引言

在电力系统中，变压器运行状态的变化将直接对电力系统的状态产生影响。因此，对电力变压器的健康状态进行预测，保障送变电安全，对提高电力系统的可靠性、促进电力设备基于状态的维修(condition based maintenance, CBM)具有重要意义。为保障变压器的正常和安全运行，对其健康状态的监控与故障预测技术越来越受到变压器运维人员和研究学者们的重视[1]。在实际应用中，变压器在故障产生前，通常会经历一系列的退化状态，当积累到一定程度时，会最终导致变压器故障[1]。如何正确的划分和识别变压器从正常状态到故障状态之间的状态序列，是故障诊断研究中非常关键的一步，也是能够得到较高诊断可靠度的前提条件之一[2-3]。

近年来，已有大量针对电力变压器状态评估与故障诊断的研究成果报道[4-6]，但由于变压器是一类内部结构复杂、运行工况与外在环境多变的设备，因此，寻找一种有效的方法对其故障演化规律进行清晰的刻画较为困难。例如，有研究者开始把HMM模型引入到基于状态的设备维修和故障诊断领域中来，取得了良好的效果[7-9]。HMM在设备状态识别领域的应用是对设备历经的多个健康状态分别建立并训练对应的HMM，实现对状态的划分。文献[10]将HMM应用于机械设备故障诊断领域，通过对振动信号的学习，实现了基于状态的维修。文献[11]将HMM应用到发电机转子的状态识别中，描述了设备运行状态的变化。文献[12]对旋转机械的变速过程进行HMM建模，在建模过程中采用了多个观测变量进行分析，得到了较好的诊断结果。但这些研究只使用了标准HMM技术，因为HMM的状态持续时间遵循指数分布，所以模型对时间结构的描述不够精确，建模过程中未考虑设备的历史状态信息，为充分利用马尔科夫过程的特点，需要对HMM模型中对历史状态不敏感的缺点进行改进。

隐式半马尔科夫模型(hidden semi-markov models, HSMM)将历史状态信息纳入计算过程，能够克服 HMM对历史状态信息不敏感的局限性[13]。本文尝试在变压器故障诊断中，对HSMM模型引入“微状态-宏状态”的对应关系来描述变压器健康状态的转移。最后使用变压器DGA故障数据对HSMM模型进行训练，并通过实验来验证模型的可靠性及准确性。

1 HMM基本理论

1.1 基本理论

一个HMM模型可用下列参数描述[9]：

(1)N为模型中Markov链的状态数目。记N状态为：s1，s2，...，sN，记t时刻Markov链所处的状态为qt，显然qt∈(s1，s2，…，sN)。

(2)M为一个隐状态产生的观测值种类数量。记M个观测值为o1，o2，...，oM，记t时刻的观测值为ot，其中，ot∈(o1，o2，...，oM)。

(3)π为初始概率分布矢量，π=(π1，π1，…，πN)。πN初始时刻时，模型处在该状态的概率。其中:

πi=P(qt=si)，1≦i≦N

(1)

(4)A为状态转移矩阵，A={aij}N*N。其中:

aij=P(qt+1=si|qt=si)，1≦i，j≦N

(2)

(5)B为观测值概率矩阵，B={bjk}N*M。其中:

bjk=P(ot=vk|qt=sj)，1≦j≦N，1≦k≦M

(3)

这样可以记HMM为λ=(N，M，π，A，B)，因为在模型中，各个参数之间又具有一定的关联，N和M确定之后才能计算A和B，所以HMM可简写为λ=(π，A，B)。

HMM在实际应用中的3个相关基本问题及算法描述如下[11]：

(1)评估问题(“前向-后向”算法)：在给定的观察序列o=o1，o2，...，oM和参数组为λ=(π，A，B) 的HMM中，该观察序列出现的概率是多少？

(2)解码问题(Viterbi算法)：在给定的观察序列o=o1，o2，...，oM和参数组为λ=(π，A，B) 的HMM中，隐藏状态序列s=s1，s2，...，sN生成所给出的观察序列的概率是多少？

(3)学习问题 (Baum-Welch算法)：观察序列确定的情况下，如何设定HMM中的参数，如：初始概率分布(π)、状态转移矩阵(A)等，才能够使得HMM输出该观测序列的概率最大？

HMM是一个双重随机过程，它可以在概率统计学的基础上解答上述3个问题。HMM的参数λ=(π，A，B)可以由Baum-Welch算法从观测到的DGA数据中估计出来，由估算出的HMM组成分类器，可以实现对观测序列的分类。具体流程如图1所示。

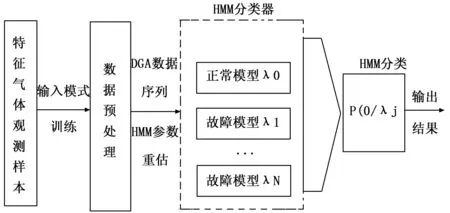
图1 HMM故障诊断流程图

1.2 HMM初始模型选取

在使用HMM对变压器运行状态进行建模时，将初始模型的隐状态数量设定为4，并采用均匀选取的办法对模型的观测值概率矩阵选取进行确定。HMM的初始形态如图2所示。模型中变量之间的依赖关系用箭头来表示，箭头上的数字表示此次状态转移的概率，由圆圈中的数字表示HMM模型中不同的隐状态。根据HMM模型的基本理论可知，每个隐状态都可能产生多个观测值，图2中的o1，o2，...，oT都表示为离散的观测值序列。

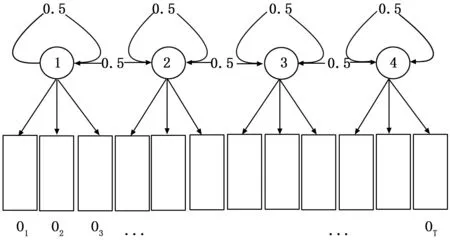
图2 HMM变压器故障模型

当建立了HMM的初始模型后，就可以采用Baum-Welch算法进行计算，为变压器的每个故障类型训练出相应的HMM，从而建立起面向变压器的HMM分类器。

2 对HMM的适用性改进

2.1 HMM的局限性分析

在HMM研究和应用领域的相关内容中可以归纳出其模型的局限性，主要表现为以下几点[14]：

(1)HMM状态驻留概率遵循指数分布。即系统在状态i持续时间为d的概率为：

(4)

式中，aii表示系统驻留在状态i的概率。根据公式(4)的表示，随着驻留时间d的增加，Pi(d)呈指数下滑，这也与实际情况不符合。

(2)HMM假设模型中各观测变量之间互不影响，即观测序列产生仅与当前所处的状态有关：

P(o1，o2，...，ot|s1，s2，…，st)=P(ot|qt)

(5)

o1是由s1生成的，o2是由s2生成的，但是s2的形成受s1影响，所以o1和o2也一定有联系。但是为了研究和应用方便，就假设s1和s2不独立，但o1和o2独立。在实际的变压器DGA运行过程中，各个状态之间能够相互转化，所以这个假设与实际情况不符。

(3)HMM模型中，马尔可夫过程具有齐次性，表现在变压器的状态转移中即为——状态转移矩阵确定后，不会随变压器状态的变化而变化。在实际情况中，随着变压器运行状态的不断改变，其各个状态之间的转移概率肯定会不断变化。

2.2 改进思路

针对上述局限性，目前的改进方法就是根据应用场景的不同，适当放宽HMM模型的假设条件，主要思路如下：

(1)在传统的HMM 结构上加入时间要素，使状态转移矩阵能够根据历史状态信息进行改变，打破马尔科夫过程的齐次性。

(2)在HMM模型各个状态转移概率的计算过程中，加入历史状态的变化量，来描述各个状态之间的跳转信息。该方法具有较强的适应性，但是每次状态转移过程的计算与建模较为复杂。文献[15]表明，在基于HMM的手写字体识别系统中，因为手写字母的分割处理程序本身具有极强的不确定性，所以使用结合历史状态的模型来实现手写字体的识别是切实可行的。

(3)针对HMM的观测序列输出仅与当前状态有关的假设，可将观测序列之间的依赖性加入建模过程中。自回归隐马尔可夫模(Auto-Regressive Hidden Markov Model, ARHMM)通过AR模型计算的观测值概率矩阵B={bjk}N*M，其中，bjk=P(st=sj|ot=oj)，反映了状态st和观测序列ot之间的统计对应关系：

bjk=P(sj|ot=oj)=N(sj|∑ak(i)ot-i|∑k)

(6)

式中，N(·)表示高斯函数，∑k表示高斯分布的估计方差，通过统计学将状态与观测序列之间建立关系，实现了观测序列之间的依赖性。文献[16]通过ARHMM 对工业控制过程的数据进行异常检测，提升了检测精度和抗干扰能力。

3 基于HSMM的变压器健康预测方法

3.1 HSMM的构造

目前基于HSMM故障诊断的应用对象主要以旋转机械居多，通过对其工作过程中的振动信号进行建模分析，实现对其健康状态的划分，旋转机械振动信息采集的连续性较强[17]。但是变压器的故障数据，如DGA数据的采集通常为间隔操作，变压器健康状态的持续时间也远较机械设备等更长久，具有宏观上的离散性。因此，本文结合变压器DGA数据采集特点及状态演变规律，引入“微状态-宏状态”的对应关系来描述变压器的运行过程，将变压器历史状态信息纳入建模过程中，以提升模型准确率。

变压器的运行状态分为正常状态和故障状态，故障类型分为放电性故障和过热性故障，其中放电性故障分为：低能放电、高能放电；过热性故障分为：中低温过热(温度≦700 ℃)、高温过热(温度≧700 ℃)[18]。其中两种故障特性都包含的有：低能放电兼过热和高能放电兼过热。本文所采用的HSMM是在传统HMM结构上加入了时间要素，为变压器故障诊断提供更好的建模和数据分析能力，具体如下：

针对变压器的各个健康状态，使用各类DGA故障数据对HSMM进行训练，与HMM不同的是，HSMM中的 “宏状态”对应变压器的各个健康状态。

HSMM与传统HMM的不同还体现在状态与观测值的产生方式上，传统HMM 的一个状态仅产生单个观测值，但HSMM的一个状态会产生一个由多次观测值组成的观测值片段。本文将HSMM中隐状态一次产生的观测值被称为“微状态”，由连续多次的观测值组成的片段称为“宏状态”。其对应关系如图3所示。在HSMM中s表示变压器的隐状态，o表示由采集的DGA数据处理得来的观测序列。

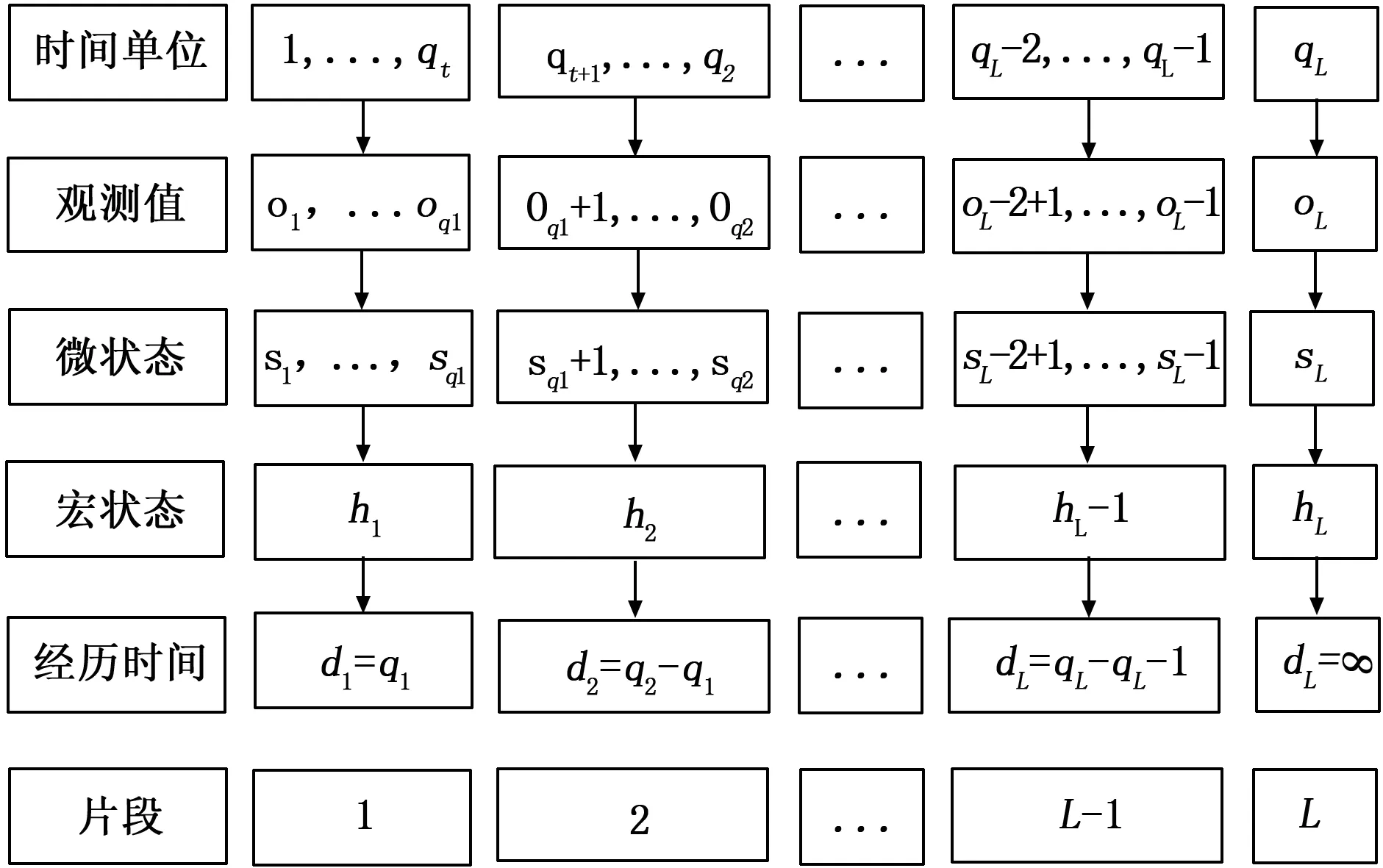
图3 HSMM模型示意图

如图3所示，值为oqi-1，...，oqi的观测序列，对应的微状态为sqi-1，...，sqi，这个微状态序列对应HSMM模型中相同的宏状态即hi。

HSMM可表示为λ=(π，A，D，B)，其中，π表示初始状态分布，A表示状态转移矩阵，D表示状态持续时间分布，B表示观测值概率矩阵。在HSMM模型中具有多个微状态，这些微状态的转换不具有马尔科夫性，而模型中宏状态之间的转换是符合马尔科夫过程的，状态转移矩阵(A)用来描述这些隐状态之间的转换：

P(hql=j|hql-1=i)=aij

(7)

3.2 基于HSMM的变压器故障诊断流程

为了能够使HSMM模型识别出变压器在运行过程中不同的状态，所以在训练模型时采用各种变压器DGA故障数据，为所有变压器的正常状态和每个故障类型各训练一个单独的HSMM模型，从而建立起变压器故障的HSMM分类器。如图4所示。

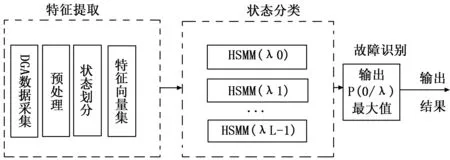
图4 HSMM故障诊断示意图

基于HSMM的变压器故障诊断流程，由特征提取、状态分类和故障识别3个部分组成。其中，状态分类是该流程中的关键步骤，其HSMM的计算过程如下：根据观测序列利用“前向-后向”算法求解最优模型λ，采用Baum-Welch算法训练模型，得到输出该观测序列概率值最大的模型参数。在模型中每个变压器的运行状态都对应一个训练好的HSMM，将观测序列依次代入每个HSMM模型中进行计算，得到该观测序列的P(o|λ)，即为发生该故障的概率。

4 算例分析

在电力变压器的诊断分析环节中，DGA分析技术的数据采集方便，分析结果也较为准确，所以近年来的变压器健康管理和DGA技术紧密结合[19]。在运行过程中如果变压器发生过热或放电性故障时，会使得内部固体绝缘材料和绝缘油如绝缘纸板、电缆纸等加速发生分解，产出气体。主要气体有氢气(H2)、烃类气体如：甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、一氧化碳(CO)、二氧化碳(CO2)等。在这7种气体中，因为变压器内部受到空气中二氧化碳渗入的影响较大，故其不能够灵敏的反应运行状态变化，所以一般不将二氧化碳(CO2)作为判断故障的特征变量。当变压器运行状态发生改变时，一氧化碳(CO)在绝缘油中的溶解浓度要远大于其他特征气体，在HSMM建模过程中容易掩盖其他油中溶解气体对于模型计算的影响。为了简化问题，同时结合实际情况，将用于HSMM建模的特征变量定为5个，即氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)，且只考虑样本之间的关系。由此可得到特征气体的矢量表达式：

X=[H2，CH4，C2H6，C2H4，C2H2]

(8)

先对DGA数据进行归一化，使数据限制于[0, 1]之间。由于H2、CH4、C2H6、C2H4、C2H2这几种特征气体都是可燃性气体，通常将这些DGA特征气体含量总和称为可燃气体总量(TCG)。通过将这5种特征气体变量与TCG的比值实现DGA数据的归一化处理，即以H2/TCG、CH4/TCG、C2H6/TCG、C2H4/TCG、C2H2/TCG作为归一化的DGA数据，从而将DGA数据限制在0到1之间。

当发生放电性故障时，若CH4/H2>1，则同时伴随有过热性故障的发生，即此时变压器的运行状态出现放电兼过热性故障；当CH4/H2≦1时，一般认为是纯放电性故障。当训练HSMM变压器故障模型时，我们将放电性故障和放电兼过热性故障合为一种故障类型，即将变压器的运行状态由7类合并为5类：正常、中低温过热(温度≦700℃)、高温过热(温度≧700℃)、低能放电，高能放电。合并运行状态，可以提升HSMM的训练速度和正确率。例如，若输入的特征气体观测矢量为x=[85.9，66.0，15.3，25.7，6.3]，则HSMM模型各状态的识别结果输出如表1所示，其发生高能放电故障的概率是98.45%。

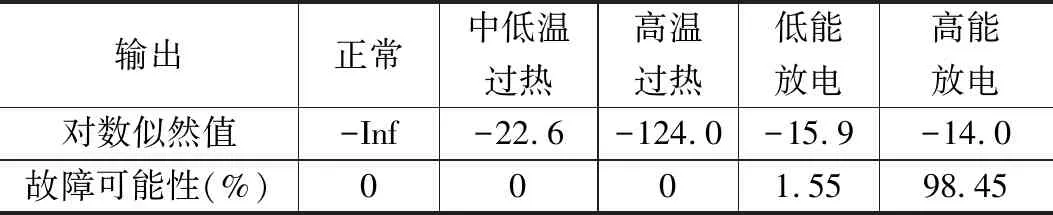
表1 HSMM输出

表1中的对数似然值就是由HSMM对观测矢量X进行分类得到的对每个状态的logP(o|λ)，其中Inf表示无穷大，HSMM输出的对数似然值越大，则表示此故障的发生概率就越大。

我们从相关文献和资料收集到的样本中选出变压器运行过程中每个状态各15组数据，这75组数据未在模型中参与训练过程，作为HSMM的输入矢量进行分类测试。在本算例实验中，因为变压器运行状态共有5种，所以设定HSMM模型中隐藏状态数目为5；因为初始值的选取对于训练结果的影响不大[19]，所以对于HSMM的初始模型π，我们采用均匀选取。设置训练过程中的收敛值0.0001，最大迭代次数为100。在一开始的训练过程中，随着迭代次数的增加，各个状态输出的对数似然值也逐渐加大，即状态识别的正确率也在逐步提高。各个状态输出的对数似然值曲线在10次后趋于平稳，总体训练过程的迭代次数都在15次之内，训练过程如图5所示。

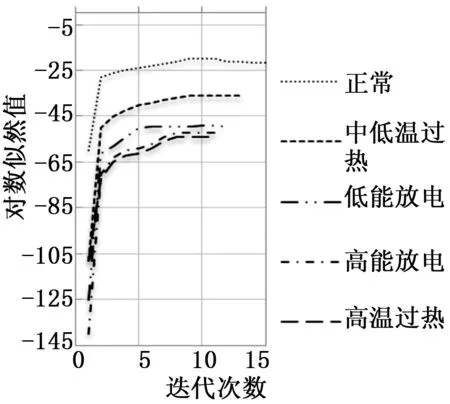
图5 5种状态HSMM的训练曲线

当各种故障类型的HSMM建立以后，就可以使用图4所示的方法进行故障识别。为了能够直观的了解HSMM变压器诊断方法的效果，把这75组数据用传统HMM方法进行诊断，并和本文所述的诊断方法进行比较。从本次实验的结果可以看出，相较于传统HMM方法， HSMM方法正确率更高。HSMM对于每个故障类型的划分都要比HMM准确。测试结果如表2所示。

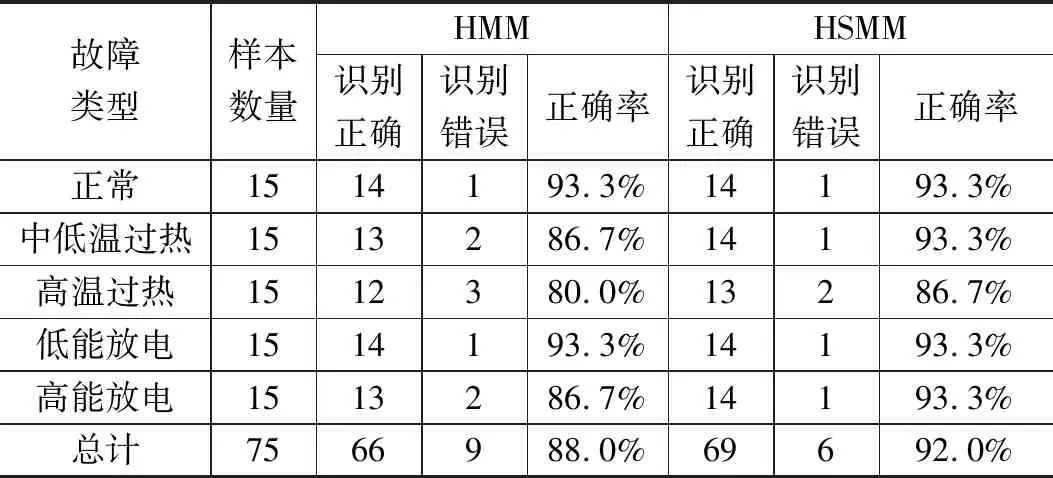
表2 暂态运动各自由度稳态误差

5 结束语

本文针对传统HMM在电力设备故障诊断中的局限性，通过引入“微状态-宏状态”，考虑变压器运行过程中的历史状态对于状态转移的影响，给出了一种基于HSMM的变压器故障诊断流程，并采用DGA数据进行了算例分析，结果验证了模型的有效性，也更加符合变压器实际运行状态。