基于T-S模糊模型的简单互联电力系统事件触发控制
(海南电网有限责任公司海口供电局,海南 海口 570100)
近几年,随着我国国民节能环保意识的不断提高,越来越多的人选择购买与使用电动汽车(Electric Vehiche,EV),全国各地也随之建立了大量的充电站,仅2014年我国电动汽车销量就达到7.5万辆,2015年,我国20多个示范城市及周边区域建立充电桩达40万个,充换电站达2000个。电动汽车行业的快速发展有效缓解了我国石油能源紧缺与环境污染问题,但同时也对电力系统带来了一定的挑战。对于电力系统而言,电动汽车在充电时作为负荷,在使用时又可看作分布式电源,因此,大量电动汽车的充放电对于电力系统来说有着难以预计的干扰,如果在高峰时期进行充电将造成电网负荷“峰上加峰”,对电力系统的稳定性将造成严重影响[2]。
在控制系统的设计中求得一个控制器是其基本任务,一个优良的控制器可以使闭环系统保持稳定性和良好的系统性能。要保证闭环系统首先是稳定的,一个不稳定的系统是无法正常工作的,在稳定基础上,再寻求系统的性能,这样的控制系统才具有实际应用价值。若想设计控制系统,首先要建立系统的模型,然而,从理论上分析没有一个数学模型可以准确地表达其相应的系统,这时就需要采用一个更为精准或更为有效的模型来进行研究,模糊模型就具备这种优势[3,14]。
在模糊领域研究中发现,非线性系统可以通过T-S模糊模型进行研究,其结果往往比数学模型所研究的成果要更加精准和可靠,此外,模糊控制对系统中干扰和波动的影响有很好的控制能力。在T-S模糊控制中,控制器是核心,决定着系统的性能,采用事件触发将使控制器功能得到提升,有助于减少传输数据、缓解网络压力、提升系统工作效率[5,15]。
1 简单互联电力系统模型
简单互联电力系统的数学模型如下[1]:
(1)
式中:δ(t)为等值发电机q轴电势之间相对角度;ω(t)为发电机转速;Pm和Ps分别为发电机机械功率和电磁功率;F为等值转动惯量;E为等值阻尼系数;Pe为扰动功率幅值;β为扰动功率频率。设δ(t)、ω(t)为系统的状态变量。
2 建立T-S模糊模型
在式(1)中,令δ(t)=x1(t),ω(t)=x2(t),则sinδ(t)=sinx1(t)。再令z1(t)=-Pssinx1(t)/F,w(t)=Pecos(βt)/F,其中x1(t)∈(-π/2,π/2),通过扇区法可将-Pssinx1(t)/F线性化,由图1可以看出扇区[b1,b2]由b1x1和b2x1两条线组成,斜率分别是b1=1和b2=0.451。因此z1(t)可写成如下形式[6]:
(2)
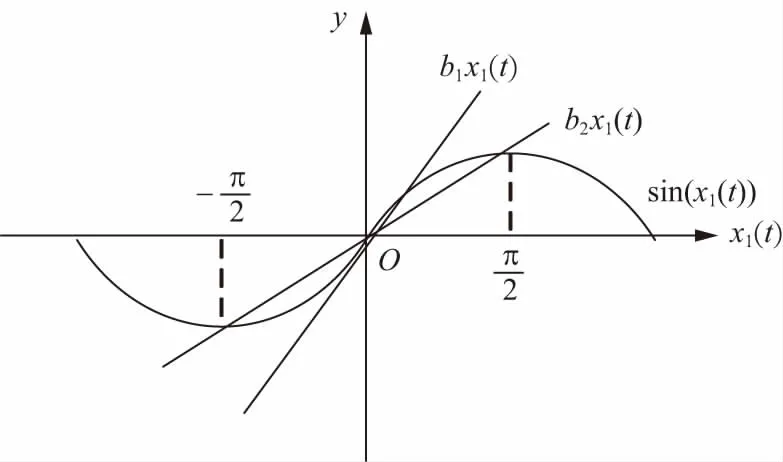
图1 sinx1(t)的扇区图
根据模糊隶属度函数性质可得
μ1(z1(t))+μ2(z1(t))=1
(3)
根据式(2),可得
线性化后可得非线性系统的表达形式如下:
(4)
式中:u(t)∈R1为励磁控制是系统的控制输入,x(t)∈R2为状态变量,w(t)∈R1为系统的干扰向量。令x2(t)∈[-1,1],则式(4)可以写成
(5)

参数分别取F=100,Ps=100,E=2,Pm=20,β=1。根据式(5)可得到如下模糊规则。
规则1:如果z1(t)大约是1,则
(6)
其中
规则2:如果z1(t)大约是0,则
(7)
其中
Al∈R2×2是状态矩阵,Bl∈R2×1是输入矩阵。Fg(g=1)为模糊集,z(t)=z1(t)是可测的系统变量,即前件变量。Fg((zg(t)))是表示zg(t)关于模糊集Fg的模糊隶属函数。
采用单点模糊化、乘积推理和平均加权反模糊化,简单互联电力系统的全局模糊模型为
(8)
3 控制器的设计
对于连续状态模糊T-S模型,采用并行分布补偿(PDC)技术结合事件触发设计简单互联电力系统的控制器。第h个控制规则如下[4]:
如果z1(t)大约是F1,则
u(t)=Khx(tk)
采用单点模糊化、乘积推理和平均加权去模糊化,则可以得模糊分散控制器如下:
(9)
式中:Kh为确定的静态增益反馈矩阵。事件触发采样模式中k是一个正整数,表示事件触发的次数。tk是事件触发的离散时间的转换形式,即第k次事件触发时的时间。事件触发公式的形式如下[7]:
(10)
定义事件触发形式为
e(t)=x(tk)-x(t),t∈[tk,tk+1)
(11)
由(9)式和(11)式可得到
(12)
且t是距离第k次事件触发的时间,而ρ是用户自己设定的一个正数参数,He和Hx是用户自己设定的两个矩阵,事件次数被形成如下形式:
式中:时间序列{tk}k∈N表示整体控制器(9)被更新。
由(6)式和(12)式,可得到非线性子系统的模糊模型闭环方程为
(13)
4 H优化控制判据
在状态不完全可测的情况下,针对简单互联电力系统稳定性判断问题,结合建立的模糊模型,并基于李雅普诺夫稳定性理论和模糊逻辑结合LMI技术,同时引入事件触发模式,求得状态反馈控制器的存在条件,确保闭环系统李雅普诺夫意义下的渐近稳定性,给出简单互联电力系统稳定性判断问题状态反馈控制器的控制方法。
引理1:给定适当维数的常数矩阵X和Y,对于任意的ε>0,使下列不等式成立[8]:
XTY+YTX≤εXTX+ε-1YTY
引理2:给出任意一个对称矩阵S=ST[9]:
式中:S11∈Rr×r,S12、S21、S22是已知的矩阵。则以下三个等式等价且均成立:
通过上述分析以将简单互联电力系统转换成T-S模糊模型,接下来要将模糊模型进行优化控制,采用H控制进行优化控制,首先进行H的性能分析,H在零初始状态下的性能指标为[10]
(14)
式中:γ为常数,已知V(x)=xΤ(t)Px(t)是李雅普诺夫函数,将式(14)后面加一个V(x)在减去一个V(x)可得到
(15)
这时将V(x)带入积分内可得到
(16)
定理1:在非线性系统(1)中,如果Q=QΤ是如下不等式(17)的公共解,则模糊分散控制器(9)使得整个非线性简单互联电力系统在李雅普诺夫意义下稳定且H性能指标得到保证。
(17)
证明:取系统李雅普诺夫函数V(x)=xΤ(t)Px(t),求V(x)对时间的导数,可得[11]
(18)
(19)
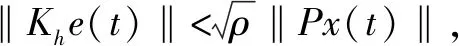
(20)
根据式(19)和式(20)可以得到
(21)
通过式(19)和式(21)可得到
(22)
根据式(22)可得
由以上推导,可得到
(23)
要确定式(9)中的模糊控制器实现式(14)中的H性能指标。通过之前证明,将式(13)关于z(t)的部分和式(23)代入式(16)后可得到如下形式:
(24)
整理之后为
(25)
因为当t=时,V(t)趋近于0,所以式(25)可写成式(26)。
(26)
则可以得到如下矩阵:
整理后,存在一个状态反馈H控制,当且仅当存在一个对称正定矩阵P,使得以下的矩阵不等式成立
(27)
根据变换式(27)可写成式(28)。
(28)
根据引理2,式(28)可写成式(29)。
(29)
上式中存在未知矩阵变量P,因为该矩阵变量是以非线性的形式出现在这个矩阵不等式中的,因此,若直接从以上矩阵不等式中求出P的解是很困难的。但是,可以采用一个适当的变量去替换它,将上式转化为一个等价的关于新的变量的线性矩阵不等式,从而可以应用求解线性矩阵不等式的有效工具来求解这组新变量,进而得到P的值。
因此,可将式(29)左边的矩阵分别左乘和右乘矩阵diag[P-1,I,I,I],可得到[12]
再令Q=P-1,可得
(30)
令Hh=KhQ,式(30)可写成式(17)。
证明完毕。
5 数值仿真
根据上述推导与证明,本文以简单互联电力系统进行仿真,假定全部状态是可测的,利用上述的模糊T-S规则式(6)和式(7)分别对简单互联电力系统在工作点z1(t)=1、z1(t)=0处局部线性化,由定理1,用MATLAB的LMI工具箱中的函数“feasp”解式(17)中的可行性问题。得到[13]

其控制器矩阵为
K1=[-0.9490 -1.6141]
K2=[-1.4980 -1.6141]
当初始条件为x0=[0.09 0.09]Τ、仿真步长为0.01s,ρ=12时,简单互联电力系统在模糊分散控制器式(9)作用下的闭环状态响应曲线见图2,控制输入曲线见图3,优化输出曲线见图4,事件触发信号曲线见图5。
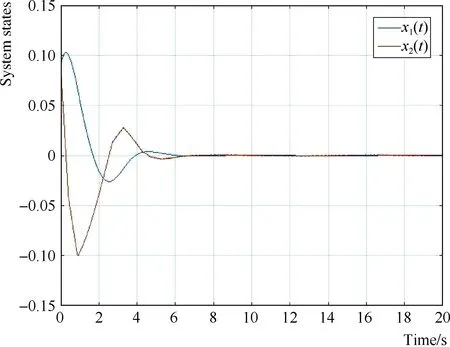
图2 简单互联电力系统的状态响应

图3 简单互联电力系统的控制输入
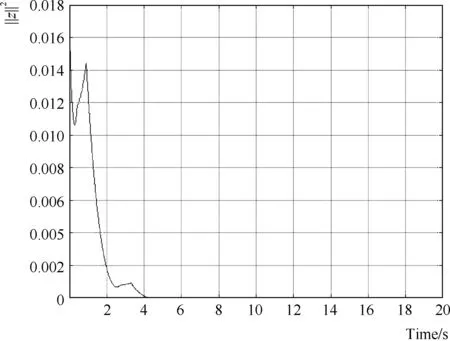
图4 简单互联电力系统的优化输出响应

图5 简单互联电力系统的事件触发信号
6 结 论
本文全面推理了在状态可测情况下含有干扰的简单互联电力系统稳定性的充分条件,实现电力系统的H优化控制,并采用数值仿真的例子说明了方法的有效性。首先采用T-S模糊模型进行建模,根据李雅普诺夫稳定性理论、事件触发理论及H优化控制理论,基于线性矩阵不等式(LMI),利用并行分布补偿(PDC)技术,证明出保证该电力系统稳定性的充分条件,实现电力系统的H优化控制,然后,给出该系统控制器的设计方法。从仿真中可以看出,运用本文提出的设计方法能有效地实现这类电力系统的稳定性判据。

