光伏发电最大功率点跟踪系统设计及潮流计算

廖勇过 李峤

摘 要：由于光伏阵列的输出特性受光照强度和环境温度等外界条件的影响较大，且呈非线性关系。文章首先在Simulink环境下建立了光伏阵列及其MPPT的仿真模型进行仿真处理，然后根据对仿真结果的分析，此模型能够稳定地追踪最大功率，建立稳定的工作状态。最后，采用MPPT控制得到的光伏发电系统的多组输出数据求解数学期望，将期望值经理想化无损逆变后送入改造的IEEE14节点系统，采用牛顿—拉夫逊法进行潮流计算，得到改造的IEEE14节点系统的所有节点数据。

关键词：光伏阵列；最大功率；建模仿真；潮流计算

随着传统化石能源的日渐枯竭以及人类对环境保护意识的增强，找到一种无污染的可再生能源作为传统化石能源的替代品显得尤为迫切。太阳能光伏发电是一种清洁高效的发电方式，其具有不受地面布局和高度落差等地理因素的影响，电能转换过程简单，无废弃污染物排放的特点，从而应用广泛[1]。

太阳能光伏发电主要是利用太阳能电池板的光生伏打效应进行光能与电能的转换[2]。光伏阵列的输出特性（电压、电流、功率）会随外界环境因素的改变而改变。其中，光照强度和环境温度这两个因素对输出特性的影响较大。因此，建立光伏阵列的数学模型和仿真模型，能够分析得到随着外界条件的改变，光伏阵列的输出特性变化的规律，进而在一定的MPPT系统下实现最大功率点跟踪，使光伏阵列输出最大功率。

1 光伏阵列的数学模型及MPPT控制

1.1 光伏阵列的数学模型

1.2 最大功率追踪

在光伏发电系统中，光伏阵列的输出功率除了与光伏电池的内部特性有关外，还与外界环境如光照强度、温度和负载等主要干扰因素有关。而光伏阵列无论外界条件怎样变化，都能始终工作在最大功率附近的过程就叫作最大功率点跟踪。因此，本文重点研究环境温度和光照强度对光伏阵列输出功率的影响。由于光伏阵列的输出功率与环境温度和光照强度呈现非线性函数关系，而且光伏阵列的工作点会随着负载电压的变化而变化。MPPT的作用就是采用DC-DC直流变换电路和寻优控制程序，使得无论外界条件怎样变化，始终让光伏阵列工作在最大功率点附近，得到最大输出功率。其中使用位于光伏阵列与负载之间的DC-DC直流变换电路的目的是进行负载匹配，通过改变直流变换电路中开关管的导通和关断，就能对光伏阵列的最大功率点进行调配，使系统始终工作在最大功率点，输出最大功率。

2 建模与仿真

2.1 光伏阵列的建模与仿真

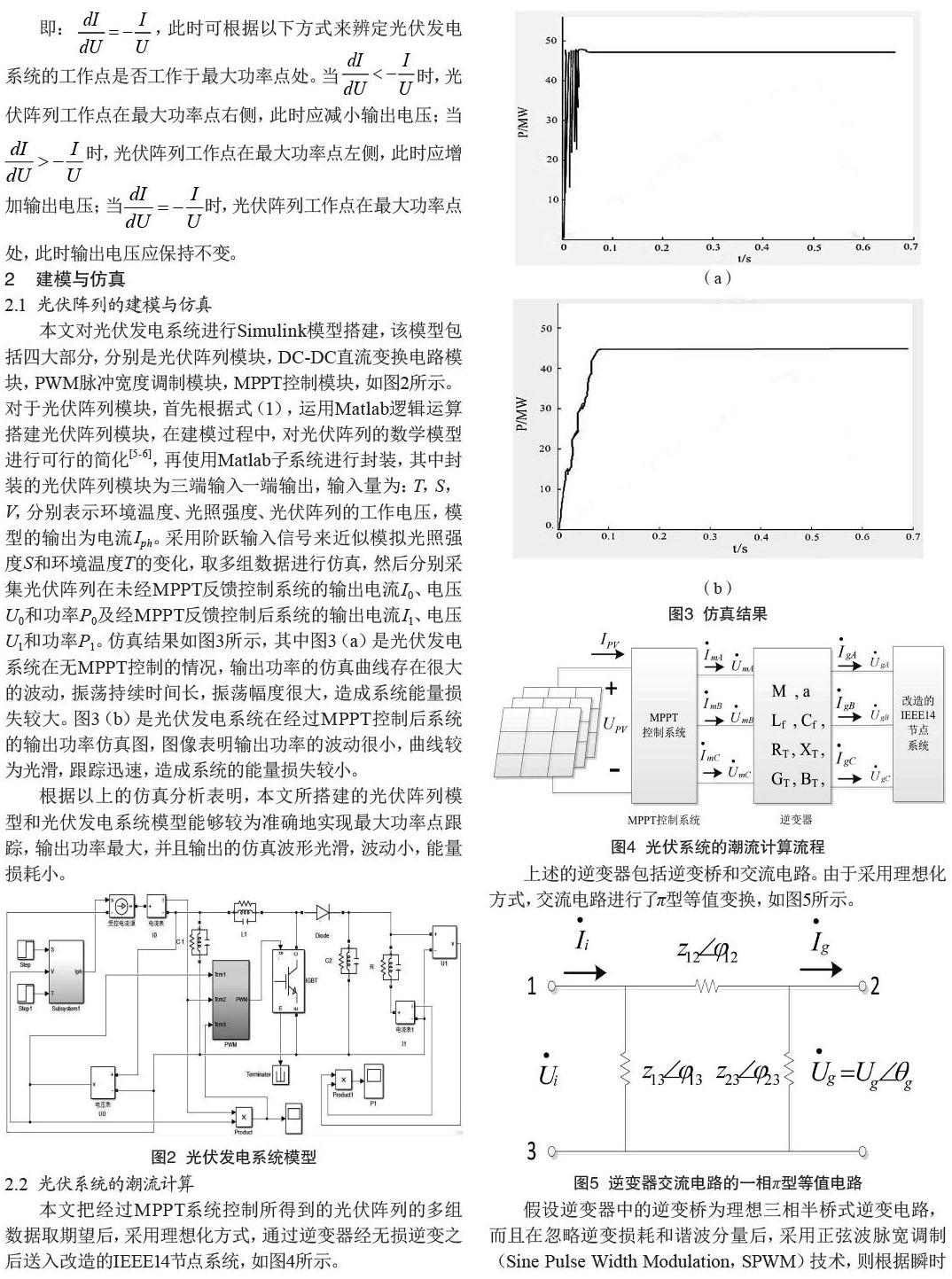
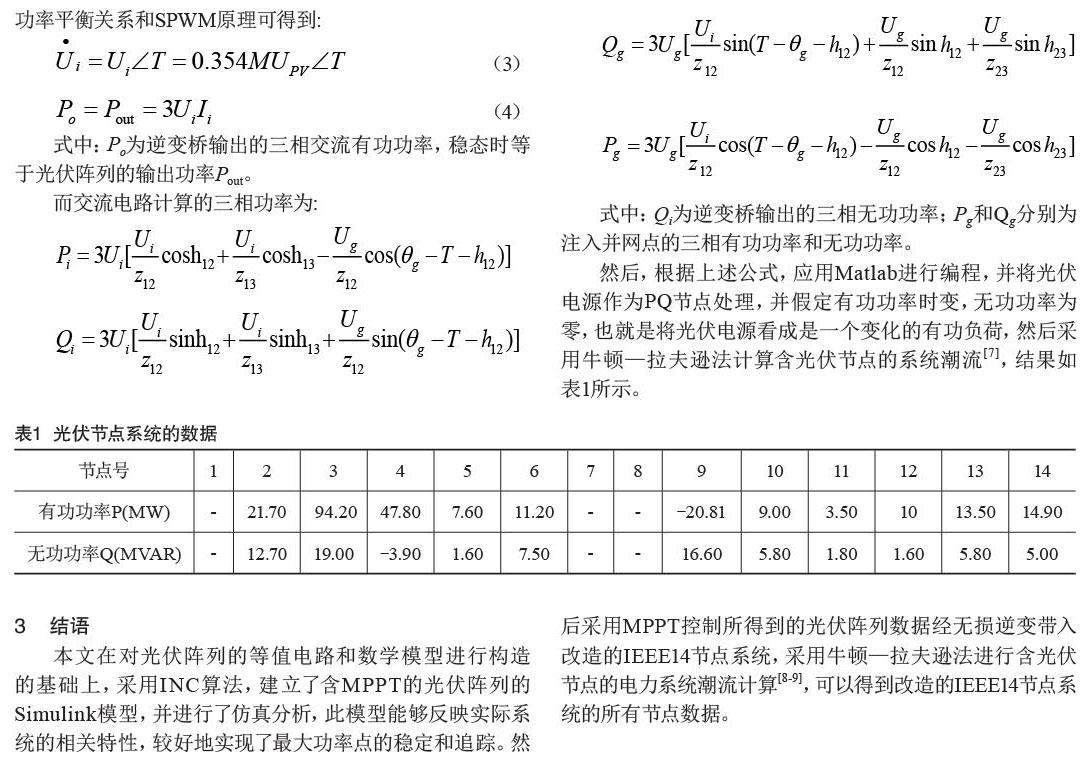
本文对光伏发电系统进行Simulink模型搭建，该模型包括四大部分，分别是光伏阵列模块，DC-DC直流变换电路模块，PWM脉冲宽度调制模块，MPPT控制模块，如图2所示。对于光伏阵列模块，首先根据式（1），运用Matlab逻辑运算搭建光伏阵列模块，在建模过程中，对光伏阵列的数学模型进行可行的简化[5-6]，再使用Matlab子系统进行封装，其中封装的光伏阵列模块为三端输入一端输出，输入量为：T，S，V，分别表示环境温度、光照强度、光伏阵列的工作电压，模型的输出为电流Iph。采用阶跃输入信号来近似模拟光照强度S和环境温度T的变化，取多组数据进行仿真，然后分别采集光伏阵列在未经MPPT反馈控制系統的输出电流I0、电压U0和功率P0及经MPPT反馈控制后系统的输出电流I1、电压U1和功率P1。仿真结果如图3所示，其中图3（a）是光伏发电系统在无MPPT控制的情况，输出功率的仿真曲线存在很大的波动，振荡持续时间长，振荡幅度很大，造成系统能量损失较大。图3（b）是光伏发电系统在经过MPPT控制后系统的输出功率仿真图，图像表明输出功率的波动很小，曲线较为光滑，跟踪迅速，造成系统的能量损失较小。

根据以上的仿真分析表明，本文所搭建的光伏阵列模型和光伏发电系统模型能够较为准确地实现最大功率点跟踪，输出功率最大，并且输出的仿真波形光滑，波动小，能量损耗小。

2.2 光伏系统的潮流计算

本文把经过MPPT系统控制所得到的光伏阵列的多组数据取期望后，采用理想化方式，通过逆变器经无损逆变之后送入改造的IEEE14节点系统，如图4所示。

上述的逆变器包括逆变桥和交流电路。由于采用理想化方式，交流电路进行了π型等值变换，如图5所示。

然后，根据上述公式，应用Matlab进行编程，并将光伏电源作为PQ节点处理，并假定有功功率时变，无功功率为零，也就是将光伏电源看成是一个变化的有功负荷，然后采用牛顿—拉夫逊法计算含光伏节点的系统潮流[7]，结果如表1所示。

3 结语

本文在对光伏阵列的等值电路和数学模型进行构造的基础上，采用INC算法，建立了含MPPT的光伏阵列的Simulink模型，并进行了仿真分析，此模型能够反映实际系统的相关特性，较好地实现了最大功率点的稳定和追踪。然后采用MPPT控制所得到的光伏阵列数据经无损逆变带入改造的IEEE14节点系统，采用牛顿—拉夫逊法进行含光伏节点的电力系统潮流计算[8-9]，可以得到改造的IEEE14节点系统的所有节点数据。

[参考文献]

[1]牛成东.微电网光伏发电系统控制策略研究[D].保定：华北电力大学，2017.

[2]赵朝会.光伏发电技术的研究现状和应用前景[J].上海电机学院学报，2008（2）：104-109.

[3]苏建徽，余世杰，赵为，等.硅太阳能电池工程用数学模型[J].太阳能学报，2011（4）：409-412.

[4]杨浩.光伏阵列在阴影条件下输出特性分析[J].江汉大学学报（自然科学版），2018（5）：395-403.

[5]刘邦银，段善旭，康勇.单相单级并网光伏发电系统中二次功率扰动的分析与抑制[J].太阳能学报，2008（4）：407-411.

[6]陈中华，赵敏荣，葛亮，等.硅太阳能电池数学模型的简化[J].上海电力学院学报，2006（2）：178-180.

[7]王一波，伍春生，廖华，等.大型并网光伏发电系统稳态模型与潮流分析[J].清华大学学报（自然科学版），2009（8）：1093-1097.

[8]刘军.光伏发电系统最大功率点跟踪算法的研究[J].青岛科技大学学报（自然科学版），2012（1）：78-81.

[9]张晔，顾勇，杜春晖，等.基于MATLAB的光伏电池最大功率追踪建模与仿真[J].科学技术创新，2018（15）：39-40.