预应力CFRP板加固混凝土梁的挠度计算方法

陈 华,王鹏凯,谢 斌,黄裕勇

(1.广西科技大学 土木建筑工程学院,广西 柳州 545006;2.南宁学院 土木与建筑工程学院,南宁 530200)

CFRP板具有轻质、高强、耐腐蚀的特性,使其在结构加固中得到广泛应用[1-2]。现有的加固方法有两种:普通粘贴法和预应力加固法。但普通表层粘贴法由于CFRP板的弹性模量与钢筋相当,在正常使用阶段其高强性能无法发挥,CFRP板梁变形能力影响较小[3-4],可通过对CFRP板施加预应力减小梁在正常使用阶段的挠度来克服这一缺陷。国内外相关论著及规范研究发现,预应力混凝土梁的挠度计算方法主要有:直接双线性法、有效惯性矩法及曲率积分法3种[5-6]。本文通过对3种方法的研究,总结出一套关于预应力CFRP板加固混凝土梁挠度的计算方法,并与预应力CFRP板加固混凝土梁试验的挠度监测数据对比,验证其适用性。

1 预应力混凝土梁挠度计算方法

1.1 直接双线性法

直接双线性法通过将弯矩Ms分成开裂弯矩Mcr与Ms-Mcr两部分, 将预应力混凝土受弯构件在使用荷载前的挠度-弯矩曲线近似看作由两段直线组成[7]。 相应地,受弯构件的挠度f1分别由开裂前的挠度f1-1与开裂后的挠度f1-2相加获得。而按照直接双线性法的假定,f1-1和f1-2需要分别根据未开裂截面惯性矩I0与Icr计算得到。

开裂弯矩Mcr作用下

B0=0.95EcI0;

(1)

Ms-Mcr作用下

Bcr=EcIcr;

(2)

挠度计算

f1=sl2[Mcr/B0+(Ms-Mcr)/Bcr]。

(3)

式中:B0为开裂前的截面刚度;Bcr为开裂后的截面刚度;s为与荷载种类和支撑条件有关的挠度系数；l为受弯构件的计算跨度。

1.2 有效惯性矩法

有效惯性矩法是通过计算，把开裂前的截面惯性矩I0和开裂后的惯性矩Icr折算为有效惯性矩Ie, 折算比例根据开裂弯矩Mcr对使用弯矩所占比例的大小[8]。有效惯性矩与有效刚度分别为

Ie=(Mcr/M)3I0+[1-(Mcr/M)3]Icr,

(4)

Be=EcIe。

(5)

式中：M为使用弯矩。

1.3 曲率积分法

曲率积分法通过计算获得构件沿全长的曲率分布关系, 对构件曲率进行积分求得构件的挠度[7]：

f2=Sl2(1/ρ),

(6)

式中,S为与支座及荷载条件有关的变形计算系数;l为受弯构件的计算跨度; 1/ρ为曲率。

通过以上对3种方法的总结, 用直接双线法对混凝土梁挠度进行计算, 其理论依据主要来自于试验总结, 根据荷载情况把梁的受力情况分成两部分分别进行求值叠加[9]; 有效惯性矩法较为简单, 但该方法的计算仅将Mcr/M作为变量, 忽略其他因素的影响, 计算挠度值不够准确; 曲线积分法更加精确, 但由于计算繁琐不适合应用。 本文结合曲率积分法与直接双线法两种方法计算混凝土梁的挠度, 使得计算更加准确、 高效。

2 预应力 CFRP 加固钢筋混凝土梁的挠度计算方法

2.1 CFRP加固梁刚度计算

试验表明: 预应力CFRP板加固钢筋混凝土梁弯矩-曲率之间的曲线可以简化成图1所示的3个线性阶段: ①混凝土开裂前； ②混凝土开裂至受拉钢筋屈服; ③受拉钢筋屈服到极限破坏状态。 通过弯矩与曲率之间的物理关系可以得出相应的刚度。

2.1.1 钢筋屈服时梁截面应力应变分析 预应力CFRP板加固梁在屈服阶段的应力和应变分析如图2所示, 此时受拉钢筋屈服, 受压区边缘混凝土未

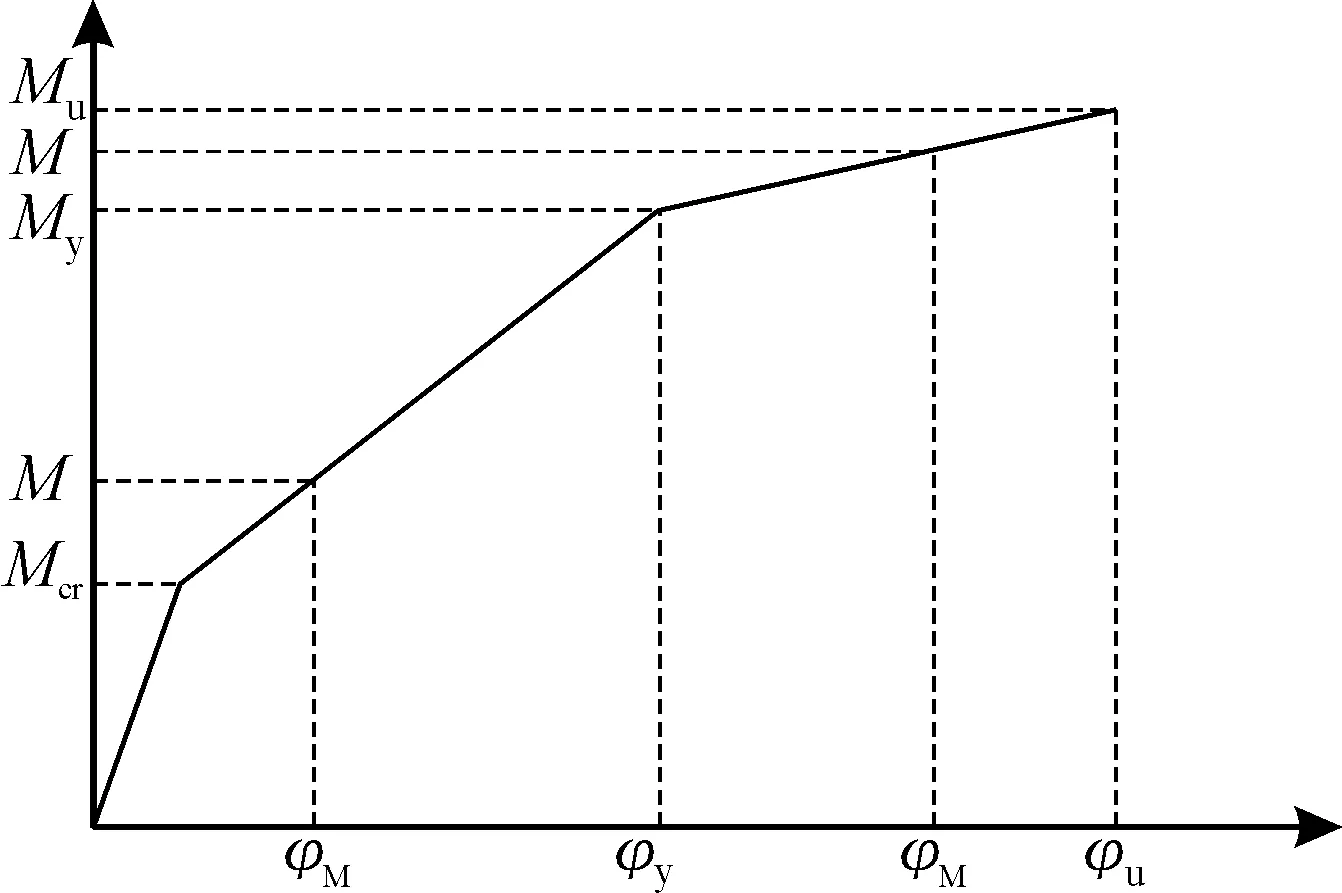
图1 弯矩-曲率关系简图Fig.1 Relationship of moment-curvature

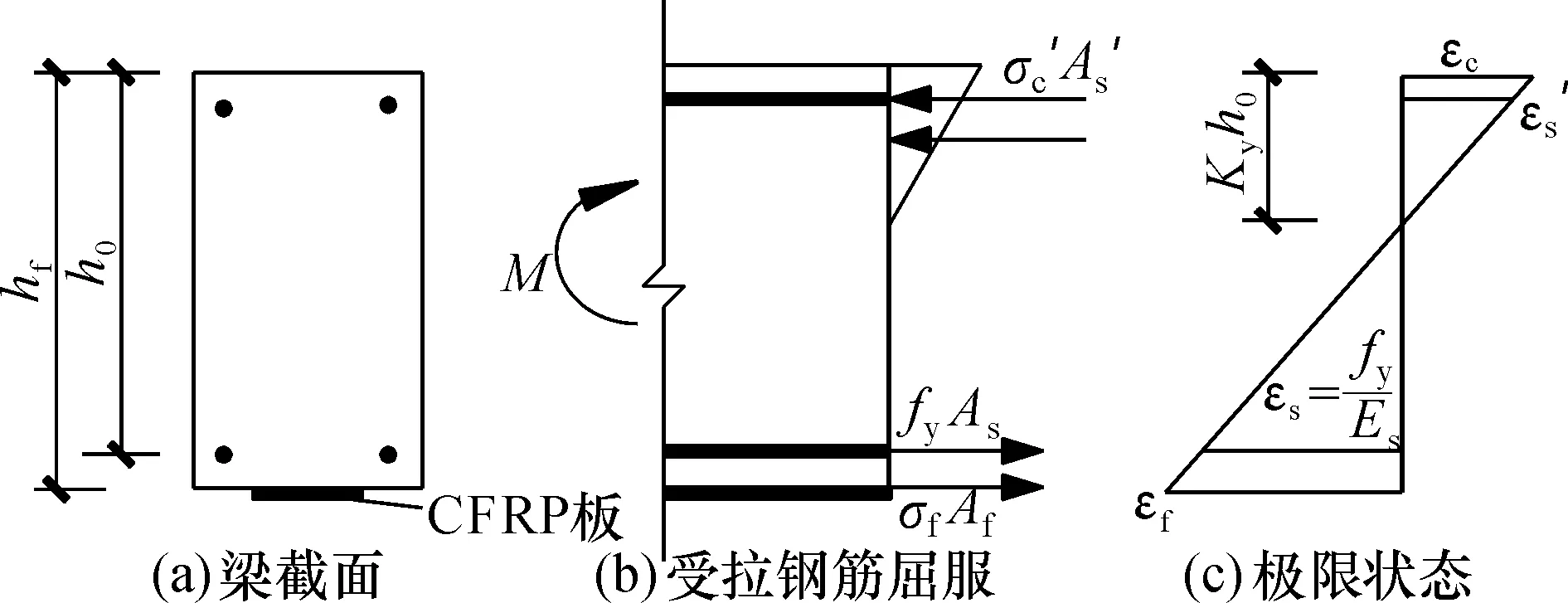
图2 屈服状态下梁截面应力及应变分布Fig.2 Stress and strain distribution of beam section under yield condition

达极限应力, 此时受压区混凝土应变分布可简化为三角形分布, 受压区钢筋未屈服, CFRP板未达极限应力。

加固后梁各部分的应变关系

(7)

式中：Ky为混凝土受压区高度系数,Ky=hf/x,γf=hf/h0。

由混凝土、 钢筋、 CFRP板应力应变关系可得

(8)

2.1.2 开裂前截面惯性矩及刚度的计算 混凝土开裂前受压区高度x0为

(ns-1)As(h0-x0)+(nf-1)Af(h-x0);

(9)

换算截面惯性矩I0为

(ns-1)As(h0-x0)2+(nf-1)Af(h-x0)2;

(10)

开裂前的截面刚度B0为

B0=0.85EcI0。

(11)

2.1.3 混凝土开裂后的截面惯性矩及刚度的计算 混凝土开裂后受压区高度xcr为

=nsAs(h0-xcr)+nfAf(h-xcr);

(12)

换算截面惯性矩Icr为

nsAs(h0-xcr)2+nfAf(h-xc)2;

(13)

根据力的平衡可以得出

(14)

将式(8)带入式(14), 求得Ky及φy的关系式

(15)

(16)

式中:ρs=As/bh0;ρs′=As′/bh0;ρf=Af/bhf;αE=Es/Ec;αEf=Ef/Ec。

屈服弯矩My

My=φyEcIcr。

(17)

对于混凝土开裂后的截面刚度计算, 可以根据弯矩曲率关系图1得到弯矩所对应的曲率, 即

(18)

则开裂后梁截面的刚度为

Bcr=M/φm。

(19)

2.2 CFRP加固梁挠度

预应力产生的挠度f1

(20)

式中：Np为CFRP板的有效预应力;ep为CFRP板有效预应力的偏心距。

荷载产生的挠度f2

f2=SMl2/Bcr,

(21)

式中：S为与荷载种类和支撑种类有关的挠度系数。

3 挠度计算验证

本文采用数据来源于预应力CFRP板加固RC梁变形性能试验, 梁尺寸 、配筋如图3所示。 用CFRP板对混凝土梁进行体外加固, 锚具为柳州欧维姆公司生产的CFRP板专用锚具, CFRP板与混凝土梁表面用专业碳板胶进行粘结填充, 提高加固梁与CFRP板的连接使用性能。 试验中混凝土梁挠度值监测使用位移计进行记录, 并将位移计与应变箱以1/2桥连接,保证试验梁挠度监测的准确性。 CFRP板的张拉如图4所示, 试验加载和数据采集如图5所示，试验结果见表1。

屈服状态下梁跨中挠度的计算值与试验值的比较如表2所示。通过试验值与计算值的对比发现,采用本文公式计算得到屈服状态下梁跨中挠度的计算值与试验值之间两者吻合度良好, 计算值对试验值的占比在90%左右, 标准差小于10%, 说明本文的相关计算公式适用性良好。 由于计算值相对于试验值略偏小,出于公式的实用性及安全性的考虑,建议将计算值提高10%使用。

图4 CFRP板张拉Fig.4 Tension of CFRP plate

图5 加载装置图Fig.5 Detail of loading device

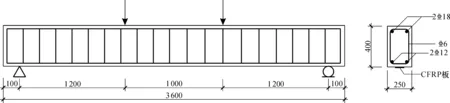
图3 梁尺寸与截面配筋图Fig.3 Beam size and section reinforcement

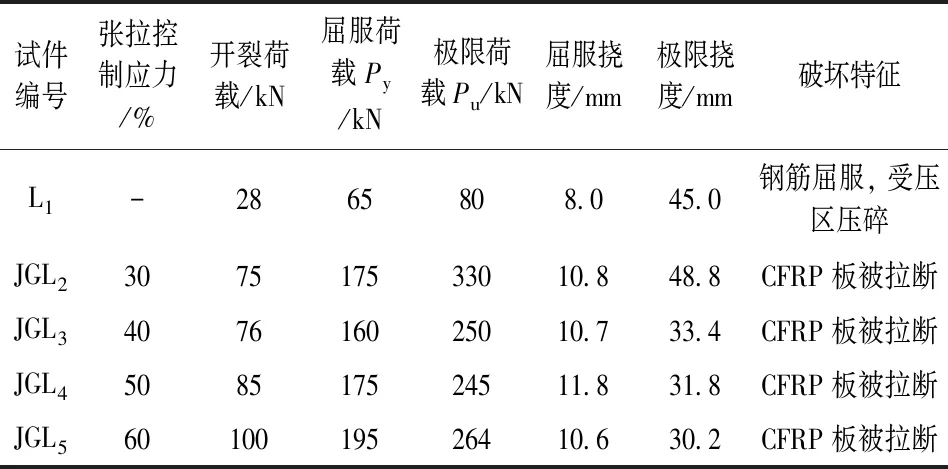
表1 试验结果

表2 屈服状态下梁跨中挠度的计算值与试验值的比较

4 结束语

通过对已有的混凝土结构挠度计算方法的分析,总结出一套基于直接双线性法和梁开裂后曲率变化的预应力CFRP板加固混凝土梁的挠度计算方法,用该方法对预应力CFRP板加固混凝土试验梁的挠度进行计算,并与监测值进行对比。结果表明,理论值与试验值的平均误差小于10%,说明本文给出的公式有很好的参考价值。

影响预应力CFRP板加固钢筋混凝土梁的变形性能有很多因素,如初始荷载水平、温度变化和收缩徐变等因素引起的预应力损失等对梁长期挠度的影响,还需作进一步的研究。