基于时间窗互相关成像条件的GPR逆时偏移成像

王敏玲,廖天元,王洪华,龚俊波,张 智,熊 彬

(桂林理工大学 a.地球科学学院;b.广西隐伏金属矿产勘查重点实验室,广西 桂林 541006)

0 引 言

偏移作为实测数据向地下真实结构转换的重要技术,是探地雷达(ground penetrating radar, GPR)高精度成像方法之一,偏移质量的优劣将直接影响后续解释的准确性[1]。目前,常用的GPR偏移方法主要有Kirchhoff偏移[2-3]、频率域波数偏移[4-5]、逆时偏移[6-7]等。众多偏移方法中,逆时偏移具有精度高、相位准确、不受横向变速和高陡倾角限制、能精确地将任意方向传播的电磁波场归位到其真实地下空间位置等优点,在GPR成像领域得到广泛关注[8]。Fisher等[9]首次将逆时偏移技术应用于GPR数据处理中;傅磊等[10]通过对比逆时偏移与Kirchhoff偏移结果，验证了逆时偏移算法的优越性；王敏玲等[11]为避免基于互相

关成像条件的逆时偏移计算中源点正传电磁波场的重建，将激发振幅成像条件应用于GPR逆时偏移成像；Bradford等[12]针对起伏地表模型的逆时偏移问题，提出了一种考虑电磁波振幅补偿的逆时偏移算法并应用于合成及实测GPR数据处理中；Lu等[13]为克服地表起伏对逆时偏移成像的影响，将基于贴体网格剖分技术应用于源点正传和接收点反传电磁波场的计算，提高了起伏地表GPR模型的成像精度；朱尉强等[14]基于时间反转不变原则，通过修改逆时传播方程，提出了一种考虑GPR衰减补偿逆时偏移方法。

上述GPR逆时偏移大都采用互相关成像条件,需要计算地下介质中每个成像点处所有时刻的源点正传电磁波场和接收点反传电磁波场的互相关。由于地下介质参数存在差异, 成像点处的源点正传电磁波场和接收点反传电磁波场中不但包含目标体的反射信号, 而且也包含介质之间相互反射和背景散射引起的杂波。 因此, 易在非反射点处产生较强的低频噪声, 降低目标体的成像质量[15]。 目前, 去除逆时偏移剖面中的杂波干扰和低频噪声方法有3种[16]:第1种是滤波[17-19],即考虑低频噪声与有效信号在波数域内的差异,利用导数滤波,Laplace滤波、空间滤波等滤波方法对噪声与有效信号进行分离,这些滤波方法在一定程度上可以去除假象,但对背景散射产生的杂波干扰的去除显得无能为力。第2种是控制方向成像[20-21],即从假象产生的原因出发,在互相关成像条件基础上,利用不同传播方向的正传和反传电磁波场进行成像,主要有坡印廷矢量法和电磁波场分解法。 当速度模型复杂时,空间上某一点的电磁波场是很多方向电磁波场的叠加,采用坡印廷矢量不能分别描述复杂结构的每个方向的电磁波场;电磁波场分解法需要对每个时刻、空间每个点进行傅里叶变换,计算量巨大。 第3种是根据偏移模型的速度信息,估计各成像点的主反射发生时间界限,并根据时间界限设计出该成像点的时间窗, 对时间窗内的正传和反传电磁波场作归一化互相关计算, 并将计算结果作为该成像点的零延迟互相关逆时偏移成像的权值系数以压制时间窗外的杂波干扰[15]。 Yang 等[22]将此方法应用于钻孔雷达的逆时偏移成像中, 数值验证该方法具有计算速度快、 压制低频噪声和杂波干扰效果好、 分辨率高等优点。

为此,本文在上述理论基础上,将时间窗互相关成像条件应用于地面GPR随机介质逆时偏移成像中。正传和反传电磁波场采用时域有限差分法(finite difference time domain method, FDTD)进行计算, 单轴各向异性完全匹配层(uniaxial perfectly matched layer, UPML)边界条件用于吸收模型截断边界处的超强反射波。时间窗内的归一化互相关成像结果作为所有时刻的归一化互相关成像结果的权值,获取逆时偏移剖面。应用基于时间窗互相关成像条件的GPR逆时偏移算法对典型GPR模型的多偏移距数据和实测数据进行逆时偏移成像,并与归一化互相关成像条件的逆时偏移结果进行对比,分析了基于时间窗互相关成像条件的GPR逆时偏移算法在压制低频噪声、去除杂波干扰和提高成像精度方面的优越性。

1 GPR逆时偏移成像原理

GPR逆时偏移的基本原理是将地表记录到的接收点电磁波场在时间轴上进行逆向传播,当电磁波场逆推至零时刻,则所有反射波与绕射波的能量都回到最初被反射和绕射的空间位置,然后应用成像条件可获取最终的偏移成像剖面[11]。因此,逆时偏移的实现过程主要分为3步:1)源点正传电磁波场的计算;2)接收点反传电磁波场的计算;3)成像条件的应用。其中,前两步可利用相同的数值模拟方法进行计算,本文采用基于UPML边界条件的FDTD来实现源点正传电磁波场和接收点反传电磁波场的计算。

成像条件的应用是开展高效高精度GPR逆时偏移的关键,它的好坏将直接影响成像质量。目前GPR逆时偏移中应用最广泛的成像条件是Clearbout等[23]提出的零延时互相关成像条件,其基本原理是根据成像点的入射波与反射波到时相同的原理,通过计算源点正传电磁波场和接收点反传电磁波场的零延时互相关,从而获得成像剖面。标准的零延迟互相关成像条件公式为

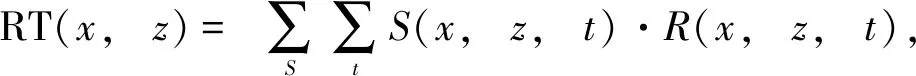
(1)

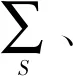
零延迟互相关成像条件具有理论简单、实现简易、计算量小等优点,但其最主要不足在于直达波和背景散射波的互相关会产生很强的低频噪声,尤其在偏移速度模型中存在相对介电常数比较明显的分界面时,这种噪声会严重干扰浅地表结构的描述,使得成像结果模糊不可辨认,且深部结构的成像能量非常微弱。

鉴于互相关成像条件的不足,Schleicher等[24]在互相关成像条件的基础上,提出了归一化互相关成像条件,其表达式为

(2)

(3)

由式(2)、 (3)可知:归一化互相关成像条件是在互相关成像条件的基础上,用源点电磁波场或接收点电磁波场进行归一化,可对成像结果整体上起到能量调解的作用。该成像条件具有削弱源点振幅影响、提升深部结构能量等优点。

2 基于时间窗互相关成像条件的GPR逆时偏移算法

由于实际地下介质的速度存在差异,各层介质之间会产生相互反射和背景杂波干扰,利用互相关成像条件进行成像时,各成像点的正传和反传电磁波场既包含目标反射信号,也包含介质之间相互反射引起的杂波干扰[15]。这些干扰信号的互相关会降低目标体的成像质量。因此,可根据偏移速度模型估计每个成像点的主反射信号产生时间,设计合理的时间窗以压制时间窗外的杂波干扰[22]。对于偏移速度模型中的某一个成像点(x,z), GPR信号主反射发生时间tk(x,z)可表示为

tk(x,z)=tmax-d(x,z)/vk,

(4)

其中:d(x,z)为成像点(x,z)到发射天线的距离;vk为电磁波在地下第k种介质中的传播速度(k=1, 2, …,K);tmax为时窗长度。 假设整个探测空间被第k种均匀介质填充, 则成像点(x,z)处产生的主反射时间可估计为d(x,z)/vk。 由于电磁波在实际介质中的传播速度在[min(vk) max(vk)]区内波动,故成像点(x,z)处的主反射产生时间介于[min(d(x,z)/vk) max(d(x,z)/vk)]。

min(d(x,z)/vk)≤tk(x,z)≤max(d(x,z)/vk)。

(5)

为压制该成像点附近处的杂波干扰,该点的时间窗上、下界限可定义为

tm1(x,z)=max(min(tk(x,z)-tw),0),

(6)

tm2(x,z)=min(max(tk(x,z)),tmax)。

(7)

其中：tw为GPR发射信号的脉冲宽度,k=1, 2, …,K。 在时间窗[tm1tm2]内, 该成像点的正传和反传电磁波场归一化互相关计算公式可表示为

(8)

其中, TG(x,z)将作为成像点(x,z)处反射强度的加权系数以抑制时间窗外的杂波干扰。因此,成像点(x,z)处的最终逆时偏移结果可表示为

NRTTG(x,z)=NRT(x,z)·TG(x,z),

(9)

其中，NRT(x,z)表示该成像点处的归一化互相关成像结果。 由式(9)可知,基于时间窗函数的GPR逆时偏移算法主要包括逆时偏移的实现和权值系数TG(x,z)的计算。 对于逆时偏移的实现过程: 首先, 利用钻孔取样、 层析成像、 全波形反演等技术获取实际地下介质的电磁波速度参数, 建立逆时偏移所需的速度模型； 然后,计算正传电磁波场S(x,z,t)和反传电磁波场R(x,z,t)； 最后，应用归一化互相关成像条件获取逆时偏移结果。

对于权值系数TG(x,z)的计算过程：根据式(6)、 (7)计算偏移速度模型各成像点的主反射时间及时间窗上、 下界限。利用式(8)求解每个成像点处的权值系数。 图1展示了某成像点处正传和反传电磁波形, 正传电磁波形到达目标的时刻为目标的主反射信号发射时刻,tmax为雷达的最大采样时间。 在获得归一化互相关成像条件的GPR逆时偏移结果和权值系数之后, 利用式(9),计算基于时间窗互相关成像条件的GPR逆时偏移剖面。

基于时间窗互相关成像条件的GPR逆时偏移成像流程如图2所示,其中内虚线框中为逆时偏移所需步骤,外虚线框中为基于时间窗函数的GPR逆时偏移所需步骤[22]。

图1 逆时偏移算法中某成像点处入射信号和反向信号传播示意图Fig.1 Timing of transmitted and reflected signals in RTM of GPR

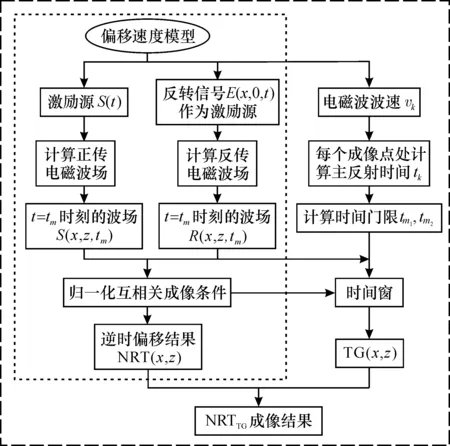
图2 基于时间窗互相关成像条件的GPR逆时偏移成像流程图Fig.2 GPR reverse time migration imaging flow chart based on time window cross-correlation imaging condition

3 数值算例

3.1 模型1

模型1是大小为1.8 m×1.0 m的圆形空洞模型, 如图3所示。 背景介质设置为干土壤,其相对介电常数为5, 电导率为0.001 S/m; 土壤中埋有一个半径为0.1 m的圆形空洞, 其圆心位置为(0.9 m, 0.5 m)。 采用二维FDTD正演算法计算正传与反传电磁波场, 计算区域被剖分成360×200的正方形网格单元, 网格间距为0.005 m×0.005 m; 模型外施加完全匹配层, 厚度为0.1 m。 采用共源观测方式, 发射源信号采用中心频率为500 MHz的雷克子波, 采样时间间隔0.01 ns, 时窗长度16 ns。 地表布设5个发射源(三角形表示), 发射源的间距为0.2 m; 第1个发射源放置在水平距离0.5 m处; 每个发射源两侧各布置50个接收源,接收点的间距为0.01 m,水平方向上覆盖了0.5 m。

图4为(0.55 m, 0.4 m)处的源点正传电磁波和接收点反传电磁波波形对比, 两条竖直虚线分别表示时间窗上、 下界限。 时间窗[4.12 ns 8.34 ns]内的正传电磁波波形与反传电磁波波形具有很强的相关性,在此时间窗内进行互相关计算,可以压制其他时刻的正传和反传电磁波场互相关运算产生的噪声干扰。

分别利用基于时间窗互相关成像条件和归一化互相关成像条件在第3个发射源点的偏移孔径内进行偏移成像获得的成像剖面如图5所示。 逆时偏移剖面中的圆形空洞均清晰可见, 验证了本文编制的基于归一化互相关成像条件和时间窗互相关成像条件的GPR逆时偏移算法的正确性和有效性。 对比图5a、 c 可知, 拉普拉斯滤波前的归一化互相关成像结果在空洞附近出现较强的背景噪声, 且地表附近受发射源强振幅影响范围更大; 而时间窗互相关成像条件的逆时偏移剖面中, 由于采用时间窗内的归一化互相关运算结果作为权值系数, 压制了目标体附近的噪声和发射源强振幅对空洞目标体的影响。 图5b、 d 为利用拉普拉斯滤波方法对图5a、 c进行滤波后获得的成像剖面。 对比滤波前后的逆时偏移剖面可知, 滤波可压制低频噪声和发射源强振幅的影响, 提高目标体的成像精度。 对比图5b、d 可知, 滤波后的时间窗互相关成像条件的GPR逆时偏移剖面的分辨率更高。

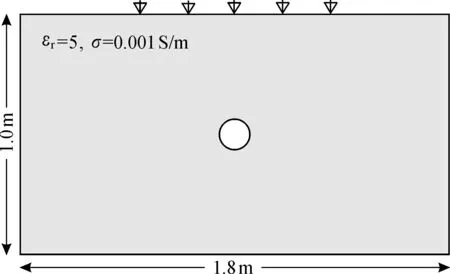
图3 圆形空洞模型示意图Fig.3 Schematic map of the circle void model

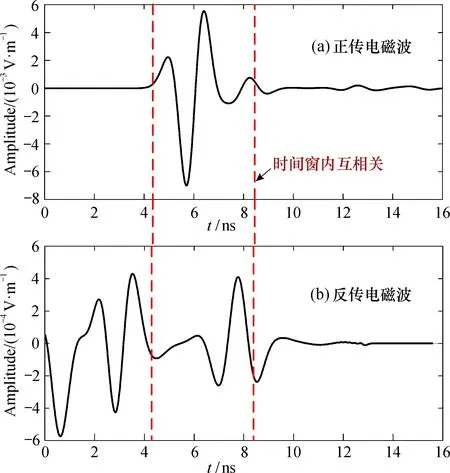
图4 x=0.55 m, y=0.4 m处的源点正传电磁波(a)与接收点反传电磁波(b)波形Fig.4 Forward and reverses electromagnetic wave forms at position of x=0.55 m, y=0.4 m

为更好地说明时间窗互相关成像条件的优越性, 分别提取图5中地表正中心位置处的单道波形能量进行对比, 图6a、 b分别为拉普拉斯滤波前、 滤波后的归一化互相关成像条件和时间窗互相关成像条件的GPR逆时偏移波形对比。 虽然时间窗互相关成像条件的逆时偏移结果中波形能量更弱些, 但波形的持续长度更小, 分辨率和精度更高。

图7为5个发射源点的逆时偏移叠加成像剖面，圆状空洞在逆时偏移剖面都清晰可见,且与空洞的真实位置相符。对比图7a、c可知,基于时间窗互相关成像条件的GPR逆时偏移算法在一定程度上压制了空洞附近的噪声,偏移剖面的低频噪声更弱。从对比滤波前后的逆时偏移剖面(图7b、d)可知,滤波后的时间窗互相关成像条件的GPR逆时偏移剖面中的空洞目标体成像结果更接近真实情况,精度更好,分辨率更高。

图5 模型1中第3个发射源的GPR逆时偏移剖面Fig.5 RTM profiles of Model 1 in the migration aperture of the 3th transmitting source with normalized cross correlation imaging condition and time gating cross correlation imaging conditiona—归一化互相关成像条件; b—归一化互相关成像条件+滤波; c—时间窗互相关成像条件; d—时间窗互相关成像条件+滤波

图6 图5中正中心位置(x=0.9 m, y=0.0 m)的单道波形能量对比Fig.6 Comparison of single waveform at center position of x=0.9 m, y=0.0 m in Fig.5

图7 GPR模型1的逆时偏移成像剖面Fig.7 RTM profiles of GPR Model 1 with normalized cross correlation imaging condition and time gating cross correlation imaging conditiona—归一化互相关成像条件;b—归一化互相关成像条件+滤波;c—时间窗互相关成像条件;d—时间窗互相关成像条件+滤波

3.2 模型2

为更好地分析时间窗互相关成像条件在背景为随机介质中的目标体的成像效果,分别建立三圆非随机介质和随机介质GPR模型,如图8所示。模型大小为2.0 m×1.0 m,分上、下两层介质,上层介质与模型1相同,埋深为0.4 m;下层介质为湿沙层,其相对介电常数为10,电导率为0.002 S/m,湿沙层中埋有3个半径为0.06 m的圆形空洞,其圆心位置(图8a)分别为(0.5m, 0.7m)、 (1.0m, 0.8m)、 (1.5m, 0.9m) 。在图 8a基础上,利用随机过程中的谱分析和椭圆自相关函数理论,建立了相应的随机介质模型, 上、 下层介质的扰动分别是0.3和0.5, 如图 8b所示。 利用二维FDTD正演算法计算电磁波在该模型中的正向及逆向传播, 计算区域被剖分成400×200的正方形网格单元, 网格间距为0.005 m×0.005 m, 模型外完全匹配层厚度为0.1 m。 采用共源观测方式,发射源信号采用中心频率为500 MHz的雷克子波, 采样时间间隔为0.01 ns, 时窗长度为20 ns。 在地表布设20个发射源,发射源的间距为0.1 m;第1个反射源放置在水平距离0 m处;每个发射源布置50个接收源,接收点间距为0.01 m,水平方向上覆盖了0.5 m。

图8 GPR模型2示意图Fig.8 Diagrams of GPR Model 2a—非随机介质;b—随机介质

图9为非随机介质模型2的逆时偏移剖面图,土壤与湿沙的分界面及3个空洞的成像清晰可见,且与真实空间位置相符。相比于滤波前的逆时偏移剖面,滤波后成像剖面的水平分界面和空洞更清晰,发射源强振幅的影响得到压制,剖面分辨率更高。对比图8b、d可知,基于时间窗互相关成像条件的GPR逆时偏移,由于采用时间窗内的归一化互相关结果作为权值系数,压制了分界面和3个空洞附近的杂波和低频噪声,偏移剖面中的低频噪声更微弱,分辨率更高。

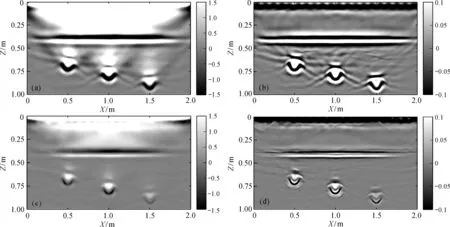
图9 非随机介质模型2的GPR逆时偏移成像剖面Fig.9 RTM profiles for nonrandom medium of Model 2 with normalized cross correlation and time gating cross correlation imaging conditiona—归一化互相关成像条件;b—归一化互相关成像条件+滤波;c—时间窗互相关成像条件;d—时间窗互相关成像条件+滤波

图10是分别利用归一化互相关成像条件和时间窗互相关成像条件对随机介质模型2进行逆时偏移, 获得的成像剖面。 可见, 土壤和湿沙的分界面和3个空洞的依然清晰可见, 但由于背景介质分布的随机性, 水平界面成像有微小扰动, 空洞异常体的形状出现扭曲现象。基于归一化互相关成像条件的逆时偏移结果中背景噪声非常强烈, 对空洞成像造成了严重干扰(图10a); 基于时间窗互相关成像条件的逆时偏移剖面中大部分背景噪声得到压制,成像精度和分辨率得到极大提高(图10d)。

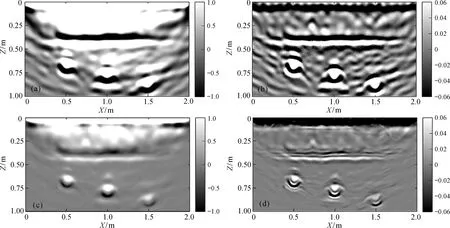
图10 随机介质模型2的GPR逆时偏移成像剖面Fig.10 RTM profiles for random medium of Model 2 with normalized cross correlation and time gating cross correlation imaging conditiona—归一化互相关成像条件; b—归一化互相关成像条件+滤波; c—时间窗互相关成像条件; d—时间窗互相关成像条件+滤波

4 实测数据的应用

为验证基于时间窗互相关成像条件的逆时偏移算法应用于实测GPR数据处理中的效果,开展地下管线GPR探测实验, 获得实测原始GPR剖面如图11a所示: 原始剖面中管线产生的双曲线反射波能量微弱, 难以识别及提取。 利用零时校正、 带通滤波、 时变增益等常规处理方法进行处理后,获得的剖面如图11b所示: 经过常规处理后的雷达剖面, 双曲线反射波更清晰, 能量更强, 噪声更低。为后续逆时偏移处理提供了高质量的GPR数据。分别利用归一化互相关成像条件和时间窗互相关成像条件对图11b所示的雷达剖面进行处理,获得的成像剖面见图11c、d:经过逆时偏移后的双曲线反射波能量收敛,反射波归位,能精确确定管线的埋深约为1.0 m,水平位置约为5.5 m。对比两图可知:相比于图11c,图11d中基于时间窗互相关成像条件的逆时偏移剖面的干扰波得到压制,成像精度和分辨率得到极大提高。

图11 实测数据的GPR剖面及其逆时偏移成像剖面Fig.11 GPR profiles and RTM profiles of observed dataa—原始GPR剖面; b—常规处理后的GPR剖面; c—归一化互相关成像条件的逆时偏移剖面; d—时间窗互相关成像条件的逆时偏移剖面

5 结 论

从逆时偏移原理出发,根据偏移模型的速度分布估算每个成像点的反射时间,设计了一个时间窗函数以压制时间窗外的杂波干扰,提出了一种基于时间窗互相关成像条件的GPR逆时偏移算法。两个典型GPR模型和实测数据的逆时偏移成像结果表明:相比于归一化互相关成像条件的逆时偏移结果,基于时间窗互相关成像条件具有能明显压制背景低频噪声的优点,成像精度更好,空间分辨率更高。