颗粒级配与孔隙比对粗粒土渗透系数的影响

丁 瑜，饶云康，倪 强，许文年，刘大翔，张 恒

(1.三峡大学三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.防灾减灾湖北省重点实验室(三峡大学)，湖北 宜昌 443002；3.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002；4.嘉兴市规划设计研究院有限公司，浙江 嘉兴 314050)

根据规范[1]，粗粒组(粒径在0.075～60 mm之间)质量大于50%的土即为粗粒类土，简称粗粒土。粗粒土作为建筑材料、基础填料以及渗滤填料在水电、建筑、道路、市政等众多工程领域广泛应用，其力学特性、渗透特性是地质工程、岩土工程领域热切关注和研究的内容[2-3]。实际工程中，粗粒土涵盖的范围十分广泛，粒径尺寸差异巨大，加之压实状态变化，其渗透性能呈现明显差异。如何准确预测粗粒土的渗透系数，评价不同级配、孔隙比对渗透系数的影响，对于相关工程的渗透分析、防渗设计具有重要意义。

渗透系数是表征土体渗透性能的宏观参数，受诸多因素影响，其中，颗粒级配和孔隙比是最主要的两个因素[4-6]。众多学者们围绕颗粒级配、孔隙比开展了大量试验研究[7-10]。基于试验成果总结，学者们提出了一些用于估算粗粒土渗透系数的经验公式[11-12]。经验公式变量主要为某些表征颗粒级配的指标，有些也包括孔隙率或孔隙比。采用经验公式估算粗粒土渗透系数，不同公式的计算结果差异较大，往往与实测结果不符[13-14]。由于试验数据有限和未能充分考虑各个粒径颗粒含量和孔隙比的影响，经验公式适用范围有限。

还有一些学者采用人工神经网络方法预测渗透系数。唐晓松等[15]采用BP神经网络，由颗粒级配预测了粗粒土渗透系数。王双等[16]以d10～dmax表征全级配，采用BP神经网络由全级配预测碎石土渗透系数，研究结果指出，级配不是反映渗透系数唯一决定的表征，但该文未考虑孔隙比的影响。而要合理地预测粗粒土渗透系数必须充分考虑各个粒径颗粒含量和孔隙比的影响。

BP神经网络因初始权值和阈值设置不合理，存在收敛速度慢、陷入局部最优等问题。为克服上述不足，可利用遗传算法对网络的初始权值和阈值进行优化，在较大范围进行搜索，代替一般的随机选取，然后应用BP网络算法对其进行精调，搜索出最优解或近似最优解。为此，本文搜集相关文献选取93组粗粒土试验数据，考虑粒径累计曲线中的d10～d100和孔隙比，采用GA-BP神经网络分析和预测粗粒土渗透系数，通过平均影响值法和试验验证，评价和探讨各级配粒径、孔隙比对渗透系数的影响。

1 样本选取与数据处理

1.1 样本选取

粗粒土渗透系数受诸多因素影响，如颗粒粒径、相对含量、密实程度、颗粒形状等。其中，颗粒级配反映颗粒粒径、相对含量；孔隙比直接与土体密实程度密切相关，也与颗粒形状有关。为此，本文以颗粒级配、孔隙比为主要因子选取样本，对粗粒土渗透系数进行预测。

由文献[7]、[8]、[11]、[17]～[20]中收集整理得到93组粗粒土渗透试验样本。其中，渗透系数为基于达西定律采用常水头试验测得的饱和渗透系数。渗透系数都是标准温度(20℃)下的渗透系数k20，避免了温度不同的影响。除渗透系数外，各样本还包括颗粒级配、孔隙比参数。

选取的样本渗透系数数量级主要为10-3～10-1cm/s，少量为10-4cm/s，为典型的粗粒土渗透系数范围。粒径范围为5～100 mm，既有大粒径也有小粒径的粗粒土。样本的孔隙比最大为0.712，最小为0.093。样本的渗透系数、颗粒粒径、孔隙比涵盖范围广，具有代表性。

1.2 数据处理

对于93组数据，采取如下数据处理方式：

孔隙比：文献[7]、[17]、[19]中直接给出了孔隙比，则直接采用；文献[8]、[18]、[20]]没有直接给出孔隙比，而给出了孔隙率，则由孔隙率换算得到；文献[11]没有直接给出孔隙比，由干密度和土粒密度换算得到。

颗粒级配：考虑了以往研究很少关注的粒径d100，以d10,d20,…,d100表征颗粒全级配。首先，根据样本数据利用Excel绘制粒径累计曲线；然后，由粒径累计曲线获取全级配d10～d100粒径。为避免手工操作误差，利用图表数字化工具(Get Data Graph Digitizer)从粒径累计曲线中准确获取粒径。经整理得到93组试验数据如表1所示。

表1 粗粒土渗透试验数据

续表1

2 GA-BP神经网络预测模型

2.1 GA-BP神经网络构建

本文网络训练函数采用trainlm函数，trainlm函数使用L-M(Levenberg-Marquardt)算法，学习速率基值为0.001、学习速率减少率为0.1、学习速率增加率为10、最大学习速率为1e10。

GA-BP神经网络模型通过Matlab软件编程实现，遗传算法采用gaot工具箱，基本步骤如下：

(1)数据归一化，划分样本。导入93组样本数据，将样本数据归一化到[-1,1]，随机选择6组样本作为检测样本，剩余87组作为训练样本。

(2)建立BP神经网络。网络采用三层结构，输入层有11个神经元，分别代表d10,d20,…,d100和孔隙比；输出层神经元为渗透系数；隐含层有12个神经元；隐含层传递函数为tansig函数，输出层传递函数为purelin函数，网络性能函数采用均方误差mse函数；最大迭代次数为1 000次，目标误差值为5e-6，最低性能梯度为1e-10。

(3)产生初始种群。编码方式采用浮点数编码，个体由输入层与隐含层、隐含层与输出层神经元之间的连接权值、隐含层和输出层的阈值四部分组成，BP神经网络为11-12-1结构，因此个体编码长度为11×12+12×1+12+1=157。个体中的变量范围为[-3,3]，种群规模为50。

(4)解码，计算适应度。解码个体得到BP神经网络的初始权值和阈值，采用训练样本的网络计算值与试验值的均方误差作为目标函数值，将目标函数值的倒数作为适应度，适应度越高，均方误差越小，则该个体越优良。

(5)选择、交叉、变异，产生新种群。选择操作采用轮盘赌法选择算子；交叉操作采用算术交叉算子，即2个个体经过线性组合产生2个新的个体；变异操作采用非均匀变异算子。

(6)重复步骤(4)和(5)，直至达到最大遗传代数100。种群适应度进化曲线如图1所示，进化75代后种群的最大适应度保持不变，平均适应度与最大适应度基本重合，此时得到最优个体。

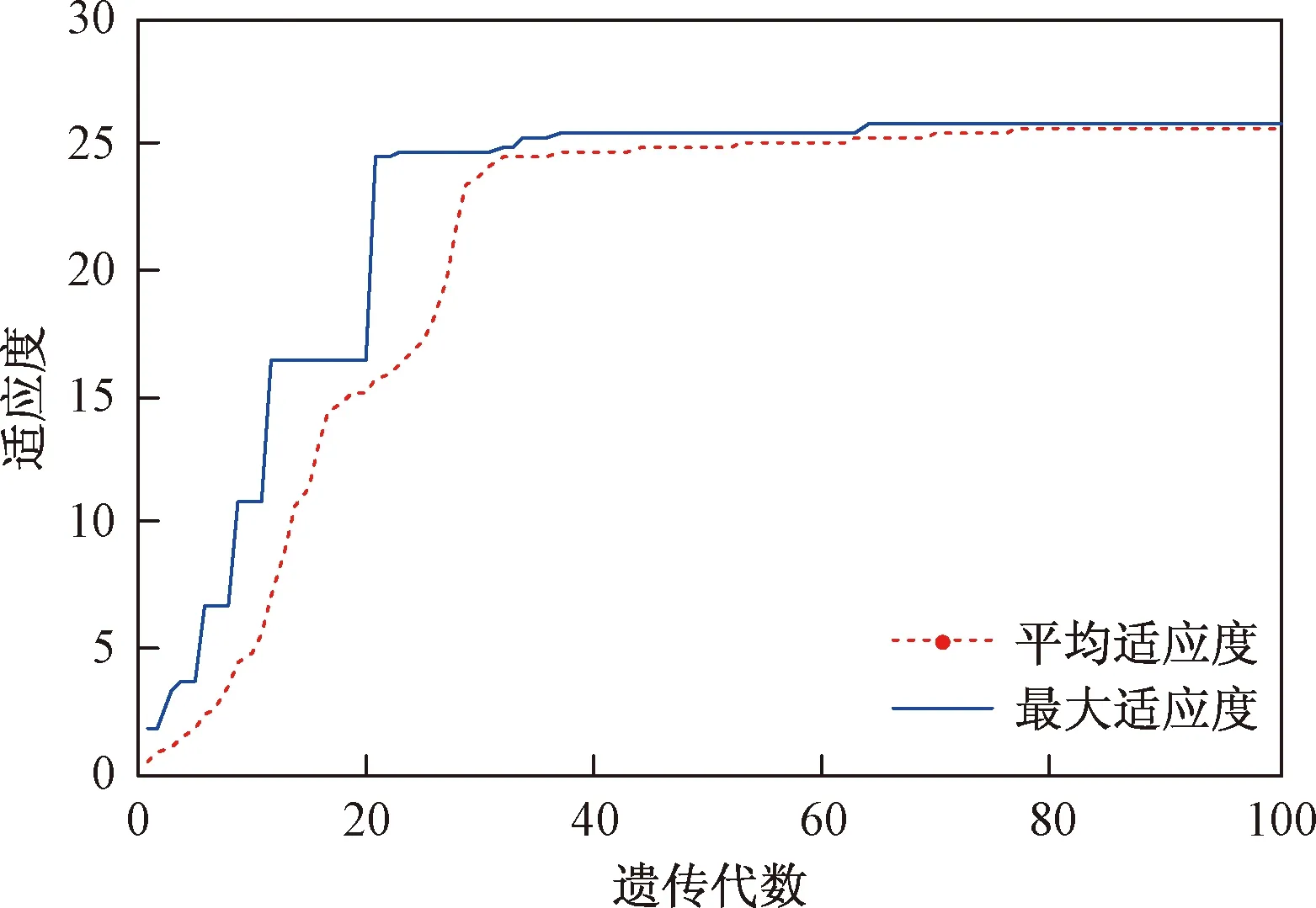
图1 适应度进化曲线Fig.1 Fitness evolution curve

(7)解码最优个体得到优化的初始权值和阈值，利用训练样本训练神经网络，通过检测样本来检验网络模型的泛化性能。

2.2 平均影响值法

平均影响值[21](mean impact value，MIV)是用于评价输入神经元对输出神经元敏感度的一个指标，其符号代表相关的方向，绝对值大小代表影响的相对重要性。采用MIV法分析d10～d100对粗粒土渗透系数的影响，具体过程如下：

(1)将1号样本中的自变量特征d10在其原值的基础上分别加和减10%，其他自变量特征保持不变，构成两个新的样本P1和P1’。

(2)将P1和P1’作为预测样本，利用建立的神经网络模型进行预测，得到两个预测结果A1和A1’，由A1减去A1’，得到1号样本关于d10的IV值。

(3)由87个训练样本分别计算，得到各样本关于d10的IV值，将87个IV值取平均值即为d10的MIV值。

(4)重复上述步骤，可得到各粒径及孔隙比的MIV值。

3 孔隙比影响验证试验

为进一步验证孔隙比对渗透系数的影响，验证网络模型的可靠性及泛化性能，确定10组粗粒土进行渗透试验。渗透试验试样包括2种级配，每一级配各5种孔隙比大小。

选取的粗粒土试样粒径范围0.1 ～10.0 mm，2种级配通过改变不同粒组含量而获得，5种不同孔隙比则通过不同击实程度来实现。试样渗透系数采用常水头渗透试验测得，试验仪器为南京土壤仪器厂有限公司TST-70型渗透仪。每组试样颗粒级配、孔隙比如表2所示。渗透试验每组试样3次平行试验，取平均值并乘以温度校正系数，求出每组试验20 ℃时的渗透系数。

表2 试样级配与孔隙比

4 结果分析与讨论

4.1 模型分析

神经网络预测精度的评价指标主要为相对误差和平均相对误差MRE，即

(1)

式中：n——样本数；

当网络经55次迭代之后达到目标误差值5e-6的要求时，停止训练。用建立的GA-BP神经网络模型预测训练样本(图2)，平均相对误差MRE为5.10%，其中有75%的样本相对误差小于平均相对误差，渗透系数预测值与试验值十分接近，相对误差在可接受范围，精度较高。

为了检验预测模型的泛化能力，用建立的网络模型对6组检测样本进行预测。6组检测样本来源于5篇文献，孔隙比最大为0.548，最小为0.121。检测样本粒径为60 ～5 mm，且渗透系数试验值数量级为10-3～10-1cm/s，为典型的粗粒土渗透系数范围。检测样本的模型预测结果与试验结果如图2和表3所示，最大相对误差为10.44%，平均相对误差MRE为6.39%，渗透系数预测值与试验值十分接近，相对误差在可接受范围，表明该神经网络的泛化性能良好。

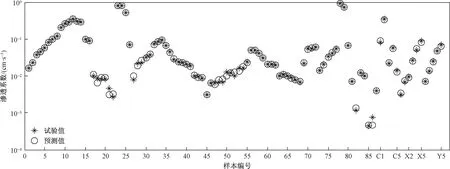
图2 训练、检测及验证试验样本的预测结果Fig.2 Predicted results of the training, testing and verification test samples

表3 检测样本的预测结果

GA-BP神经网络模型得到的预测值较好地贴合了试验值，且具有较好的泛化性能，说明颗粒级配和孔隙比是粗粒土渗透系数的主要影响因素，该神经网络能充分反映颗粒级配和孔隙比对粗粒土渗透系数的影响，采用GA-BP神经网络，由全级配能较好地预测粗粒土渗透系数。

4.2 颗粒级配对渗透系数的影响

根据神经网络模型计算结果，d10～d100的MIV值如表4所示。粒径的MIV值为正，表示该粒径增大，渗透系数增大；MIV值为负，则表示该粒径增大，渗透系数减小。各粒径MIV绝对值代表了相应粒径对渗透系数影响的相对重要性。

将各粒径的MIV绝对值除以d20的MIV绝对值(绝对值最大)得到各粒径的相对权重，如表4所示。由各粒径的相对权重可知，每一粒径对渗透系数均有直接影响，但影响程度不同。根据10个粒径的相对权重，可将其划分为高、中、低3种粒径敏感度(表4)。d20对粗粒土渗透系数影响最大，这与Terzaghi[22]、刘杰[12]、王俊杰[10]等研究结论一致，同时粒径d80和d40的影响与之相当，这3个粒径可视为影响渗透系数的关键粒径，属于高敏感度粒径；d10、d50、d100、d70的相对权重在0.5～0.7，为中敏感度粒径；其余3个粒径相对权重在0.5以下，为低敏感度粒径。

表4 各特征粒径的MIV值

d50及以下粒径的MIV值为正，d50以上粒径的MIV值为负；若其他粒径不变，增大d50及以下粒径，渗透系数就增大，而增大d50以上粒径，渗透系数则会减小。由此判断，d50是粗粒土的界限粒径。d50以上粒径的“粗颗粒”骨架作用和d50及以下粒径的“细颗粒”填充效应共同影响着粗粒土渗透系数。增大起填充作用的“细颗粒”粒径，渗流孔隙通道会增大，渗透系数就会增大；增大起骨架作用的“粗颗粒”粒径，大块骨架较多，有效渗水面积会减小，渗透系数就会减小。另外，增大d50及以下粒径，减小d50以上粒径，不均匀系数Cu=d60/d10将会减小，粗粒土级配会变得更均匀，渗透系数将会有所增大。

对比可知，d10～d50的MIV绝对值之和是d60～d100的MIV绝对值之和的1.40倍，表明粗粒土中的“细颗粒”对渗透系数的影响较“粗颗粒”更大，同时也说明“粗颗粒”的骨架作用对粗粒土渗透系数也有重要影响。有的学者认为粗粒土渗透系数主要决定于细粒，这种观点由于忽视粗料的骨架作用是不全面的。

4.3 孔隙比对渗透系数的影响

神经网络模型计算的孔隙比MIV值为0.0401，正值表明渗透系数与孔隙比呈正相关关系。通过对比不难发现，孔隙比的MIV绝对值大于任一特征粒径。相对于各特征粒径，孔隙比是影响渗透系数更为敏感的因子。对于相同级配的粗粒土而言，孔隙比大小可以作为表征渗透系数大小的主要指标，因此，不少学者均考虑了孔隙比建立经验公式[11-12]。

对于孔隙比影响，进一步的验证试验实测结果及GA-BP网络模型预测结果如表5所示。级配X的粗粒土，孔隙比为0.65(对应压实度为80%)的实测渗透系数约为孔隙比为0.38(对应压实度为95%)的13倍；级配Y的粗粒土，孔隙比为0.67(对应的压实度为81%)的实测渗透系数约为孔隙比为0.43(对应的压实度为95%)的10倍。模型预测得到的2种级配的粗粒土渗透系数与孔隙比之间的关系如图3所示。预测与试验规律一致，精度能够满足工程要求。

表5 验证试验结果与预测结果

图3 模型预测渗透系数与孔隙比关系Fig.3 Relationships between the modeled coefficientsof permeability and void ratios

相同级配的粗粒土压实过程中，松散状态时孔隙比变化引起的渗透系数剧烈变化；达到一定密实状态后，孔隙比变化时渗透系数变化幅度逐渐减小。试验结果表明，对于相同级配的粗粒土，渗透系数与孔隙比密切相关，孔隙比变化可使渗透系数出现跨数量级变化。孔隙比对渗透系数影响显著。因此，对粗粒土渗透系数进行分析、预测时，应考虑孔隙比大小。

土体孔隙包括有效孔隙(连通孔隙)和无效孔隙(半连通、不连通孔隙)[23]，孔隙比是多孔介质孔隙大小、连通性等孔隙结构特征的宏观平均表征。土体的渗透性能主要取决于有效孔隙，分析认为，粗粒土渗透性能随孔隙比变化的规律，与不同压实状态下有效孔隙的主导作用不同有关。松散状态下，粗粒土压实时，孔隙尺寸减小、连通状态变化明显，有效孔隙起支配作用，渗透系数随孔隙比减小降低明显。达到一定密实状态后，虽然有效孔隙、无效孔隙随着压实均会进一步减小，有效孔隙的支配作用降低，无效孔隙的影响相应增加，因而渗透系数变化的趋势减弱。

粗粒土中粗颗粒的骨架作用和细颗粒的填充作用共同影响着渗透系数，各级配粒径对渗透系数的影响程度不同。粗粒土孔隙比减小，渗透系数可跨数量级降低，孔隙比对渗透系数的影响与有效孔隙变化及支配作用密切相关。因此，准确计算和评价粗粒土渗透系数，应当充分考虑颗粒级配、孔隙比。

5 结论

(1)各级配粒径对渗透系数均有直接影响，且影响程度不同，按相对权重，d20、d80、d40属于高敏感度粒径，为关键粒径，影响最大；d10、d50、d100、d70的相对权重在0.5～0.7，为中敏感度粒径；d30、d90、d60相对权重在0.5以下，为低敏感度粒径。

(2)粗粒土中粗颗粒的骨架作用、细颗粒的填充作用共同影响着渗透系数，d50为粗粒土的界限粒径，d50及以下粒径对渗透系数的影响大小为d60～d100粒径的1.4倍，即“细颗粒”对渗透系数的影响较“粗颗粒”更大。

(3)粗粒土孔隙比变化可使渗透系数产生数量级差异，孔隙比对渗透系数的影响规律与不同压实状态下有效孔隙主导作用的不同直接相关。

(4)颗粒级配和孔隙比是粗粒土渗透系数的主要影响因素，采用GA-BP神经网络，由全级配和孔隙比能较好地预测粗粒土渗透系数，可在实际工程进行应用。