用数学归纳法证明伴X基因频率在两性中相等*

张韶杰

（中山市第一中学 广东中山 528403）

人教版必修2 教材“人类遗传病”一节中有一道讨论题：“红绿色盲中男性发病率为7%，女性发病率为0.5%。你计算的发病率是否接近上述数据［1］？”很多学生认为7%和0.5%指在整个人群中XbY 和XbXb的基因型频率。实际上，与常染色体遗传病的发病率不同，伴性遗传病的发病率常指在相应性别中的发病概率，教材在此处叙述得比较模糊。根据伴性遗传平衡定律，由男性中XbY%=7%，可得该性别中Xb%=7%，则女性中XbXb%=（Xb%）2=（7%）2=0.49%，与调查得到的0.5%数据基本接近。但学生难以理解的是为何由男性得出的色盲基因频率就是人群中或女性中的基因频率。现行生物学教材中也没有出现遗传平衡定律，只是在“现代生物进化理论的主要内容”一节中以“思考与讨论”的形式呈现［1］，且没有延伸到伴性遗传中。本文通过数学归纳法推导出伴性遗传平衡定律及其相关规律，并结合相关题目说明这些规律的实际运用。

1 伴X 基因频率在两性中为什么是相等的？

理解该问题是利用伴性遗传平衡定律解决相关问题的前提，中学教师往往采用以下几种方式处理。

1.1 简单记忆法 这样做可节省时间，对一些基础差的学生也只好如此。但一些思维习惯好的学生总是想搞清楚为什么，而且不加理解的记忆并不能灵活处理各种问题。

1.2 简单理解法 以色盲为例，根据X 染色体交叉遗传的特点，因男性患者的色盲基因来自其母亲，将来又会传给其女儿，故在两性中相等。伴X 显性遗传同样如此理解，但这种解释比较牵强，仍然不能满足部分学生的刨根问底。

1.3 棋盘验证法 假设色盲基因频率在两性中是相等的（设XB=p，Xb=q）。由于基因频率可看作是相应配子的比率（注意男性可产生X 和Y 2 种比例相等的精子），随机婚配可看作精、卵的随机结合，因此，可利用棋盘格法推出随机婚配后代的各基因型频率［2］。

表1 利用棋盘格法表示随机交配过程

表1所得的各基因型频率是基于整个人群的。由于人群中男女比例为1∶1，所以在女性中：XBXB=p2，XBXb=2pq，XbXb=q2；在男性中：XBY=p，XbY=q。这正是很多中学教师给学生补充的伴性遗传平衡定律的内容，而本定律成立的前提就是伴X 基因频率在两性中是相等的。2016年全国乙卷第6 题就直接考查了定律的内容：

理论上，下列关于人类单基因遗传病的叙述，正确的是（D）。

A．常染色体隐性遗传病在男性中的发病率等于该病致病基因的基因频率

B．常染色体隐性遗传病在女性中的发病率等于该病致病基因的基因频率

C．X 染色体隐性遗传病在女性中的发病率等于该病致病基因的基因频率

D．X 染色体隐性遗传病在男性中的发病率等于该病致病基因的基因频率

为了更好地检测学生对于伴性遗传平衡定律的理解程度，笔者改编了一道相关题目：

（多选题）红绿色盲为伴X 隐性遗传病，抗维生素D 佝偻病为伴X 显性遗传病。调查某一城市人群中男性红绿色盲发病率为P、男性抗维生素D 佝偻病发病率为Q。下列叙述正确的是（B、C）。

A.女性中色盲发病率大于P

B.人群中女性抗维生素D 佝偻病发病率大于Q

C.男性中色盲基因频率为P，抗维生素D 佝偻病基因频率为Q

D.抗维生素D 佝偻病女患者的父亲和母亲可以都正常

解析：本题答案为B、C。设致病基因分别为Xb和XD，则Xb%=XbY%=P（0＜P＜1），XD%=XDY%=Q（0＜Q＜1），且在两性中是相同的，故C 正确。女性色盲的发病率XbXb%=（Xb%）2=P2＜P，故A 错误。女性抗VD佝偻病的发病率=（XD%）2+2XD%×Xd%=Q2+2Q（1-Q）=Q+Q（1-Q）＞Q，故B 正确。抗VD佝偻病为伴X 染色体显性遗传病，根据X 染色体的交叉遗传特点，女患者必有一个XD基因来自于双亲中的一位，则其双亲必有一人为患者，故D 错误。

1.4 数据计算法 设XB和Xb的基因频率在男性中分别为0.4 和0.6，在女性中分别为0.7 和0.3，利用棋盘格法得出随机婚配后代的各基因型频率［3］。

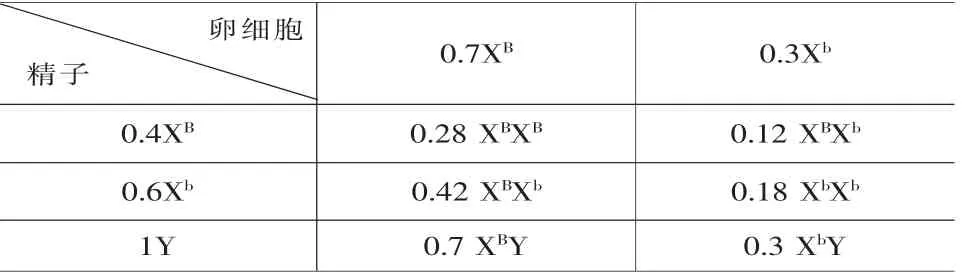
表2 利用棋盘格法表示随机交配过程

女性中XB的基因频率=（2×0.28+0.54）／2=0.28+0.54／2=0.55（即XB=XBXB+XBXb／2），同理可得Xb=0.45。

男性中XB的基因频率=0.7／1=0.7(即XB= XBY)，同理可得Xb=0.3。

如此逐代随机交配各代的基因频率，以及在两性中的差值如表3［4］。

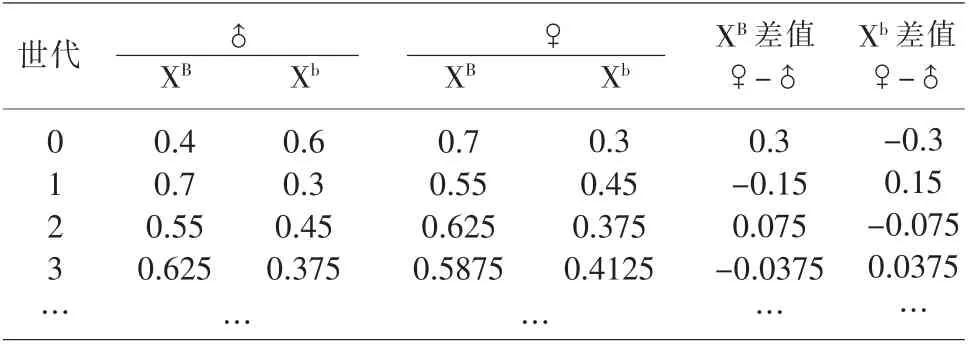
表3 逐代随机交配各代的基因频率

计算到第3 代就可发现：伴X 基因频率在两性间的差值每代减少一半。如此大部分学生可接受“色盲基因频率在两性中相等”这一事实，而且也真正理解了遗传平衡定律的适应条件：种群非常大、能自由交配、无迁入和迁出、无自然选择、无基因突变。表2和表3也显示了X 染色体交叉遗传的特点，即男性的发病率刚好是上一代女性中色盲基因频率，而男性中色盲基因频率就等于男性的发病率。

2 用数学归纳法推导伴X 基因频率在两性中差值的变化规律

设随机交配的大群体中一对伴X 基因XB和Xb，令雌性中第n 代XB和Xb的基因频率分别为Fn和fn（起始基因频率分别为F0和f0），雄性中第n 代XB和Xb的基因频率分别为Mn和mn（起始基因频率分别为M0和m0）。令M0≠F0，m0≠f0。据表3可采用归纳推理法得出Fn-Mn=（-0.5）n×（F0-M0）［5］，但假说的正确与否必须经过严谨的科学证明。

由棋盘格法得出第n+1 代各基因型频率如表4。

表4 利用棋盘格法表示随机交配过程

则第n+1 代雌性中XB的基因频率：Fn+1=，同理可得等。

第n+1 代雄性中XB的基因频率：Mn+1=XBY=Fn，同理可得Mn=Fn-1等。

所以Fn-Mn=（Fn-1+Mn-1）-Fn-1=-0.5（Fn-1-Mn-1），

而Fn-1-Mn-1=-0.5（Fn-2-Mn-2），Fn-2-Mn-2=-0.5（Fn-3-Mn-3）……

所以Fn-Mn=（-0.5）2×（Fn-2-Mn-2）=……=（-0.5）n×（F0-M0）。

以上证明采用了高中数学归纳法的思想，它属于完全严谨的演绎推理法，平时的教学中可引导有兴趣的学生进行证明。教学中利用好这些学科间的交叉联系，可有效训练学生的理性思维，提升学生的生物学核心素养。

3 如何求出伴X 基因平衡后的基因频率？

上述证明过程表明：若随机交配逐代进行，伴X 基因频率将在两性间摆动，最后差异消失，群体趋于平衡。这与常染色体上只需一个世代的随机交配即可达到平衡不同。最终两性的基因频率会无限接近于何值？可以先简单理解：男、女的性染色体组成分别为XY 和XX，人群中男女比例为1∶1。所以可认为X 染色体有存在于女性中，有存在于男性中。最终相同时的XB基因频率应为［5］。仍以上述色盲为例，F0=0.7，M0=0.4，代入公式可得p=0.6，而Xb的基因频率q=1-p=0.4。这仅是初步猜想，证明过程如下：

由公式Fn-Mn=（-0.5）n×（F0－M0）及公式Mn+1= Fn

可得Mn+1－Mn=（-0.5）n×（F0－M0）

n=0 时，M1－M0=（-0.5）0×（F0－M0）

n=1 时，M2－M1=（-0.5）1×（F0－M0）

……

n=n-1 时，Mn－Mn-1=（-0.5）n-1×（F0－M0）

n=n 时，Mn+1－Mn=（-0.5）n×（F0－M0）

以上式子相加可得：

Mn+1－M0=（F0－M0）［（-0.5）0+（-0.5）1+（-0.5）2+……+（-0.5）n］

令n=n-1，则Mn－M0=（F0－M0）［（-0.5）0+（-0.5）1+（-0.5）2+……+（-0.5）n-1］

4 两性的伴X 基因频率在逐代随机交配时无限接近的过程

由上述证明过程同理可推出女性中第n 代XB的基因频率公式，过程如下：

由公式Fn－Mn=（-0.5）n×（F0－M0）及公式Mn+1=Fn

可得Fn－Fn-1=（-0.5）n×（F0－M0）

n=1 时，F1－F0=（-0.5）1×（F0－M0）

n=2 时，F2－F1=（-0.5）2×（F0－M0）

……

n=n-1 时，Fn-1－Fn-2=（-0.5）n-1×（F0－M0）

n=n 时，Fn－Fn-1=（-0.5）n×（F0－M0）

以上式子相加可得：

Fn－F0=（F0－M0）［（-0.5）1+（-0.5）2+……+（-0.5）n］

总结2 个公式，第n 代中XB的基因频率在男女中分别为：

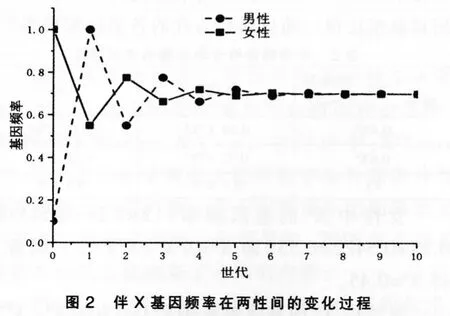
假 设M0=0.1，F0=1，则Mn=0.7－0.6（-0.5）n，Fn=0.7+0.3（-0.5）n。可利用这2 个函数，结合Excel软件中的公式输入与作图功能，形象展现逐代随机交配时伴X 基因在两性中趋于平衡的过程。具体过程如下：B2、C2 输入起始基因频率，B3 输入公式“=0.7-0.6*POWER（-0.5，A3）”，C3 输入公式“=0.7+0.3*POWER（-0.5，A3）”，然后用B、C 列所输出的基因频率画出折线图［6］。从图2中可以看出，只需经过7～8 个世代后，XB基因频率就可平衡在0.7 的水平。通过修改起始频率即可呈现各种平衡过程图表。在教学中若向学生简单展示该过程，必然能加深学生对于伴X 基因平衡过程的认识，同时也激发学生对于生物学的探索和兴趣。