样本量估计及其在nQuery和SAS软件上的实现——均数比较(九)*

南方医科大学公共卫生学院生物统计学系(510515) 王 岩 钱若远 陈平雁

1.3 多样本的均数比较

1.3.1 差异性检验

1.3.1.4 协方差分析(ANCOVA)

(1-43)

计算样本量时，先设定样本量初始值，然后迭代样本量直到所得的检验效能满足设定值为止，此时的样本量即研究所需的样本量[2]。

【例1-27】某研究欲比较三种不同教学干预方法(有声思维教学法、指导性阅读思维教学法、指导性阅读教学法)对小学四年级学生阅读理解能力的影响。采用平衡设计，在干预前后分别评估受试者的错误检测任务(error detection task，EDT)得分。以干预前EDT得分和干预后理解监控问卷(comprehension monitoring questionnaire)得分为2个协变量，干预后EDT得分为因变量进行协方差分析。根据既往研究数据，三组均值分别为8.2220，9.8148，6.1904，标准差为2.3788，ρ2为0.4434，设定检验水准为0.05，试以检验效能分别为0.8和0.9进行样本量估计。

nQuery Advanced实现:设定检验水准α=0.05；检验效能分别取80%和90%。依据上述基础数据可知，G=3，c=2，ρ2=0.4344，σ=2.3788，r1=r2=r3=1，μ={μ1,μ2,μ3}={8.2220,9.8148,6.1904}计算可得V=2.20，在nQueryAdvanced 主菜单选择：

Design：⊙Fixed Term

Goal：⊙Means

No.of Groups：⊙>Two

Analysis Method：⊙Test

方法框中选择Analysis of Covariance(ANCOVA)。

在弹出的样本量计算窗口将各参数键入，如图1-65所示，检验效能取80%的结果N=18，即总样本量为18例，每组6例。检验效能取90%的结果N=22，即总样本量为22例，三组例数分别为8例、7例和7例(因总例数不是组数的整倍数，故各组例数不绝对相等)。

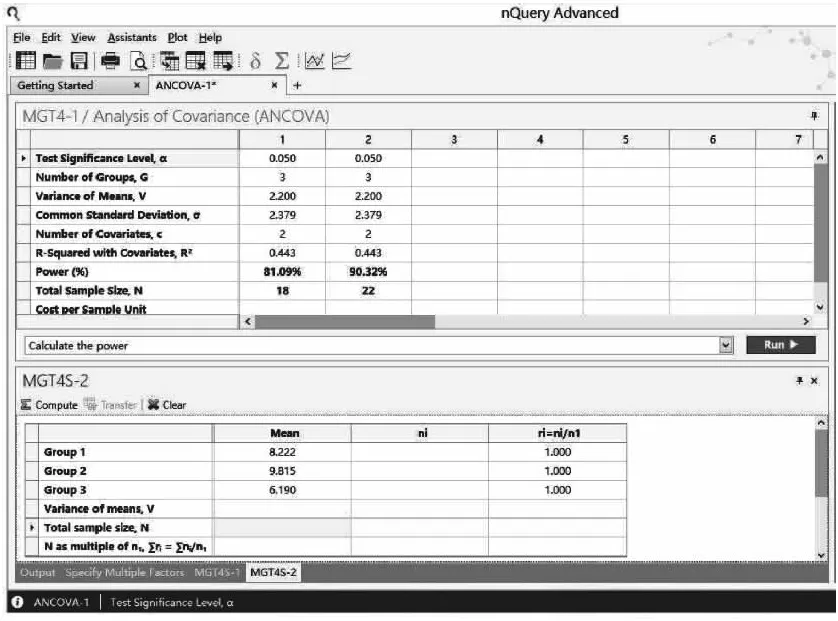
图1-65 nQuery Advanced 关于例1-27样本量估计的参数设置与计算结果

SAS 9.4软件实现：

%let u={8.2220 9.8148 6.1904}; /*各组均值*/

%let r={1 1 1}; /*各组样本量与第一组(参照组)样本量的比值*/

proc IML;

start MGT4_1(a,G,sd,c,R2,power);

error=0;

if ( a>=1 | a<=0 ) then do; error=1; print "Error" "Test significance Level must be in 0-1"; end;

if ( sd<=0 ) then do; error=1; print "Error" "Common standard deviation must be >=0"; end;

if (G<=0 | ceil(G)^=G) then do; error=1; print "Error" "The Number of groups must be positive integer "; end;

if (c<=0 | ceil(c)^=c) then do; error=1; print "Error" "The Number of coveriates must be positive integer "; end;

if(power>=100 | power<1) then do; error=1; print "error" "Power(%) must be in 1-100"; end;

if(R2>1 | R2<0) then do; error=1; print "error" "R_squared value must be in 0-1";end;

if(error=1) then stop;

if(error=0) then do;

n1=ceil(c/G+1); n=n1#&r.;sum_N=n[1,+]-0.01;

do until(pw>=power/100);

sum_n=ceil(sum_n+0.01); n1=sum_N/&r.[1,+]; n=n1#&r.;

u_mean=(n#&u.)[,+]/sum_N;

v=(&r.#(&u.-u_mean)##2)[,+]/&r.[,+];

n_mean=sum_N/G;

sigma_e2=(1-R2)*sd##2;

lamda=n_mean*G*v/sigma_e2;

df1=G-1;df2=sum_N-G-c;

f=finv(1-a,df1,df2);

pw=1-probf(f,df1,df2,lamda); pw1=100*pw;

end;

end;

print a[label="Test Significance level"]

G[label="Number of groups"]

V[label="Variance of means"]

sd[label="Common standard deviation"]

c[label="Number of coveriates"]

R2[label="R_squared value between the reponse and the covariates"]

Pw1[label="Power(%)"]

sum_N[label="Total sample size"];

finish MGT4_1;

run MGT4_1(0.05,3,2.3788,2,0.4434,80);

run MGT4_1(0.05,3,2.3788,2,0.4434,90);

quit;

SAS 9.4运行结果：

图1-66a SAS 9.4关于例1-27样本量估计的参数设置与计算结果(power=80%)

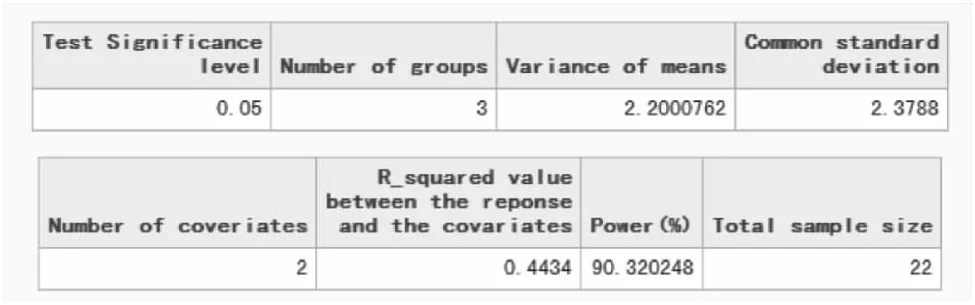
图1-66b SAS 9.4关于例1-27样本量估计的参数设置与计算结果(power=90%)

1.3.1.5 多变量方差分析(MANOVA)

方法：多变量方差分析针对分析中有多个反应变量的情况，目前有多种常用统计量可用于分析，nQuery给出了其中三种供用户选择，分别是Wilks’似然比统计量、Pillai-Bartlett Trace统计量、Hotelling-Lawley Trace统计量。Muller and Barton (1989)[3]，以及 Muller，LaVange，Ramey(1992)[4]等给出了多变量方差分析的样本量和检验效能的估计方法，各主效应及其交互效应的检验效能估计是建立在各自的自由度及非中心参数的F分布上。其检验效能的计算公式为：

1-β=1-ProbF(F1-α,df1,df2,df1,df2,λ)

(1-44)

式中，df1，df2代表F分布的自由度，λ为非中心参数，根据不同的统计量，其各参数计算方式如下：

首先，我们用p代表因变量个数，q代表所研究的分组变量的水平数，X代表设计矩阵,r代表设计矩阵的秩，M代表均值矩阵，Σ代表协方差矩阵，C代表对比矩阵，不同效应的检验可以构建不同对比矩阵C，N代表总样本量。Wilks’似然比统计量、Pillai-Bartlett Trace统计量、Hotelling-Lawley Trace统计量可基于如下矩阵构建 ：

H=(CM)′[C(X′X)-1C′]-1(CM)

(1-45)

E=Σ(N-r)

(1-46)

T=H+E

(1-47)

(1)Wilks’ Lambda

利用矩阵(1-46), (1-47)可得Wilks’似然比统计量：

W=|ET-1|

(1-48)

该检验统计量转化为近似的F统计量为：

(1-49)

其中，

df1=ap，

df2=g[(N-r)-(p-a+1)/2]-(ap-2)/2，

(2) Pillai-Bartlett Trace

利用矩阵(1-45)，(1-47)可得Pillai-Bartlett Trace统计量：

PBT=tr(HT-1)

(1-50)

该检验统计量转化为近似的F统计量为：

(1-51)

其中，

df1=ap，

df2=s[(N-r)-p+s]，

(3)Hotelling-Lawley Trace

利用矩阵(1-45), (1-46)可得Hotelling-Lawley Trace统计量：

HLT=tr(HE-1)

(1-52)

该检验统计量转化为近似的F统计量为：

(1-53)

其中，

df1=ap，

df2=s[(N-r)-p-1]+2，

对于上述各统计量，其非中心参数λ为：

λ=F·df1

(1-54)

计算样本量时，先设定样本量初始值，然后选择相应统计方法并迭代样本量直到所得的检验效能满足设定值为止，此时的样本量即研究所需的样本量[2]。

【例1-28】某研究欲比较不同教学方法在培养中学生良好学习行为中的作用，教学方法分为传统教学组、视听教学组和对照组三个组，因变量包括4个衡量学习行为的指标：学习环境、学习习惯、笔记能力和总结能力。根据既往研究，均值矩阵如矩阵M所示，协方差矩阵如矩阵Σ所示，设定检验水准为0.05，检验效能为80%，试采用Wilks’ Lambda方法据此参数进行样本量估计。

nQuery Advanced实现:设定检验水准为α= 0.05；检验效能取80%。依据上述基础数据可知，p=4，试验包含1个影响因素，其水平数为3，均值矩阵如矩阵M所示，协方差矩阵Σ如矩阵所示。在nQueryAdvanced 主菜单选择：

Design：⊙Fixed Term

Goal：⊙Means

No.of Groups：⊙>Two

Analysis Method：⊙Test

方法框中选择Multivariate Analysis of Variance(MANOVA)。

在弹出的样本量计算窗口将各参数键入，如图1-67a所示，均值矩阵和协方差矩阵如图1-67b和图1-67c所示，结果n和N分别为37和111，即每组样本量为37例，总样本量为111例。

图1-67a nQuery Advanced 关于例1-28样本量估计的参数设置与计算结果

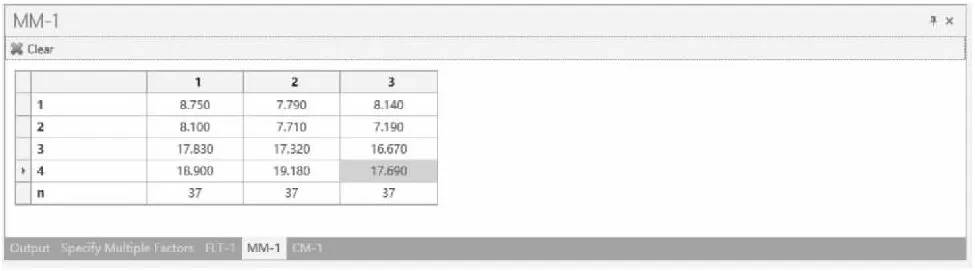
图1-67b nQuery Advanced 关于例1-28样本量估计的参数设置与计算结果(均值矩阵)

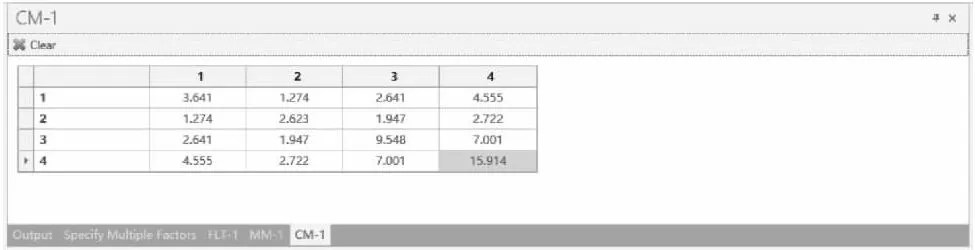
图1-67c nQueryAdvanced 关于例1-28样本量估计的参数设置与计算结果(协方差矩阵)

SAS 9.4软件实现：

%let f_level={3}; /*各分组变量的水平数*/

%let m= { 8.75 7.79 8.14,8.10 7.71 7.19,17.83 17.32 16.67,18.90 19.18 17.69};

/*因变量在所有分组变量各个水平组合下的均值*/

prociml;

start MGT3(alpha,power,p,f,rho,sd,sigma_def,method);

f_level=&f_level.;

m=t(&m.);

/*parameter check*/

error=0;

if ( alpha>=1 | alpha<=0 ) then do; error=1; print "Error" "Test significance Level must be in 0-1"; end;

/*参数f代表分组变量个数，不超过3个*/

if (f^=1 & f^=2 & f^=3) then do; error=1; print "Error""The number of factors must be in 1,2,3";end;

/*参数power代表各个效应的检验效能向量；当研究包含A和B两个分组变量时，可依次定义A、B及其交互效应AB的检验效能；当研究包含A、B、C三个分组变量时，可依次定义A、B、C、AB、AC、BC、ABC的检验效能*/

if f=1 & nrow(power)^=1 & ncol(power)^=1 then do;error=1;print "Error""Please input power of factor A";end;

if f=2 & nrow(power)^=3 & ncol(power)^=3 then do;error=1;print "Error""Please input power of factor A,factor B,factor AB (input "." if missing)";end;

if f=3 & nrow(power)^=7 & ncol(power)^=7 then do; error=1; print "Error""Please input power of factor A,factor B,factor C,factor AB,factor AC,factor BC,factor ABC (input "." if missing)"; end;

if (p<=0 | ceil(p)^=p) then do; error=1; print "Error" "The number of response variables must be a positive integer "; end;

if error=0 then do; q=1;do i=1 to f; q= q * &f_level.[i]; end;end;else stop;

if nrow(f_level)^=f then do;error=1; print "Error""The row number of factor levels should be equal to the number of factors";end;

if ncol(m)^=p then do; error=1; print "Error" "The row number of mean matrix should be equal to the number of response variables"; end;

if nrow(m)^=q then do; error=1; print "Error" "The column number of mean matrix should be equal to the product of factor levels"; end;

/*协方差矩阵可以由参数rho和sd生成，也可以由参数sigma_def直接定义*/

if (rho^=.& (rho>=1 | rho<=0)) then do; error=1;print "error" "Correlation must be in 0-1";end;

if (sd^=.& ( sd<=0 )) then do;error=1; print "Error" "Standard deviation at each level must be >=0"; end;

if (sigma_def^=.& (ncol(sigma_def)^=p | nrow(sigma_def)^=p)) then do;

error=1; print "Error" "The row and column numbers of covariance matrix should be equal to the number of response variables"; end;

/*参数method代表所选用的检验统计量，其中1=Wilks' Lambda统计量，2=Pillai-Bartlett Trace统计量，3=Hotelling-Lawley Trace统计量。*/

if (method^=1 & method^=2 & method^=3) then do; error=1; print "Error""method must be in 1,2,3";end;

if (rho^=.& sd^=.) then do;

covariance=rho*sd**2;sigma=j(p,p,covariance);

do i=1 to p; sigma[i,i]=sd**2; end;

end;

else sigma=sigma_def;

if(error=1) then stop;

if(error=0)then do;

/*C matrix*/

max_level=&f_level.[<>,];

origin_c=j(max_level-1,max_level,0);

origin_j=j(max_level-1,max_level,.);

do i=2 to max_level;

e1=-(i-1)/sqrt(i*(i-1)); e2=1/sqrt(i*(i-1)); e3=j(1,i-1,e2); e4=1/sqrt(i);

e5=j(1,i,e4);

index=max_level+1-i;

origin_c[index,index]=e1;

origin_c[index,index+1:max_level]=e3;

origin_j[index,index:max_level]=e5;

end;

f1=&f_level.[1]; index1=max_level-f1+1;

C1=origin_c[index1:max_level-1,index1:max_level];

J1=origin_j[index1,index1:max_level];C_A=C1; power_a=power[1];

if f>1 then do;

f2=&f_level.[2]; index2=max_level-f2+1; C2=origin_c[index2:max_level-1,index2:max_level];

J2=origin_j[index2,index2:max_level];

C_A=C1@J2;C_B=J1@C2;C_AB=C1@C2;

power_b=power[2];power_ab=power[3];

end;

if f>2 then do;

f3=&f_level.[3];

index3=max_level-f3+1;

C3=origin_c[index3:max_level-1,index3:max_level];

J3=origin_j[index3,index3:max_level];

C_A=C1@J2@J3;C_B=J1@C2@J3;C_C=J1@J2@C3;

C_AB=C1@C2@J3;C_AC=C1@J2@C3;C_BC=J1@C2@C3;

C_ABC=C1@C2@C3;

power_c=power[3];

power_ab=power[4];power_ac=power[5];power_bc=power[6];

power_abc=power[7];

end;

/*power*/

%macro pw(c,pw_exp);

n_orig=j(1,q,1);n=j(1,q,1);

if &pw_exp.^=.then do;

if method=1 then do;

test="Wilks' Lambda";

do until (pw>=&pw_exp.);

n=n+n_orig;xx=t(n)#I(q);E=sigma * (n[<>,+]-q);

theta=&C.* m; H=t(theta)*inv((&C.*inv(XX)*t(&C.)))*theta;

T=H+E;df1=a*p;W=det(E*inv(T));fmm=a**2+p**2-5;

if fmm>0 then g=sqrt((a**2*p**2-4)/(a**2+p**2-5)); else g=1;

eta=1-W**inv(g);

df2=g*((n[<>,+]-q)-(p-a+1)/2)-(a*p-2)/2;

if df2>0 then do;

F_statistics=(eta/df1)/((1-eta)/df2);

f_c=finv(1-alpha,df1,df2);lambda=df1*F_statistics;

pw=(1-probf(f_c,df1,df2,lambda))*100; sum_n=n[<>,+];

end;

else pw=0;

end;

end;

if method=2 then do;

test="Pillai-Bartlett Trace";

do until (pw>=&pw_exp.);

n=n+n_orig;xx=t(n)#I(q);E=sigma * (n[<>,+]-q);

theta=&C.* m; H=t(theta)*inv((&C.*inv(XX)*t(&C.)))*theta;

T=H+E;df1=a*p;

ht=h*inv(t);PBT=trace(ht);s=min(a,p);

eta=pbt/s;df2=s*((n[<>,+]-q)-p+s);

if df2>0 then do;

F_statistics=(eta/df1)/((1-eta)/df2);

f_c=finv(1-alpha,df1,df2);lambda=df1*F_statistics;

pw=(1-probf(f_c,df1,df2,lambda))*100; sum_n=n[<>,+];

end;

else pw=0;

end;

end;

if method=3 then do;

test="Hotelling-Lawley Trace";

do until (pw>=&pw_exp.);

n=n+n_orig;xx=t(n)#I(q);E=sigma * (n[<>,+]-q);

theta=&C.* m; H=t(theta)*inv((&C.*inv(XX)*t(&C.)))*theta;

T=H+E;df1=a*p;

he=h*inv(E);hlt=trace(he);

s=min(a,p);eta=(hlt/s)/(1+hlt/s);

df2=s*((n[<>,+]-q)-p-1)+2;

if df2>0 then do;

F_statistics=(eta/df1)/((1-eta)/df2);

f_c=finv(1-alpha,df1,df2);lambda=df1*F_statistics;

pw=(1-probf(f_c,df1,df2,lambda))*100; sum_n=n[<>,+];

end;

else pw=0;

end;

end;

end;

else do; pw=.; sum_n=0; end;

%mend;

/*compute total sample size*/

a=&f_level.[1]-1; %pw(C_A,power_a);sum_n_a=sum_n;Smp_size=sum_n_a;

if f>1 then do;

a=&f_level.[2]-1;%pw(C_B,power_b);sum_n_b=sum_n;

a=(&f_level.[1]-1)*(&f_level.[2]-1);%pw(C_AB,power_ab);

sum_n_ab=sum_n;

Smp_size=j(3,1,.);

Smp_size[1]=sum_n_a;

Smp_size[2]=sum_n_b;

Smp_size[3]=sum_n_ab;

end;

if f>2 then do;

a=&f_level.[3]-1;%pw(C_C,power_c);pw_c=pw;sum_n_c=sum_n;

a=(&f_level.[1]-1)*(&f_level.[3]-1);

%pw(C_AC,power_ac);sum_n_ac=sum_n;

a=(&f_level.[2]-1)*(&f_level.[3]-1);

%pw(C_BC,power_bc);sum_n_bc=sum_n;

a=(&f_level.[1]-1)*(&f_level.[2]-1)*(&f_level.[3]-1);

%pw(C_ABC,power_abc);sum_n_abc=sum_n;

Smp_size=j(7,1,.);

Smp_size[1]=sum_n_a;

Smp_size[2]=sum_n_b;

Smp_size[3]=sum_n;

Smp_size[4]=sum_n_ab;

Smp_size[5]=sum_n_ac;

Smp_size[6]=sum_n_bc;

Smp_size[7]=sum_n_abc;

end;

Total_n=Smp_size[<>,];grp_size=Total_n/q;

/*compute power for total sample size*/

%macro pw2(c,pw_exp);

if &pw_exp.^=.then do;

n=j(1,q,grp_size);xx=t(n)#I(q);E=sigma * (n[<>,+]-q);

theta=&C.* m; H=t(theta)*inv((&C.*inv(XX)*t(&C.)))*theta;

T=H+E;df1=a*p;

if method=1 then do;

W=det(E*inv(T));fmm=a**2+p**2-5;

if fmm>0 then g=sqrt((a**2*p**2-4)/(a**2+p**2-5)); else g=1;

eta=1-W**inv(g);

df2=g*((n[<>,+]-q)-(p-a+1)/2)-(a*p-2)/2;

F_statistics=(eta/df1)/((1-eta)/df2);

end;

if method=2 then do;

ht=h*inv(t);PBT=trace(ht);s=min(a,p);

eta=pbt/s;df2=s*((n[<>,+]-q)-p+s);

F_statistics=(eta/df1)/((1-eta)/df2);

end;

if method=3 then do;

he=h*inv(E);hlt=trace(he);s=min(a,p);

eta=(hlt/s)/(1+hlt/s);df2=s*((n[<>,+]-q)-p-1)+2;

F_statistics=(eta/df1)/((1-eta)/df2);

end;

f_c=finv(1-alpha,df1,df2);lambda=df1*F_statistics;

pw=(1-probf(f_c,df1,df2,lambda))*100;

end;

else pw=.;

%mend;

Level= &f_Level.;

factor="Factor A";

a=&f_level.[1]-1; %pw2(C_A,power_a); pw_a=pw;power=pw_a;Alpha1=alpha;

if f>1 then do;

factor={"Factor A","FactorB","Factor AB"};

a=&f_level.[2]-1; %pw2(C_B,power_b); pw_b=pw;

a=(&f_level.[1]-1)*(&f_level.[2]-1); %pw2(C_AB,power_ab); pw_ab=pw;

power=j(3,1,.);power[1]=pw_a; power[2]=pw_b;power[3]=pw_ab;

Alpha1=j(3,1,alpha);

end;

if f>2 then do;

factor={"Factor A","FactorB","FactorC","FactorAB","FactorAC","FactorBC","Factor ABC"};

a=&f_level.[3]-1; %pw2(C_C,power_c); pw_c=pw;

a=(&f_level.[1]-1)*(&f_level.[3]-1); %pw2(C_AC,power_ac); pw_ac=pw;

a=(&f_level.[2]-1)*(&f_level.[3]-1); %pw2(C_BC,power_bc); pw_bc=pw;

a=(&f_level.[1]-1)*(&f_level.[2]-1)*(&f_level.[3]-1);

%pw2(C_ABC,power_abc);pw_abc=pw;

power=j(7,1,.);power[1]=pw_a; power[2]=pw_b;power[3]=pw_c;

power[4]=pw_ab;power[5]=pw_ac;power[6]=pw_bc;power[7]=pw_abc;

Alpha1=j(7,1,alpha);

end;

Mean_Matrix=&m.;

end;

print test[Label="Test"]

p[Label="Number of Response Variables"]

sd[Label="Common Standard Deviation"]

rho[Label="Correlation"]

grp_size[Label="Group Size"]

Total_n[Label="Total Sample Size"];

Print Factor [label="Factor"]

Level [Label="Level"]

Alpha1 [Label="Alpha"]

Power [Label="Power(%)"];

Print Mean_Matrix;

Print sigma[label="Covariance Matrix"];

finish MGT3;

%let sigma1={3.641 1.274 2.641 4.555,1.274 2.623 1.947 2.722,2.641 1.947 9.548 7.001,4.555 2.722 7.001 15.914};

%let power={80};

run MGT3(0.05,&power.,4,1,.,.,&sigma1.,1);

quit;

SAS 9.4运行结果：

图1-68 SAS 9.4关于例1-28样本量估计的参数设置与计算结果