地铁车辆段接触网感应电压研究

魏 巍

(中铁第四勘察设计院集团有限公司，武汉430063)

0 引言

近年来，由于车辆段内股道分布密集，接触网距离较近，带电接触网会对邻近线产生感应影响。一般来说，接触网对四周导体的影响可以分为静电感应(容性耦合)和电磁感应(感性耦合)，但对于直流牵引供电系统来说，只需考虑静电感应影响即可。

当国内多条地铁在车辆段库内或正线上陆续出现接触网停电问题时，相邻线会存在较高电压或本线存在残留电压等，容易对运营维护人员心理产生较大的负面影响。

带电的强电输电线在其周围能形成强大的静电场，邻近线路就处于这个静电场中，线路与大地以及线路与强电输电线之间形成耦合电容，被感应形成静电感应电压。这种现象叫做容性耦合，也叫做静电感应影响。地铁车辆段接触网通过静电感应在邻近线路上产生静电感应电压。

两根平行导线间静电感应电压可以利用经典电磁场理论进行求解，也可以利用经验公式进行求解。

1 电磁场理论法

导线的空间分布如图1所示。

图1中，导线1、2为相互平行的接触网导线，导线1为带电导线，导线2为邻近的被感应的导线，导线1'为导线1相对于大地表面的镜像。

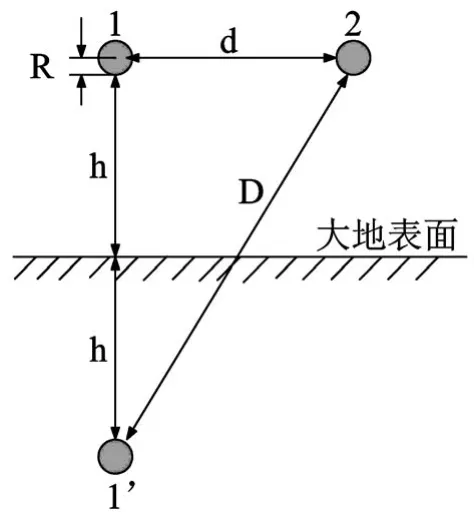
图1 导线空间分布示意1

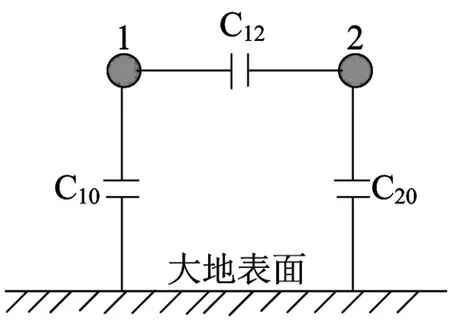
图2 导线空间分布示意2

接触网上的静电感应电压是通过接触网带电导线之间的部分电容耦合产生的，如图2。由文献[1]中部分电容的概念，计算出导线1、2之间以及两导线与大地之间的电容，可以得出[1]:

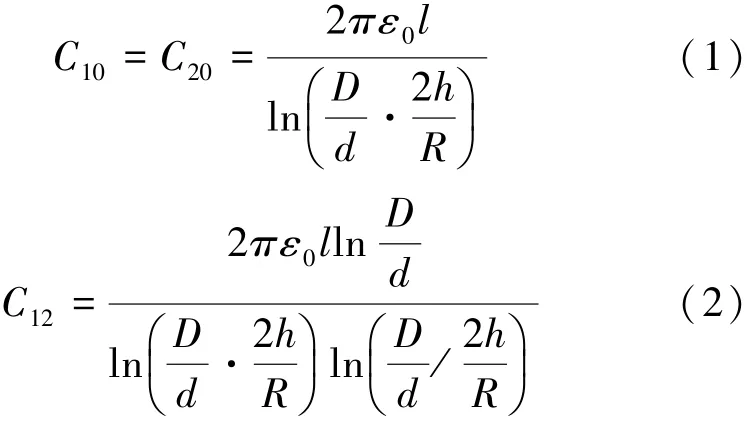
式中，ε0为真空介电常数(8.85×10-12F/m)，l为导线的并行长度(m)，h为导线及其镜像到地面的距离(m)，R为导线的半径(m)，D为导线2与导线1的镜像1'的中心距离(m)，d为导线1与导线2的中心距离(m)。

解图2中的电容电路可得导线1在导线2上产生的静电感应电压为:

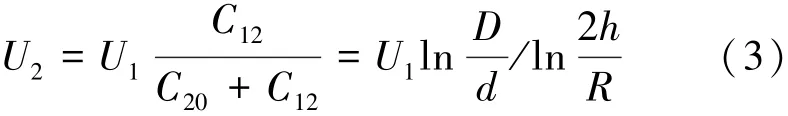
式中，U1为接触网网压，V；U2为处于接触网静电感应范围内的金属导线上的静电感应电压，V。

根据车辆段内接触网分布的实际情况以及线索参数，可以计算出感应电压。以某车辆段为例，股道架空接触网间距4.6m，架空接触网导高5m，供电电压1 500V。

取h＝5m，R＝0.0 046m，d＝4.6m，U1＝1 500V，则D＝11m，带入式(3)解得:静电感应电压U2＝170.22V。

由式(3)可知，静电感应电压与两线的平行长度无关，与接触网中有无电流无关，其大小主要取决于平行导线的间距和导线的电压。导线间距越小，接触网导线电压越高，产生的静电感应电压越大。

2 经验公式法

由文献[2]可知，处于接触网静电感应范围内的金属导线上的静电感应电压的通用计算式为:

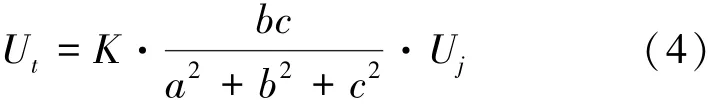
式中，Ut为处于接触网静电感应范围内的金属导线上的静电感应电压，V；Uj为接触网网压，V；a为接触网与金属导线的水平距离，m；b为接触网对地的平均距离，m；c为架空金属导线的对地高度，m；K为计算系数；R为接触网线索的等效半径，m。

一般情况下，计算系数K在单线区段取为0.4，在复线区段取为 0.6，简单悬挂计算系数取为0.263[2]。现根据车辆段内接触网分布的实际情况以及线索参数，计算出感应电压。

取a＝4.6m，b＝5m，c＝5m，R＝0.0 046m，Uj＝1 500V，则通过式(5)计算得出计算系数K＝0.26。

代入式(4)解得:静电感应电压Ut＝137V。

3 结束语

对于地铁1 500V柔性悬挂接触网，当取导线间距4.6m、导高5m、导线计算半径0.0 046m时，用经典电磁场理论计算得出的静电感应电压为170.22V，用经验公式计算得出的静电感应电压为137V，二者相差不大。

国际标准IEC62128-1[3]规定，长时工况下人体可接触电压限值为60V，地铁车辆段接触网静电感应电压远超过限值，会给运营维护人员带来安全隐患。

接触网在停电检修时，验电发现有电压属正常现象。此时若直接悬挂临时地线，产生的瞬时电流会带来安全隐患，应先接地线再挂底线，方可上网作业。这样不仅可保证接触网误送电时检修人员的安全，而且可消除邻线接触网带电时对它的静电感应电压。