一种负载型四足步行平台复杂地形静步态行走位姿调整方法

晁智强， 谭永营， 王 飞， 宁初明

(1.陆军装甲兵学院车辆工程系， 北京 100072； 2. 66366部队, 河北 高碑店 074000；3. 军事科学院系统工程研究院, 北京 100039)

负载型四足步行平台以其良好的复杂地形适应能力得到人们的关注。在复杂环境中，四足步行平台的静步态是其行走的主要步态之一。由于自然环境的复杂性及结构的限制，步行平台静步态行走过程中要不断调整姿态，以适应复杂地形。由于负载型四足步行平台机身质量大、质心位置高、惯量大，因此位姿调整对于其复杂地形的适应性有重要影响。

四足步行平台复杂地形适应能力由其足端活动空间及地形坎坷程度共同决定，在其静步态行走过程中足端必须满足活动空间的需求，否则无法实现期望的位姿。国内外学者对四足步行平台位姿调整方法进行了分析，如：KALAKRISHNAN等[1]为实现Littledog复杂地形静步态行走，在最大化足端可达性和避免步行平台与地形干涉的基础上，设计了Pose Finder对其目标姿态进行搜索，但这种方法需要消耗大量的时间，限制了步行平台的移动速度；WINKER等[2]为Hydraulically Actuated Quadruped Robot步行平台设计了Body Pose Finder，根据足端在机体坐标系中的高度确定平台的高度，由前后腿及左右腿高度差确定步行平台的俯仰角与横滚角,但这种方法需要提前得到复杂地形的特征；孟健等[3]在对四足步行平台斜坡及台阶行走姿态调整问题的研究中，指出步行平台的姿态由支撑腿形成的支撑面决定，张帅帅等[4]则给出了四足步行平台以间歇静步态在复杂地形行走时的目标姿态角，但二者均对姿态调整过程中足端活动空间问题考虑不足，这容易导致步行平台运动过程中达到结构死点，造成平台失去稳定性。

为满足四足平行平台行走过程中实时调整姿态的需要，笔者在步行平台足端活动空间分析的基础上，综合考虑感受到的地形特征及步态参数，得到其目标姿态角，且对姿态调整过程进行规划，保证了平台静步态行走过程中轨迹的连续性，最后对步行平台复杂地形静步态行走进行仿真，验证了位姿调整方法的有效性。

1 四足步行平台运动学分析及足端活动空间

四足步行平台的模型及各坐标系如图1中所示，其4条腿的结构完全相同，每条腿有3个自由度，从上到下依次为胯侧摆段、大腿段和小腿段，对应的关节分别为胯侧摆关节、胯纵摆关节和膝关节，且均为主动关节。

为方便对步行平台机体及各腿段位姿的分析，在其机体质心处建立机体坐标系，在各腿胯侧摆关节处建立各腿基坐标系，并选择大地上任一点建立绝对坐标系。机体坐标系的xb轴指向平台前进方向，yb指向其侧方向，zb轴指向竖直方向。各腿基坐标系坐标轴的指向与机体坐标系相同。步行平台参数如表1所示。

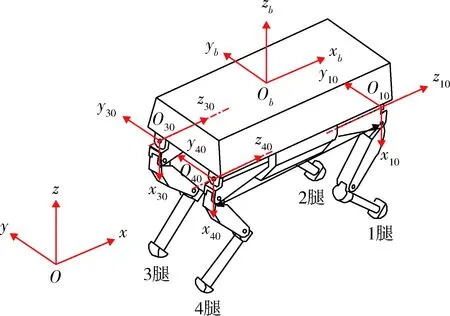
图1 步行平台模型及各坐标系

参数数值机体质量M/kg150髋侧摆段长度l1/m0.085大腿长度l2/m0.31小腿长度l3/m0.3

由于各腿结构相同，因此仅对右前腿进行运动学分析。运用Denavit-Hartenberg方法进行步行平台单腿的运动学分析，在各驱动关节及足端建立如图2所示的坐标系[5]。

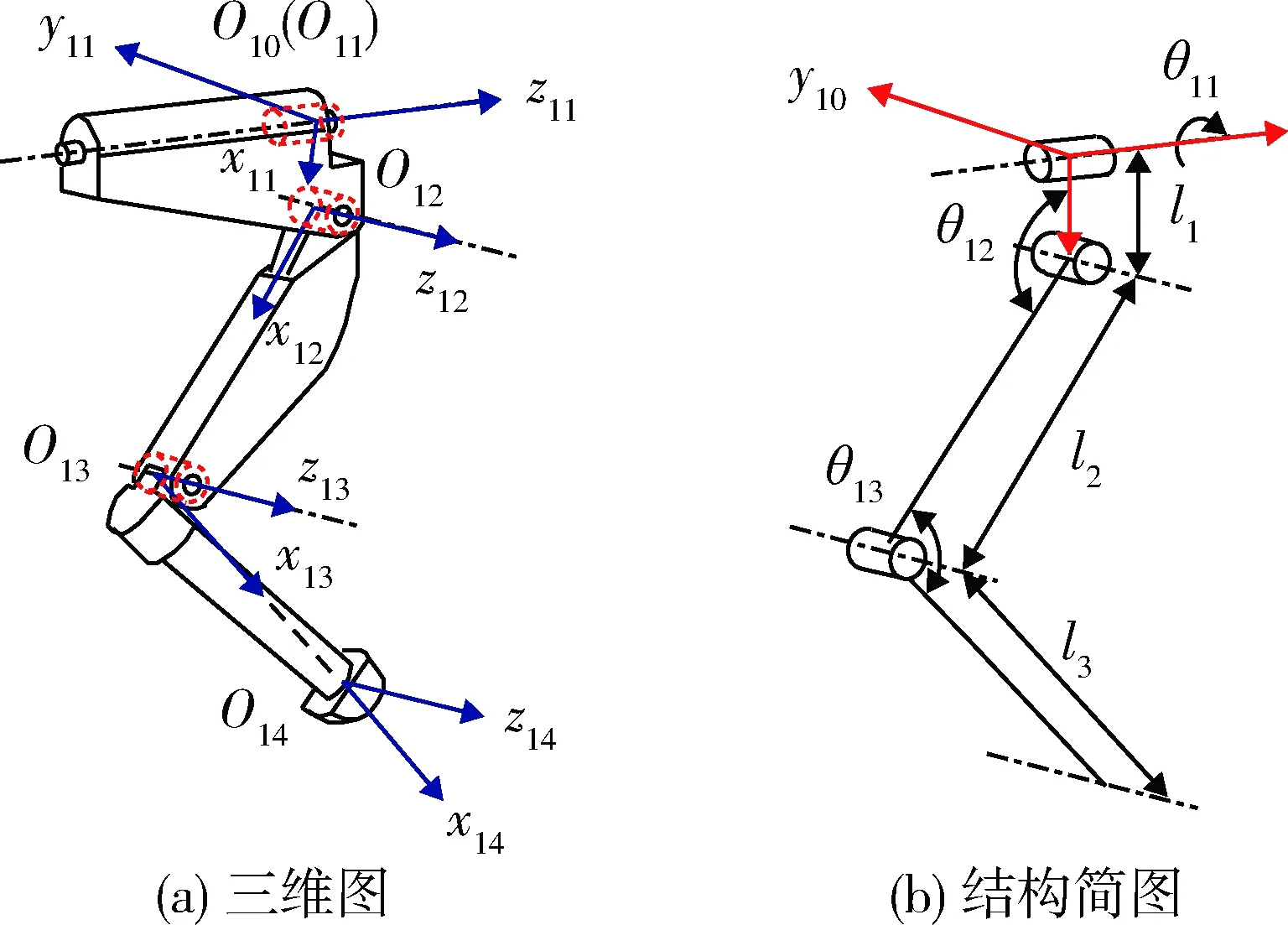
图2 步行平台模型及各坐标系

由旋转变换矩阵连乘可得1腿足端在腿基坐标系中的坐标为

(1)

式中：θ11为1腿胯侧摆关节转角；θ12为胯侧摆段与大腿夹角；θ13为大腿与小腿夹角。将式(1)对时间求导，可得

(2)

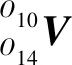
四足步行平台的足端活动空间是指在其机械结构约束下足端所能达到的活动范围[7]。足端活动空间在步行平台机械结构设计时具有重要作用，是步行平台腿部杆件设计的重要参考标准。由于步行平台静步态行走过程中并不转弯行走，腿在侧向的摆动较小，因此在单腿平面内对步行平台足端活动空间进行分析即可满足要求。平台胯纵摆关节的活动范围为90°～160°，膝关节转角变化范围均为50°～130°，结合腿部的正运动学分析，可得出单腿平面内其足端活动空间，如图3红色区域所示。

图3 足端活动空间

由动物仿生学研究可知：步行动物在运动过程中前后腿的运动呈现出明显的对称现象[8]。由于四足步行平台各腿在机体的安装方式为前肘后膝，前后腿成镜像对称关系。因此,为方便对步行平台行走过程中足端的运动进行研究，选定的足端活动空间为图3蓝色区域。

2 四足步行平台目标姿态的选择

四足步行平台姿态调整过程中其目标姿态由平台自身结构及地形共同决定。对于腿部各腿段较长，足端活动空间较大的步行平台，在通过一些高度较低障碍时，可以不调整机体姿态，充分利用较大的足端活动空间实现对障碍的跨越。但对于文中的负载型四足步行平台，受足端活动空间的限制，必须进行姿态调整，才能实现对障碍的爬越。

2.1 基于支撑平面的步行平台地形感知

张帅帅等[4]提出了利用支撑腿足端坐标平均值计算目标俯仰角的方法，实现了平台间歇静步态对复杂地形的适应性；CHEW等[9]针对双足步行平台上斜坡问题，提出了利用广义坡度(global slope)和局部坡度(local slope)计算步行平台的相关参数。在参考文献[4]、[9]的基础上，借助四足支撑过程中支撑腿形成的平均支撑平面的法向量，可计算得到步行平台感受到的地形坡度，具体方法如下：

图4为四足步行平台地形坡度计算示意图。1腿足端与2腿足端连线中点BWp12及3腿足端与4腿足端连线中点BWp34在平面xBWOBzBW内的投影分别为

(3)

(4)

图4 地形坡度计算示意图

1腿足端与4腿足端连线中点BWp14及2腿足端与3腿足端连线中点BWp23在yBWOBzBW平面内的投影分别为

(5)

(6)

设a=(BWx34-BWx12,BWz34-BWz12)，b=(BWx23-BWx14,BWz23-BWz14)，则由向量a与b决定的平面法向量为

(7)

步行平台姿态角与n的关系为

(8)

式中：θ为a与b的夹角；α为步行平台偏航角，根据四足步行平台行走过程实际进行设置；βd、γd分别为地形前进方向坡度和侧向坡度，二者均为待求量；Rz(α)、Ry(βd)、Rx(γd)为相应姿态角的旋转变换矩阵。则

(9)

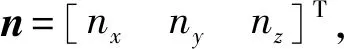
(10)

四足步行平台静步态行走过程中，根据以上各式可得平台感受到的地形特征。

2.2 步行平台目标位姿确定

四足步行平台复杂地形行走过程中位姿调整的目的，是满足下一阶段平台行走过程中足端的运动需求，避免死点位置，同时充分利用其活动空间提高复杂地形适应能力。因此，结合平台行走过程中足端的运动需求对其活动空间进行分析。

四足步行平台静步态行走过程中，为充分利用支撑多边形中的双支撑三角形，实现单侧腿的连续迈步，选择的迈腿顺序为3腿→2腿→4腿→1腿，其中在2腿及1腿迈腿结束后为四足支撑重心调整阶段。步行平台的位姿调整过程可能存在于任何一个摆动腿的着地之后。当步行平台感受到的地形坡度超过设定的阈值后，就进入姿态调整阶段，之后进行四足支撑重心位置调整，最后进入正常的步态周期。

由步行平台绝对稳定裕度定义可知：其静步态行走过程中的稳定性由重心到支撑多边形边界的距离决定[10]。而步行平台在复杂地形行走过程中，稳定裕度的大小往往是在其重心的水平投影坐标系中描述的，因此，在图4坐标系OBxBWyBWzBW内中对步行平台足端的运动学裕度进行分析。黄博等[11]提出当步行平台机体的姿态与地形平行时，其足端的运动裕度最大，灵活性最好。因此，在足端活动空间分析过程中以感受到的地形坡度为约束条件。

根据四足步行平台行走过程中相对跨距、步高等相关步态参数及摆动腿足端轨迹可得其足端步态参数三角形，如图5所示。其中：lx为步行平台下一步迈腿的相对跨距；H为步行平台的迈腿高度。

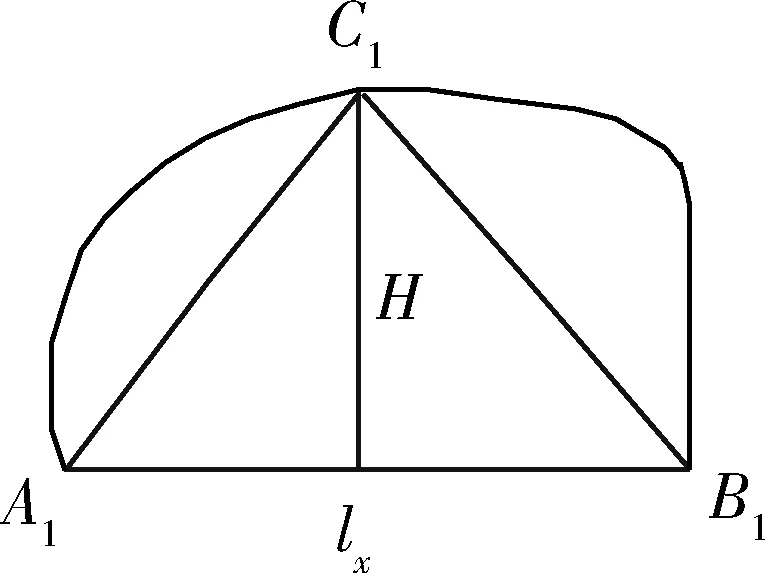
图5 步态三角形

四足步行平台足端活动空间分析主要是在给定期望姿态角情况下，寻找摆动腿可能的起步点位置及对姿态角进行校正。具体过程如下：

1) 利用步态参数三角形的下底，在选定的足端活动空间中找到能够满足要求的足端最下方位置，如图6中GN。起步点的位置必须在直线GN的上方。

图6 起步点位置

2) 利用步态参数三角形起步点位置(A1)及最高点位置(C1)，在选定的足端活动空间中找到满足迈腿高度及相对跨距的最左端位置E。起步点位置必须在点E的右侧。

3) 过点E做直线AB的平行线，如图6中EF。起步点位置必须在直线EF的下方。

4)利用步态参数三角形在足端活动空间找到能够满足迈腿相对跨距及摆腿高度的起步点最右端位置J。

z=lEF(x)=lAB(x)-(H-lxtanφyd)cosφyd，

(11)

式中：φyd为目标俯仰角。

由步态参数三角形及选定足端活动空间特征点可得点E在坐标系OBxByBzB中纵坐标为

zE=zB-(H-lxtanφyd)cosφyd。

(12)

点E横坐标可由直线lEF(x)与五次曲线lBC(x)交点得到，

xE=lEF-BC(zE)，

(13)

式中：lEF-BC(zE)表示2个方程的交点。则在坐标系OBxBWyBWzBW中E点的坐标可由坐标变换得到。位姿调整结束后，步行平台接着进行四足支撑阶段，机体前进方向的位移量由下一摆动腿的运动学裕度决定。因此，为保证在正常的步态周期中机体能够一直保持前进，还需对机体的位置进行调整。

由于四足步行平台的高度不可能太小，由上述方法得到的步行平台机体高度不一定满足平台最小高度要求。因此，若不满足上述约束条件，则减小相对跨距，增大姿态角，运用相同的方法重新寻找起步点位置。

3 四足步行平台机体位姿调整过程分析

相关研究表明：四足步行平台复杂地形行走过程中失稳的原因往往是驱动关节达到了死点位置，使其支撑力不足[12]。当将机体位姿调整阶段与步态规划阶段放在一起时，机体姿态角的变化范围较大，不利于负载型步行平台机体稳定性，在此单独设置机体姿态调整阶段。且在机体姿态调整过程中，为避免前后方向及侧方向的运动对其机体位姿调整的影响，将步行平台机体的速度减到0后再进行机体姿态的调整。因此，步行平台的位姿调整过程可分为3个阶段，分别为减速阶段、姿态调整阶段及调整后的重新规划阶段。

3.1 减速阶段

减速阶段主要是在姿态调整前将步行平台前进方向及侧方向的速度减小到0，避免姿态调整过程中各关节达到死点位置。为保证平台机体轨迹的连续性，用三次多项式对步行平台的机体速度进行规划。在此过程中，机体俯仰角保持不变，重心移动速度的约束条件为

(14)

(15)

式中：vx(·)、vy(·)分别为步行平台机体前进方向和侧向的速度；ax(·)、ay(·)分别为步行平台机体前进方向和侧向的加速度；vx0、vy0分别为步行平台前进方向及侧方向的初始速度；tc1为减速过程所用时间。将以上约束条件代入三次多项式中，可得

(16)

3.2 姿态调整阶段

在四足步行平台的速度减小到0后，接着对其姿态进行调整。在姿态调整过程中，希望其由初始姿态角平稳变化到目标姿态角。因此，为保证速度及加速度连续，运用五次曲线对其姿态调整过程中俯仰角进行规划。其满足的边界条件为

(17)

(18)

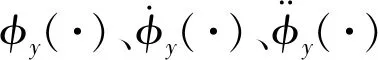
(19)

3.3 调整后重新规划阶段

姿态调整结束后，为保证下一摆动腿的运动学裕度不小于参考值Mac，机体需在前进方向调整位置，以避免正常行走过程中机体后退现象。假设此过程机体在前进方向的调整量为xb2，机体在减速阶段的位移量为xb1,则此过程约束条件为

(20)

(21)

式中:x(·)为平台在前进方向的位置。对相关参数进行求解，可得

(22)

4 四足步行平台静步态行走位姿调整仿真

构建的复杂地形及四足步行平台三维模型如图7所示，机体装配陀螺仪以实现姿态的感知，足底装有力传感器。为验证位姿调整方法的有效性，设计了如图7所示的复杂地形。四足步行平台对地形未知，完全依靠足底力传感器实现对地形的适应。在步行平台行走过程中，其相关参数的变化图8-10所示。

图7 构建的复杂地形及四足步行平台三维模型

由图8可知:四足步行平台复杂地形行走过程中共有4次姿态调整过程，除姿态调整过程外，其余时刻机体的速度均>0。由图9可知:步行平台姿态调整过程中，机体俯仰角与前进速度按照预先规划好的轨迹连续变化。由图10可知:在平台行走过程中，足端始终在其活动空间中。步行平台利用文中的姿态调整方法实现了复杂地形中平稳行走，仿真结果证明了位姿调整方法的有效性。

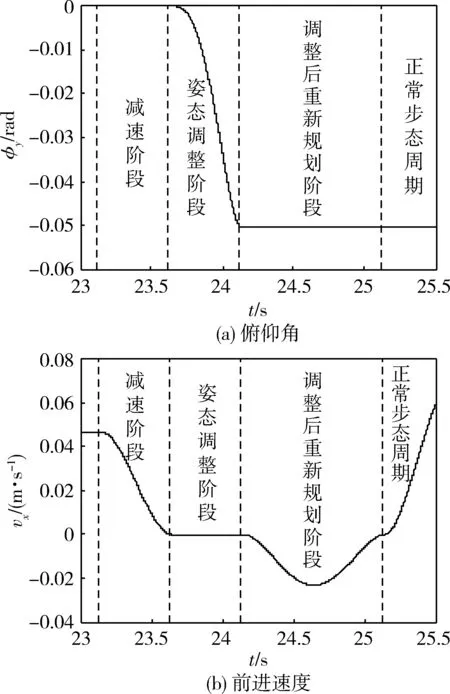
图9 某个姿态调整过程的前进速度及俯仰角

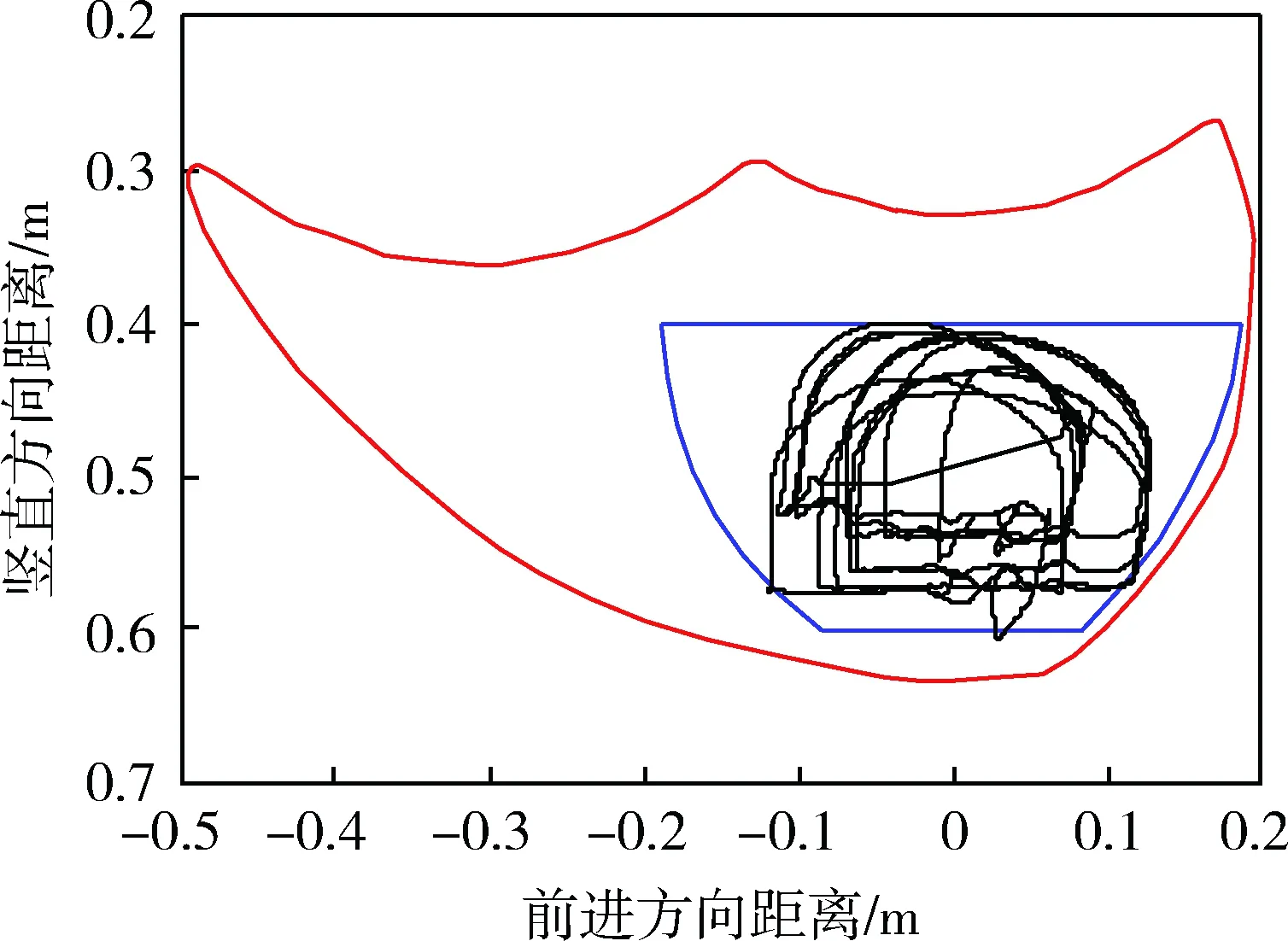
图10 右前腿足端活动情况

5 结论

笔者对负载型四足步行平台静步态行走过程中位姿调整方法进行了研究，对目标姿态的选择及位姿调整过程进行了分析，并对位姿调整过程进行了仿真验证，结果表明：负载型四足步行平台分阶段的姿态调整方法实现了其在复杂地形中的平稳行走。负载型四足步行平台是一个复杂的多体动力学系统，笔者在研究过程中仅考虑了机体俯仰角的变化，后续将研究此方法在平台同时出现俯仰角及横滚角时的适用性。