开展数学写作研究，促进错题深度订正*

☉江苏省南京市莲花实验学校 吉明华

利用数学写作促进学生数学学习的研究得到很多一线教师的喜欢，不少数学期刊也经常有类似的研究心得的文献，研究者们关注的往往是数学写作的类型（如数学小论文、数学日记、数学周记、数学作文、数学反思小文章等），而对数学写作的功能特点的探讨泛泛而谈偏多，缺少更为细化、更有针对性的功能特点的研究.本文先分享近期收集到的七年级学生数学写作案例，并主题关注数学写作如何促进错题深度订正.

一、学生围绕听课笔记梳理而成的数学写作案例与评析

案例1：《知其然，知其所以然》，七年级学生Z.

今天上课老师主要讲评了单元测验试卷，题目多数是老师以前就讲过的，没考好的原因主要集中在粗心上.

虽然下面这道题练过、讲过多次，我还是错了.反复思考，我觉得这道考题很有意思.

已知，a、b在数轴上的位置如图1所示，化简|a|-|a-b|＋2|a＋b|.

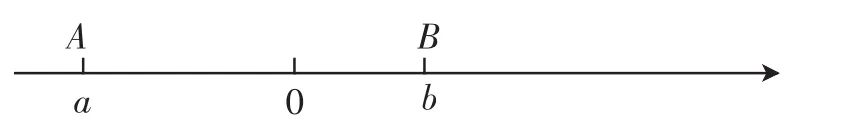
图1

看着这一个个绝对值符号，我仿佛看到了不可跨越的长城.不过试卷上的长城，只要掌握技巧，便可轻松跃过，经常在这种题目上跌倒的我立刻敲响警钟，努力回忆老师讲的解法步骤.

第一，“明敌军主力”，判断绝对值符号内结果的正负.

由图可知，a＜0，b＞0，|a|＞|b|，所以a＜0，a-b＜0，a＋b＜0.

第二，“哭长城”，去绝对值号.我们要拿出孟姜女的精神，让长城不再那么坚固，同时我们要使用“留白艺术”，每个绝对值内都是负数，那么先把绝对值改为小括号，再在前面添加负号，此时绝对值外所有部分都还未添加，“留白”是为了给它们空出位置，现在要将它们补上去了，再适当添加中括号.

第三，“清理废墟”，最后就剩下化简了，运用去括号的规律，再合并同类项，便可得到答案

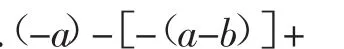
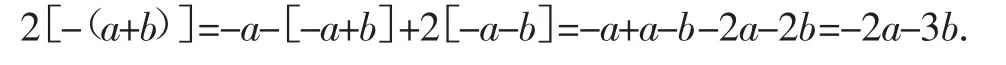
“长城之战”，考生获得胜利！

老师评析：Z同学这篇生动形象的“攻破长城”主要关注的是绝对值符号化简问题，这是一类高频问题、必考题型，不但有效考查绝对值的概念，又对添括号、去括号、合并同类项等技能有“综合”要求.可以说，一份七上期中试卷往往因为这种题型的出现，就能“阻挡”相当一部分学生向高目标分挑战.

Z同学用“三部曲”化解难点，形象生动，这就是“明敌军主力”：判断绝对值符号内字母或式的正负；“哭倒长城”：化去绝对值；“清理废墟”：化简结果.

只要能严格执行她提出的这个“三部曲”，这类问题一般都能顺利求解.我们看到的很多错例中，在“三部曲”的每一步都有学生出错，从而导致解题失败，是值得学习者认真体会的.

特别欣赏的是，关于去绝对值符号这一步骤的讲解，小作者使用了不同颜色进行书写表达，并提醒“留白”渐次生成，这些不正是很多数学教育家们所倡导的“数学活动经验”吗？

从数学求真的角度看绝对值符号如何向小括号转化这一步骤，需要“回到概念”，认真想清绝对值的定义、几何意义，就知道化去绝对值符号后要成为“非负数”，这需要对绝对值符号内的数、字母或式子的正负有精准辨析，据此就沟通了第一步与第二步，“三部曲”也就浑然一体，不可分割.理解这点，就从简单的“三部曲”能做对习题“知其然”层次，走上了深刻理解的“知其所以然”的境界了！

案例2：《学好数学要有“序”》，七年级学生T.

数学是一门奇妙的学科，说它容易却有点儿难，说它难却又很简单、好懂.它有各式各样的表达形式，只要我们学懂了概念，掌握了方法，就会觉得很轻松，很多问题其实是换汤不换药.学好数学不能只掌握方法，还要有敏锐的洞察力、缜密的思维和细心的计算，例如，最近学习的整式的加减，我还是有一些化简方面的错误，究其原因，主要是读题太快，跳步太多，所以我要在这篇数学写作中对一些化简上的错误做一些反思.比如，认真读题后，不能无目的化简，要做到“有序”思考，当然还可以做上不同的记号，以便帮助我们正确进行整式的化简运算.

比如：a＋b＋c-b＋c.

如果直接合并，容易看漏、看错，可以先做上标记，如下：

=a＋（b-b）＋（c＋c）

=a＋2c.

有些时候，除了计算的“序”，还要注意数字或字母书写上的规范，比如，有人容易把数字5写成3，或者x与z的书写字体不当，还有些同学把字母b写成数字6之类的.

当然，还有一些策略，如数字与符号之间适当空一点距离，不要写得过分“密集”或者“密不透气”.

1905年Schulthess依据脊柱X线冠状面上侧弯的部位及数目首先将特发性脊柱侧凸分为5型：颈部和胸部弯、胸部弯、胸部和腰部弯、腰部弯和双主弯[5]，随后Lonstein等[6]和Winter等[7]将其分为7型：单胸弯、单胸腰弯、单腰弯、双胸弯、胸弯和腰弯、胸弯和胸腰弯、3个或以上的多弯，以上的分型是根据侧凸的在X线上直观的形态，并未与临床治疗及手术融合进行结合。

老师评析：T同学在《学好数学要有“序”》中，结合简单的合并同类项讲解了计算有“序”的步骤分解，值得一些喜好“跳步骤”的学生倾听.此外，他还小结了很多非智力因素中的运算错漏，如数字5的书写不规范；对字母b与数字6辨识不清；字母x与z的书写字体不当出错；对a＋b-c书写字符间距的提醒，等等.以上都是课堂板演或老师讲解时提到的一些究错细节，足以说明T同学课堂捕捉力之细致，非常难得！

案例3：《解题过程的严谨与全面》，学生L.

一眨眼，单元测试又到了，对于这次考试的错题，我也有分析，做错的题目为“对于任意有理数x，比较多项式4x2-5x＋2与3x2-5x-2的值的大小”.

读完题目，我便知道，如果运用“作差法”便会轻易地求出结果.于是，便有了如下的过程：

解：（4x2-5x＋2）-（3x2-5x-2）

=4x2-5x＋2-3x2＋5x＋2

=x2＋4.

因为x2＋4＞0，所以4x2-5x＋2＞3x2-5x-2.

自认为万无一失的我却在批改后的试卷上看到了扣掉的分数.于是满心疑惑，便认真地对照了老师的解答过程：

解：设4x2-5x＋2=A，3x2-5x-2=B.

A-B=（4x2-5x＋2）-（3x2-5x-2）

=4x2-5x＋2-3x2＋5x＋2

=x2＋4.

因为x2≥0，所以x2＋4＞0，所以4x2-5x＋2＞3x2-5x-2.

所以A＞B.

相比较后，我发现与老师的不同点只有2处，一是开头的“设4x2-5x＋2=A，3x2-5x-2=B”，二是末尾“因为x2≥0，所以x2＋4＞0”，短短两行，到底有多大的奥秘呢？

我思考起来.开头的“设4x2-5x＋2=A，3x2-5x-2=B”,不仅可以使下面的“作差法”来得简洁、工整，还可以直接明了地让人理解过程的用意.而末尾的“因为x2≥0，所以x2＋4＞0”更能解释为什么“x2＋4＞0”.这样的过程相对来说更全面，更严谨，也更值得我们学习.

因此，下一次我在做题时，不仅要讲究思路和方法，还要写好解题过程，尽可能做好我的“严谨与全面”.

老师评析：L同学的数学成绩在班级中名列前茅，所以在批阅作业时对她的过程表达提出了很高的要求.从她这篇数学写作来看，她对比老师的过程表示，“看”出了不同，“看”出了优化的必要，非常有意义.事实上，对于平时的测评、反馈、阅卷来说，扣分并不是目的，而是通过评价促进学生修补错漏、改进方法.教学经验告诉我们，有相当一部分学生并不能如L同学那样仔细对比自己的解法与老师解法的不同，特别是辨别一些细微、细节上的表达差异，他们往往认为“差不多”，结果好像都一样，过程少一两步就不写了.这种“差不多”的认识是要不得的，也是这类学生与优秀学生不断拉开距离的一些重要原因.

二、让数学写作促进学生对错题的深度订正

根据教学经验，整理错题是学好数学的关键，但是如何整理错题是一个大的难题，怎样整理错题才是有效的呢？我们的实践表明：数学写作是促进学生深度订正、整理错题的一个有效途径.

1.用数学写作开展错题订正促进学生深度究错

究错，不仅仅是纠错，更要探究错误，从过程到结果，每一步都像是在下棋，一步出错，满盘皆输.所以找到错误的原因才能实现“病从根本治”.通过数学写作方式，引导学生找出错误，并跟进思考当时为什么错，是哪一步想错了，是概念不清楚，还是计算跳步骤，是否还有不同的解法……把这些逐项分析，就会得到更深刻的理解.有时还可以让学生通过数学写作记录对比老师的解题过程，把初始错误或不够优化的解题步骤也写在旁边，通过对比发现自己解题的欠缺，学会提炼其中精华，防止下次遇到类似问题时再出差错.

2.批阅数学写作可反馈学生对错题的理解深度.

教师批阅学生数学写作时，可以反馈学生对错题的理解深度，也常常能看出学生分析错题进程中“火热的思考”，有利于进一步精准诊评学生对错题是否真正弄懂、达到深刻理解的程度.华东师大终身教授钟启泉先生倡导“对话教学”，不仅是课堂上的对话（“课上对话”）与互动，笔者认为，开展数学写作研究也是对话教学的一种“课下对话”.具体地说，以上文提供的学生数学写作为例，我们在批阅之后都及时给出了评析（有时也是赏析），这就是一种积极的师生对话方式，既肯定学生对错题的理解角度与深度，又对其进行激励、表扬，达到了巩固知识、训练技能、提振学习信心和激发兴趣的多重功能.

三、写在后面

最近几年来，笔者一直开展学生数学写作实践研究，拍照、扫描收集存档了大量学生数学写作，多数常态化的学生数学写作作品虽然达不到直接发表的标准，但是常常查阅会为学生数学写作中偶尔有一两句精彩的观点而高兴，并且会在后续教学中向学生推广这些精彩的反思观点或深刻的解题经验，每每此时，那些被提及（引用）的学生就会非常兴奋，觉得自己在数学写作中某些观点被老师引用，坐姿更加端正，听课更加专注，课后有时又能提交一篇“文以载道”的优秀写作.这事实上也激励着我们持续开展这项“非功利”（看似与应试提分无直接联系）的实践研究，也期待有更多同行能充分利用数学写作这种学习方式，促进学生的数学学习.