基于改进卷积神经网络的多标记分类算法

余鹰，王乐为，吴新念，伍国华，张远健

（1. 华东交通大学 软件学院，江西 南昌 330013; 2. 中南大学 交通运输工程学院，湖南 长沙 410000; 3. 同济大学计算机科学与技术系，上海 201804）

不同于传统的单标记学习问题，多标记学习考虑一个对象对应多个类别标记的情况。例如：一个基因可能同时具有多种功能，如新陈代谢、转录以及蛋白质合成；一首乐曲可能传达了多种信息，如钢琴、古典音乐和莫扎特等；一幅图像可能同时属于多个类别，如motor、person与car等。早期，多标记学习的研究主要集中于文本分类中遇到的多义性问题。经过近十年的发展，多标记学习已成为当前国际机器学习领域研究的热点问题之一，逐渐在情感分类[1]、图像视频语义标注[2]、生物信息学[3]和个性化推荐[4]等实际应用中扮演重要的角色。随着相关应用的发展及需求的不断提升，多标记学习技术的大规模应用仍然要应对很多的问题和挑战。当前在多标记学习领域，特征表达大多采用人工设计的方式，如SIFT、HOG等，这些特征在特定类型对象中能够达到较好的识别效果，但这些算法提取的只是一些低层次(low-level)特征，抽象程度不高，包含的可区分性信息不足，对于分类来说无法提供更多有价值的语义信息，影响分类的精度。目前，如何让多标记系统学会辨别底层数据中隐含的区分性因素，自动学习更抽象和有效的特征已成为制约多标记学习研究进一步深入的瓶颈。

近年来，深度学习在图像分类和目标检测等领域取得了突破性进展，成为目前最有效的特征自动学习方法。文献[5]将传统人工设计的特征与深度神经网络自学习的特征进行了比较，发现后者更有助于提升图像自动标注算法的性能。深度学习模型具有强大的表征和建模能力，通过监督或非监督的方式，逐层自动地学习目标的特征表示，将原始数据经过一系列非线性变换，生成高层次的抽象表示，避免了手工设计特征的烦琐低效。本文针对多标记学习中存在的特征抽象层次不高的问题，利用包含多个隐含层的深度卷积神经网络直接从原始输入中学习并构建多层的分级特征，形成更加抽象的高层表示，实现以最少和最有效的特征来表达原始信息。同时，针对卷积神经网络预测精度高但运算速度慢的特点，利用迁移学习和双通道神经元方法，缩减网络的参数量，提高训练速度，在一定程度上弥补了卷积神经网络计算量大、速度较慢的缺陷。

1 相关工作

1.1 多标记学习

为了便于叙述，在分析之前先给出多标记问题的形式化定义。令 X ={x1,x2,···,xm} 代表实例空间， L ={l1,l2,···,lq} 代表所有标记的集合，Y ={y1,y2,···,ym} 代 表标记空间， T = {(xi,yi)|1 ≤ i ≤ m } 代表训练集。多标记分类的任务就是用训练集T对模型进行训练，使模型学得函数f：X→Y，其中xi∈X表示一个实例，yi∈Y表示实例xi所含有的类别标记，且yi为标记集合L的一个子集。训练完成后，将未分类的数据输入模型，得到与实际标记最大程度接近的分类结果。

目前，多标记分类算法根据解决问题方式的不同，可归为问题转换型和算法适应型两类[6]。问题转换型是将多标记分类问题转化为多个单标记分类问题，如算法BR(binary relevance)[7]、LP(label powerset)[8]等，然后利用单标记分类方法进行处理。算法适应型则是改进已有的单标记分类算法，使其适应于多标记分类问题，如算法BSVM(biased support vector machine)[9]、ML-KNN(multi-label k-nearest neighbor)[10]等。随着深度学习的兴起，已有一些学者开始基于深度学习研究多标记分类问题，Zhang[11]由传统径向基函数RBF(radial basis function)推导出了一种基于神经网络的多标记学习算法ML-RBF。Wang等[12]将卷积神经网络CNN(convolutional neural network)和循环神经网络RNN(recurrent neuron network)相结合，提出了一种多标记学习的复合型框架，用于解决多标记图像分类问题，但这些算法的精度和时间复杂度都有待进一步提升。

1.2 卷积神经网络

卷积神经网络CNN是一种深度神经网络模型，主要由卷积层、池化层和全连接层构成，如图1所示。卷积层负责图像特征提取，池化层用于降维及实现不变形，而全连接层则起到分类器的作用。卷积层和池化层一般作为组合多次成对出现，也可以根据实际情况灵活使用，如AlexNet[13]和VGG[14]。

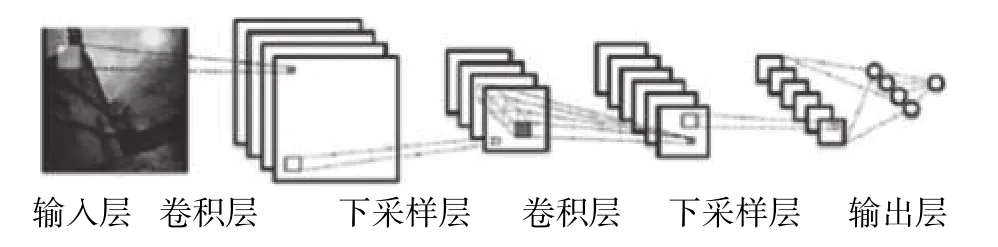
图 1 卷积神经网络结构Fig. 1 Convolutional neural network structure

相比于传统的特征提取方法，卷积神经网络不需要事先人工设定特征，而是通过网络模型从大量数据中自动学习特征表示。通过多层非线性映射，逐层提取信息，最底层从像素级原始数据学习滤波器，刻画局部边缘和纹理特征；中层滤波器对各种边缘滤波器进行组合后，描述不同类型的局部特征；最高层描述整体全局特征。

1.3 迁移学习

迁移学习(transfer learning)的基本思想是将从一个环境中学到的知识用于新环境中的学习任务。

目前，迁移学习已被广泛应用于各个领域，例如，在文档分类方面，Dai等[15]提出联合聚类的方法，通过不同领域共享相同的词特征进行知识迁移；在智能规划中，Zhuo等[16]提出一种新的迁移学习框架TRAMP，通过建立源领域与目标领域之间的结构映射来迁移知识，获取人工智能规划中的动作模型。

2 基于改进CNN的多标记分类算法

2.1 算法框架

由于图像传递信息的底层机制相通，因此可以利用迁移学习，将在源域上训练好的网络模型，通过共享网络参数，使之在目标域上也具有一定的特征提取能力。本文采用在ImageNet[17]数据集上训练好的Inception V3[18]模型进行图像特征提取。该模型引入了“Factorization into small convolutions”的思想，将一个较大的二维卷积核拆分成两个较小的一维卷积核，例如将 3 × 3 的卷积 核 分 解 成 1 × 3 和 3 × 1 两 个 卷 积 核。这 种 非 对称的拆分方式减少了网络参数量，降低了过拟合风险，可以保证对ImageNet之外的数据集具有很好的泛化性能。

为了进一步减少全连接层参数数量，本文对Inception V3模型的全连接层进行改进，引入双通道神经元，优化网络结构，并结合迁移学习提出了多标记分类模型ML_DCCNN。最后，将全连接层的输出送入SoftMax分类器，从而得到各标记的预测概率，然后根据各标记的概率计算多标记分类损失函数。

在反向传播时，保留Inception V3模型的特征提取层，即固定特征提取层的权重和偏置参数，并用神经元个数为20的全连接层替换原有全连接层，设置该层的初始权重和偏置为0，学习率设置为0.001，batchsize设置为100。然后，使用随机梯度下降算法，用PASCAL Visual Object Classes Challenge(VOC)数据集[19]对网络参数进行微调，使其适应于新数据集，算法的具体流程如图2所示。

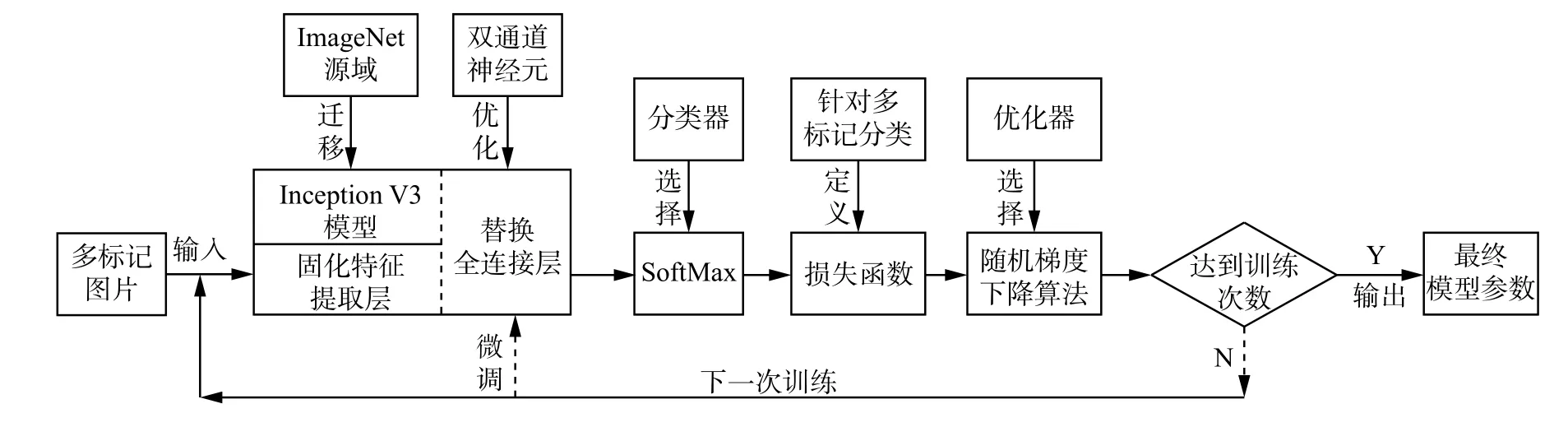
图 2 基于改进CNN的多标记分类算法框架Fig. 2 Multi-label classification algorithm framework based on improved convolution neural network

2.2 双通道神经元

在卷积神经网络中，卷积、池化和激活函数等操作将原始数据映射到隐层特征空间，全连接层则将学到的分布式特征表示映射到标记空间，即全连接层在整个卷积神经网络中起到了“分类器”的作用。但全连接层上往往包含大量参数，对整个网络的速度有一定影响。虽然FCN[20]全卷积模型取消了全连接层，避免了全连接层的副作用，但是在Zhang等[21]的研究中，全连接层能够在模型表示能力迁移过程中充当“防火墙”的作用，保证模型表示能力的迁移。因此为了能够在保留全连接层的基础上，减少网络参数，本文提出了双通道神经元的概念。

2.2.1 基本结构

本文将全连接层中只能接受一种标记特征信息的神经元称为普通神经元，如图3(a)所示，全连接层中最后一层的神经元个数和具体分类问题的标记总数相等，如某数据集上共有 n 种标记，则最后一层全连接层上的神经元个数为 n。

本文将可以接受两种标记特征信息的神经元称为双通道神经元。一个双通道神经元相当于两个普通神经元的合并，它改进了全连接层，有效地减少了该层的参数。在接受到特征信息后，为了能将合并的标记区分，使用双通道的神经元，需在其后再连接两个神经元，分别表示对应的标记，并规定所连接的两个神经元上的权重分别为1和-1，如图 3 (b)所示。

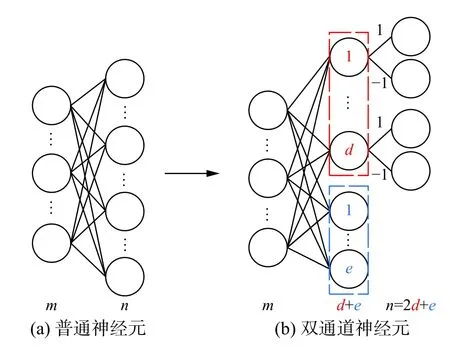
图 3 全连接层Fig. 3 Fully connected layer

在图3(a)中，假设分类标记数为 n，全连层输入为 m，则权重参数有 m ×n 个 ，偏置参数有 n 个，总 参 数 有 m × n+n 个。ception V3 模型的输入 m 为 2 048，输出标记 n 为20，所以在 m 远 大于 n 前提下，使用双通道神经元最多可缩减一半参数，如公式(1)所示：

式中： m ≫n； n =2d+e。

在图3(b)中，假设全连接层有 d 个双通道神经元和e个不使用双通道的神经元。在同样假设条件下，该层权重参数为 m × (d+e)+2d 个，偏置参数为d+e个，总参数为 ( m +1)×(d+e)+2d 个。一般情况下，输入值 m 远大于输出值 n，例如In-

2.2.2 核心思想

打包和解包是双通道神经元的核心思想。打包主要表现在将两种标记合二为一在一个神经元上，即最后一层全连接层上的每个神经元可以表示两种标记，接受两种标记的特征信息。例如：将飞机和自行车这两种标签打包在一起，由一个神经元负责输出，则该神经元上的权重只对飞机和自行车的特征信息敏感。但仅用一个神经元输出，存在无法判别输出是飞机还是自行车的情况，因此需要解包思想，主要表现在一个神经元又“分裂”出两个神经元，具体如图4所示。

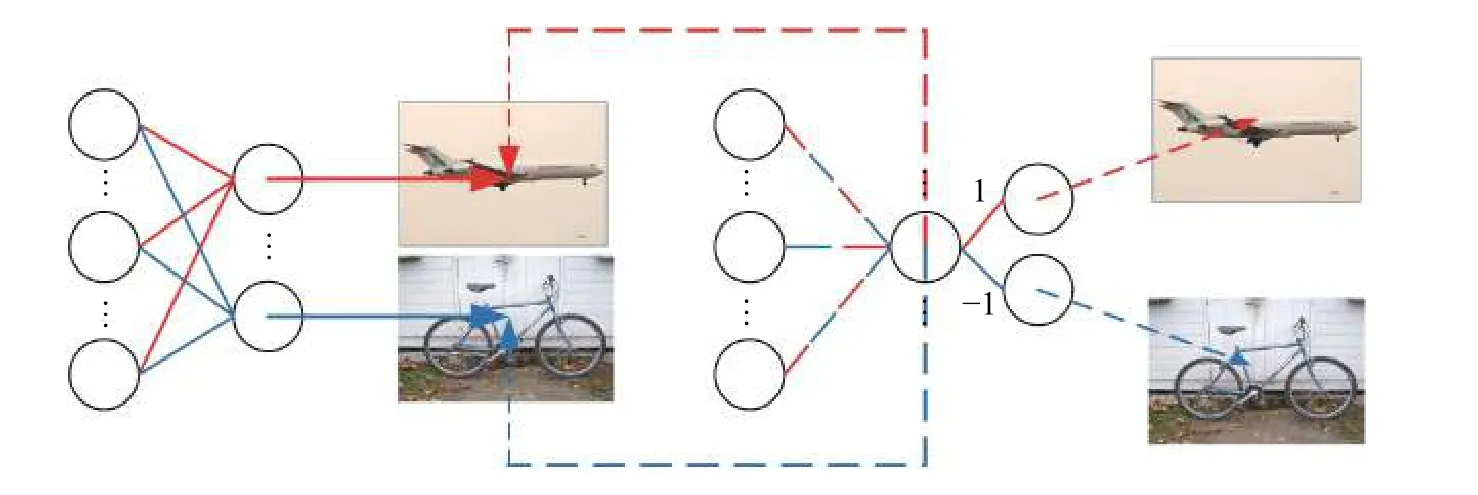
图 4 打包与解包示意Fig. 4 Package and unpack diagram

图4左边为普通全连接层的神经元，每个神经元仅对一种标记特征信息敏感，如上方神经元仅对飞机特征信息敏感，下方神经元仅对自行车特征信息敏感。图4右边使用了双通道神经元，每个神经元对两种类别的特征信息敏感，例如同时对飞机和自行车的特征信息敏感，在提取出飞机和自行车的特征后，再分裂出两个神经元分别代表对应的标记，其中权重为1的代表飞机，权重为-1的代表自行车。

2.3 损失函数

设 D ={(xi,yi)|i=1,2,···,n} 代 表具有 n 个样本的训练集，其中 xi=[xi1xi2···xid] 是 第 i 个 样本的d维特征向量， yi=[yi1yi2···yiq] 是 第 i 个样本的标记向量，其维度 q 与数据集标记总数相等， yij=1 表示xi含有标签 lj， yij=0 则表示不含有。

SoftMax分类器不仅可以用于处理单标记分类问题，也可以用于处理多标记分类问题。本文将最后一层全连接层的输出送入SoftMax分类器中，得出图片含有各标记的概率，例如图片xi含有标记 lj的概率：

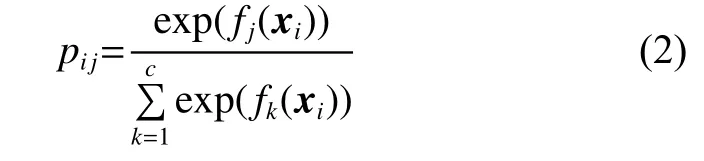
式中：fj(xi)表示图片xi对应标记 lj的 激活值，q表示数据集的标记总数。经过SoftMax分类器输出各标记概率后，定义交叉熵损失函数：

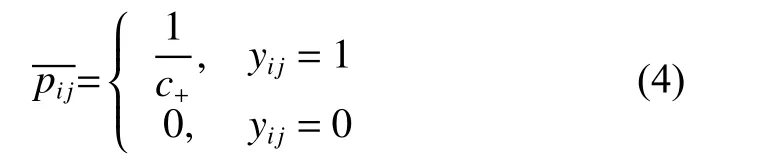
由式(3)和式(4)可以推导出：

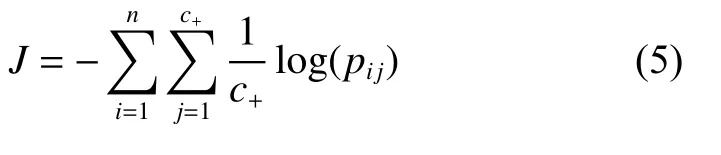
式中：n 表示一个Batch上的图片数量；c+表示图片xi上正标记的总个数。

3 实验与分析

本文实验在处理器为i5-3210M的Windows PC机上完成，基于TensorFlow 1.2.1实现卷积神经网络，采用了PASCAL VOC2007和PASCAL VOC2012两个多标记数据集，二者均含有20个类别标记。PASCAL VOC2007数据集共有9 963张图片，其中训练验证集有5 011张，测试集有4 952张，PASCAL VOC2012共有33 260张图片，其中训练验证集有17 125张，测试集有16 135张。

为了验证双通道神经元的可用性，本文对普通全连接层结构和采用双通道神经元的全连层结构的分类效果进行了比较，其中双通道神经元的标签两两合并方式如表1所示。表2显示了PASCAL VOC数据集中的一个多标记图像(如图5)分别使用普通全连接层和包含10个双通道神经元的全连层在训练2 000步时，softmax分类器的输出值，其中，FC表示普通全连接层，DC(Dual_Channel)表示双通道神经元全连接层，GT表示ground_truth。DC所用 d 值为10，即10个双通道神经元结构。表3为训练了5 000次的普通全连接层FC和使用10个双通道神经元的全连接层DC在100张图片上每个标记sof tmax的平均输出值，其中NUM表示在100张图片上每个标记出现的总数，出现次数最多的标记分别为person和car，可以看出两种全连接层在这两个标记上所对应的softmax也最大，且很接近。由表2和表3可知，在使用10个双通道神经元时，全连接层参数缩减了近一半，但网络仍能准确识别出多标记图片中的物体类别，且sof tmax分类器的输出值与普通全连接层相近，在一定程度上证明了双通道神经元的可用性。

图 5 多标记图像Fig. 5 Multi-label image

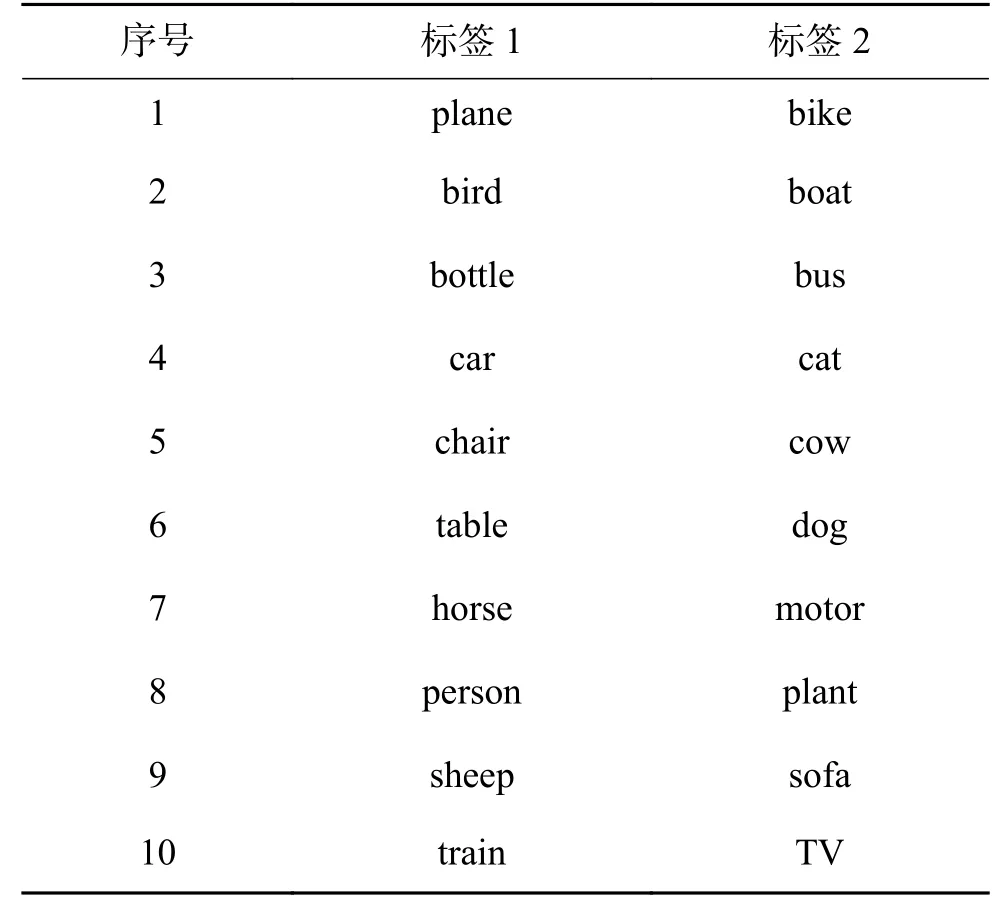
表 1 标签合并方式Table 1 Label merging mode

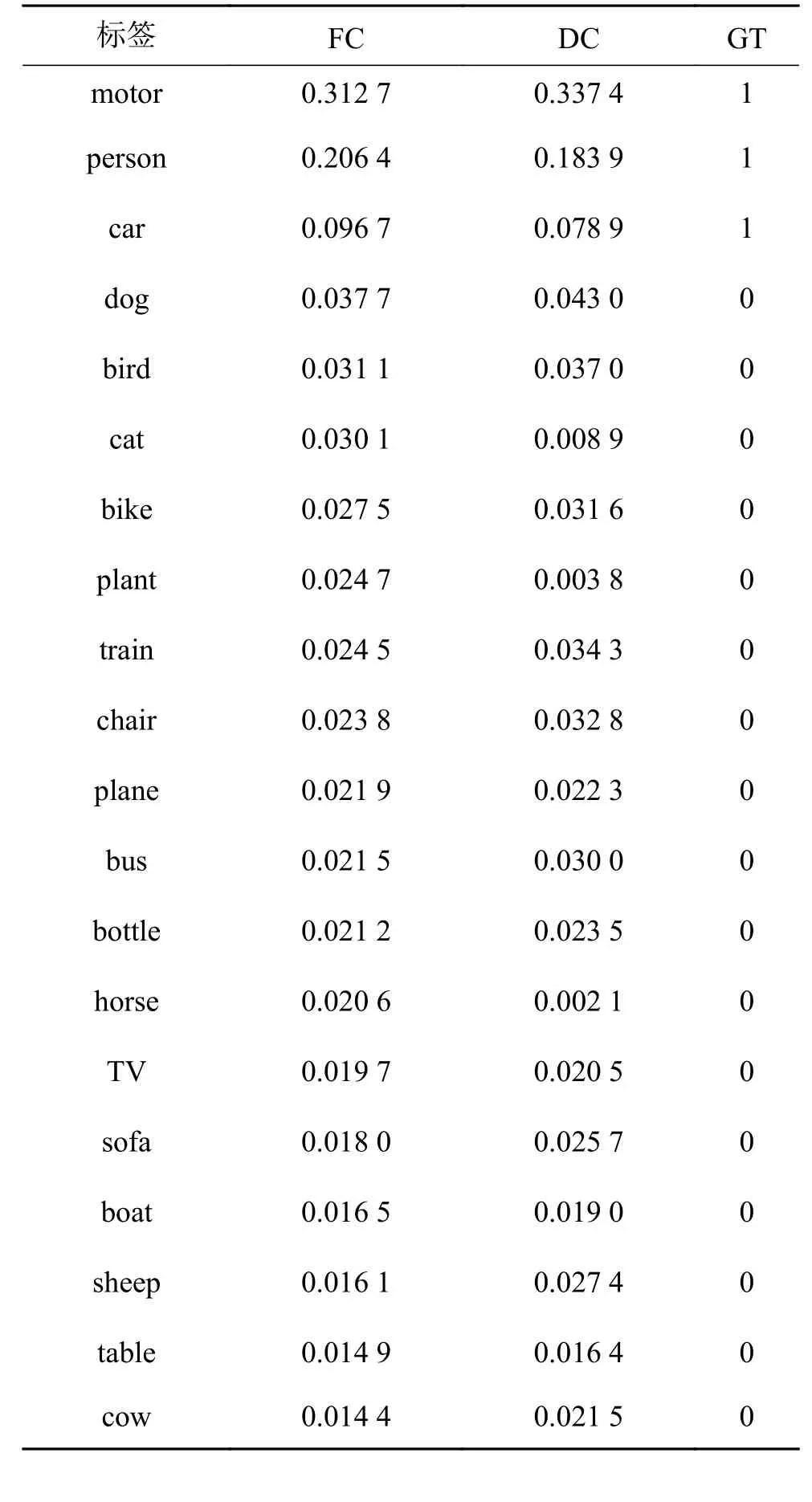
表 2 使用两种全连接层的分类结果比较Table 2 Result comparison of two fully connected layers

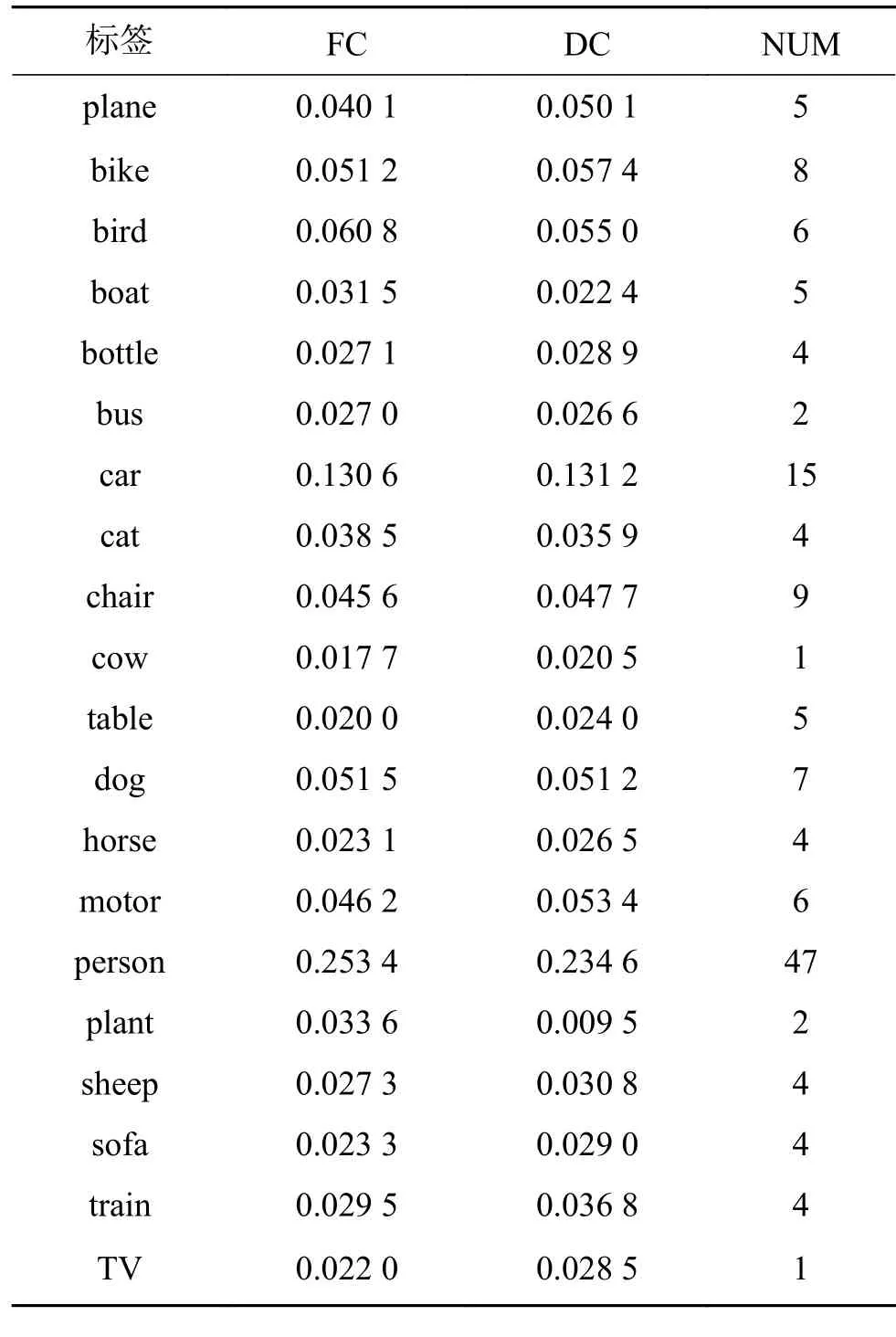
表 3 两种全连接层的平均分类效果比较Table 3 Average effect comparison of two fully connected layers

为了说明双通道神经元个数对分类效果的影响，在PASCAL VOC2007数据集上对比了双通道神经元个数 d 分别取不同值时的模型分类效果，如表4所示。由表3可见，随着 d 值增大，平均准确率(mean average precision, mAP)值在降低，每个标记所得最高AP值出现在非双通道神经元的输出中，即双通道神经元在减少参数的同时牺牲一定的准确率，变化趋势如图6所示。图6中，λ表示双通道神经元所占的比例， λ = d/n。由图可见，随着 λ 增大，mAP逐渐降低，当 λ = 0.5 时，mAP取最小值；实线表示全连接层上的参数缩减比例 β ， 随着 λ 增 加， β 逐 步上升，当 λ = 0.5 时，β达到最大值0.5。

为了验证ML_DCCNN模型的分类效果，本文分别在Pascal VOC2007和Pascal VOC2012数据集上进行实验，比较了ML_DCCNN、普通全连接层模型CNN-SoftMax、传统的多标记分类算法INRIA[22]、FV[23]和 G S-MKL[24]，以及基于卷积神经网络的多标记分类模型PRE-1000C[25]和HCP-1000[26]，评价指标使用 A ccuracy Precision(AP)，双通道神经元个数 d 取10，实验结果如表5和表6所示。由表可见，相对于传统算法的多标记分类算法，深度神经网络在图像特征提取和分类效果上有着明显优势，其中PRE-1000C和HCP-1000基于AlexNet卷积神经网络，相比于本文迁移学习所使用的Inception V3模型所得mAP值较低。

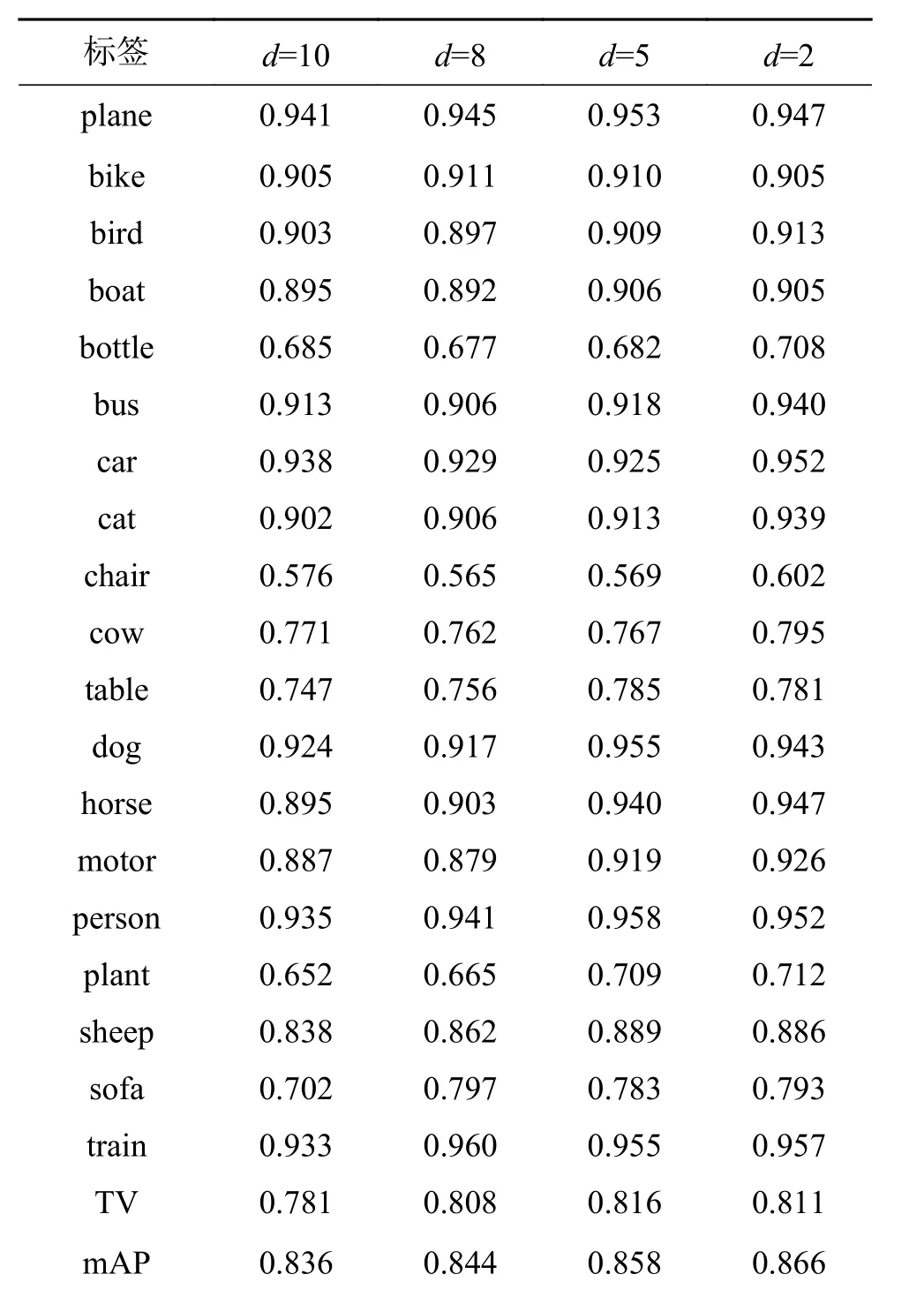
表 4 d取不同值时AP在PASCAL VOC2007数据集上的变化Table 4 Comp ar ison of AP of algor ithm on PASCAL VOC2007 data set

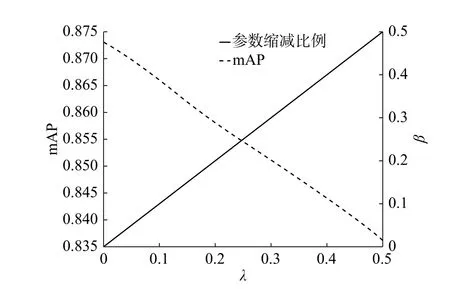
图 6 双通道神经元比例λ 对平均准确率mAP和参数缩减比例 β 的影响Fig. 6 Effect of dual-channel neuron ratio λon the mAP and ratio β of parameter reduction

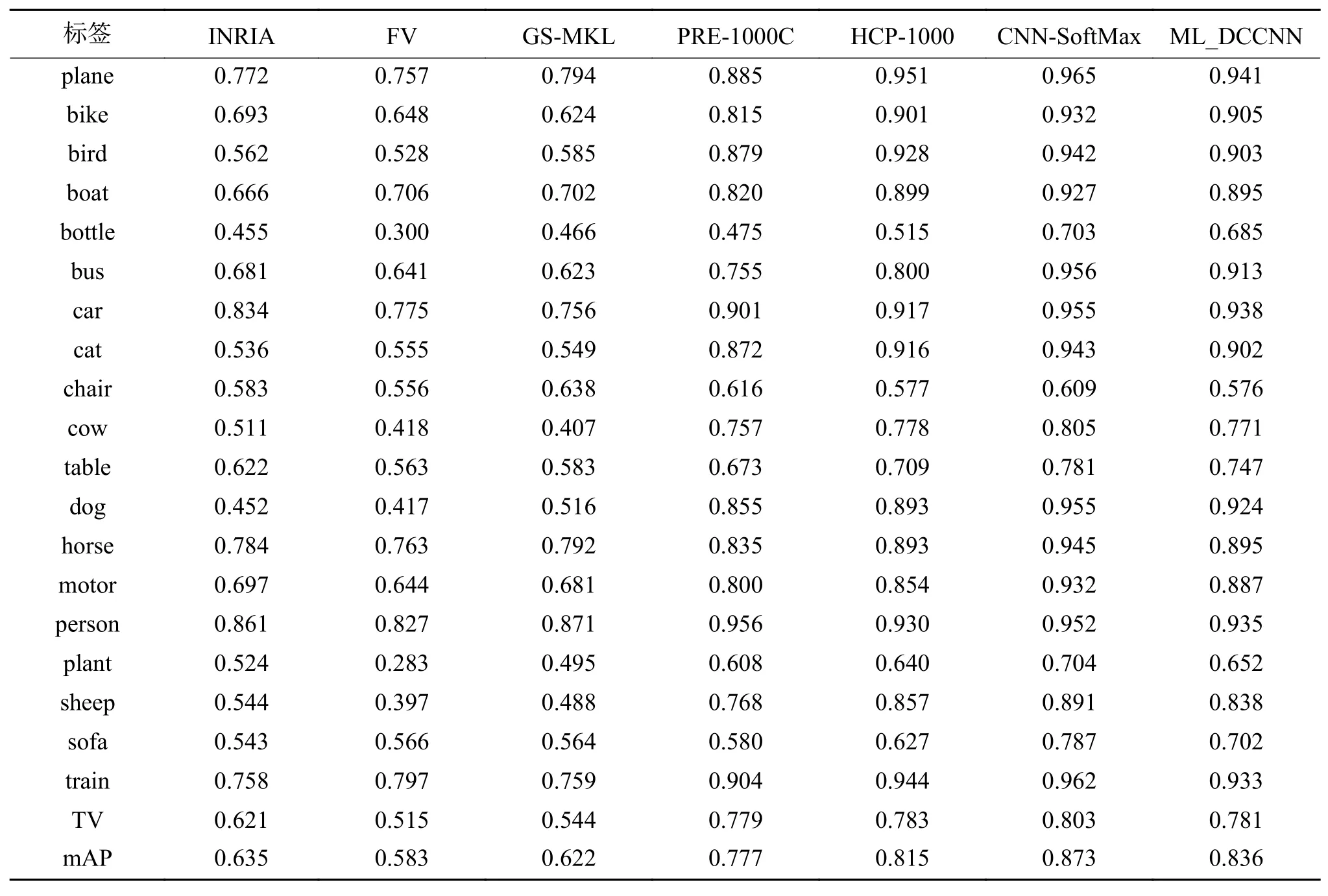
表 5 不同分类算法AP在PASCAL VOC2007 上的比较Table 5 Comparison of AP of different classification algorithms on PASCAL VOC2007 data set

表 6 不同分类算法AP在PASCAL VOC2012数据集上的比较Table 6 Comparison of AP of different classification algorithms on PASCAL VOC20012 data set

总之，通过实验可以证明使用双通道神经元能够对全连接层参数进行一定比例的缩减，而由于全连接层参数往往是迁移学习过程中所需要训练的全部参数，因此全连接层参数的缩减在一定程度上意味着整个网络模型的参数缩减。虽然双通道神经元在特征提取方面存在一定准确率损失，但整体性能依然在可接受范围之内，双通道神经元提供了不同程度的参数缩减与性能表现的可选择性，某种程度上增加了网络模型的灵活性。

4 结束语

本文提出了一种基于卷积神经网络的多标记分类方法，设定了针对多标记分类的损失函数，并在PASCAL VOC2007和PASCAL VOC2012两个多标记数据集上进行了验证。总体而言，与以往的方法相比，本文提出的使用迁移学习和双通道神经元多标记分类方法，可以在保证一定准确率的前提下减少网络参数，节省计算资源。在当下注重准确率和计算量平衡的背景下，有着较好的适应性和应用前景。但限于数据、机器性能等因素，本文没有进行更多的实验来证明标记相关性约束条件下分类算法的性能。因此将来的工作从以下方面开展：利用深度学习模型构建标记之间的依赖关系以及在标记依赖关系约束下进行多标记卷积神经网络的训练。