液力变矩器流动数值模拟的发展与应用
(吉林大学机械与航空航天工程学院, 吉林长春 130000)
引言
液力变矩器广泛应用于车辆、工程机械、起重运输机械、钻探设备的传动。液力变矩器主要由泵轮、涡轮和导轮组成,在工作过程中,液流与叶轮的相互作用,包括速度的变化、能量和转矩的变化与传递,是一个极其复杂的过程。液体在工作轮流道中的流动是黏性、不可压缩、不稳定的三维流动,其流动机理尚未完全被人们掌握[1-3]。
随着计算机技术和湍流理论的发展,计算流体动力学(Computational Fluid Dynamics,CFD)正逐渐成为流体力学研究的重要方法之一[4-5]。从1960年以来,CFD技术已经迅速发展成由计算机技术和数值计算组成的一门交叉学科。应用CFD计算可以对液力变矩器进行流场分析以及对传动性能进行准确预测,辅助液力变矩器叶片设计,依据内部流动信息调整结构参数,可以大大缩短变矩器研发时间且有针对性地改善机械性能,提高变矩器产品设计的成功率,有效降低开发成本。
1 湍流模型及其在液力变矩器CFD中的应用
多年来,液力传动研究者尝试将各种湍流模型用于液力变矩器的CFD分析。
RANS是目前工程应用最为广泛的湍流模型,它主要是基于对N-S方程中湍流脉动值的Reynolds应力项的假定——雷诺应力模型(Reynolds Stress Models,RSM)与涡黏模型[6]。
RSM是指针对雷诺应力张量的所有分量构造附加输运方程,然后联立求解时均化的RANS方程、新建立的附加输运方程及关于耗散率ε或比耗散率ω的附加尺度确定方程。
k-ε模型是指通过引入关于湍动能k和湍动耗散率ε的输运方程,并借助k和ε表征湍动黏度来实现雷诺时均模拟的两方程模型,是典型的涡黏模型。自标准k-ε模型出现以来,该模型就以模型简单、计算稳定性好、计算效率高而广泛应用于各种湍流模拟中。k-ω模型是在k-ε模型之后发展起来的另一类两方程涡黏模型。k-ω模型用比耗散率ω的方程代替了k-ε模型中的耗散率的方程。目前可供选择的k-ω模型主要有3种:Wilcoxk-ω模型、Baselinek-ω模型和SSTk-ω型。
但是RANS在实际应用中,存在两个重要的问题:当叶轮转速较大时,流场存在大量的流动分离区,计算精度会降低;当需要关注瞬态流场信息时,RANS不能满足要求[7],因此,尺度解析法(SRS)产生了。
SRS是指对一部分的流场信息进行直接求解,其余部分通过数学模型来计算,相比RANS,虽然计算效率降低了,但是能够求解流场的详细瞬时信息[8]。SRS主要分为大涡模拟(Large Eddy Simulation,LES)和RANS与LES优势混合的RANS/LES(HRL)模型。
LES的基本思想是先通过N-S方程进行空间滤波,利用瞬时的N-S方程直接模拟湍流中的大尺度涡,不直接模拟小尺度涡,而小涡对大涡的影响通过近似的Subgrid-scale (SGS)模型来考虑[9-13]。但是对于网格的要求更高一些,需要更加精细的网格、较小的时间步长和迭代次数,对计算机的性能要求更高一些。
由于LES计算量巨大,近年来有研究者提出最新的模型改善计算成本,不断提高计算效率,将RANS方法和LES方法相结合,提出了一系列的LES/RANS混合方法(HRL),很好的解决了LES计算成本高昂的问题,得到了工程领域的广泛应用。在HRL方法中,LES方法用来处理大规模分离流动,RANS方法用来处理近壁面边界层附近的湍流耗散和弱分离流动。因此HRL模型综合了RANS和LES的优点,从而突破了LES和RANS的先天局限性[14]。
表1为文献中研究者在液力变矩器CFD模拟过程中模拟方法的使用情况。
2 液力变矩器流动模拟方法的发展
2.1 网格划分
划分网格是流体计算必不可少的环节,网格的型式、数量以及一些加密处理等等对计算变矩器内部流场有着重要的影响。整个仿真过程中划分网格是最耗费时间的一个环节,通常可以按网格数据结构将网格分为结构网格和非结构网格。对于液力变矩器来说,叶片是工作轮传输流体动力最重要的部分,其边界层的湍流流场结构对于整个流场分析有着重要的影响,因此划分网格的时候一般会在此区域进行适当的加密处理。
最初,由于计算机硬件条件的限制,研究人员对液力变矩器进行数值模拟多采用单流道进行计算模拟,文献[16]、[35]、[36]都是只对液力变矩器单流道进行了数值模拟,如图1a~图1c。3个叶轮的内环、外环和叶片中间的空间,加上各叶轮之间的无叶片区构成了液力变矩器的工作流道。假设同一工况下,同一叶轮的每个流道的流场特性相同,那么就只需选取一个流道空间作为计算区域进行分析。这样进行单流道计算可以节省时间、对计算机的要求不高,但是由于单一流道模型存在很多假设,比如流道的周期性假设、内部流动的稳定性假设、液体不可压缩假设等,而变矩器的真实流动是不具周期性的,是随时变化且液体可压缩的瞬态流动过程,因此仅对单一流道进行模拟,不能得出液力变矩器各轮出口和进口的实际数据交换关系,模拟结果不十分准确。
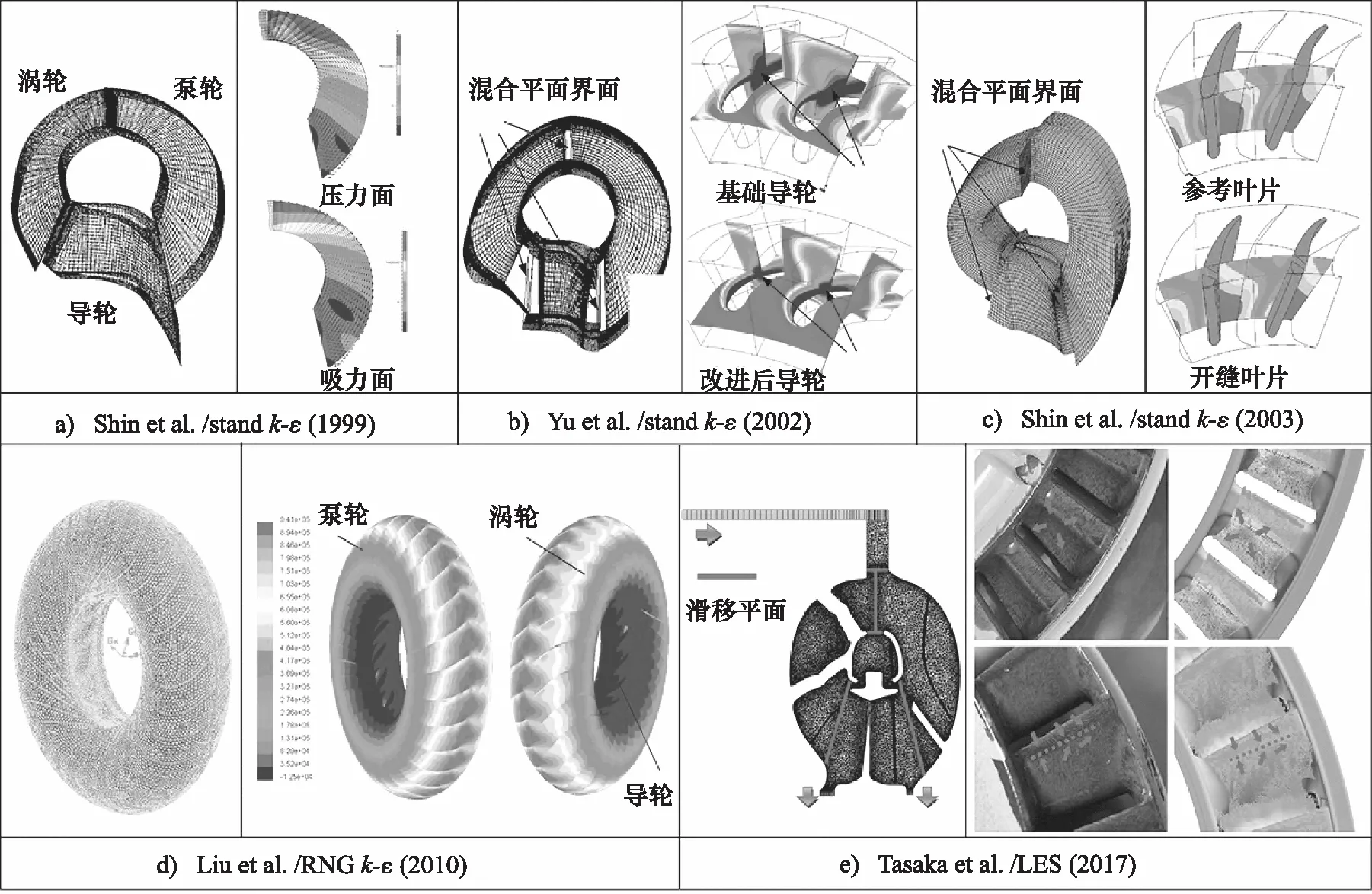
图1 液力变矩器单流道和全流道网格模型

表1 文献中数值模拟方法使用情况
随着计算机技术的发展以及仿真软件功能的完善,研究人员开始对液力变矩器进行全流道分析。文献[37]、[38]均对变矩器全流道模型进行了数值模拟,采用滑动网格法计算瞬态的变矩器三维湍流流动,如图1d、图1e,由图可以看出采用全流道网格可以更真实地反映瞬态流场的变化。
由此可见,液力变矩器的网格从单流道到多流道、从四面体网格到六面体网格,向着质量更高的结构化全流道网格发展。
2.2 多流动区域耦合算法
液力变矩器中各叶轮转速不同、叶片及流道形状复杂、动叶轮与静叶轮相互影响等因素造成其内部流动极其复杂,利用数值模拟进行研究是较为现实与经济的方法。随着多流动区域耦合算法的出现,使得液力元件内部流场整体模拟成为可能。
对于液力变矩器多流动区域耦合问题,一般有以下几种方法:多参考系法(MRF)、混合平面法、滑动网格法。多运动参考系法和混合平面法属于稳态算法,在计算过程中忽略了叶轮间相对运动产生的瞬态交互效应,而滑动网格法则属于瞬态算法,更适用于液力变矩器瞬态的模拟计算。
2.3 变矩器内流场仿真新方法-格子Boltzmann方法(LBM)
近年来,格子Boltzmann方法(LBM)已发展为一种模拟流体和物理问题的新颖的、有前景的数值方法。LBM是基于统计物理,并以极其简单的形式描述粒子的微观行为,但在宏观层次上正确反映流体的运动。由于它计算简单、本质并行和易于处理边界的优点,使得LBM在这几十年里,在许多领域的各种问题求解上取得很大成功。
文献[39]研究了基于LBM方法的液力变矩器导轮内流场数值计算理论与方法,发现LBM与传统CFD方法相比,计算数值比较接近,LBM可以获得十分详细的流场形成过程以及局部微小的流动细节,但是对计算资源要求更高一些。
3 液力变矩器内流场流动结构分析
如何用仿真得到的内部流场特征指导变矩器的优化设计一直是众多学者关注的问题。叶栅内二次流、气蚀等现象已经成为液力变矩器流场解析的重要课题。为了深入了解这些流动机理,各国研究人员将越来越重视对流场流动细节的把握。文献[40]采用多相流中的VOF模型在泵轮植入气泡,通过仿真结果总结出单气泡在流场中的流动轨迹和气泡破碎规律,揭示了气泡在传递过程中充当活化穴,释放过度热,引发气化现象,根据气泡湮灭发生原理,预测气蚀发生区,如图2a所示。文献[41]对不同速比下内部流场进行数值模拟,CFD数值仿真结果与试验值最高误差小于5%,并发现二次流主要出现在泵轮和导轮中,其中叶轮进出口处漩涡湍动能较高,能量损失较大,如图2b所示。文献[42]利用非定常计算方法对汽车用变矩器进行了三维数值仿真计算,发现泵轮的尾流对涡轮流场有着比较强烈的影响,如图2c所示。
在实际工程问题中,液力变矩器在工作过程中工作油温度会不可避免地上升,从而会产生温差,形成温度场。当温度变化的时候,工作油的物理属性也会随之变化,比如黏度会随温度升高而减小。而变矩器的外特性对于工作油的热物理属性是敏感的。传统的流场计算往往忽略工作介质的热物性,因此研究人员在能够准确预测液力变矩器流场的流动趋势之后开始考虑热流场。此外,将变黏度和恒黏度情况下的液力变矩器内部热流场结构进行对比分析,阐述了基于变黏度的SRS数值模拟提高液力变矩器外特性预测精度的原因,进而验证了考虑温度变化影响对变矩器进行SRS计算的必要性。文献[34]在数值模拟过程中考虑了温度变化对工作介热物理性质的影响,原始特性预测精度最大误差可以在3%以下,如图2d所示。
近年来,为了进一步提高液力变矩器的性能,有研究人员将仿生技术运用到叶片设计中,提出了仿生叶片,并用数值模拟进行了验证。文献[43]设计了仿鱼型泵轮和涡轮仿生叶片,经过CFD数值计算,变矩器最高效率相比普通叶片可以提高1.5%,如图2e所示。

图2 文献中对液力变矩器内流场的分析
4 基于数值模拟的液力变矩器外特性预测与集成优化
4.1 外特性预测
对于已有的变矩器来说,外特性曲线可以通过台架试验获得,但在变矩器设计过程中,不可能将设计模型全部做成样机并通过试验来获得其外特性。这样做设计周期长,且成本巨大。根据特性预测结果调整变矩器设计结构参数,以满足设计要求,不仅可以节约成本,减少变矩器设计周期,还可以有针对性地去改善变矩器某一性能。但是,对于变矩器外特性仿真模拟精度就有了较高要求。
大多数研究者采用稳态数值模拟或是RANS方法进行模拟,文献[15]对变矩器数值模拟得到的性能最大误差为15%;文献[17]采用Realizablek-ε模型对单流道进行模拟,最大计算误差为10%;文献[16]、[44]都对变矩器进行了三维数值仿真计算,通过外特性曲线算出最大误差为8%~10%;文献[22]得到的特性曲线与试验所得曲线基本一致,但是仍存在偏差,变矩比和能容最大偏差出现在低转速比区;文献[18]得到的最大误差为8%;文献[24]得到的最大误差为9%;文献[19]得到的最大误差为8%。由此可见,大部分研究者使用RANS模型进行液力变矩器数值模拟,其最大误差基本集中在8%~10%之间,甚至一些高达15%左右。
针对液力变矩器数值模拟中雷诺时均方法(RANS)预测精度较低且缺乏对流场结构准确描述的现状,文献[34]利用尺度解析模拟(Scale-resolving Simulation,SRS)方法实现其原始特性及内流场的模拟分析,结果表明,在典型工况下,SRS方法能够更好地捕捉到流动信息,具有较高的原始特性预测精度。尤其是SBES(Stress-blended Eddy Simulation)方法中的动态混合模型(Dynamic Hybrid RANS-LES,DHRL)得到原始特性预测结果的最大误差仅为3.24%,采用大涡模拟中的KET模型,预测液力变矩器特性的最大误差约为5%;采用IDDES、SAS与SBES模型的最大预测误差大致在3.5%~4%。
由此可见,尺度解析模拟方法对于变矩器外特性预测精度有明显优势。
4.2 集成优化
针对传统液力变矩器总体设计方法的缺点,近年来美国等发达国家的学者提出了一种新的设计方法多学科设计优化(Multidisciplinary Design Optimization,MDO)。其主要思想是在复杂系统设计的整个过程中,集成各个学科的知识,并充分考虑各门学科之间的相互影响和耦合作用,应用有效的设计、优化策略和分布式计算机网络系统,来组织和管理整个系统的设计过程,通过充分利用各个学科之间的相互作用所产生的协同效应,以获得系统的整体最优解[45-46]。液力变矩器优化设计流程如图3所示。

图3 液力元件优化设计流程图
很多研究者开展了MDO的理论和研究工作,并将其运用于一些简单系统设计中。文献[47]以最高效率、起动变矩比和最大泵轮扭矩系数为目标建立了多目标优化模型。利用MATLAB与Isight的集成优化对变矩器的性能进行了优化。文献[48]基于Isight集成软件平台将混合流道的模型集成为变矩器混合流道集成仿真平台,对涡轮输出轴按照设定的程序进行平稳加在、平稳卸载、急剧加载、急剧卸载工况下的性能仿真。文献[49]基于Isight进行了仿生沟槽非线性优化,进行了拉丁超立方设计、代理模型、非线性优化过程,从而确定减阻效果最佳的仿生叶片结构。
5 结论
通过对网格划分、计算模型、流场分析、集成优化四个方面研究现状进行分析,提出了液力变矩器数值模拟方面研究的几个趋势:
(1) 网格划分精细化 随着湍流模型的不断发展,对于流道网格的要求也越来越高。网格向高质量全流道结构化网格发展,结合边界层加密处理、滑移网格技术,进行CFD计算,如何将网格划分变得更高效率、更高质量是变矩器数值模拟研究方向之一;
(2) 湍流模型的发展 液力变矩器的流场数值模拟向更高效、更细致的方向发展,类似SAS和DES的组合模型,既能够捕捉更加细小的湍流涡,又有较高的计算效率;
(3) 流场预测精度更高 运用尺度解析模拟法求解液力变矩器瞬态流场,理论上比全模化的RANS方法更先进。用SBES法得到的预测精度与最大实验误差可以达到4%以下;
(4) 考虑热物性的液力变矩器热流场求解 工作油的热物理性质影响着变矩器的原始特性,而传统的流场计算往往忽略工作介质热物性,考虑温度对流场结构影响的热流场,可以实现变矩器外特性的高精度预测,对于热流场的研究也是变矩器研究的主要方向之一;
(5) 从介观角度对液力变矩器进行流场分析 格子Boltzmann方法是从介观角度对液力变矩器进行流场分析的方法之一,与传统CFD方法相比,LBM方法能够揭示更多的流场局部细节;
(6) 基于Isight的液力变矩器多目标优化 目前国内MDO技术在液力元件设计领域应用还较少,但是其通过实现各学科模块化并行设计来缩短设计周期,通过各学科综合考虑来提高可靠性、降低研制费用等优点决定了MDO技术必将成为液力元件优化设计的大趋势。
——变矩器的锁止控制

