流-固多层结构中软层介质参数反演研究

黄建伟，韩庆邦，仲晓敏，蒋 謇

(河海大学物联网学院，江苏 常州 213022)

0 引 言

流-固界面波是指在流体与固体的交界面上传播的一种表面波，具有能量大、衰减小、传播距离远且容易监测和接收等优点。

SCHOLTE于1924年提出了流-固界面波的相关理论[1]，研究流-固界面波的传播特性。经过不断的研究与发展，流-固界面波理论已应用到了诸多领域，如具有粘滞特性的复杂流体、含多孔介质的固体、不平滑界面等[2]。近年来，流-固界面波开始被应用到海洋地质勘探及井孔探测等领域[3]。OHTA K等[4]利用电磁诱导在深度为一百多米的海洋底部激发出流-固界面波，然后利用地声侧听器采集信号，通过遗传算法反演出了海底的剪切波速；WILKEN D等[5]采集地震数据并分析反演概念，凭借粒子群优化算法对采集到的信号进行成像，进而分析得出了海底的特征参数；宁汇勇等[6]依据地层与井中流体交界面上的流-固界面波，沿井壁采集波形信号，经过数据处理后得到井层的渗透率及储层划分。

在大坝中存在大量流体与固体的交界面，在交界面上存在流-固界面波。大坝在长期的使用中可能会出现裂缝、空洞等缺陷，缺陷的存在可能会引发大坝事故。由于大坝特殊的原理及构造，一旦大坝出现事故，将会造成非常严重的后果。因此经常对大坝进行监测，及时发现大坝的异常，对大坝进行维护，十分重要。

缺陷会使缺陷层的横波波速减小，使混凝土变“软”，因此可以使用软层介质来表示出现缺陷的地方，缺陷的大小反映在软层介质的深度、厚度及横波波速上。缺陷可能会对流-固界面波的传播特性产生影响，因此我们来研究缺陷会对流-固界面波的传播特性产生怎样的影响，期望找到一种检测大坝缺陷的方法。

本文建立含有软层介质的流-固界面模型，推导了含有软层介质的流-固界面波的频散方程。根据频散方程计算频散曲线，改变软层介质的深度、厚度及横波波速参数，观察频散曲线的变化，探究软层介质的改变对频散曲线有怎样的影响。使用有限元软件建立仿真模型，使用遗传反向传播(Back Propagation,BP)神经网络，对模型参数进行反演，进而确定缺陷的位置及大小。

1 频散方程的建立

固体层内含有软层介质的流-固界面模型如图1所示。0＜z＜H1处表示流体层，z=H1处表示流体层与固体层的交界面(流-固界面)。z＞H3处表示半无限固体层，流-固界面波就是指在z=H1界面上传播的波。

图1 含有软层介质的流-固界面模型Fig.1 The fluid-solid interface model containing a soft medium layer

文献[7]中提到，Ben-Menahem于1965年引入了B，P，C坐标系，引入使用位移和应力表示的矢量Smn及势矢量φmn，如式(1)所示，这里m的取值为m=1,2,3,4，表示图1中从上到下的介质层数，n的取值为n=1,2，n=1表示上界面，n=2表示下界面，为了方便表达，有时会省略下标。

式中，µB,µP,τB,τP分别表示沿B，P方向的位移及应力，ϕ+,ψ+和ϕ-,ψ-分别表示沿+z方向传播的下行波和沿-z方向传播的上行波。

在各层介质中，有Sm2=PmSm1，其中称为传递矩阵。

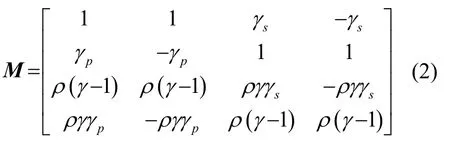
在流体层不存在横波，第4层半无限介质内不存在上行波[8]，则有即令则

式中，Gmn代表矩阵G的第m行、第n列，方程组有解的充要条件是其系数行列式为零，所以有

式(4)即为本文流-固界面的频散方程。

2 频散特性及分析

将各物理参数取值带入频散方程，经过计算便可得到频散曲线。各层物理参数取值如表1及表2所示。

表1 流-固界面模型的各层参数取值(第一种情况)Table 1 The parameter values of different layers in the fluid-solid interface model (the first case)

表2 流-固界面模型的各层参数取值(第二种情况)Table 2 The parameter values of different layers in the fluid-solid interface model (the second case)

当固体层内存在软层介质时，流-固界面波的频散曲线如图2所示，各层介质的厚度参数对应于表1中的①。

由图2可知，当固体层内存在软层介质时，流-固界面波的频散曲线具有多模态特征，基阶频散起始于10 kHz，在1 750 m·s-1处趋于无穷大，在60～70 kHz范围内趋于水平，在截止前表现为先降低后升高的趋势。

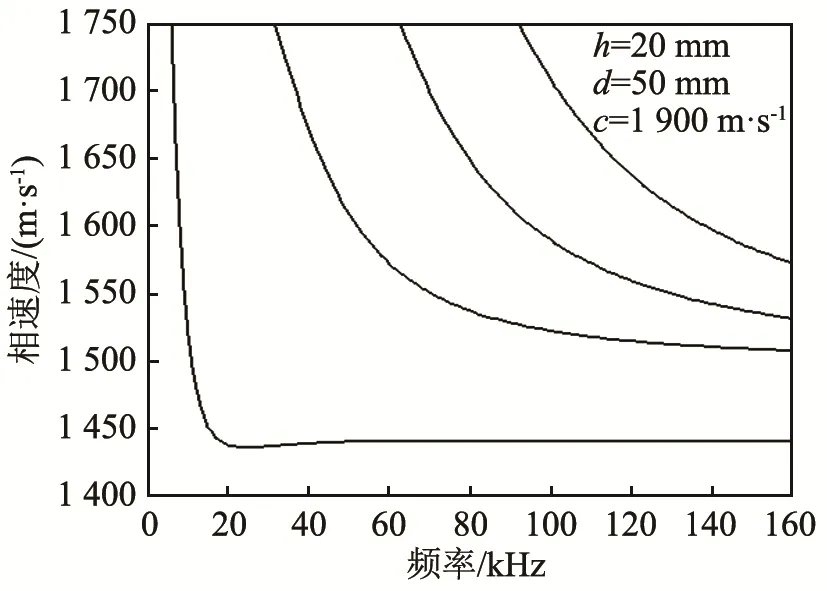
图2 固体层内存在深度h为20 mm、厚度d为50 mm、横波波速c为1 900 m·s-1的软层介质时流-固界面波的频散曲线Fig.2 Dispersion curves of fluid-solid interface wave for the soft medium layer parameters of depth h=20 mm,thickness d=50 mm and transverse wave velocity c=1900 m·s-1

改变软层介质的深度，观察频散曲线的变化，得到的结果如图3所示，各层介质的厚度参数对应于表1中的①和②。

图3 软层介质深度h不同时的频散曲线对比：实线表示h=20 mm，点线表示h=10 mm，其他软层介质参数为：d=50 mm和c=1 900 m·s-1Fig.3 Comparison between dispersion curves for the soft medium layer parameter h=20 mm (solid line)and h=10 mm (dotted line),other parameters are d=50 mm and c=1 900 m·s-1

由图3可知，当软层介质的深度减小时，基阶频散曲线趋于水平处的频率增大，且在趋于水平前先降低后升高，最小值减小。

改变软层介质的厚度，观察频散曲线的变化，得到的结果如图4所示，各层介质的厚度参数对应于表1中的①和③。

由图4可知，当软层介质的厚度减小时，基阶频散的起始频率增大，趋于水平处的频率减小，处于40～50 kHz范围内。

改变软层介质的横波波速，观察频散曲线的变化，得到的结果如图5所示，各层介质的厚度参数对应于表1中的①和及表2。

图4 软层介质厚度d不同时的频散曲线对比：实线表示d=50 mm，点线表示d=10 mm，其他软层介质参数为：h=20 mm和c=1 900 m·s-1Fig.3 Comparison between dispersion curves for the soft medium layer parameter d=50 mm (solid line)and d=10 mm (dotted line),other parameters are h=20 mm and c=1 900 m·s-1

图5 软层介质横波波速c不同时的频散曲线对比：实线表示c=1 900 m·s-1，点线表示c=1800 m·s-1，其他软层介质参数为：h=20 mm和d=50 mmFig.5 Comparison between dispersion curves for the soft medium layer parameter c=1 900 m·s-1 (solid line)and c=1 800 m·s-1(dotted line),other parameters are h=20 mm and d=50 mm

由图5可知，当软层介质的横波波速减小时，基阶频散曲线趋于水平处的频率减小，在趋于水平前先降低后升高，降低的速度变大，最小值减小。

软层介质对流-固界面波频散曲线的影响集中在基阶频散，因此可以根据频散曲线来反演软层介质的深度、厚度及横波波速。

3 遗传BP神经网络

遗传算法优化BP神经网络的流程如下[9]：

(1)将权值、阈值进行二进制编码；

(2)计算误差函数，使用误差函数的平方和的倒数作为遗传算法的适应度评价指标；

(3)使用遗传算法确定最优化权值、阈值；将最优化权值、阈值代入到BP神经网络，作为初始权值、阈值对BP神经网络进行训练。

根据频散方程，对各物理量赋予不同的值，即可达到大量输入样本。根据软介质的性质，取深度的范围为1～150 mm，厚度范围为1～150 mm，横波波速范围为1 700～1 980 m·s-1。使用基阶频散作为输入样本，样本间距设置为100 Hz，使用软层介质的深度、厚度和横波波速参数作为输出样本，对BP神经网络进行训练学习。

遗传BP神经网络训练完毕后就能够用来进行软层介质参数的反演，具体过程如图6所示。

图6 遗传BP神经网络反演软层介质的参数过程Fig.6 The process of inversing the parameters of soft medium layer by the genetic BP neural network

采用基阶频散数据进行反演性能测试，测试结果如图7所示。

图7 反演模型性能测试Fig.7 Performance tests of inversion model

通过测试样本反演得到的软层介质的深度h、厚度d、横波波速c的相对误差在0～10%之间。

4 仿真实验及结果分析

使用Comsol multiphysics软件对文中的流-固界面模型进行仿真。流-固界面有限元仿真模型如图8所示。第一层介质为水，第二层介质为理想混凝土，第三层介质为软层混凝土，第四层介质为半无限理想混凝土。软层介质的深度h、厚度d及横波波速c参数取值如表3所示。在流-固界面上采样点设置范围为20～50 cm，采样间隔为1 cm，如图8所示。

图8 流-固界面有限元仿真模型Fig.8 The fluid-solid interface model built by finite element software

表3 仿真模型中软层介质的参数取值Table 3 The parameters of soft medium layer in the simulation model

根据表3所示的参数，在距离激发源30 cm处获得的典型信号波形如图9所示。

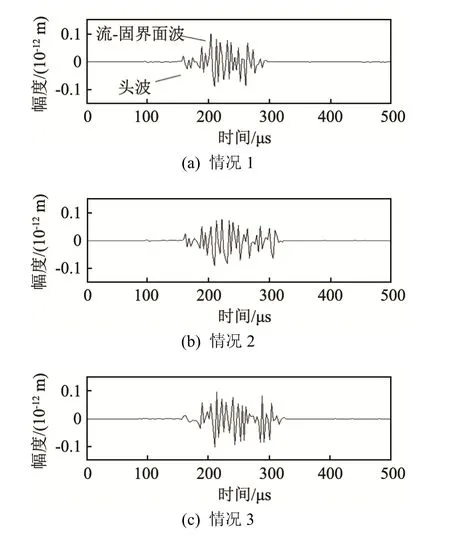
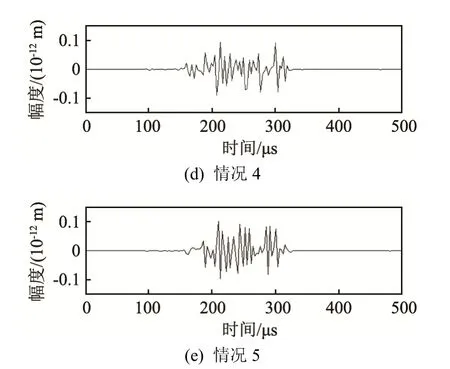
图9 各种情况下30 cm处的时域信号波形Fig.9 Time-domain signals at the receiving distance of 30 cm under the conditions shown in Table 3

由时域信号波形可知，对于30 cm处的观测点，头波首先到达，流-固界面波其后到达，且流-固界面波的频散具有多模态特性。利用各采样点采集到的时域信号，采用二维傅里叶变换法，二维傅里叶变换的具体表达式如式(5)所示，式中u(z,t)为采集的时域信号。

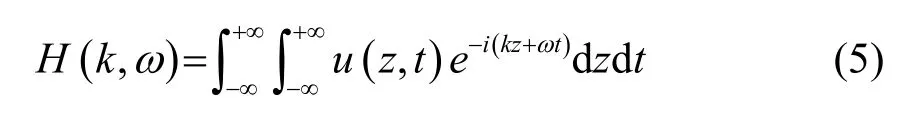
求得的频散能量谱的灰度图及频散数据如图10所示，由于软介质的影响大多集中于基阶频散，且高阶频散识别度较低，这里只取基阶频散。

使用求得的流-固界面波的基阶频散数据作为输入样本，样本间隔设为100 Hz，使用第3节中训练的遗传BP神经网络对软层介质的深度h、厚度d和横波波速c进行反演，结果如表4和表5所示。

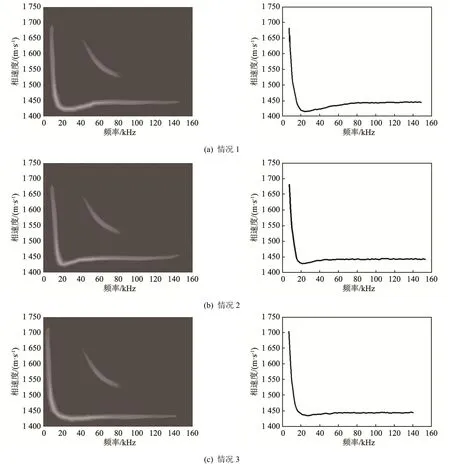
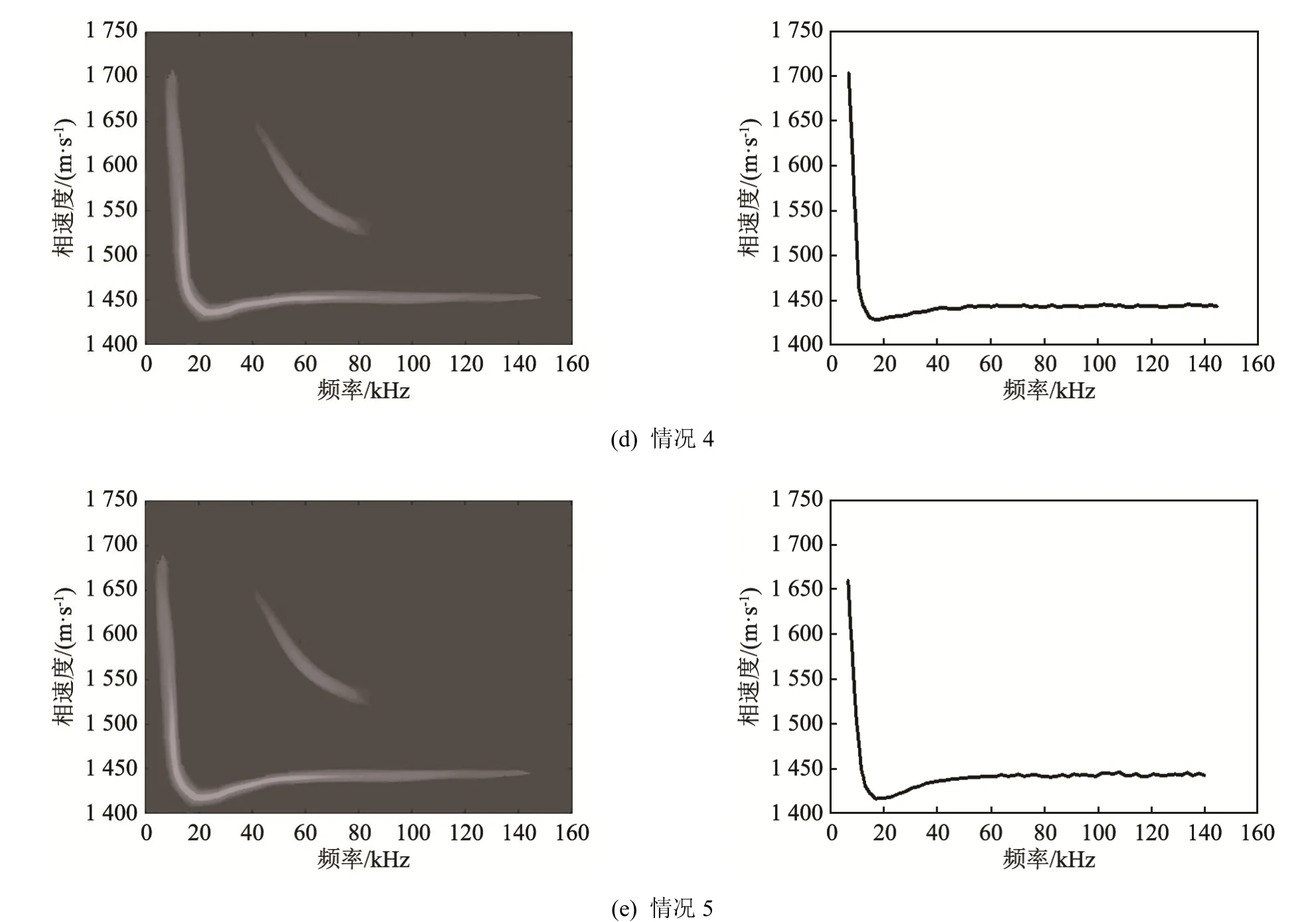
图10 各情况下的频散能量谱的灰度图及频散曲线Fig.10 Grayscale images of dispersion energy spectrum and dispersion curves in different cases

表4 遗传BP神经网络反演软层介质参数值Table 4 The inversion parameter values of soft medium layer in the genetic BP neural network

表5 遗传BP神经网络反演软层介质参数相对误差Table 5 The inversion relative errors of parameters of soft medium layer in the genetic BP neural network

由表5可见，反演得到的软层介质的深度、厚度及横波波速的误差在10%以内，处于较为理想的范围。造成误差的原因是多方面的，包括BP神经网络自身的误差，采集时域信号时的误差，利用时域信号计算频散数据时算法的误差等。

5 结 语

本文建立含软层介质的流-固界面模型，利用传递矩阵，推导了含软层介质的流-固界面波的频散方程。根据频散方程计算频散曲线，改变软层介质的深度、厚度及横波波速参数，观察频散曲线的变化。结果表明，当固体层内存在软层介质时，流-固界面波的频散曲线具有多模态特征，基阶频散在一定范围内截止，在截止前先降低后升高；当软层介质的深度减小时，基阶频散的截止频率增大，且截止前先降低后升高，最小值减小；当软层介质的厚度减小时，基阶频散的起始频率减小，截止频率减小；当软层介质的横波波速减小时，基阶频散的截止频率减小，截止前先降低后升高，降低的速度变大，最小值减小。

使用有限元软件建立仿真模型，使用遗传BP神经网络，对模型参数进行反演，反演结果在比较理想的范围内。反演结果表明，使用遗传BP神经网络，能有效地反演出软层介质的深度、厚度与横波波速参数。该结论为以后利用遗传BP神经网络，使用界面波方法反演大坝坝体内缺陷的参数提供了理论依据。