基于最小二乘和泰勒展开的超宽带无人运输车定位算法研究
高 培, 蒋学程, 何栋炜
(1.福建商学院信息工程系,福建 福州350012;2.闽江学院物理学与电子信息工程系,福建 福州 350108;3.福建工程学院信息科学与工程学院, 福建 福州 350118)
0 引言
目前的工业环境中大量使用无人运输车(automated guided vehicle, AGV),特别是智能仓储:多台AGV组成一个柔性的库内自动搬运系统,可以实现出入库货物和零部件的搬运工作。在障碍物较多的室内环境中,超宽带(ultra wide-band,UWB)由于具有高速率、高精度和低功耗等特点常用来对AGV进行无线定位[1]。主要原理是利用UWB信号测量AGV与定位基站之间的距离,测距完成后再利用定位算法得到AGV当前的位置。
目前常用的基于测距的定位算法有质心算法[2]、最小二乘算法[3]、Chan算法[4]、泰勒展开算法[5]以及利用多种算法进行协同定位[6]。质心算法以定位节点通信范围内的所有参考节点几何质心作为其估算位置,准确度较低[7],最小二乘算法求解非线性方程求出的并不是最优解,而是次优解,而Chan算法在非视距误差大量存在的环境下定位精度不高。UWB定位方程式是一个非线性方程组,泰勒展开算法是求解非线性方程的有效方法,由于其求解精度高、收敛速度快,比较适合于非线性方程组的求解,主要原理是根据初始值迭代求解出目标节点的最优解。文献[8]利用总体最小二乘确定泰勒迭代算法的初始值,而文献[9]通过阈值筛选和权重计算确定泰勒迭代算法的初始值,上述方法都是通过改善泰勒级数初始值来减少迭代次数,提高定位精度,但并不能消除测距误差对定位结果的直接影响,改善效果不明显。文献[10]提出一种基于UWB与惯性导航的复合定位方法,使用扩展卡尔曼滤波算法对UWB定位结果与惯性传感器数据进行融合,提高了动态情况下的定位精度,但系统硬件复杂度及成本较高。
在遮挡物较多的非视距室内环境中,当环境中存在金属、液体等对高频信号衰减影响很大的物体时,测距结果会出现较大误差[11],通过分析室内定位误差的来源,本文提出了一种改进的最小二乘和泰勒级数展开的定位算法,通过一种评价函数方法进行误差判断及参考节点筛选,筛除测距误差较大和离AGV较近的基站数据,再对筛选后的测距数据使用最小二乘和泰勒展开的定位算法得到目标节点的最优估计位置。
1 定位原理与算法描述
1.1 定位监测方案
AGV工作的仓储环境中参考基站一般是均匀分布在仓库中,如图1所示:UWB室内定位系统包括3部分:由带有定位传感器(sensor)的参考基站、自带电源和UWB定位标签(tag)的AGV、以及能进行数据监控和处理的定位平台组成。
AGV上的UWB定位标签产生脉冲信号并通过标签中的超宽带发射天线将脉冲信号辐射出去,架设在仓库中的参考基站接收到标签发出的脉冲信号,记录信号到达时间及发送时间,根据信号到达时间可以得到AGV与各参考基站的距离。AGV上的定位标签与参考基站通信机制如图2所示,采用基于到达时间的TOA(time of arrival)测距算法可以得到AGV到各参考基站的距离[12-13]:
di=c(T6-T3)-(T5-T4)+(T4-T1)-(T3-T2)/4, (1)
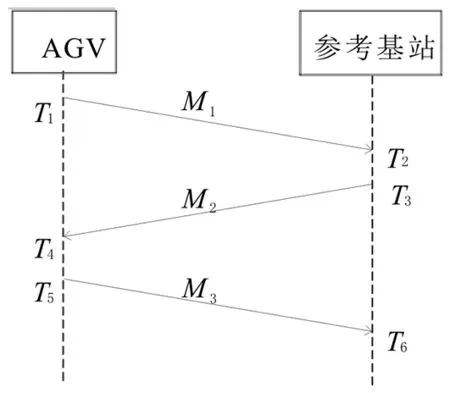
图2 AGV与参考基站的通信机制图Fig.2 Communication mechanism diagramof AGV and station
其中c=3×108m/s为信号传播速度,两点间的距离可由信号传播速度乘以信号传播时间求得,该计算方式不需要AGV上的UWB定位标签与参考基站上的定位传感器时钟同步,大大减少了硬件的复杂程度。
1.2 最小二乘和泰勒展开定位算法
在智能仓储环境中,假设n个参考基站坐标分别为(x1,y1),(x2,y2),…,(xn,yn),AGV的真实坐标为(xR,yR),AGV与n个参考基站之间的真实距离分别为r1,r2,…,rn,根据已知条件,可以得到定位方程组如下[14]:
(2)
在不存在任何误差的情况下,可以求解出真实坐标值(xR,yR)。
实际环境中AGV根据预知的参考基站的地址信息,分别向n个参考基站发起测距,测得AGV与n个参考基站之间的距离分别为d1,d2,…dn,测距时由于存在视距(line of sight,LOS)和非视距(not line of sight,NLOS)误差,实际测出的距离di=ri+λi,式中λi为AGV与第i个参考基站之间的测距误差。则方程应该写为:
(3)
因此,方程一般无解,即无法求得目标节点真实坐标(xR,yR),只能求得接近真实坐标的最优解(xD,yD)。若(xD,yD)为解出的目标节点的最优解,求解一般采用最小二乘方法,通过迭代计算,首先假设迭代过程中估计位置初始坐标为(xD0,yD0),初值(xD0,yD0)的计算见2.2节内容,目标节点真实坐标(xR,yR)与估计的初始位置(xD0,yD0)存在以下关系:
(4)
则方程可以改写为:
(5)
记:
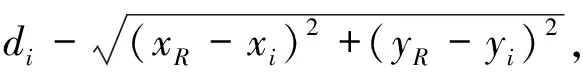
其中i=1,2,…n,由泰勒展开得:
(7)
忽略o(ρ),则:
(8)
记:
(9)
则由式(8)可得:
(10)
其中:
定义评价函数:
(11)
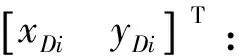
Ni=Ni-1+Δi。 (12)
迭代终止条件选择Δx+Δy≤ε,ε为事先设置好的阈值,此时求出的最优解(xDi,yDi)即为目标节点的最优解(xD,yD)。
2 改进的定位算法
2.1 方法提出
由于UWB硬件电路延迟及时间分辨率有限,结合TOA的测距理论可知AGV与基站位置越近,测距结果di的相对误差越大[15]。另外由于室内仓储环境中障碍物较多,比如其它AGV的移动、人员经过或者仓库中物品阻隔等,会使得AGV与某个参考基站的测距误差突然偏大,即使采用多次测距取平均值的方法,考虑到AGV如果在移动,多次测距间隔时间必须很短,也无法避免因障碍物造成对应方向上基站的干扰误差。
根据对最小二乘和泰勒展开定位算法及室内测距误差来源进行分析,可知测距误差会影响定位精度,要提高AGV的定位精度,需要对误差较大的测距数据进行处理。考虑定位算法受到测距误差影响,设计一种基于测距误差判断和筛选的方法,通过筛选排除误差较大的测距数据后再使用最小二乘和泰勒展开定位算法求出目标节点的位置,在改善定位精度的同时也能减少计算量。方法流程如下:
步骤1:通过最小二乘和泰勒展开的定位算法得到目标节点的初定位结果;
步骤2:利用初定位结果根据所设计的评价函数方法进行参考节点筛选;
步骤3:对筛选得到的定位数据再次使用最小二乘和泰勒展开定位算法得到最终定位结果。
2.2 初始值确定
步骤1中通过最小二乘和泰勒展开的定位算法求解初定位结果要求有初始值,初始值采用简单的三点定位方法计算得到,因对其精度要求不高,不考虑测距误差对它的影响。
任意选取的3个参考基站,坐标分别为(x1,y1)、(x2,y2)、(x3,y3),假设测量出3个参考基站与AGV的距离分别为d1,d2,d3,初始值坐标为xD0,yD0,由毕达哥拉斯定理可得:
(13)
使用最小二乘法求出xD0,yD0,即:
(14)
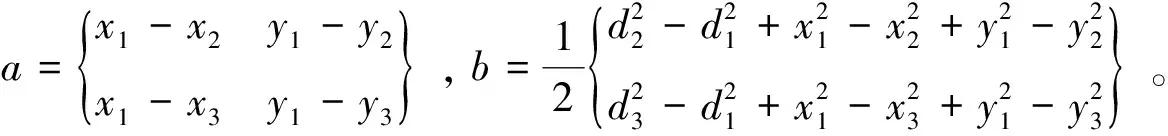
2.3 参考节点筛选
如图1所示的智能仓储环境中,已知参考节点坐标分别为(x1,y1),(x2,y2),…,(xn,yn),AGV根据参考基站的地址信息,向n个参考基站发起测距,测得AGV与n个参考基站之间的距离分别为d1,d2,…,dn,通过1.2节的最小二乘和泰勒展开定位算法可以计算得到目标节点的初定位结果(xD,yD)。
设节点(xD,yD)到n个参考节点的计算距离为d1m,d2m,…,dnm,则存在:
(15)
其中i=1,2,…,n,设Δdi为目标节点(xD,yD)到参考节点(xi,yi)测距di和计算距离dim的差,则存在:
(16)
记Δdi=di-dim,i=1,2,…,n。
若测量的距离d1,d2,…,dn没有任何误差,即存在d1=d1m,d2=d2m,…,dn=dnm,但实际测量过程中各种误差干扰使得d1≠d1m,d2≠d2m,…,dn≠dnm。由式(16)可求出di与dim的差值Δdi,Δdi/d的比值越大时,测距值di相对误差越大,对最终的定位结果影响越大,定义评价函数J1:
(17)
其中δ1为评价函数J1的系数。为进一步提高定位精度,需要剔除因物体遮挡导致误差较大的参考节点的定位数据。定义评价函数J2如下:
(18)
其中δ2为评价函数J2的系数。当Δdi/di≥J1或Δdi≥J2时,说明由参考基站(xi,yi)引起的误差较大,则去掉AGV与该参考基站的测距数据。若Δdi/di 根据上面的推导,本文提出的定位算法具体描述如下: 1)目标节点AGV向所有参考基站发起测距,通过式(1)可以获得AGV到n个参考基站的距离分别为d1,d2,…,dn; 2)由最先测距完成的3个参考基站根据式(14)计算出目标节点AGV的初始位置(xD0,yD0); 3)通过最小二乘和泰勒展开的定位算法求出目标节点的初定位结果。将(xD0,yD0)代入矩阵G和H中,由式(10)可以求出目标节点的估计位置(xDi,yDi),作为目标节点的估计值(xDi,yDi),如果不满足终止条件Δx+Δy≤ε的话,则利用式(12)对(xDi,yDi)进行更新,从步骤(10)重新开始计算,直到满足误差要求,最终求出的(xDi,yDi)即为目标节点的初定位结果(xD,yD),初定位结果对精度要求不高,因此ε可以设置较大,一定程度上减少计算量。 4)通过式(15)计算出的初定位结果(xD,yD)到各参考节点的计算距离d1m,d2m,…,dnm,通过式(16)可以求出(xD,yD)到参考基站(xi,yi)的计算距离dim与测距di之间的距离差Δdi; 5)使用式(17)和式(18)分别求出评价函数J1和J2,对测距数据进行筛选:若Δdi/di≥J1或Δdi≥J2,则去掉误差较大的参考基站(xi,yi)及其测距di的定位数据,若满足Δdi/di 为了验证和比较算法的有效性,以UWB通信定位系统为例,使用Matlab进行仿真,仿真环境为智能仓储环境中的6 m×4 m的区域,假设AGV与参考基站在同一平面上,如图3所示的12个节点作为参考基站,参考基站1到基站12的坐标值分别为(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),(4,2),(4,4),(6,0),(6,2),(6,4),参考基站节点用符号“◇”表示。 图3 参考节点坐标图Fig.3 Coordinate diagram of reference nodes 对文献[9]基于泰勒展开的UWB定位算法和本文改进的算法进行对比。在下面数据仿真图中,约定:算法A为文献[9]中的定位算法,算法B为本文改进之后的算法。由前面章节的分析可知AGV与基站之间测距di与真实距离ri之间存在误差λi,仿真时需要考虑测距误差λi对计算结果的影响,根据参考文献[16]可知真实距离为(10±3) m时,室内无遮挡测距情况下正常的测距误差一般不超过0.15 m,而室内有遮挡的情况下根据遮挡物体材料不同误差也不同,一般为无遮挡测距误差的2-6倍。 定义ei为第i个目标节点的定位误 差,(xRi,yRi)为目标节点i的真实坐标, (xDi,yDi)为实际计算的坐标: 图4 算法A和算法B的定位结果图Fig.4 Location results of algorithm A and algorithm B 为验证算法有效性,对整个实验区域进行全面测试,在X轴和Y轴方向上每间隔0.5 m设置一个目标节点,总共设置96个目标节点,分别采用算法A和算法B进行定位。假设基站2受物体阻隔等因素影响,与AGV的测距误差为0.6 m,其它基站与AGV的测距误差随机生成为小于0.15 m的数据。经试验设置评价函数J1的系数δ1=8,评价函数J2的系数δ2=2.5。定位结果如图4所示。 图5所示为采用算法A和算法B对每个目标节点进行定位的误差分布图。可以看出采用算法A得到的定位结果误差基本集中在0.1-0.2 m,平均误差0.129 0 m。采用算法B的定位误差基本在0.1 m以下,平均误差0.072 8 m,相比于算法A定位精度提高了46.43%。图6所示为对算法A和算法B进行多次实验的平均误差对比结果图。 图5 算法A和算法B的定位误差对比图(基站2与AGV测距误差为0.6 m)Fig.5 Location error compare diagram of algorithm A and algorithm B(When the distance error between station 2 and AGV is 0.6 m) 图6 算法A和算法B的平均误差对比图(基站2与AGV测距误差为0.6 m)Fig.6 Average location error compare diagram of algorithm A and algorithm B(When the distance error between station 2 and AGV is 0.6 m) 假设AGV与基站2的测距误差为0.75 m,与其它基站测距误差随机生成小于0.15 m的数据,参数设置不变。采用算法A和算法B对每个目标节点进行定位的误差分布如图7所示,其中算法A定位的平均误差为0.154 5 m,算法B定位的平均误差为0.067 3 m,定位精度提高56.44%。 图8所示为AGV与某个基站间不同测距误差时,算法A和算法B的平均误差对比图。实验证明测距误差越大,算法B的效果越明显。 图7 算法A和算法B的定位误差对比图(基站2与AGV测距误差为0.75 m)Fig.7 Location error compare diagram of algorithm A and algorithm B(When the distance error between station 2 and AGV is 0.75 m) 图8 不同测距误差下算法A和算法B的平均误差对比图Fig.8 Average location error compare diagram of algorithm A and algorithm B with different distance error 对基于UWB无人运输车的室内定位的误差进行了分析,改进了现有的最小二乘和泰勒展开的定位算法,设计了一种评价函数方法筛除误差较大的测距数据。实验证明该方法计算量较小,定位精度相比传统基于最小二乘和泰勒展开的定位算法能提高50%左右,当AGV与基站的测距误差越大时,该方法的改进效果越明显。2.4 算法描述
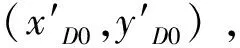
3 仿真及分析
4 结语

