基于互相关的仿真算法(CCSIM)的页岩 数字岩心重构

崔帅飞，张心罡，罗建鸿，王润涵，聂 昕,2＊

1长江大学地球物理与石油资源学院，湖北 武汉

2非常规油气湖北省协同创新中心(长江大学)，湖北 武汉

页岩，数字岩心，基于互相关的仿真算法(CCSIM)，图像重构

1.引言

页岩油气是潜力巨大的非常规油气资源，其勘探开发对解决能源问题具有战略性意义。由于页岩储层低孔、低渗，且孔隙多为纳米级[1]，各向异性突出，结构组分复杂，常规岩石物理实验难以展开，页岩气勘探的基础理论研究受到了制约。数字岩心是近几年兴起的岩心分析方法，其基本原理是基于二维扫描电镜图像，运用计算机图像处理技术，通过一定的算法完成数字岩心重构，为基于数字岩心的岩石物理特性数值模拟奠定基础[2][3]。目前，应用的重构方法多以低阶统计描述为基础，无法提供关于非均质多孔介质的准确信息。此外，高分辨率二维多孔介质薄片图像的可用性较低，成本较高，计算困难，甚至无法获得完整的三维图像，所以重构二维多孔介质薄片仍是一个尚未解决的重要问题。通过对比前人的研究结果[1][2][3]，笔者利用基于互相关的仿真算法(CCSIM)，基于二维切片进行二维图像的重构，为三维多孔介质图像的重构提供基础。

2.数字岩心重构方法

目前数字岩心建模方法主要包括物理实验法和数值重构法。其中，物理实验法又可细分为序列成像法、X射线计算机层析成像扫描法和聚焦离子束电子显微镜扫描法等，使获得岩石样品的三维图像成为可能。但物理实验法也存在许多问题：仪器的分辨率低，费用昂贵，费时费力，局限性较大等，只能进行特定岩石样品模型的构建，无法随意根据建模需要调整岩石的孔隙度等参数。数值重构法较为灵活，借助岩心二维图像等资料，通过图像分析，提取建模信息，建立数字岩心，可分为过程法和随机法。Bryant等[4]提出了过程法，该方法利用岩石二维图像的分布信息，通过模拟沉积岩的沉积、压实和成岩作用等一系列过程，从而建立三维数字岩心。随机法包括完全随机法、高斯场法、顺序指示模拟法、模拟退火算法、多点统计法和马尔可夫链–蒙特卡洛法(MCMC)、CCSIM等。

CCSIM实现了砂岩和碳酸盐岩数字岩心的重构[5]，重构图像中的孔隙分布和多点连通性概率等均与原图像显著相似，表明了重构模型的准确性及CCSIM的可行性。为此，笔者利用CCSIM进行页岩储层重构，验证其在三维数字岩心建模中的可行性。

3.CCSIM重构原理

CCSIM使用一维光栅路径(图1)，在重构图像时为了保持图像各区域的连续性，在光栅路径上使用一个互相关(CC)函数[6]，以实现重构图像中多孔介质的连续性。在重构过程中，原始图像大小为m × m，记为Tm×m，在T中选取一块大小为n × n的区域并记为Dn×n，使用CC函数来量化Dn×n和Tm×m之间的相似度。具体步骤为：

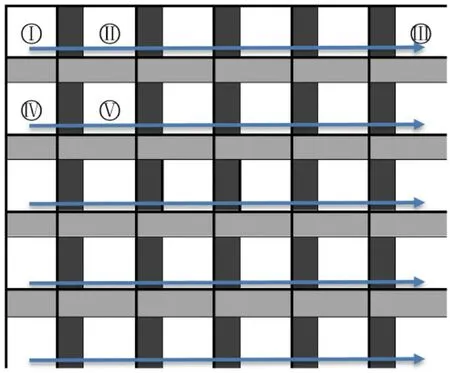
Figure 1.The diagram of one-dimensional raster path 图1.一维光栅路径示意图

1)初始网格G，使其具有P行和Q列的节点，各个节点为(p，q)，定义一个光栅路径。

2)在第一个节点处，在原图T中选择一个尺寸为n × n的区域为D。

3)从D中提取重叠区域O并将其与原图T对比，使用CC函数找到二者相关性高于阈值δ的点的位置，若满足条件的点数多于1个，则随机抽取其中一个点，基于该点的位置选择匹配的模式。

4)移动到光栅路径的下一个节点，将匹配的模式域赋给该节点处的D。

5)沿光栅路径重复步骤3)和4)，直到访问了路径网格G中的所有节点。

在D中提取重叠区域O时，若节点(k，l)位于网格的第一行(即图1中I～III区域)，则选择左侧D(1，l - 1)的右侧区域作为O(图2(a))。若节点(k，l)位于其他各行的第一列时(图1中IV区域)，则选择上一行D(k－1，1)的下部区域作为O(图2(b))；其余的节点处(图1中V区域)选择上一行D(k - 1，l)的下部区域以及左侧D(k，l－1)的右部区域作为O(图2(c))。选定O并与原图比较后，将在T中找到的位置处对应区域的模式赋给下一个D(k，l)。其中k和l取值范围分别为1 ≤ k ≤ p和1 ≤ l ≤ q。

Figure 2.The selection and matching of repeated region O 图2.重复区域O的选择方式及匹配方式

4.页岩储层数字岩心建模

根据CCSIM的要求，首先选取一块具有代表性的页岩岩样，在垂直方向上进行二维电镜扫描得到页岩原始二维图像切片(图3(a))，并对选取的切片进行逐点X光衍射矿物组分分析，用不同的灰度代表不同的岩石组分。在得到原始切片的矿物组分灰度图像后，应用CCSIM对其进行二维重构。先从原始图像切片中随机选取一个大小为50 × 50的区域，并将该区域定义在重构图像的左上角。由原始切片重构后的图像切片(图3(b))可以看出，重构后的图像与原始图像差别不大，骨架、孔隙及其他物质的分布特征基本一致，重构效果较好。

Figure 3.The comparison of two-dimensional image slice of shale 图3.页岩二维图像切片对比

5.结果分析

将原始二维图像与重构二维图像中各组分体积分数进行对比(表1)发现，多次重构图像中各组分体积分数均与原始二维图像有差别，且个别组分差别较大，主要原因是无条件重构没有硬数据(即与原图中状态完全一致的数据)限制，具有较大的随机性。因此，进行三维重构时需利用原始图像的硬数据限制重构图像，避免出现组分体积分数差别较大的情况。

自相关函数与图像的结构相关，是评价图像结构性质的重要函数[7]。通过对重构二维图像与原始二维图像进行孔隙组分的自相关函数对比(图4)可以看出，虽然部分组分的体积分数存在差异，但其分布特征与原始图像较为相近，说明CCSIM可为下一步页岩三维数字岩心重构提供基础。

Figure 4.The autocorrelation function comparison of each component between the original 2D and reconstructed 2D images 图4.重构二维图像与原始二维图像各组分体积分数的自相关函数对比

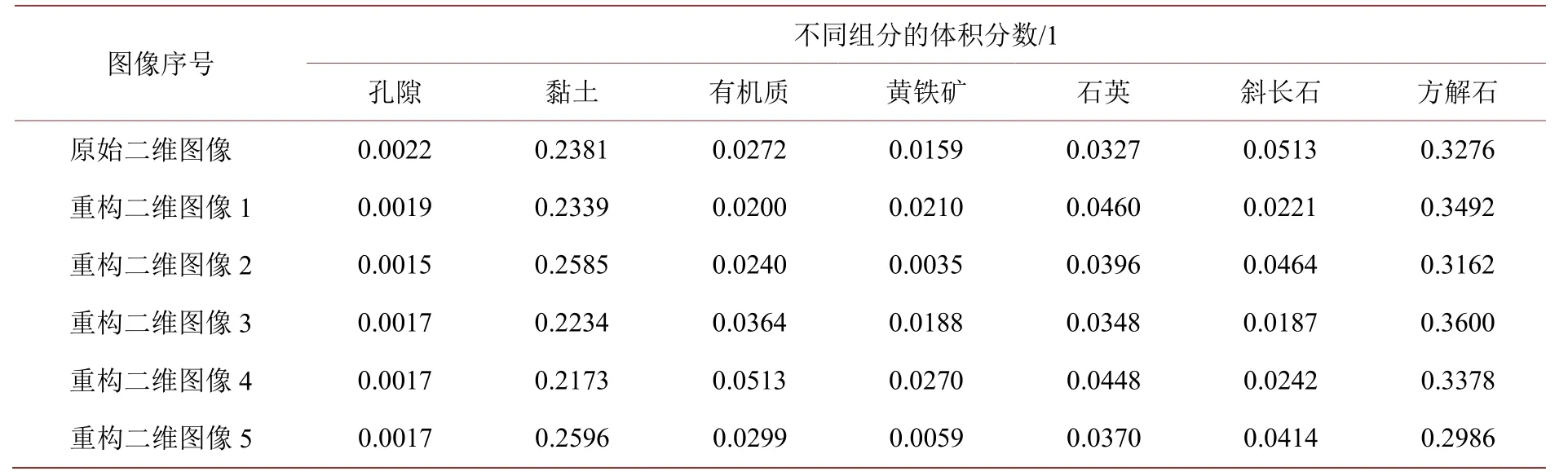
Table 1.The comparison of volumetric fraction of each component between the original 2D and reconstructed 2D images 表1.原始二维图像与重构二维图像中各组分体积分数对比

6.结语

数字岩心作为一种新的手段，可以弥补常规岩石物理实验的不足。笔者通过选用CCSIM重构了页岩二维切片数字岩心，并对重构结果进行了分析。CCSIM计算成本低、效率高、分辨率高，且能产生多个高度精确的组分分布，并且重构的图像复制了原始图像的结构、连接性及孔隙空间分布的可变性，重构效果较好。