城市空间网络的非连续性
——城市空间分区
杨 滔
引 言
20世纪后半期以来,世界各地出现了各种大规模开发项目,从而在一定程度上创造出新的城市形态。有些大型项目与原有城市毫无关系,缺乏规划统筹;有些属于原有工业用地的更新,与现状城市肌理保持一致。不管情形如何,其结果是出现了大量彼此独立的园区或封闭小区,由高速公路将它们联系起来。
很多研究从社会经济、功能布局、物质形态规划或政治学等角度[1,2]探讨此现象,认为这种新区、园区或封闭小区是经济社会力量在空间的体现。然而,从物质空间形态角度看,对此缺乏深入的讨论[3,4]。我们是否可将此视为一种新的城市化空间形态,并认可它们是从传统城市化模式之中演变而来?抑或,这只是一种新的空间现象,从长远来看将会改变城市空间形态的发展?
针对这种现象,可提出几个新的空间问题。首先,大规模的城市片区发展对其周边城市肌理有何影响?这是否与其空间结构有联系?其次,城市未来这种片区化的发展方式是否将形成新形态的城市增长模式?或者这些片区最终将演变为历史城市中哪种整体有机的网络结构,并将成为城市化的重要特征?或者,这将是一种新的城市化,体现出片区自给自足和彼此隔离?
当然,这与更为宽泛的“局部—整体”问题密切相关,即绝大部分城市具有根据地名划分的分区结构,这常常构成了城市认知和运行的基础。在城市认知和体验过程之中,我们常常难以发现那些地名分区的边界。在城市空间规划和设计的历史上,这就存在两个最基本的问题:在空间意义上,城市分区是什么?那些分区如何聚集形成一个整体空间?

图1 / Figure 1从起始轴线A出发,其周边4、5、6、7步范围内的轴线(标示为深灰色)The axial Lines (coloured in dark grey) up to 4, 5, 6 and 7 topological depth away from A root line
在过去空间句法的研究之中,大型片区项目的边界受到其周边不同尺度的空间结构影响,这不仅体现在形态之中,也体现在功能之上。对于某些项目,其边界体现为强烈的非连续性,即在某个尺度上,项目本身与周边空间结构之间的差异非常明显。因此,我们提出研究问题,即是否存在句法模型可以识别出空间结构的不连续性,从而实现一种定义城市分区的方法。当每条街道简化为一个点,它们之间的交叉则简化为连接线。以某条街道为起点,从邻近的街道,逐步向外扩展,去看整个街道网络,这将有利于我们发现不连续的状况。最为简单的方式就是探索观测的半径与在对应半径下所遇到的街道总数。我们可假设,从某个街道扩散到周边其他所有街道的过程之中,所遇到街道的总数如果发生重大变化,那么这也许代表了街道网络中的非连续性。
本文采用两个步骤去验证这个假设。首先,以伦敦为例,从某条街道的角度,探索其他街道与那条街道的顺次连接关系;进而以伦敦、北京和伦敦道克兰区为例,研究每条街道连接周边街道的方式与半径变化之间的数学关系。选择这3个案例的原因在于:伦敦是典型的自由肌理且演变上百年;北京则是典型的方格网的历史城市;道克兰区则是20世纪80年代西方最大的城市更新区,包括不同的片区项目。这将有助于我们在更为多样的背景之下,研究街道向外连接扩展的方式,获得普遍性结论。
其次,以某个轴线图为例,从理论角度探讨从某条街道顺次连接到其他街道的过程之中,是否可发现重要的断裂点,并检验这是否符合轴线图上的非连续性。然后,本文审视金丝雀码头项目,从实证的角度看看是否能发现该码头地区与其周边是否存在非连续的断裂。这将有助于我们根据街道顺次连接的速率去识别空间网络的非连续性。基于此,本文继续研究了伦敦、北京、伦敦道克兰区、伯明翰、芝加哥以及阿姆斯特丹等案例,期望发现更为普遍性的规律和空间机制。
嵌入轨迹
首先从一条轴线开始,随半径的增大,观察与之顺次相连的轴线如何变化。这使得我们可直观地研究某条街道融入周边街道网络的方式。如图1所示,随机选取伦敦轴线图上的一条轴线A作为起始轴线,计算该轴线到其他所有轴线的拓扑距离,并分别标示出距离该轴线4、5、6、7步数的所有轴线,用深灰色线条表示。

图2 / Figure 2基于轴线模型,街道总数与半径之间幂函数关系大体适用于伦敦、北京和伦敦道克兰区(从左至右)上:R2值的分布模式;下:幂指数的分布模式,红色表示中值The approximated power-law relation between Node Count and Radius within the tested radius ranges for more than half of the axial lines in London, Beijing and the London Docklands (from left to right)Top: the distribution patterns of the R-square in correlating node count and radiusBottom: the distribution patterns of power-law exponent αRed line highlights the median value respectively
实际上,图1大体上展示了某条轴线从拓扑4步到拓扑7步,顺次融入周边的轨迹,称之为拓扑嵌入轨迹。基于类似米制距离计算的线段图,我们提出了米制嵌入轨迹,用于描述任意街道段根据米制距离顺次融入周边街道肌理的过程。不管是拓扑,还是米制距离,抑或角度距离,这种嵌入轨迹都可用于揭示街道与其周边街道在不同尺度下的关联变化过程。
那么,是否可以采用定量的方法去描述街道的嵌入轨迹?以伦敦、北京以及伦敦道克兰区为例,进行探讨。伦敦和北京的轴线图半径—半径均为10 (半径—半径等价于轴线图中最为整合的轴线的平均拓扑深度,在该半径下轴线图本身的边界不会过度影响分析结果[5]。因此,拓扑半径测试范围从1到10,避免轴线图边界的影响,而道克兰区的半径—半径则为19,因此测试范围从1到19。
对于基于米制距离计算的线段图,3个案例系统中的米制半径大概都是10km,因此选择分析范围为400m到8,000m,其间隔为100m,以此避免系统边缘的影响。
对于每个轴线或线段,在某个半径下所遇到的所有轴线或线段被定义为街道总量。街道总量与半径的双对数分析用于揭示它们之间的关系。在3个案例中,我们都发现双对数分析之中,街道总量与半径存在非常强的相关性,R2值接近1。因此,它们之间的关系可采用如下公式表达。


其中,α是幂指数,而H是规模常数。轴线分析表明,每个案例中一般以上的轴线都存在街道总数与半径之间的幂函数关系[6]。图2分别显示了3个案例中轴线图的R2值和幂指数。伦敦R2值的中值是0.985,北京的是0.977,道克兰区的是0.981。如果R2值要求高于0.970, 对于73.6%的伦敦轴线、59.4%的北京轴线以及69.4%的道克兰区轴线,它们的街道总数与半径之间都存在幂函数关系。如果R2值要求高于0.900,这3个案例中几乎所有的轴线都具备上述幂函数关系。这表明,从拓扑半径1到半径—半径范围之内,3个案例的拓扑嵌入轨迹符合幂律法则。
线段分析也得到类似的结论。图3分别显示了3个案例中线段图的R2值和幂指数。伦敦R2值的中值是0.993,9,北京的是0.993,7,道克兰区的是0.992,8。如果R2值要求高于0.99,对于74.4%的伦敦线段、68.5%的北京线段以及63.2%的道克兰区线段,它们的街道总数与半径之间都存在幂函数关系。如果R2值要求高于0.900,这3个案例中每条线段都严格遵循幂函数关系。对比轴线图,3个案例的线段图具备更为明显的幂律关系。
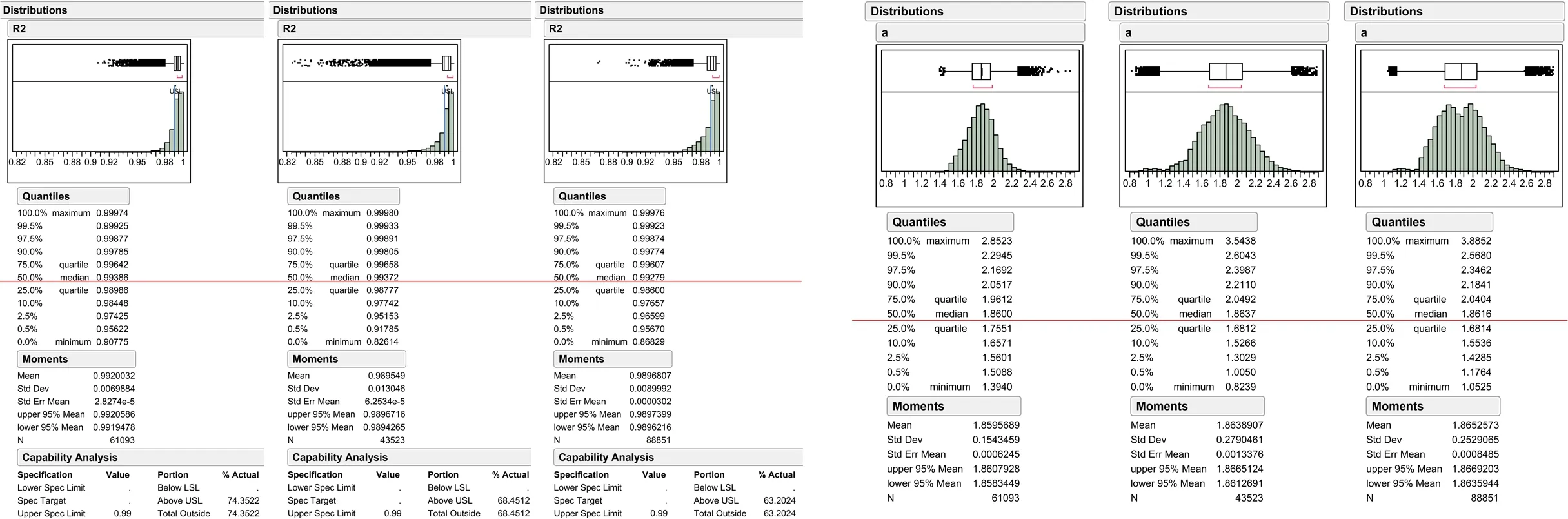
图3 / Figure 3基于线段模型,街道总数与半径之间幂函数关系大体适用于伦敦、北京和伦敦道克兰区(从左至右)上:R2值的分布模式;下:幂指数的分布模式,红色表示中值The approximated power-law relation between Node Count and Radius within the Tested Radius Ranges for more than half of the axial lines in London, Beijing and the London Docklands (from left to right)Top: the distribution patterns of the R-square in correlating node count and radiusBottom: the distribution patterns of power-law exponent αRed line highlights the median value respectively
然而,需要注意到,上述幂律关系只是统计结果,即如果R2值为0.9,这表示90%的街道总数与半径变量之间的关系符合幂律规则。其他的研究表明,拓扑或米制距离的嵌入轨迹可以由两个变量的韦伯分布来描述[7]。
嵌入轨迹的非连续性
嵌入轨迹上是否会存在非连续性的断点?也就是街道总数与半径之间的幂函数关系是否存在突变?我们采用一个理想的轴线图去研究(图4)。我们从轴线图的R轴线去审视整个系统,将其转化为以R为起始点的示意图,其中点表示轴线,线表示轴线之间的相交关系。示意图一共有6层,A所在的第三层和B所在的第四层之间存在明显的断点,这表明从第一层到第三层的轴线在拓扑上距离轴线R更近,或者第三层之下的轴线更为聚集为一团。实际上,轴线图表明轴线图明显被轴线A分为两块。
图4右下是散点图,横轴是半径,纵轴是街道总数。可发现,半径3是突变点,即街道总数的增加速率明显发生了较大变化。这条散点图示与图5左侧的示意图非常类似,都可表明嵌入轨迹。因此,该轨迹上的非连续性断点可以采用街道总数和半径之间的散点图来识别。
根据嵌入轨迹的非连续性,我们可以从空间肌理的角度定义城市分区。如果一组相邻的空间(由轴线或线段表达)在各自的嵌入轨迹上存在类似的非连续性断点,这表明这一组空间与其周边的空间分割开来,从而将它们定义为一个城市分区。
幂律关系的细微变化
以金丝雀码头为例,根据轴线或线段图的嵌入轨迹,可以探讨特定分区的边界的划定。为了避免系统的边界效应,金丝雀码头被放在轴线图的中央。轴线图分析的半径范围是1m~40m,线段图分析的半径范围是400m~8,000m,,其间隔是100m。图5是金丝雀码头的街道总数和半径之间的散点图。虽然这两个变量之间的R2值高达0.991,8,然而散点图并不是一条直线,而存在一些拐点。
我们试图探索幂律关系中的细微变化。首先选择散点图中最左下方的三个点,进行回归性分析。如果R2超过0.999,我们继续选择与之相邻的第四个点,再进行回归分析,检验R2是否超过0.999。如此反复,直到R2低于0.999。再选择上述分析中的最右上角的点,开展下一轮分析。依次操作,直到所有的点都被分析一遍,从而得到幂律关系的分析半径范围及其对应的R2值。

图4 / Figure 4理想的轴线图中的非连续断左:理想的轴线图;中:依据轴线图转化的关系图,其中红线(R)为起始线;右:街道总数(Y轴)和半径(X轴)的散点图A discontinuity detected in an ideal axial map.Left: an Ideal Axial Map, Middle: a j-graph converted from the top axial map, if observing the system from the red line (R)Right: the scattergram of plotting node count Rk of the left J-graph, on the y-axis, against radius on the x-axis

表1 / Table 1基于轴线图,金丝雀码头的幂指数与其对应的半径范围 / Based on the axial diagram, the power exponent of canary wharf and its corresponding radius range.
表1 基于轴线图,金丝雀码头的幂指数与其对应的半径范围。(例如,半径范围1到6中,回归系数为0.999,斜率为2.123,等价于幂指数)
表2,基于线段图,金丝雀码头的幂指数与其对应的半径范围。
图5展示了在限定的半径范围之内,回归线几乎为直线,且R2为0.999,其回归斜率为α。表1显示了在拓扑半径范围1~7、7~17、17~25以及25~40内,分别对应了幂指数2.123、2.672、3.679以及1.088。这表明在更小的拓扑半径范围之内,街道总数与半径之间存在更为明显的幂律规则。
在上述双对数散点图中,拐点出现在拓扑半径7、17和25,即拓扑意义上的街道总数在3个拐点处发生了较大变化。换言之,金丝雀码头在这3个拓扑半径上遇到了更多的新街道,或者更少的新街道,这种半径拐点暗示着某种城市分区的空间定义。此外,半径7和17都小于19,这说明在这两个半径拐点上的非连续性并未受到轴线线图系统边界的影响。
线段图分析可以得到类似的结果。表2展示了在米制半径范围400m~2,700m、2,700m~3,700m以及3,700m~8,000m,分别对应幂指数1.575、1.237以及2.419。两个拐点出现在2,700m和3,700m,这代表了米制距离视角下的非连续性。
虽然金丝雀码头在较为宽泛的半径范围内,其街道总数与半径之间存在幂律关系,然而其嵌入轨迹上存在拐点。两两相邻的拐点之间存在接近完美的幂律关系。其轨迹上的拐点代表了金丝雀码头融入周边城市肌理的过程之中存在非连续性的过程,即在特定半径下将会突然遇到更多(或更少)的街道。因此,街道总数与半径的双对数散点图提供了一种定量的方式,根据特定分区周边不同尺度的城市肌理,去描述那个特定分区的边界。
周期性分区模式的生成
本文前部分表明,在伦敦、北京和道克兰区中,基于米制距离的线段分析相对于基于拓扑距离的轴线分析,揭示了街道总数与半径之间更为明显的幂律关系。因此,城市肌理的非连续性看似与米制距离更为相关。本文后半部分重点分析基于米制距离的线段图。

图5 / Figure 5基于轴线图(上)和线段图(下),街道总数和半径之间的幂函数关系在更小的半径范围内得以验证A Strong Power Law Relation between Mean Node Count of Canary Wharf and Radius Found within Smaller Radius Ranges, Based on the Axial and Segment Analysis

表2 / Table 2基于线段图,金丝雀码头的幂指数与其对应的半径范围 / Based on the axial diagram, the power exponent of canary wharf and its corresponding radius range
对于街道总数与半径之间的关系,幂指数等价于双对数散点图中的回归线斜率,那么幂指数其实等价于街道总数随半径变化的速率,即街道变化率。可假设,通过计算街道变化率,可识别城市空间网络中的分区现象或模式。
首先,我们从数学的角度定义双对数散点图中回归线的斜率(图5)。如果很小的半径范围为σ,那么从半径(k-σ)到 k所新增加的街道总数就是街道变化率。该变化率可定义为嵌入率,如下公式所表达。
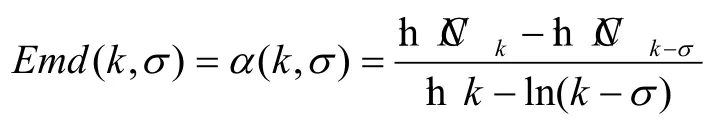
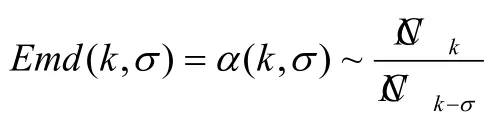
我们继续测试了阿姆斯特丹、芝加哥和伯明翰(图7),可发现同样的周期式分区。这看似是不同城市共有的现象,也可认为这源于街道总数随半径增长过程的变化率,体现出某种规则。
因此,周期性分区的现象可视为创造的现象,即在限制前提的实验过程之中,规律性的现象较为明显,并反复出现在不同的案例之中[8]。哈金(Hacking)认为只有在人类所创造的特定设备、计算方法或技术的前提下,创造的现象才会出现;这类似于约瑟夫森(Josephson)的超导现象。该现象的出现本身体现了设计和制造那些设备和计算公式的方法,因此该现象被视为“揭开宇宙奥秘的钥匙”,或“理论的核心对象”。周期性分区现象代表了城市不同尺度的规律性分区,如社区、邻里、片区、城市等。在某种意义上,数学计算的过程揭示了城市空间分区的机理,将来可用于解释城市局部和整体之间互动的关系。
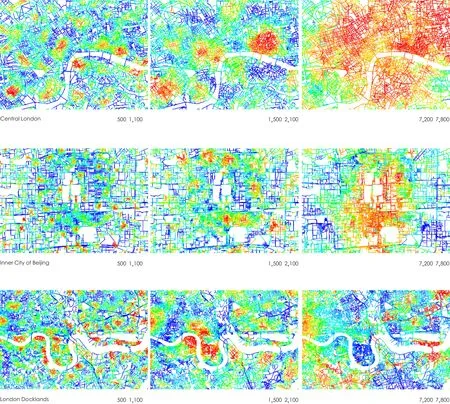
图6 / Figure 6依据米制嵌入率生成的伦敦、北京和道克兰区的周期性分区模式The Patchwork Patterns of London, Beijing and the London Docklands Generated by Metric embeddedness
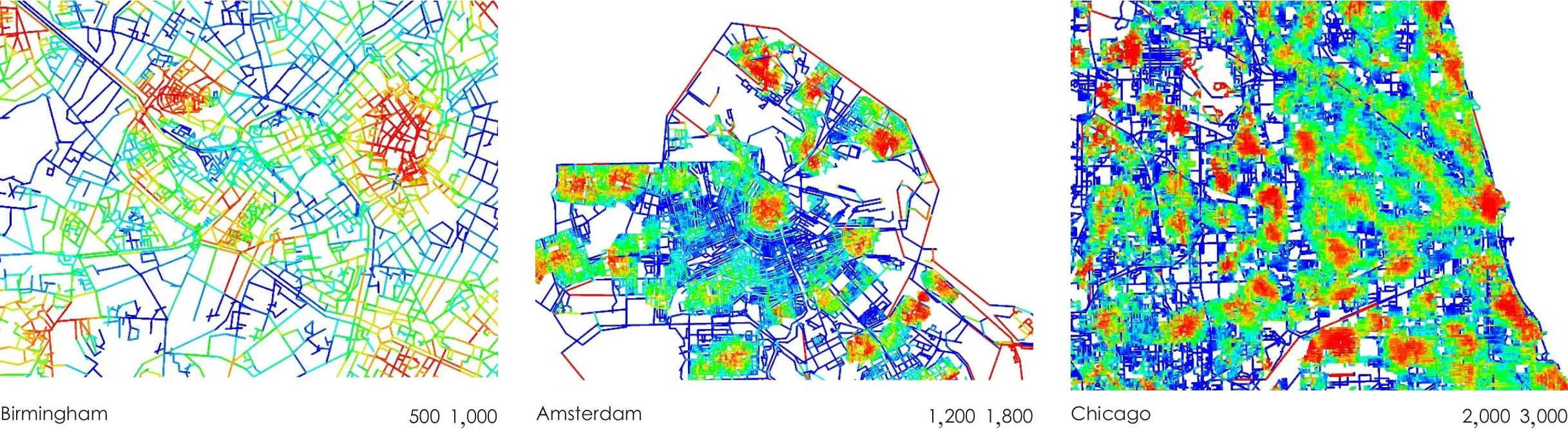
图7/ Figure 7依据米制嵌入率生成的伯明翰、阿姆斯特丹和芝加哥的周期性分区模式The Patchwork Patterns of Birmingham, Amsterdam and Chicago created by Metric Embeddedness
周期性分区模式表明,城市空间网络被分为离散型的地区,每片地区的周边都出现了城市网络的非连续性,即街道嵌入率发生较为明显的变化,这可称之为空间网络的非连续性。本文前半部分曾讨论,每条街道的嵌入轨迹刻画了该街道与周边街道的互动情况,其中的拐点代表了该街道与周边街道的连接程度发生了较为明显的变化。那么,周期性分区模式说明,对整个城市空间网络而言,属于同一分区的街道嵌入其周边街道肌理的速率类似,且具有类似的拐点。这表明周期性分区模式本身属于城市空间网络中每条具体街道与周边相互动中所突现的现象(emergent phenomenon)。
生成周期性分区的另一种方法
笔者和希列尔教授还发现另一种方法可生成周期性分区的现象。对于每条线段,可计算特定半径下的平均米制距离,即在特定半径k下,从所有线段到起始线段的米制距离的算术平均值,可表示为MMD Rk。
对比MMD和米制嵌入率所生成的周期性分区图,MMD在800m和1,800m半径下所生成的图从视觉上类似于米制嵌入率在500~1,100m和1,500~2,100m半径范围内所生成的图。不过,伦敦和北京的MMD在7,500m所生成的图与米制嵌入率在7,200~7,800m所生成的图并不一样。这种差异也在道克兰区案例中得以发现。这表明在不大的半径之下,MMD和米制嵌入率可生成类似的周期性分区图(图8)。不过,这只是基于3个案例的结论。
对比一下伯明翰、阿姆斯特丹以及芝加哥案例(图9)。伯明翰在750m的MMD图、阿姆斯特丹在1,500m的MMD图以及芝加哥在2,500m的MMD图都出现了周期性分区现象,且分别对应于伯明翰在500~1,000m的嵌入率图、阿姆斯特丹在1,200~1,800m的嵌入率图以及芝加哥在2,000~3,000m的嵌入率图。这再次提示,在较小半径下,米制平均距离和米制嵌入率是揭示的类似空间分区现象。
实际上,这提出了一个问题:既然米制平均距离(MMD)也许是度量分区内部的特征,而米制嵌入率度量偏重度量分区外部的特征,那么为什么这两个变量在较小半径下会生成类似的周期性分区的模式?这两个变量之间的关系如何?帕克[9-10]曾比较过这两个变量,认为如果街道总量与半径之间的关系严格服从幂律关系,那么这两个变量度量的是相同的内容。笔者从纯粹的解析几何角度,不管幂律关系是否存在,证明了这两个变量在特定的半径范围内度量的是完全一样的内容。简而言之,米制平均距离(MMD)本质就是度量两个特定半径之间街道总量的变化率,即米制嵌入率。此外,计算米制平均距离的半径位于计算米制嵌入率的半径范围之内。因此,从理论上来说,前者偏重计算分区内部的空间结构,而后者偏重计算分区内外之间的关联。
分区结构的几何形态机制
那么,周期性分区模式的涌现是否存在几何形体上的机制?这是否可用于解释城市地区的现象,如地名分区?首先,我们从理论上思考这些问题。正如希列尔教授所说(Hillier,1996, 2001),局部放置的物体,如隔断,将会在整体空间内产生结构化的影响,那么将会形成诸如整合度的中心,因此物体的摆放方式将会导致空间的变形。在此基础之上,笔者和希列尔教授提出了假设:周期性分区模式也代表某种空间的变形,源于物体的形状以及在空间的摆放方式。
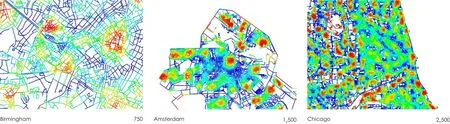
图9/ Figure 9依据米制平均距离,生成的伯明翰、阿姆斯特丹和芝加哥的周期性分区模式The Patchwork Patterns of Birmingham, Amsterdam and Chicago generated by Metric Mean Depth
为了验证假设,笔者和希列尔教授提出了探讨周期性分区的新方法,即MMD散点图,其中横轴是在半径n下的MMD,纵轴是在半径k下的MMD的倒数。这用于展示在整体空间网络的米制结构背景下,由MMD Rk所计算的局部米制结构的特征状况。我们发现了新的创造现象,称之为山型图,即MMD Rk在散点图中将形成山峰和山谷。图10显示了伦敦在1,200m和4,000m的山型图,解释了在这两个半径下的伦敦分区结构。较小半径下具有较多的小山峰,而较大半径下则只有少量的大山峰。
针对一个简单的方格网,其正方形边界视为对系统第一层次上的分隔。基于线段图,图11(右上)显示了在该方格网1/4直径下的周期性分区模式,红色表示较低数值,蓝色表示较高数值。4个较小红色分区位于方格网的四角,而较大的蓝色分区位于方格网的中央。红色分区的出现,是由于方格网的边缘限制了红色分区的线段获得更多较远距离的线段,而蓝色分区的线段则能获得更多较远距离的线段。
结合山型图进一步分析。选择山型图中最右侧的山峰,显示为黄色,那么4个角的红色分区同时被识别出来,也被显示为黄色。选择山型图中最左侧的山谷,那么中央蓝色的分区被识别出来。我们也把流程反过来,先选择周期性分区图中的红色或蓝色的分区,再研究它们在山型图中的哪些部位出现,是否呈现出山峰或山谷。山峰或山谷体现了MMD Rk的变化情况,说明了局部米制距离导致的结构变化。
山峰或山谷的形状可用于解释分区的几何机制。山峰的顶部代表最低的MMD Rk,而山峰的其他部分表示相对较高的数值。那么,山峰的几何形体含义是某个分区具备最为整合的中心,其米制平均距离从该中心向周边逐步增加;而山谷的底部则代表最高的MMD Rk,其他部分则表示相对较低的数值。于是,山谷的几何形体含义是某个分区具有最为整合的边缘,其米制平均距离从该边缘向中心逐步增加。
山峰和山谷本质上与密度的概念有关,因为局部层面上放置物体的方式带来了密度的变化。正如希列尔教授[5]所说的空间网络加密理论,减小街坊块大小(或加密街坊块)意味着减少了从任意一点到其他所有点的平均距离。对于城市空间网络,如果其几何中心的街坊块越小,该网络的整体平均米制距离越小;如果其几何边缘的街坊块越小,该网络的整体平均米制距离越大。本质上,这对应两种形态模式:“中心—边缘”模式,即中心的街坊块比边缘的更为密集;“边缘—中心”模式,即边缘的街坊块比中心的更为密集。前者米制整合度更高。
这两种模式对应于山峰和山谷。山峰意味着具有更为整合的山顶,对应于“中心—边缘”模式的街坊块密集中心;山谷则表示具有更为隔离的谷底,对应于“边缘—中心”模式的街坊块稀疏中心。这说明,根据不同尺寸的街坊块布局方式,山峰和山谷交替出现,对应两种不同的网络加密模式。
其次,我们继续采用句法的方法,去研究生成的分区功能意向。也许最简单的方式就比较生成的分区和事先定义的分区(如地名区)。过去的研究[6,13]表明它们之间存在视觉上关联性,同时也暗示了周期性分区模式具有功能内涵,可用于研究诸如地名区的城市功能分区。
希列尔和笔者[6,13]认为山型散点图可用于研究地名分区结构。以伦敦为案例,展开说明研究过程,并结合网络密集化理论去探索更多的内容。一方面,我们研究事先确定的分区如何在散点图中显示,目标是在整个网络的背景之下去研判该分区的形态特征。例如,选择伦敦老金融区,它立刻在散点图中显示为浅黄色的点群(图12);调整局部MMD的半径,直到山峰或山谷的第一次出现,如伦敦老金融区在4,000m时形成了山峰。这使得我们可探索事先定义的分区在多大尺度上具备形态、空间或功能上的作用。
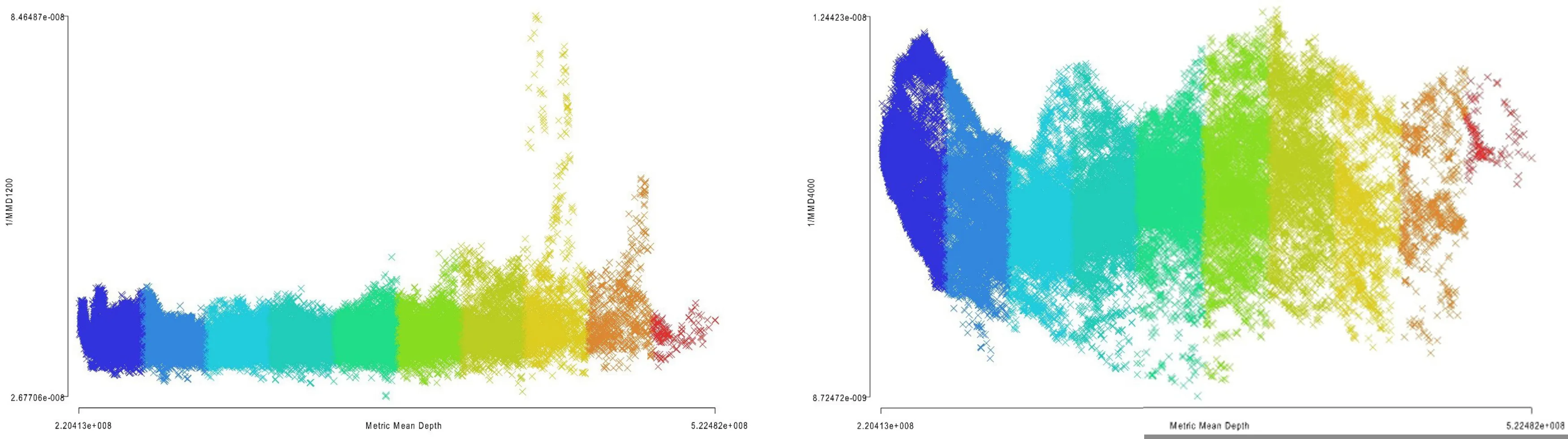
图10 / Figure 10伦敦1,200m(左)和4,000m(右)的山型图(纵轴为MMD Rk,横轴为MMD Rn)Two Mountain Scattergrams (plotting the reciprocal of MMD Rk, on the vertical axis, against the MMD Rn, on the horizontal axis) of London at 1200m and 4000m
另一方面,我们还可反过来操作。在散点图上选择山峰或山谷,检测它们是否对应功能上的分区。这些功能上的分区未必与地名区一致。例如,“中心—边缘”模式常常对应于商业区、市场区、餐饮区、娱乐区等城市活力地区;而“边缘—中心”模式则对应于高校区、高档住宅区、历史上封闭的社会住宅区、历史上的医疗区等。前者偏向热闹,后者偏向宁静。
讨论:方法论的框架
本文所讨论的句法将构成识别并探索城市分区的方法框架,重点强调分区内部结构与其周边不同尺度的空间结构之间的互动关系。一组技术的目标是根据事先确定的分区与其周边不同尺度的关系,精准描述该分区的特征。因此,这些技术称之为描述性技术,包括随半径增长的可理解度或协同度,以及双对数散点图。
另一组技术试图识别、显示并模拟分区结构,发掘生成分区结构的空间机制。因此,这类技术称之为生成技术。一般而言,这包括通过不同半径的嵌入度和米制平均距离(MMD)生成周期性分区模式的方法,以及通过山型散点图勾画山峰和山谷模式的方法。
这两个方面的技术不仅构成了研究空间分区的方法学框架,而且为探索城市网络非连续性提供了概念性思路。不管哪一种方法,尺度的变化是关键点。不同的社会经济功能对空间上的聚集和疏散有着不同的需求,从而折射在空间布局之中,大致可分为“中心—边缘”或“边缘—中心”模式。城市的空间分区结构随尺度而变化的结果,体现为一种空间结构的密度,因此分区的边界线则不是固定的,随不同尺度的密度变化而变化,称之为分区边界的动态性。
与之同时,那些社会经济功能的影响范畴或演变的时间段并不一样。那么,它们影响空间布局的能力、范畴、时长也不一样,从而导致了城市空间网络在不同尺度上相对复杂于弹性的分区现象,以便适应城市复杂的功能特征。因此,尺度、空间、时间在不同维度上共同影响着城市空间网络的生长演变过程,形成了各个城市在不同尺度上独特的空间分区模式。
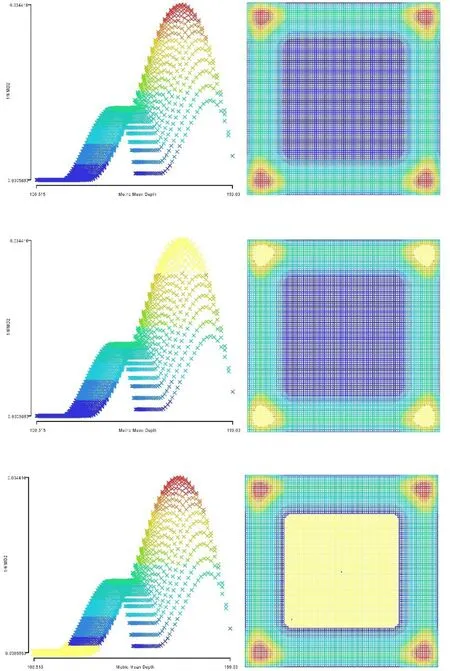
图11 / Figure 11简单方格网的山型图和分区模式,(红色对应山峰,蓝色对应山谷)The Mountain Scattergramms and the Patchwork Patterns of A Simple Square Grid (red patch corresponds to peak; blue patch denotes trough)

图12 / Figure 12伦敦金融区的山型图分析An Analysis of the Mountain Scattergram for the City of London
The Discontinuity in Urban Space Network:The Spatial De fi nition of Urban Areas
Yang Tao
In the final two decades of the twentieth century,cities in many parts of the world have been rapidly transformed through large-scale developments.Sometimes this involves the rapid expansion of an existing city outwards through a patchwork of large-scale separated developments with little co-ordinated planning. Sometimes it occurs within the fabric of the existing city through the re-use of previously industrial land. Either way, the outcome tends to be a patchwork of large-scale urban areas,with little relation to each other apart from being linked by a high speed road network.
This also is of course related to a broader background of the “part-whole” problem at the intra-urban level in cities: that in spite of the fact that most cities have some kind of named area structure, and this often seems important to the perceived character and functioning of the city, it is often very diffi cult to identify boundaries of named areas in the spatial form of the city. This has historically posed two fundamental questions for the theory and practice of urban spatial planning and design. What, in terms of space, is an urban area? And how do the areas aggregate to form a spatial whole?
We ask if there can be a syntactic method for identifying discontinuities in terms of space, and in this way arriving at a spatial de fi nition of urban area. Since the j-graph identifies the pattern of connection of the graph outward from each line or segment considered to be the root of the graph, we can ask fi rst whether the study of the j-graph can bring to light discontinuities in its outward growth.The simplest approach is to examine the relation between the radius of the j-graph and the sum of lines or segments encountered at that radius (called node count). The conjecture would be that any significant change in the pattern of growth in the number of nodes can perhaps represent a kind of discontinuity in the line or segment graph.
This article takes two steps to explore this conjecture. First, it quantitatively investigates the mathematical relation between the radius and node count of each line/segment, based on the cases of London, Beijing and the London Docklands,and meanwhile examines how a pre-given area is spatially embedded into the surroundings with increasing radius. This helps us to clarify the concept of discontinuity in terms of the change rate of node count. Second, it further explores the techniques for detecting the discontinuities in urban fabric with the aim of simulating the area structure, such as the named area structure. This study will be compared to Hillier's techniques for spatially differentiating urban areas, in order to elucidate the theoretical relationship between these techniques. This enables us to establish a synthesised framework for investigating the spatial mechanism involved in the spatial formation of urban areas.
All the syntactic methods can be placed together to establish a methodology framework for defining and identifying urban areas in terms of spatial con fi guration with the emphasis on the contextual structures. This will enable us to investigate the spatial formation of urban area structure (such as the named area structure).
One group of the techniques aims to describe what exactly a pre-de fi ned urban area (such as a named area) is, in relation to its contextual structures with increasing radius. In this sense, those techniques are termed the descriptive technique that can be used to detect whether, and if so how the spatial structuring of the urban area is influenced by its contexts. The other group of the techniques seeks to explore whether the area structure can be created, in such a way as generating linear structure such as integration core. Thus, they are called the generative technique that can be applied to explore the spatial mechanism for generating area structure.
On one hand, the descriptive technique includes the log-log radius plot, illustrating the logarithm of node count Rk on the y-axis against the logarithm of radius on the x-axis. Based on the axial or segment representation of urban network, it illustrates how node count varies with the radius, so that it can be used to trace the embeddedness trajectory on which a pre-given urban area (or even an individual line or segment) is gradually embedded into the contexts, in terms of its topological or metric distance to the surroundings, with increasing radius. Although the embeddedness trajectory can be expressed by a power law approximation, the different parts of embeddedness trajectory within several smaller radius ranges are governed by stronger power-laws. As a result, the in fl exion points along the trajectory imply the kind of discontinuities, in terms of the change rate of node count. This not only allows us to examine whether, and if so, how far the multi-scale contextual structures play a role in spatially defining urban areas, but provides a way of investigating and understanding the nature of the boundary of urban area.
On the other hand, the generative technique includes two methods of creating the periodic patchwork pattern by indexing the embeddedness or metric mean depth (MMD) values at different radii, as well as one method of producing the peaktrough pattern by creating the mountain scattergram. On this ground, the mountain scattergram,also created based on the segment model, offers a method of transforming the periodic patchwork pattern into the peak-trough pattern, and then examining the geometric and metric features of the created patches (or the pre-defined urban areas)against the metric pattern of the whole network of which they are the parts, in the light of the theory of grid intensi fi cation. We can use it to scrutinize the morphological relation between the created patches and the whole periodic structure, so that we can pave the way for a better understanding of the spatial mechanism of generating the periodic patchwork pattern.

