浅谈地理信息系统中的数据结构
蒋瑞祥
(安徽省合肥市新华学院国际教育学院,安徽 合肥 230088)
作为一类计算机系统,地理信息系统具有诸多功能,例如采集并存储地理信息,并通过筛选和归类信息实现地理信息的精准化应用[1]。现阶段,该技术已经广泛应用于国民经济的各个领域,包括国防建设、灾害放开以及通讯物流等。地理信息数据规模庞大,所以需要对目前的数据结构进行持续优化,这样才能提高地理信息数据的应用质量,并拓展其应用范围。
一、地理信息数据结构
一般情况下,通常将数据组织形式称作数据结构,这意味着数据结局能够描述数据集合结点之间的联系[2]。因此,数据结构在本质上属于非数值运算,主要涵盖队列、树木、线性表以及栈等内容。由此可见,地理信息数据结构主要指的是在计算机环境下显示地理信息数据的有效组织方式。
无论是地理数据模型还是地理信息数据结构都具有一定相似性,前者能够详细描述地理空间以及地理实体的本质情况,并将其信息转化为数据形态,在计算机作用下实现存储和处理。数据模型一旦形成,就需要相应的数据结构进行匹配[3]。按照计算及处理以及识别方式的差异,可将地理数据模型转化为两大数据模型,即矢量数据模型以及栅格数据模型。所以地理信息数据结构也具有以上两种数据模型形态。
二、基于表面表示的数据结构
基于表面表示的数据结构主要有四大类型,分别是格网结构(grids)、形状结构(shape)、面片结构(facets)以及边界表示(BR)
(一)格网结构
格网结构(grids)的应用较为普遍。地形表明通常有规则的mXn格网来展示,如图1所示。单个格网点对应一个高程值,格网点元素作为一个点,其常见于DEM中等高线的2.5D

图1
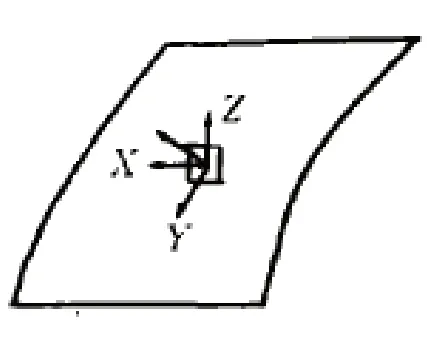
图2
(二)形状结构
形状结构主要借助对象表面点的斜率来显示,基本元素与表面上各单元的法线向量相匹配(如图2所示)。
该数据结构主要应用场景为3D重建,其逻辑在于单个像素明暗变化意味着地形坡度的起伏,因此可利用坡度变化波动来分析像素间的高差变化,进而确定精确的3D表面。
(三)面片结构
面片结构是借助不同形态的面片来描述特定对象的表面情况,面片主要有多种形态,例如正方形、不规则三角形以及泰森多边形等。不规则三角形的应用场景最为丰富,这是因为不规则三角形具有诸多优势,例如有效规避了等高线绘制过程中的“鞍部点问题”;计算坡度等相关参数的难度较小;此外,不规则点发布与样本实际情况相符,同时结束表面复杂性聊调节三角形的形态,通过这种方式能够保持良好的近似值。在面片结构中,将高程值整合三角形的顶点,则可以获得2.5D表示,如图3所示。
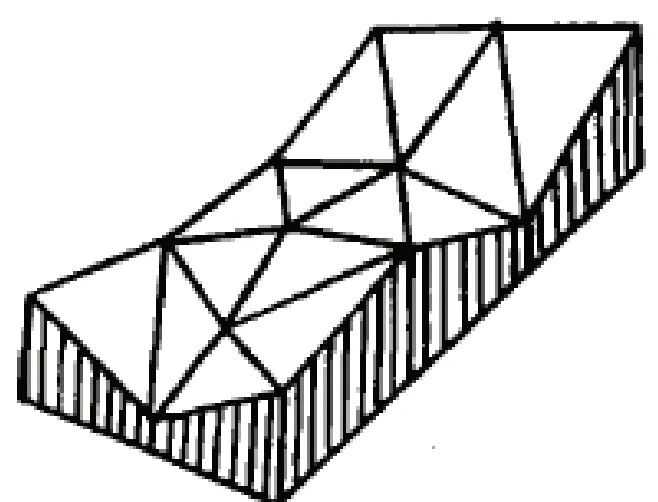
图3
(四)边界表示
边界标识是一种分级表示方法。在特定空间的事物均由四大元素构成,分别为点线面以及体,并且单个元素都可以借助几何数据、分类标志以及元素之间的关系进行描述。所以在实际场景中,需要首先确定元素之间的关系,这样才能将观测数据进行转化。由于地学研究对象通常以未知形态存在,因此元素关系的确定难度较大,甚至无法具备观测条件。因此边界表明在CAD/CAM系统以及工程等方面的应用极为少见。
(五)非均匀有理B样条(NURBS>函数
利用函数法来描述地学表明具有诸多优点,例如计算处理流程少,存储空间占有不高,还能保持空间唯一性。具体而言,非均匀有理B样条函数具有以下特征:
1、B样条的优势得以延续
2、竿视不变性—控制点透视前后的完全一致并且等价的。
3、蚯面等的精确表示只能实现近似描述,相对于NURBS而言,除了能够自由表示自由曲面,还能表示球迷。
4、多的形状控制自由度—NURBS给出更多的控制形状的自由度,通常可应用于多种形状的生成。
以上特征与3D GIS中有关面地表示需要保持一致,所以,在应用环节,NURBS的应用价值表现得更加突出,以上五类结构中其中边界描述可用来描述规则形状的对象,而其他四种则在描述不规则形状时更具优势,这说明不同结构具有相应的适用范围,需要结合实际情况具体应用。

