含矩形缺陷结构纤维全缠绕气瓶的爆破压力预测
王子文 赵建平 章 昕
(南京工业大学机械与动力工程学院,南京 211816)
文 摘 采用数值模拟与理论分析相结合的方式对含矩形缺陷纤维全缠绕气瓶的力学行为进行分析。基于Hashin 准则进行损伤模式表征以及损伤起始判定,并使用参数退化的损伤演化法则,使用FORTRAN 语言编写了适用于ABAQUS/Explicit 求解器的VUMAT 子程序。选择缠绕顺序为[90°2/18.9°2/90°2/28.9°2/90°2]纤维全缠绕气瓶为研究对象,分析矩形缺陷深度对于纤维缠绕气瓶应力水平影响。基于缺陷深度对筒体各层周向及轴向应力的影响,采用修正方法提出含缺陷纤维全缠绕气瓶爆破压力预测模型,模型预测结果与有限元模拟结果一致。对含不同缺陷深度的爆破压力做出预测,分析结果表明,当缺陷深度大于1.26 mm 时,爆破压力迅速下降,影响气瓶正常使用。
0 引言
纤维全缠绕气瓶因其安全、经济和高效在能源储运、航空航天、医疗领域发挥着重要作用。然而在服役期间,缠绕层的外表面容易因摩擦、碰撞等情况,产生凹坑、裂纹等缺陷。根据一份对某企业生产的车用气瓶的查验报告,不合格产品达总数的67%,其中外表面缺陷是导致气瓶失效的主要原因之一[1]。
Y.XU[2]对纤维全缠绕气瓶的常见损伤进行了分类,通过数值模拟给出了复杂损伤模式下的危险部位图,研究了不同部位以及尺寸的缺陷对结构应力分布的影响。郭崇志等人[3]针对含缺陷气瓶的有限元模型,得到含缺陷气瓶在最大充装压力下真实的应力分布,并研究了不同缺陷深度对纤维缠绕气瓶内衬层强度的影响。甘平燕[4]还研究了缠绕层中部出现不同长度和深度缺陷的CNG-2 气瓶,得到受内压载荷作用的缺陷气瓶的相对真实的应力分布。
本文针对含缺陷纤维全缠绕气瓶爆破压力预测问题,根据经典网格理论并结合实际情况,建立气瓶有限元模型,并基于Hashin 失效准则和参数退化方式编写VUMAT 子程序。以数值模拟为基础,提出理论计算公式,以期为含缺陷纤维全缠绕气瓶爆破压力预测提供一种准确、高效的预测方法。
1 复合材料渐进失效模型
1.1 复合材料失效起始准则
复合材料纤维及基体的损伤起始准则可由应力定义,也可由应变定义,C.H.HUANG 等[5]通过实验证明,使用基于应变的失效准则预测纤维与基体损伤起始要优于基于应力的失效准则,因为相对于应力而言,在材料失效过程中应变更为连续。因此采用基于应变的Hashin 失效准则[6-7]。
(1)纤维拉伸失效(ε11≥0)
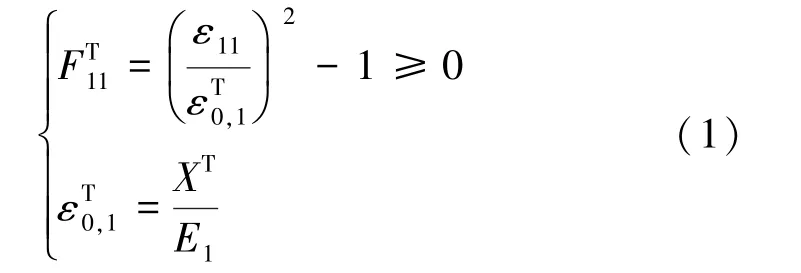
(2)纤维压缩失效(ε11<0)
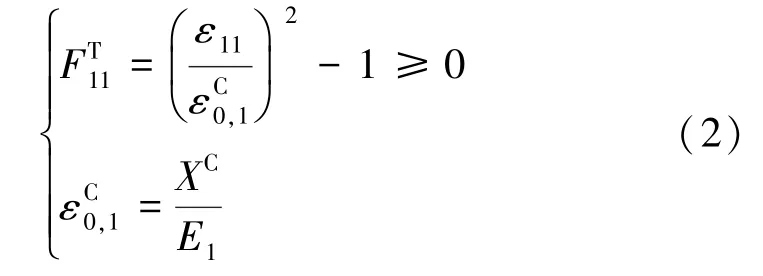
(3)基体拉伸失效(ε22+ε33≥0)
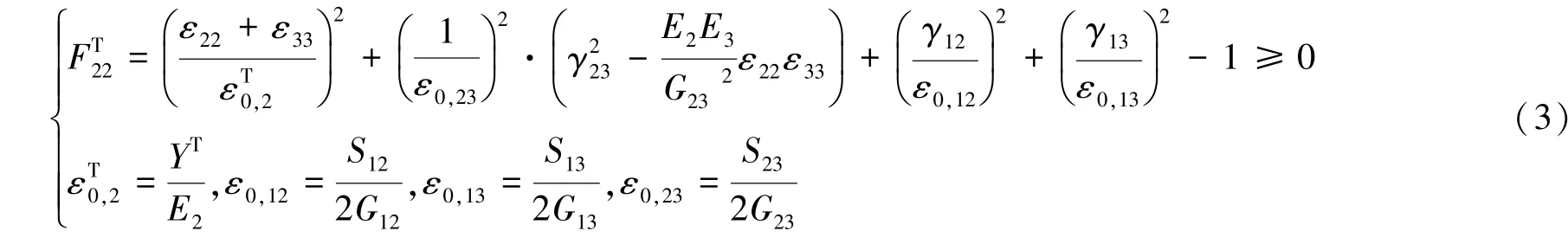
(4)基体压缩失效(ε22+ε33<0)
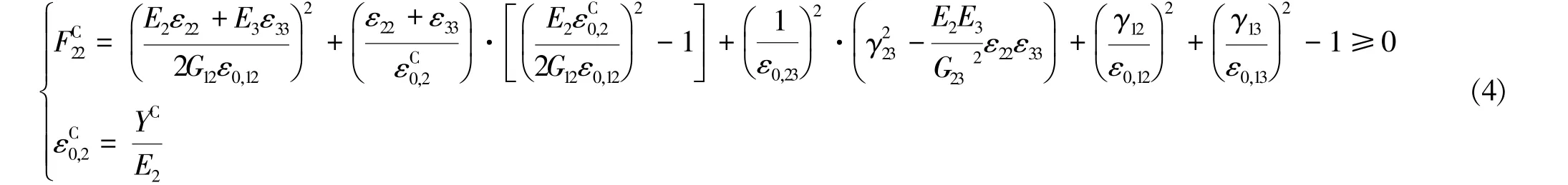
(5)分层失效(ε33>0)
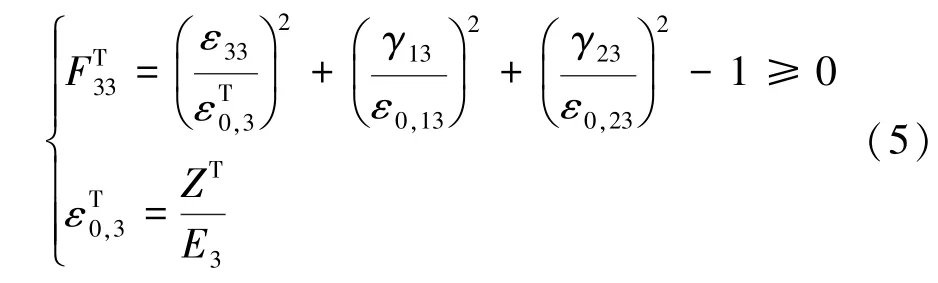
式中,FT11(FC11),FT22(FC22)为纤维拉伸(压缩),基体拉伸(压缩)失效因子。E1、E2、E3为弹性模量,G12、G13、G23为剪切弹性模量。XT(XC)为纤维拉伸(压缩)极限强度,YT(YC)为基体拉伸(压缩)极限强度,ZT为拉伸分层极限强度,S12、 S13、 S23为面内剪切强度,εT0,1(εC0,1)为纤维拉伸(压缩)失效起始时的应变,εT0,2(εC0,2)为基体拉伸(压缩)失效起始时的应变,εT0,3为拉伸分层失效起始时的应变,ε0,12、ε0,13、ε0,23为基体剪切失效起始应变。
1.2 参数退化准则
对于复合材料结构,单层发生损伤时,结构依旧具有承载能力,可通过对弹性模量折减的方式实现材料性能的退化[8]。当子层内任意铺层出现损伤时,依据表1提供参数进行退化。

表1 参数退化表Tab.1 Parameters degradation
2 含矩形缺陷纤维全缠绕气瓶数值模拟
2.1 含缺陷气瓶有限元模型
选用缠绕顺序为[90°2/18.9°2/90°2/28.9°2/90°2]纤维全缠绕气瓶为研究对象,内衬层尺寸如图1所示。筒身段的缠绕方式为环向缠绕和螺旋缠绕的组合方式,缠绕厚度均为0.42 mm。内衬材料为铝合金6061Al-T6,缠绕层为T700 型碳纤维增强材料,材料参数如表2、表3所示。
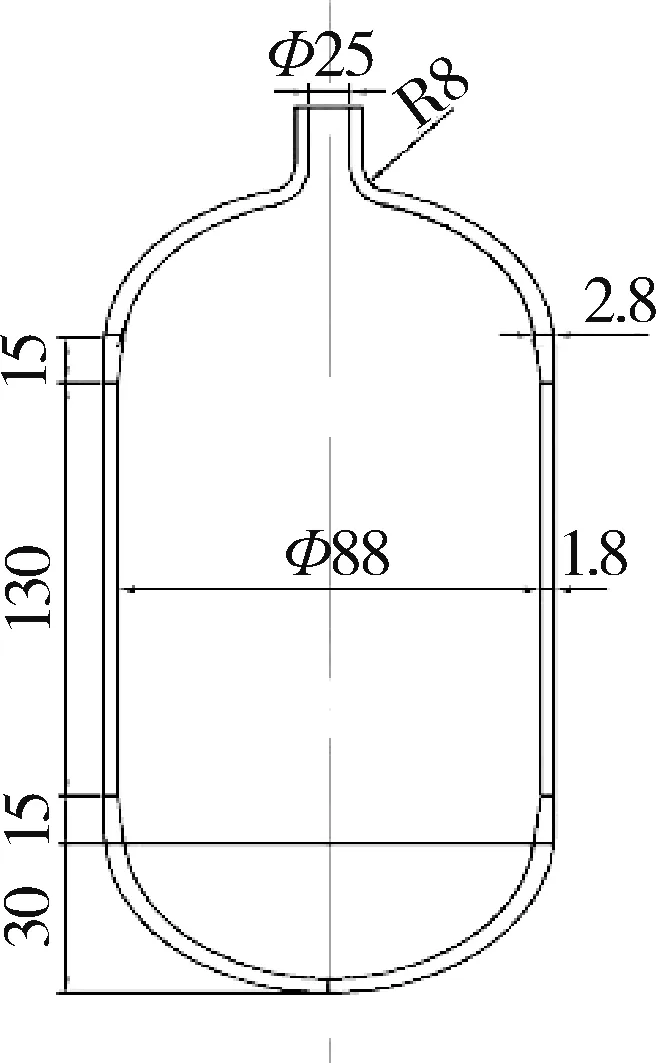
图1 内衬结构示意图Fig.1 Structure of the liner
根据GB24162—2009《汽车用压缩天然气金属内胆纤维环缠绕气瓶定期检验与评定》[9],复合材料层受到划伤、磨损时,判定当缺陷深度t0≤0.25 mm 时为一级损伤,属于合格产品;当缺陷深度0.25 mm、t0≤1.25 mm 时为二级损伤,属于可修复的缺陷深度;当缺陷深度t0>1.25 mm 时,为不合格产品。因此本文重点研究不同缺陷深度对气瓶承载能力的影响。气瓶最大应力出现在筒体中部,因此将缺陷设置在中部的缠绕层表面,有限元模型如图2所示。缺陷的轴向长度为11 mm,周向长度为16 mm,缺陷深度分别为0.42、0.84、1.26、1.68、2.1 mm。
图2 缺陷气瓶模型和局部放大图Fig.2 Model of composite cylinder with defect and local amplification

表2 铝合金6061Al-T6 力学性能[12]Tab.2 Mechanical properties of 6061Al-T6 aluminum alloy

表3 复合材料T-700/环氧树脂力学性能[13]Tab.3 Mechanical properties of T700/epoxy composite
2.2 有限元结果分析
根据X.ZHANG 等人[10]给出的爆破压力预测公式,得到爆破压力为125.8 MPa,而有限元计算结果为135 MPa,两者误差为7.3%,在工程允许误差范围内,因此说明了该模型的正确性,可以用于进一步分析外表面含矩形缺陷气瓶的承载能力的变化。
内压在123~133 MPa 时,周向及轴向应力增长幅度相对较大。所以施加的内压载荷自125 MPa 开始不断增加,直至爆破失效,分析缺陷深度对气瓶承载能力的影响。以外表面深度为2.1 mm 的矩形缺陷为例,与同等载荷条件的不含缺陷的气瓶比较,图3和图4为两种气瓶的变形及应力分布。
由图3可知,在125 MPa 内压作用下,不含缺陷的缠绕层筒体中部的轴向应力最大,且由内侧到外侧应力逐渐增大。在125 MPa 内压作用下,外表面含缺陷的缠绕层的轴向应力最大值明显高于不含缺陷的缠绕层应力,且结构出现应力集中。此外,复合材料层内侧的轴向应力分布也受到影响,缺陷对应部分的应力远大于附近区域,且轴向应力沿四周均匀增大。由图3(b)可知,沿缺陷周向方向的应力水平远低于轴向方向。
由图4可见,气瓶内衬层和缠绕层在缺陷处均出现了不同程度的鼓包变形。缺陷处复合材料层应力由内侧向外侧逐渐增大,且环向层的轴向应力明显高于螺旋层。在缺陷表面的复合材料层,虽然出现了结构的部分残缺,但是依然具有承载能力。
不断增加内压直至缺陷气瓶爆破失效,其轴向及周向应力的最大值随内压的变化见图5。由图中曲线斜率可知,缺陷气瓶的轴向应力随内压变大而大幅增加。在130 MPa 时快速增大,而周向应力随内压的增加先变大后稳定,最后在130 MPa 时快速增大,说明缺陷深度为2.1 mm 气瓶的爆破压力为130 MPa。为比较缺陷深度对气瓶影响,选择轴向和周向应力大幅增长,但5 个缺陷深度(0.42、0.84、1.26、1.68、2.1 mm)气瓶均未爆破失效的工况,即125 MPa 的内压载荷进行分析讨论。为了直观反映复合材料筒体上应力的变化,选择筒体上应力最大的缠绕层表面展开路径分析。
由图6可知,气瓶缠绕层的轴向应力随着缺陷深度的增加近似于线性快速增长。经研究发现,结构的周向应力最大值出现在气瓶底部,因此按照路径分析周向应力的最大值已不再合适,直接讨论应力极大值随缺陷深度的变化,如图7所示。在一定范围内缺陷深度的增加会导致最大周向应力的增加,但深度在较大范围内时应力保持在较高水平,增加趋于平稳。由此可知,缺陷深度对气瓶轴向应力影响相较周向应力更为显著。
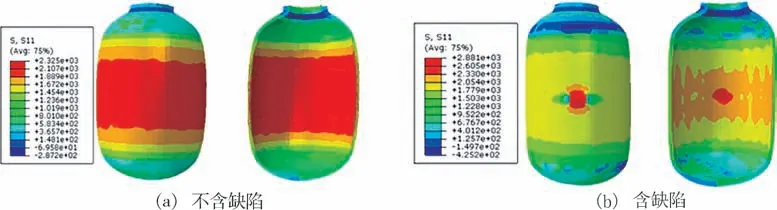
图3 复合材料层应力分布云图Fig.3 Axial stress distribution of composite layers

图4 缺陷部分的受力变形Fig.4 Deformation of the defect
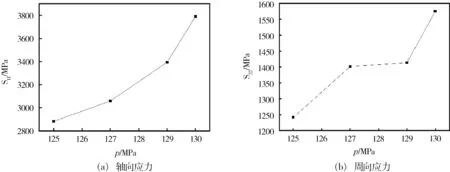
图5 缺陷深度为2.1 mm 的气瓶应力随内压的变化Fig.5 Stress of the composite cylinder with defect’s depth of 2.1mm
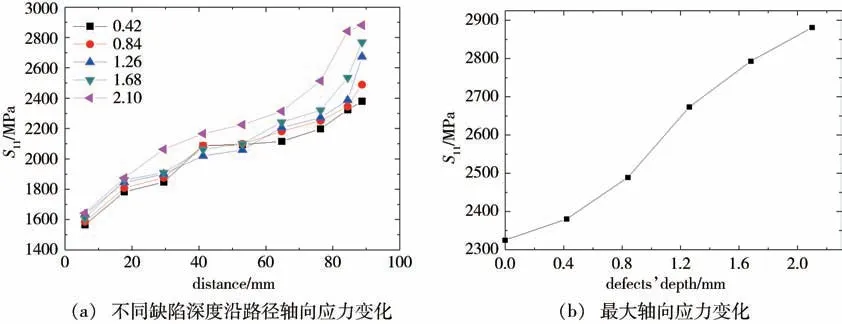
图6 轴向应力随缺陷深度的变化Fig.6 Changes of the axial stress with defect depeth
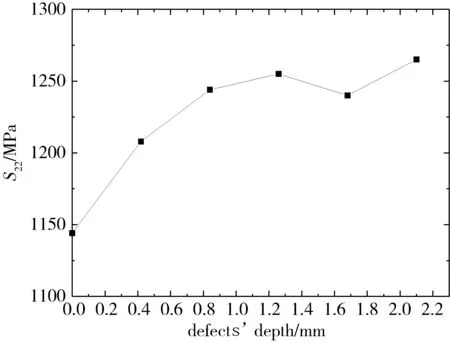
图7 周向应力随缺陷深度的变化Fig.7 Changes of the circumferential stress with defect depeth
3 含缺陷纤维全缠绕气瓶理论失效预测模型
3.1 含缺陷筒体逐层应力分析
由X.ZHANG 等人[10]得到的缠绕层筒体处最大允许工作压力的计算公式可知,单层复合材料层的承载能力很大程度影响着爆破压力。以缠绕层外表面含深度为2.1 mm 缺陷为例。在125 MPa 内压作用下,分别讨论完整结构气瓶和含缺陷结构气瓶各层的最大轴向和周向应力变化。
由图8(a)可见,含缺陷的环向层和螺旋层的轴向应力均明显大于不含缺陷气瓶,且同一缺陷气瓶,缺陷交界处的含缺陷部分的轴向应力明显降低,缺陷部分的环向层的轴向应力低于不含缺陷部分,部分轴向应力被分摊到不含缺陷部分的环向层。由图8(b)可见,含缺陷缠绕层的环向和螺旋层的周向应力均低于不含缺陷的缠绕层,缺陷交界处的含缺陷部分的周向应力呈现明显降低,缺陷部分的环向层的周向应力低于不含缺陷部分。
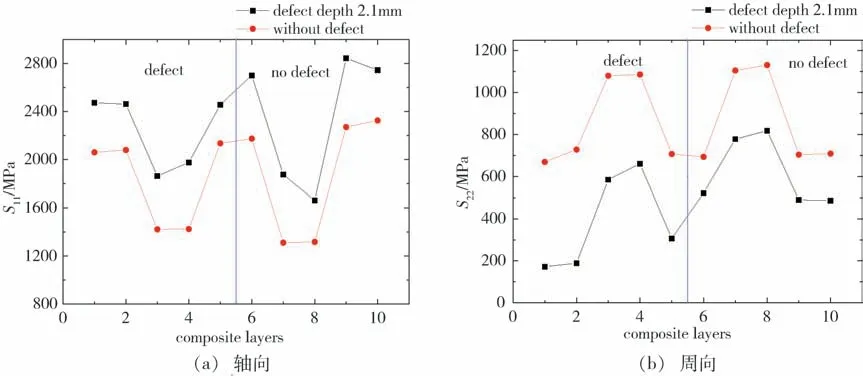
图8 含缺陷结构复合材料层逐层的应力变化Fig.8 Stress of each layer of composite cylinder with defect
3.2 爆破压力预测的修正方法
单层的缠绕层的最大允许工作压力计算式如下:
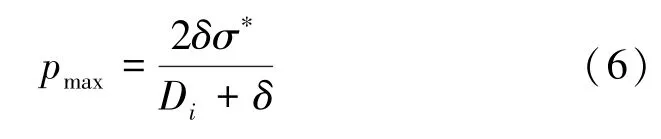
式中,δ 为缠绕层厚度,Di为内径,最大工作压力很大程度取决于复合材料圆筒的最大应力σ∗,且σ∗与铺层角度α 紧密相关,即方向角(θ = 90° - α)。一般认为以轴向应力S11为主导因素来判断是否超过结构横向拉伸强度XT,因此以缺陷对缠绕层的轴向应力的影响来修正第1、2、5、6、9、10 层的最大工作压力计算式;以周向应力S22为主导因素来判断是否超过结构纵向拉伸强度YT,因此以缺陷对缠绕层的周向应力的影响来修正第3、4、7、8 层的最大工作压力计算式。
已知研究对象的缠绕层的单层厚度为0.42 mm,缺陷深度为2.1 mm。定义同一角度正反交替缠绕的相邻两层合并为一层进行分析,由外侧向内侧的编号为[1、2、3、4、5],因缺陷交界处出现在合并后的第3层,即原来的第5、6 层,应该分开考虑,因此缺陷气瓶的缠绕层由外侧向内侧的编号修改为[1、2、3(前1/2)、3(后1/2)、4、5],其中1、3(前1/2)、3(后1/2)和5 为环向缠绕层,2 和4 为螺旋缠绕层。环向层的轴向应力S11和螺旋层的周向应力S22的具体数值以及承载能力的变化,如表4所示。
由数值模拟结果可知,缠绕层的应力是由内侧向外侧逐层增加的,为避免应力逐层增加对于出现缺陷后缠绕层的应力增加现象的干扰,另外考虑到最内侧缠绕层一般不会出现局部减薄缺陷,选择最内侧的第5 层环向层和第4 层螺旋层作为参考,将外侧缠绕层的应力与内侧作为参考缠绕层的应力相除得到应力比γ,将不含缺陷气瓶的应力比γ0减去含缺陷气瓶对应层的应力比γ1,得到相同内压下,含缺陷气瓶缠绕层的各层承载能力下降系数φ,具体结果见表4。
缺陷的交界处位于第3 层,根据表4可得,不含缺陷的环向层轴向应力虽然逐层增加,但是幅度很小基本平均分布,而在含缺陷结构的环向层中,缺陷部分的轴向应力比γ1在同一水平,不含缺陷部分的环向层的轴向应力比γ0也在同一水平,但是γ1相较于γ0下降明显,说明缺陷对环向层承载能力的削弱作用。含缺陷结构的螺旋层S22应力低于不含缺陷的缠绕层,其缺陷部分的螺旋层的周向应力的应力比γ 下降显著,说明缺陷对螺旋层承载能力的削弱作用。
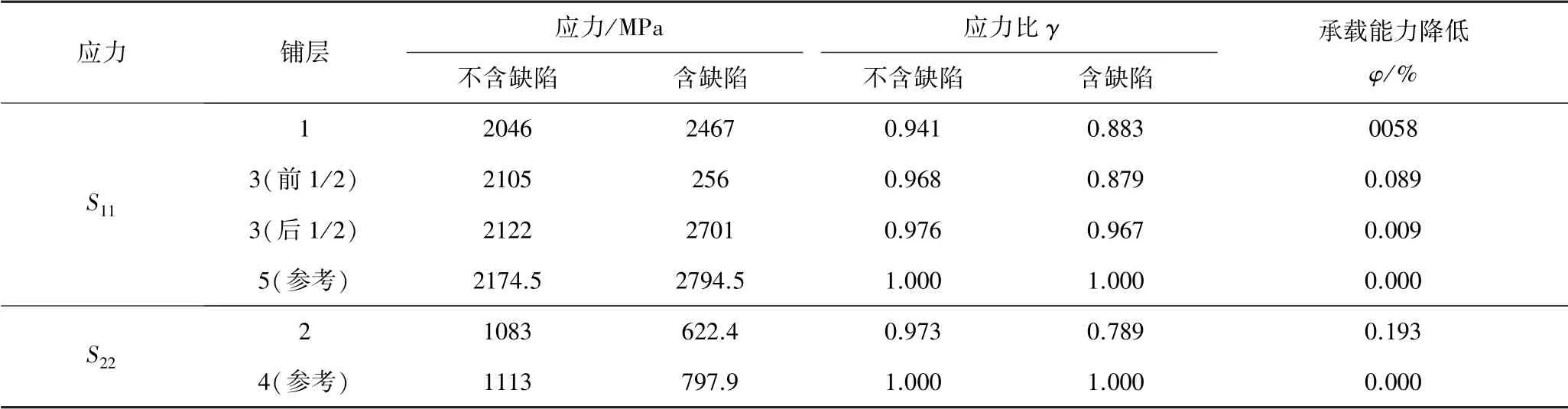
表4 缠绕层各层应力和承载能力Tab.4 Stress and bearing capacity of each layer of composite cylinder
纤维全缠绕气瓶的最大允许工作压力,可根据不同铺层角度的单层缠绕层筒体联合计算得到:

基于式(6),将各层下降的承载能力下降系数φ代入公式中,可以得到含缺陷结构的单层的复合材料圆筒的最大允许工作压力:
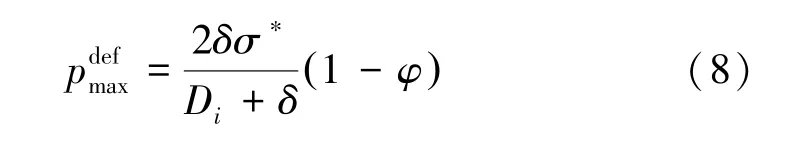
基于式(7),含缺陷结构的多层缠绕的纤维全缠绕气瓶的最大允许工作压力,可根据不同铺层角度的含缺陷结构的单层缠绕层筒体联合计算得到:
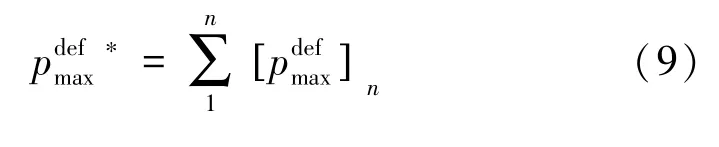
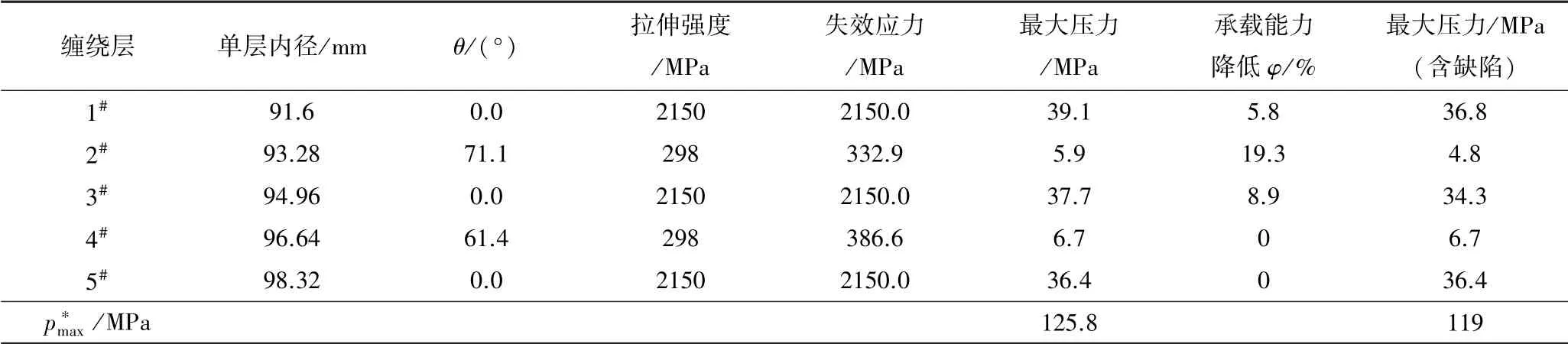
表5 含缺陷结构的复合材料圆筒的最大压力Tab.5 Maximum pressure of composite cylinder with defect
基于式(9)该缺陷气瓶的各层缠绕层的最大工作压力的计算结果如表5所示。含缺陷的纤维全缠绕气瓶的爆破压力的计算值为119.0 MPa,相比不含缺陷的纤维全缠绕气瓶,爆破压力下降5.3%。由模拟结果可知,该缺陷气瓶的数值模拟得到的爆破压力为130 MPa,爆破压力下降3.7%,爆破压力的降低程度的理论解与有限元解接近,说明含缺陷纤维全缠绕气瓶最大工作压力计算式的修正方法的正确性。
3.3 不同深度缺陷的气瓶爆破压力的预测
基于3.2 节对含深度为2.1 mm 缺陷的纤维全缠绕气瓶爆破压力的计算方法,对其余缺陷深度分别为0.42、0.84、1.26、1.68 mm 的气瓶进行强度失效预测。在125 MPa 内压作用下,对比完整结构的气瓶和含不同缺陷深度的气瓶的缠绕层,分别讨论两者的1 至10 层的最大轴向和周向应力变化。
由图9可知,含缺陷的复合材料环向层和螺旋层的轴向应力均明显大于不含缺陷的缠绕层,且随缺陷深度增加,轴向应力水平也相应提高。同一缺陷气瓶,缺陷交界处的含缺陷部分的轴向应力明显降低,缺陷部分的环向层的轴向应力水平低于不含缺陷部分环向层的应力水平。由图10可见,含缺陷结构气瓶的环向层和螺旋层的周向应力均低于不含缺陷气瓶,缺陷交界处的含缺陷部分的周向应力明显降低,缺陷部分螺旋层的周向应力水平低于不含缺陷部分螺旋层的应力水平。
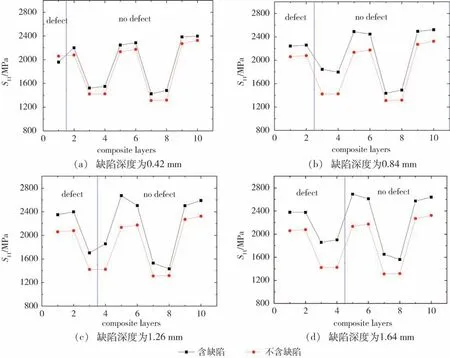
图9 不同缺陷气瓶逐层轴向应力的变化Fig.9 Axial stress of each layer of composite cylinders with different defects
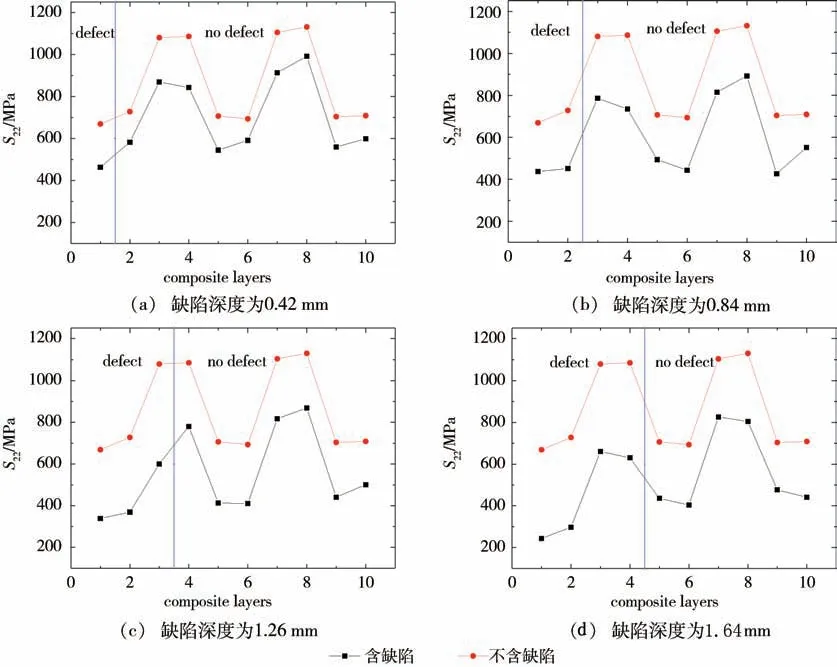
图10 不同缺陷气瓶逐层周向应力的变化Fig.10 Circumferential stress of each layer of composite cylinders with different defects
采用3.2 节相同方法得到下承载能力下降系数φ,将φ 代入式(8)和式(9)中,得到不同缺陷气瓶的爆破压力,见表6。
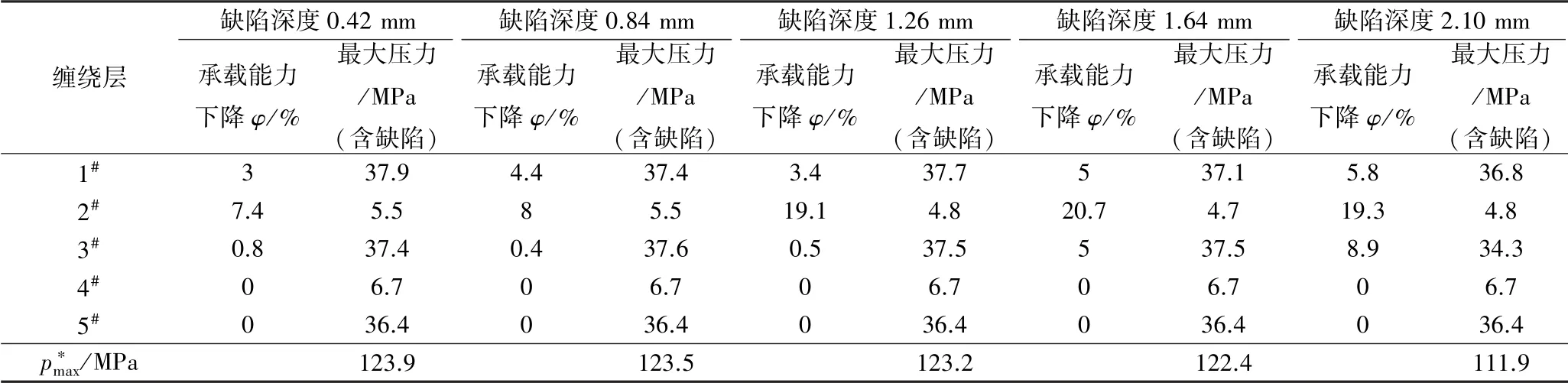
表6 含不同缺陷深度的复合材料圆筒的最大压力Tab.6 Maximum pressure of composite cylinders with different defects
由表6可知,随缺陷深度的增加,缠绕层的承载能力逐层下降,当缺陷深度为(0.42~0.84 mm)时,缺陷主要影响的是第1 层环向层的承载能力;当缺陷深度为(1.26~1.64 mm)时,缺陷主要影响的是第1 层环向层和第2 层螺旋层的承载能力;当缺陷深度为2.1 mm 时,第3 层环向层的承载能力开始受到影响,易发现,环向层出现缺陷对于气瓶承载能力的影响大于螺旋层出现缺陷对于气瓶承载能力的影响。
由图11可知,随缺陷深度增加,纤维全缠绕气瓶的爆破压力不断降低,当缺陷深度小于1.26 mm 时,爆破压力下降的速度相对较小,趋势较为平缓;当缺陷深度大于1.26 mm 时,爆破压力下降的速度迅速增大,影响正常使用。以上结论符合GB24162—2009[9]的要求。
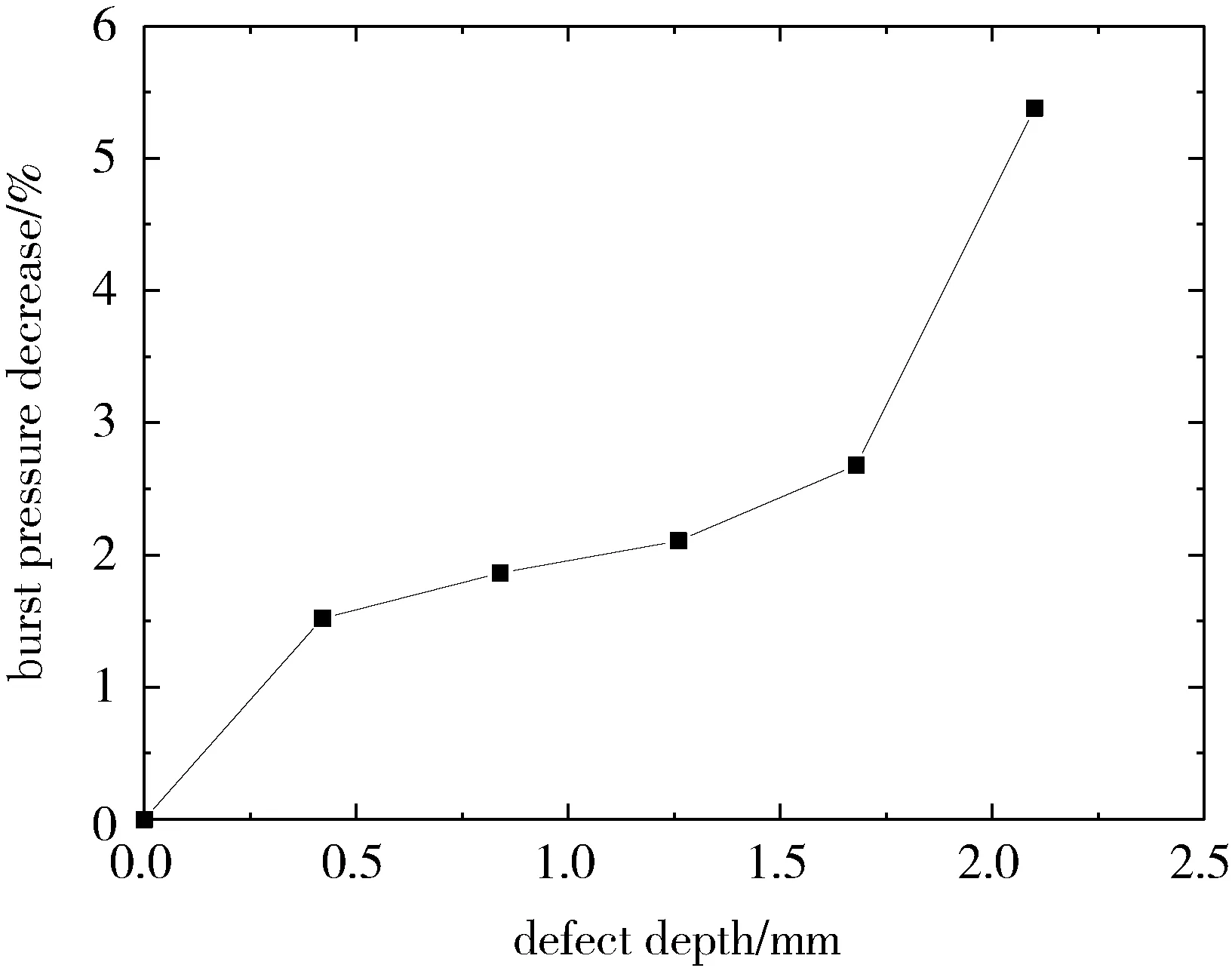
图11 含不同缺陷深度的纤维全缠绕气瓶的爆破压力下降程度Fig.11 Burst pressure decrease of composite cylinders with different defects
4 结论
(1)在内压作用下,外表面含缺陷的缠绕层应力明显高于不含缺陷的缠绕层应力,缺陷处出现应力集中。内衬层和缠绕层在缺陷处均出现不同程度的鼓包变形。
(2)含深度为2.1 mm 的缺陷气瓶,轴向应力随内压变大而大幅增加,而周向应力随内压增加先变大后稳定,爆破压力为130 MPa。
(3)以缺陷深度为2.1 mm 的气瓶为例,基于缺陷对于各层缠绕层轴向及周向应力的影响,以下降系数Φ 表征缺陷对各层缠绕层承载能力的削弱作用,计算出该缺陷气瓶的爆破压力,并与有限元结果相互验证,说明了含缺陷纤维全缠绕气瓶爆破压力计算公式修正方法的正确性。
(4)对含不同缺陷深度(0.42、0.84、1.26、1.64 mm)气瓶的失效强度进行预测,研究发现:随着缺陷深度增加,纤维全缠绕气瓶的爆破压力不断减小,当缺陷深度大于1.26 mm 时,爆破压力下降的速度迅速增大。该结论符合GB24162—2009《汽车用压缩天然气金属内胆纤维环缠绕气瓶定期检验与评定》的要求。

