基于数据的多目标作业车间的复杂网络模型关键节点的寻找
韩佳蓉
(齐鲁工业大学(山东省科学院)计算机科学与技术学院,济南250353)
0 引 言
近年来,生产过程日渐复杂、精细,产生的数据量越来越多,这就使得处理难度也随即增加,如此规模的数据量使生产的细节趋于量化与可控,并能为生产过程的分析提供丰富的资源[1]。作为制造过程优化中至关重要的一部分,多目标柔性作业车间生产问题因在提高生产效率、降低生产成本等方面发挥强大作用而受到大多数企业学者的关注和重视[2]。但传统流程工业模型优化受到发展的限制,面临着更为复杂的情形,研究者为寻求突破便利用复杂网络建模,将生产数据作为模型节点,从多目标制造的数据特征出发,对数据展开深入分析。有关复杂网络的建模方法有:文献[3]探讨了适应性供应链的概念,指出学习是提高供应链适应能力的一个重要途径,提出了适应性供应链的一个初步模型框架。然后建立了供应链的复杂网络演化模型,导出了其基本统计规律。文献[4]将统计方法、非线性系统理论、控制理论以及矩阵理论等理论和方法应用到复杂网络的研究中,对复杂网络的动力学性质和加权复杂网络的建模两个方面进行了研究。而文献[5]中,结合复杂网络理论在复杂系统评价上的优势,运用统计物理、图论、运筹学及计算机模拟等方法,将实际网络特性与复杂网络理论进行关联,建立复杂产品制造过程网络演化模型,从而将复杂网络成功应用于智能制造,且为后续工作增加了一个新的研究思路。
综合前文所述,本文设计了一个基于生产数据信息的多目标作业车间复杂网络模型,该模型以车间实际运转过程中产生的数据作为模型的节点,数据间关系作为复杂网络的边,关系之间权重利用线性函数公式求出。而后利用模糊网络分析法(FANP)求出关键节点,该方法是网络分析法在不确定性和含糊性问题上的延伸,是一种能将2种特性复杂问题的定量化方法。最后进行仿真分析,证明该方法的有效性和合理性,进而表明这是能够适用于多目标作业车间复杂网络模型。
1 多目标作业车间复杂网络模型的搭建
多目标车间作业的复杂网络模型搭建需要经过数据预处理、建立边、确定权重等关键研究步骤。本文用G=(R,E,W)来表示该复杂网络模型,其中R表示节点集合,E表示边的集合,W表示权重集合,这是一个有向加权的网络。本文将给出研究论述如下。
1.1 数据预处理
生产中的数据直接来源于分布于车间各个生产单元中的传感器,例如温度传感器、压力传感器、速度传感器等,按照设定的参数,传感器每隔一段时间便返回当前数据到服务器。由于实际传输过程中传感器无响应导致数据丢失,由传感器信号失真导致的数据错误和异常是不可避免的,为此就要对数据进行预处理:将传感器传回来的一串数据作为一个按时间排列的数据序列,序列的第一个数据编号为0,每个序列的第一个数据不能为空。某一时刻的某序列值为null(传感器未响应请求或捕获数据失败),则所有序列在这一时刻数据重写为null。接下来根据序列生成逻辑序列:开始处理的第一个数据所处的时刻为0时刻,该时刻对应逻辑序列值为0。从第二个数字开始,若数据序列中与前一个数据相比增加了,则逻辑序列生成的数值记为1,不变为0,减小为-1。若遇到null数据,该数据与下一条数据不生成逻辑序列项,从第三条开始重复执行上述规则,直至遍历完整个数据序列。
在预处理阶段会出现2种特殊节点。一类是持续恒增的数据,另一类是恒定不变的数据。恒定不变的数据记为N/A(not available),不参与后续边的建立和边权的设置;持续增量数据生成增量阵列IQA(Incremental Quantity Array),IQA 生成时处理null类数据与正常序列相同,记录与上一条数据相比数据增值量。根据IQA生成逻辑序列,求出IQA中的众数,并将IQA中的每个数据与之比较后生成逻辑序列,若大于该值记为1,等于记为0,小于记为-1。
1.2 复杂网络模型的建立
在基于数据的复杂网络模型中,模型的节点R不再是具体的某个生产环节,而是不断产生数据序列的数据点集合。数据节点与工序间的关系如图1所示,由图1中可以看出一个流程实体包含了多个数据。
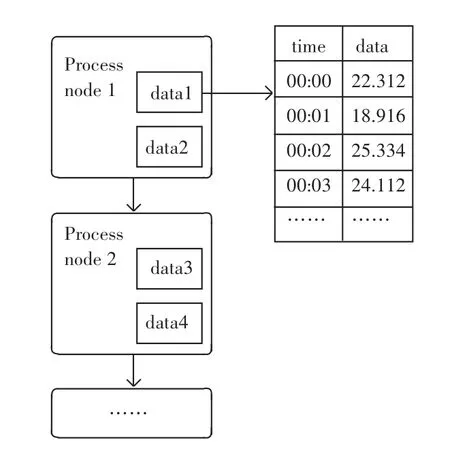
图1 工序与节点表示图Fig.1 Process and node diagram
在数据预处理阶段,本文已将数据处理作为逻辑序列,在此基础上即利用Apriori算法挖掘这些逻辑序列之间的关系。设定存在A,B两个节点,若A,B同增、同减用A→B表示;A增大、B减小,或A减小、B增大时用A→-B表示;2个节点不存在关联用A→┐B表示。节点A,B之间的关系,只有A→B、A→-B以及A→┐B三种情况事件,则所有事件逻辑表示及概率见表1。

表1 所有事件逻辑表示及概率表示Tab.1 All practical logical representations and probabilistic representations
综合上述分析,就能得到每个事件的支持度计算公式可表示为:

当ξ=0 时,P(others)=P(1,0)+P(0,1)+P(0,-1)+P(-1,0)+ξ,若P(others) 的值大于或等于 30%(节点A、B间不存在关联),计算c(others)=1/3(c(1,0)+c(0,1||-1)+c(-1,0))的值,其值大于44%则认定A、B之间没有关联。若P(others)不满足最小支持度或最小置信度,则A、B之间可能存在关联,验证当ξ=0时P(A∪B)和P(A∪-B)的值,若其值大于40%,则A,B之间存在关联。当确定A、B存在何种关联后,研究推得对应的置信度的数学公式如下:

若2个节点最小支持度为40%且满足最小置信度为60%,则这2个节点间存在强关联规则,在A、B两节点之间建立边。若不满足最小支持度40%或不满足最小置信度60%,则A、B之间不存在强关联规则,不在A、B之间建立边。
为了准确地描述数据之间的关系,需要在模型中为每一条边加入权重。边的权重集可表示为W={wij=f(ri,rj)|i,j∈ (1,2,3,…,r)},其中,wij表示从节点i指向节点j的边的权重。若A,B两节点是有关联的,则上游节点产生的数据和下游节点产生的数据间将存在一定的函数关系。设节点ri与rj为节点集r中2个相邻的节点,边的方向由ri指向rj,则在某一时刻节点ri与rj的值存在函数关系rj=f(ri),该函数表达式可由节点ni与节点nj的数据序列求得。 那么ri,rj之间的权值可表示为Wij=f'(ri)。 当且仅当两节点间为线性变化关系时,权值Wij才为常数。不难理解,在实际生产过程中,该函数关系并不总是线性的,因此在很多情况下,该值是变化的。研究中假设当节点ri的值为x时,节点rj的值为y,则权值Wij的数学表述如下:
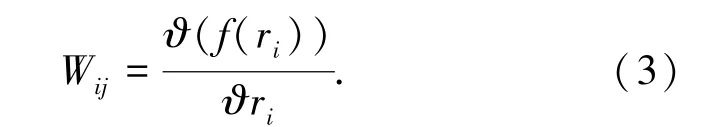
当两点间的关系为非线性关系时,得到的权值将是一个函数值随上游节点数据变动的函数表达式,反映了上游节点对下游节点影响力的大小。由此可以构建一个基于数据的有向加权复杂网络模型。
2 模糊网络分析法
模糊网络分析法是基于网络分析法与模糊集理论相结合的一种系统决策方法[6]。对此可做探讨分述如下。
2.1 三角模糊数
模糊数的模糊集合可以表示为F={x∈R:-∞<x<+∞,μF(x)是从R到区间[0,1]上的一个连续的映射。三角模糊数M常用(l,m,s) 来表示,即M=(l,m,s),其中l≤m≤s。三角模糊数M的隶属函数fM(x):R→ [0,1], 如图2所示,进而推得其数学定义可写作如下形式:
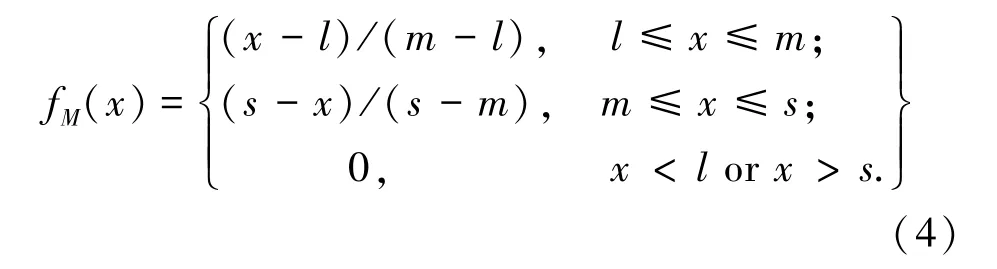
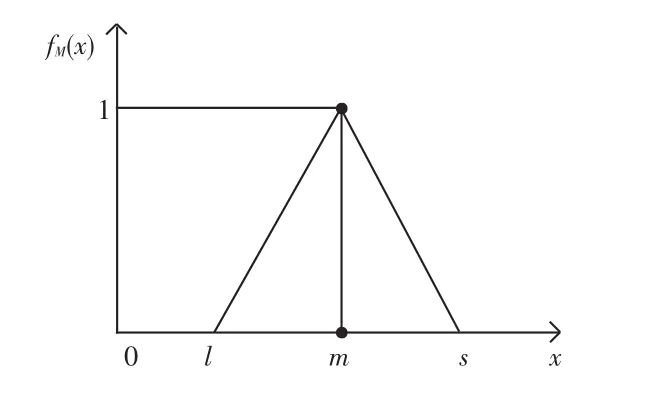
图2 三角模糊数MFig.2 Triangular fuzzy number M
其中,l和s分别表示为M评价小组所确定的下界和上界最小最大值,m为隶属度最可能值。s-l越大、越模糊;s-l越小、模糊度越低,l=m=s时说明判断是非模糊的,三角模糊数的取值参见表2。

表2 重要程度定量表Tab.2 Quantitative table of importance
2.2 模糊网络分析法基本步骤
首先确定复杂网络关键节点的评语集以及评价因素集:评判者要对评判对象做出各种可能的评判结果, 这些结果组成一个集合V={V1,V2,....,Vm}。 复杂网络的因素集U={U1,U2,....,UN} ,其中Ui={Ui1,Ui2,...,Uin},(i=1,2,....,N)。获得对复杂网络的指标进行单因素评价,建立U到V的模糊关系F×R,下一步即需求得FANP的权重。在本文中,ANP模型分为控制层和网络层两个部分,如图3所示。由图3可知,控制层是一级指标、即设备自身属性和网络特征参数,U1包括设备价值、生产能力、故障频率、维修费用;网络层是二级指标,二级指标U2包括度、介数、聚类系数、节点特征向量。此后,就是研究运算得到复杂网络关键节点评价的各个指标权重,利用各个指标权重带入实际节点的真实数据,最终得到排名靠前的节点为关键节点。研究中,各步骤设计内容可详述如下。
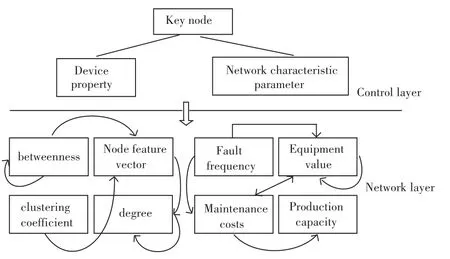
图3 ANP结构模型Fig.3 ANP structure model
(1)应用三角模糊数构造模糊判断矩阵。假设节点组U1中某一节点U1i(i=1,2,....,n) 对复杂网络关键节点的影响程度为次准则,运用三角模糊数的性质来构造U1中各个节点间两两互补判断矩阵,记pij=(lij,mij,sij),共有n个。 对任意的pij、pji都有lji+sij=mji+mij=sji+lij=1。
(2)确定超矩阵的局部权重向量W11及其它。W11是一个矩阵,这是U1中的某一节点U1i(i=1,2,..,n)对复杂网络关键节点影响程度的次准则,判断U1中各个节点两两相比较的重要性。对其设计过程可阐述如下。
Step1 计算节点U1i的综合重要程度C1i,研究推得的计算公式为:

其中,C1i是三角模糊数,可以表示为C1i=(,,),(i,j=1,2,..,n)。 研究中还将用到的其它计算公式见如下:
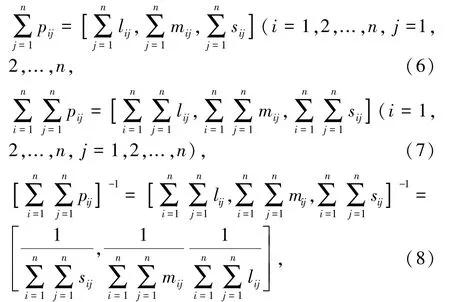
Step 2计算C1i≥C1k的可能程度,其计算公式为:
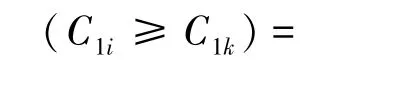

其中,i=1,2,..,n,k=1,2,..,n&k≠i,j=1,2,..,n。
Step 3计算U1中的节点U1i(i=1,2,..,n) 相对于其它节点的可能性重要程度,具体公式如下:
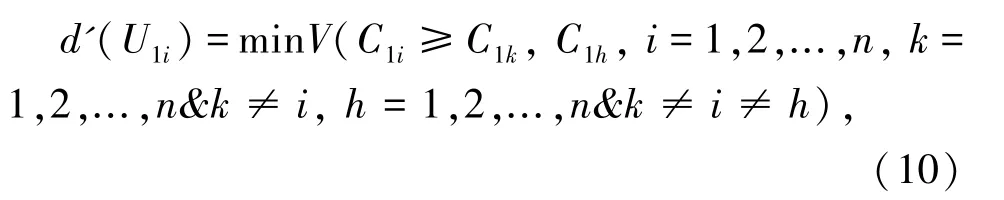
Step 4重复Step1~Step3n次,可以得到权重向量。这个过程中得到了n个d′(u1i),继而得到d'(U1n))T,然后将其归一化就可以得到权重向量(d(u11),d(u12),..,d(u1i),..,d(u1n))T。
Step 5重复Step1~Step4n次就可以得到n个,获得超矩阵局部权重向量W11,即:W11=
(3)计算Wij(i,j=1,2,..,N)。 以节点组Ui中各个节点对复杂网络关键节点的影响程度为次准则,将Uj中的节点两两比较或者模糊判断矩阵并且进行一致性检验,再用相同计算得出Wij(i≠j)。
(4)确定复杂网络关键节点的超矩阵W和加权超矩阵,加权超矩阵可根据式(11)计算得到,即:
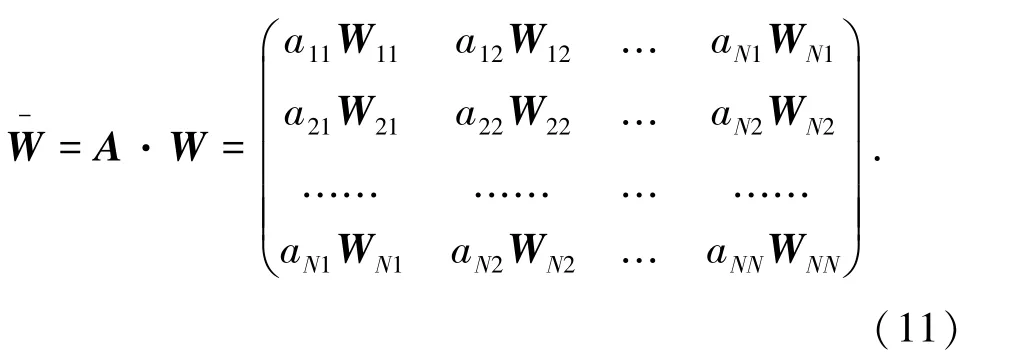
(5)确定FANP的权重Q。 FANP的权重Q是极限超矩阵的列详细,利用Matlab计算出,便可确定权重向量。
3 仿真实验分析
3.1 复杂网络模型的搭建
本文以某无碱窑炉工艺生产玻璃纤维的加工流程为实例,其中的无碱窑炉工艺生产玻璃纤维的加工流程如图4所示。该生产流程包括12个不同环节,总共有139个数据传感器接收点。选取一条生产线的数据,利用本文提出的方法建立基于数据的复杂网络模型,其可视化效果如图5所示。由图5可以见到,图中包含了部分孤立节点,这些节点中有一些是监控型节点,这是由节点属性导致。在该模型中,边反映了是否存在关联,边的权重代表了数据之间存在何种关联。利用复杂网络相关公式计算出不同节点的度、介数、聚类系数和节点特征向量。计算结果见表3,由于计算数据较多,文中仅节选了部分数据。

表3 复杂网络评价指标和重要度Tab.3 Evaluation indicators and importance of complex networks
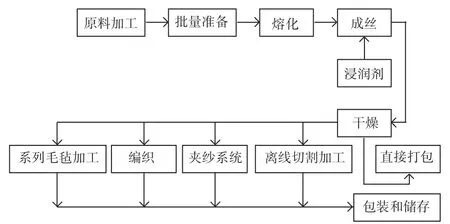
图4 玻璃纤维生产过程任务流程图Fig.4 Task flow chart of fiberglass production process
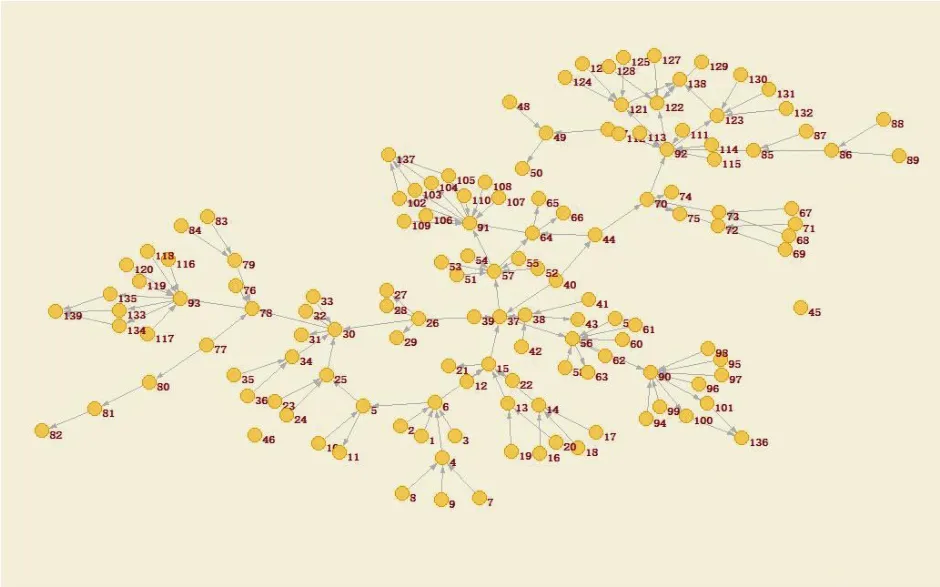
图5 基于数据的复杂网络模型图Fig.5 Data-based complex network model diagram
依据重要度评价体系中的评价属性对传感器所监测机器的设备价值、产能、故障频率、维修成本等数据收集汇总后进行归一化处理,处理结果见表4。由于数据较多,也只列举了其中一部分。
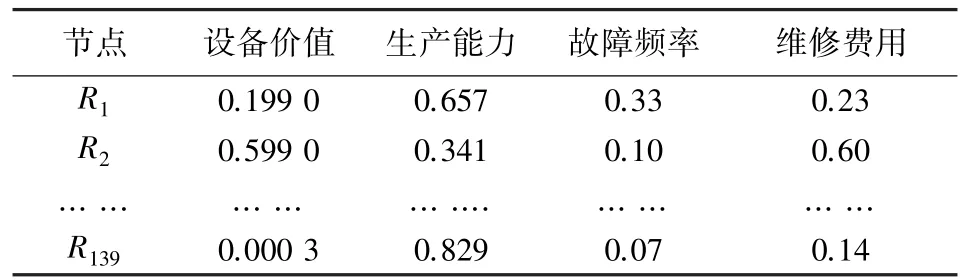
表4 资源节点本身属性Tab.4 The attributes of resource node
3.2 复杂网络关键节点评价
为了模型描述的方便与精确起见,研究中把评价目标评语分为4个等级,分别是:V={非常重要、较重要、较不重要、不重要},一级指标因素集U={U1,U2}={设备自身属性,网络特征参数},二级指标因素集U1={U11,U12,U13,U14}={设备价值,生产能力,故障频率,维修费用};U2={U21,U22,U23,U24}={度,介数,聚类系数,节点特征向量}。选择智能制造领域专家、一线人员、工厂管理人员等对二级指标进行单因素评判,获得二级指标评判结果,详见表5。
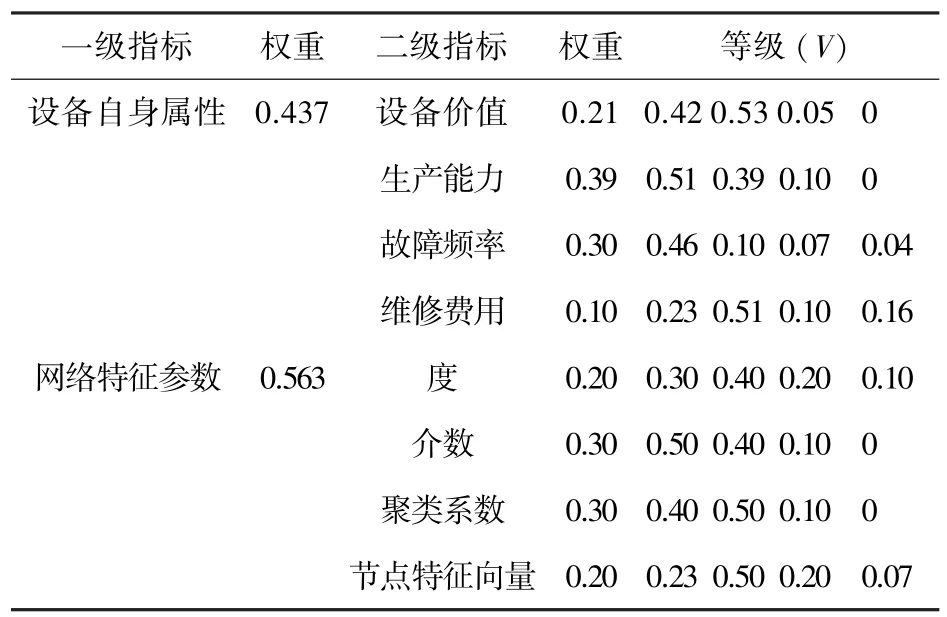
表5 各指标的模糊权重集Tab.5 Fuzzy weight set of indicators
利用表5拟将进行模糊综合评判,得到F×R。考虑到篇幅有限,故而文中省略了此后各步骤的运算结果。而在将得到的指标综合评价系数与各个节点相应的实际数据实现有机结合后,则逐个进行运算,最终得到排名靠前的节点,即为所求关键节点,完整序列对比输出见表6。 该结果与传统的AHP层次分析法相比较,模糊网络分析法修正了AHP层次分析法的主观性和含糊性,识别度更高,识别结果更加准确。

表6 节点重要性排序结果Tab.6 Node importance sorting results
4 结束语
本文利用数据信息通过Apriori算法挖掘数据关系,搭建了一个多目标作业车间复杂网络模型,该方法通过复杂网络的形式将生产中的数据组织起来,最大程度地利用了车间加工过程中产生的数据资源。在此模型基础上,又利用模糊网络分析法寻找该模型的关键节点,用实例证明该方法比传统的AHP层次分析法找到的关键节点更为准确,识别度更高,并且能成功应用于基于数据的复杂网络模型。

