RSSI测距在蓝牙室内定位抗差算法中的应用

王 乐，刘万青，黄观文，张菊清

(长安大学地质工程与测绘学院，西安 710000)

0 引言

随着时代进步，用户对定位服务需求越来越高。目前，全球卫星导航系统(Global Navigation Satellite System，GNSS)技术应用广泛，可满足用户室外定位需求。但是，在室内环境下，受建筑物遮挡，卫星信号衰减极大，无法进行室内定位[1]。而人们处于室内的时间超过80%。因此，研究室内定位技术具有较大意义。常用的室内定位技术主要包括超带宽(Ultra Wide Band，UWB)、超声波、射频频率识别(Radio Frequency Identification，RFID)、ZigBee、红外线、WiFi、蓝牙等[2]。其中，UWB和超声波技术硬件成本高，RFID和ZigBee技术需要额外设备辅助定位，红外线穿透力较差，WiFi信号波动较大，蓝牙信号易受干扰[3]。由于蓝牙设备具有低功耗和低成本的特点，且部署方案简单，目前已被广泛应用于室内定位，且最新发布的蓝牙5.1增加侧向功能，可以为进一步提高定位精度提供更多的观测信息。

目前蓝牙定位技术主要基于接收信号强度指示(Received Signal Strength Indication，RSSI)。基于RSSI定位包括测距和非测距两种方法[4]。相对于非测距法，测距法算法简单、工作量小。测距法的实质是通过求得在当前环境下信号强度与距离的关系式，由信号强度求出观测距离，根据距离定位的方法求出待定点坐标。蓝牙信号传播过程中，人员扰动、房间障碍物等会对信号产生干扰。因此，部分学者对基于RSSI测距的室内定位方法进行了深入研究，提出了相关解决办法。杨文铂等通过构建自适应测距模型以削弱实际环境下由于不确定因素引起的测距误差[5]。石为人等建立了空间补偿模型，以削弱待定点与信号发射设备不在同一平面上所带来的测距误差[6]。吴君钦等采用高斯滤波的方式对RSSI数据进行处理以削弱环境因素引起的RSSI扰动影响[7]。罗宇锋等在定位方法方面，采用消除高度影响的加权质心定位算法来计算目标点位置[8]。

为提高基于RSSI测距的蓝牙室内定位的抗差性和可靠性[9]，本文基于抗差思想和三边定位原理，将人员扰动等引起的信号强度变化所带来的测距误差视为异常误差，提出了基于RSSI测距的蓝牙室内定位抗差算法，建立了相应的抗差模型，并采用了四种不同抗差算法进行定位计算，统计、比较和分析了其定位效果，为蓝牙室内定位抗干扰算法提供了理论和应用参考。

1 基于RSSI测距的蓝牙室内定位原理

本文采用的基于RSSI测距的蓝牙信号传播模型[10]可简写为

RSSI=A-10n·lg(d)

(1)

式中，RSSI表示接收信号强度；A表示距离蓝牙信号1m处的信号强度；n表示路径损耗因子，即特定环境下的衰减速率，它的大小与天气、湿度等环境有关，可通过经验值或根据实际环境测算以获取环境变量[11]；d表示接收端与蓝牙信号之间的距离。具体计算方法本文不再赘述。

边长计算公式可写为

(xs-xi)2+(ys-yi)2=di2

(2)

式中，(xs,ys)表示待求点坐标；(xi,yi)表示第i个蓝牙发射装置的位置坐标，其中i=1,2，…，m；di表示第i个蓝牙发射装置与待测点的平面距离。

利用最小二乘原理可解得

(3)

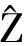
其中

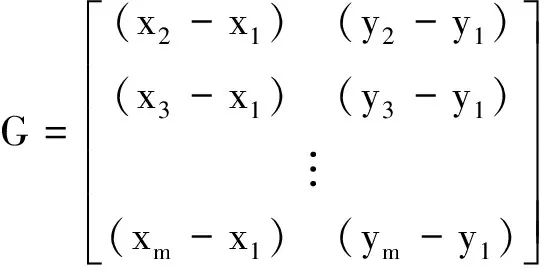
2 基于RSSI测距的蓝牙室内定位抗差算法

基于RSSI测距的蓝牙室内定位时，受人员扰动等影响，蓝牙信号会发生多次折射，造成测量误差。本文将信号强度变化引起的距离观测误差视为一种异常误差，采用常用的几种抗差估计算法，尽量减少粗差影响，得到最佳估值[12]。

选权迭代法是通过降低含异常观测值的权以抵制和削弱异常值对定位精度影响的方法，其计算模型如下。

首先，由式(3)得观测值改正数为

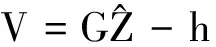
(4)

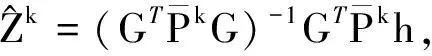
2.1 胡贝尔法

胡贝尔法权函数为

(5)

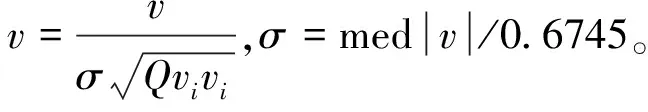
由式(5)可以看出，当改正数v的绝对值小于等于c时，即为经典的最小二乘估计；当改正数v的绝对值大于c时，即进行降权处理，改正数越大权越小。

2.2 汉佩尔法

汉佩尔法权函数采用四段式

(6)

式中，a=1.7σ,b=3.4σ,c=8.5σ。

2.3 IGG法

IGG法是由中国科学院测量与地球物理研究所周文江教授最初提出的[12]，其权函数公式如下

(7)

式中，C表示相对|v|的一个很小的量。

2.4 多维粗差同时定位定值法(LEGE法)

除上述抗差算法外，还可以采用多维粗差同时定位定值法以提高定位精度。

根据最小二乘平差可知[18]

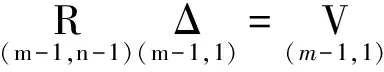
(8)

式中，R=G(GTPG)-1GTP，表示平差因子；Δ表示真误差，V表示改正数向量。

假设Δ中存在g个粗差，设Δ1为粗差值，则有

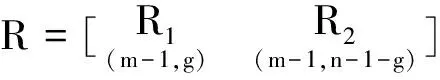
式(8)可写为

R1Δ1+R2Δ2=V

(9)

通常R1Δ1对改正数V的影响远远大于R2Δ2，因此有

R1Δ1≈V

(10)

进而可得

(11)

利用该值对观测值进行修正后，再采用最小二乘法求解最优待估参数。

然而在实际解算过程中，粗差位置和个数均未知，因此需要通过逐阶搜索的方法，从1阶开始逐阶搜索至r-1阶。在逐阶搜索过程中，若探测到疑似粗差，则停止搜索。判断的标准为

(12)

若式(12)成立，则停止搜索，可判定存有k个异常信号，否则继续搜索。

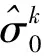
3 实验设计与结果分析

为对上述算法进行验证分析，本文设计了基于RSSI测距的蓝牙室内定位抗差试验。选取的试验地点为某大厦走廊内，设备布设如图1所示，在走廊里安置10个蓝牙，编号分别为1～10，S1、S2和S3为待估点，各点分别采集蓝牙信号60次。

图1 场景布设情况Fig.1 Layout of the scene

本文设计了两种试验方案如下。

方案1：无人员扰动情况下进行数据采集。

方案2：试验人员在场所随机走动情况下进行数据采集。

首先，在设备布设的走廊里每隔1m进行蓝牙数据采集，计算出参数A和n。

然后，分别采用最小二乘法、胡贝尔法、汉佩尔法、IGG法和LEGE法五种方法对方案1和方案2的待定点坐标进行计算。

具体统计结果如表1、图2和图3所示。

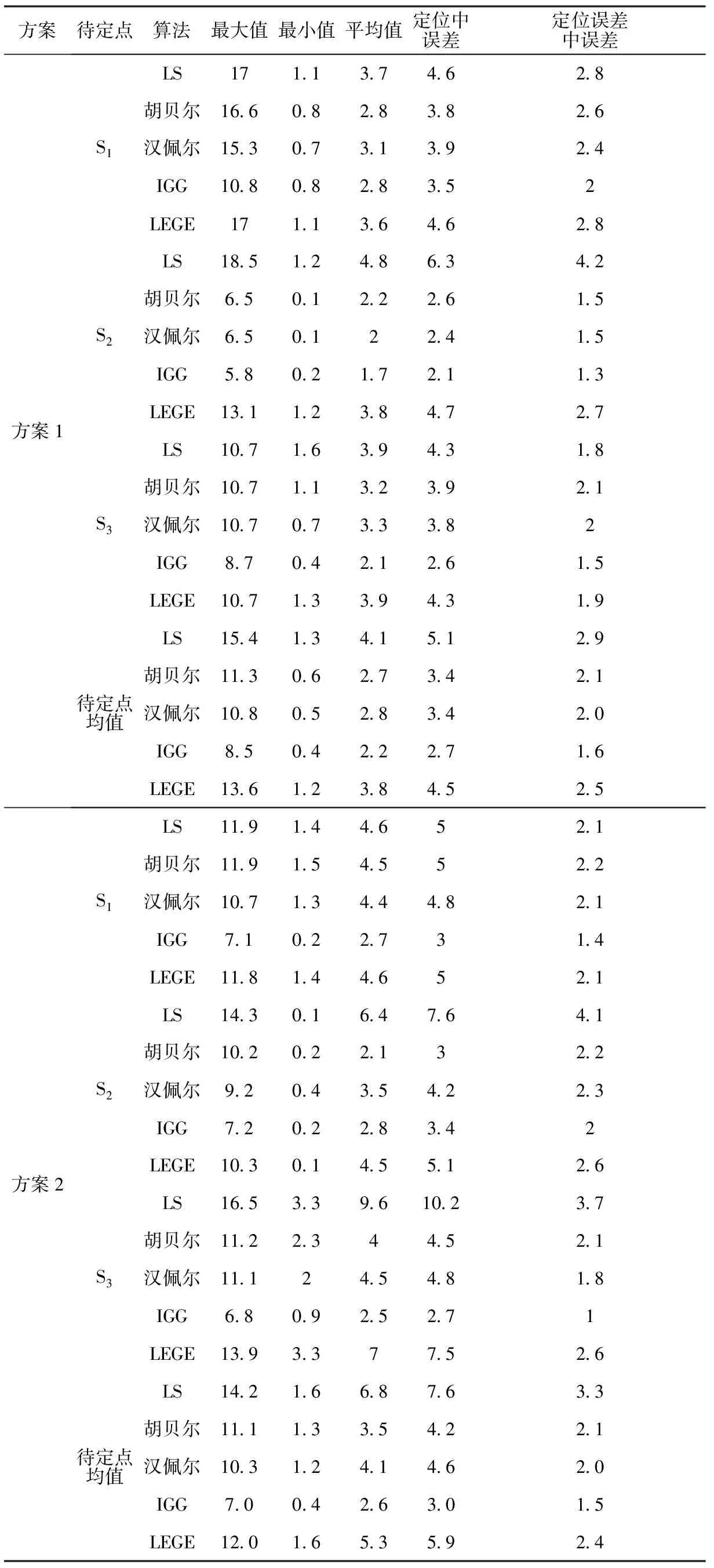
表1 不同方案和方法定位误差统计

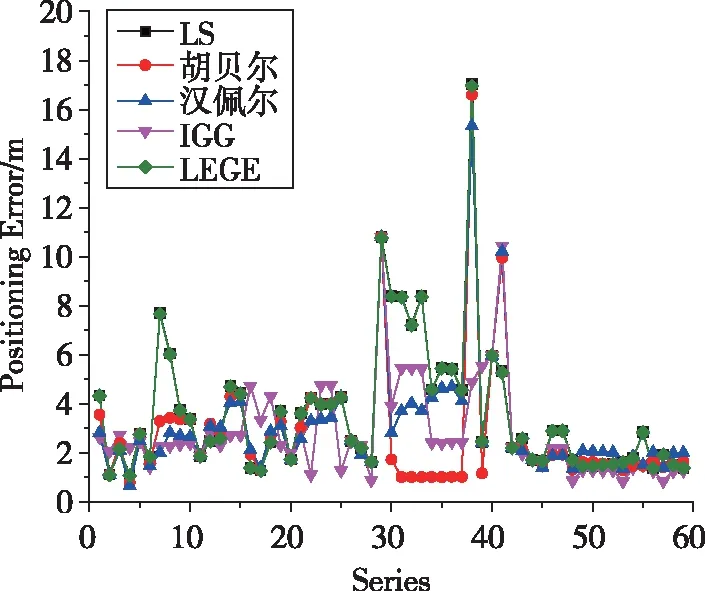
(a)S1点的结果

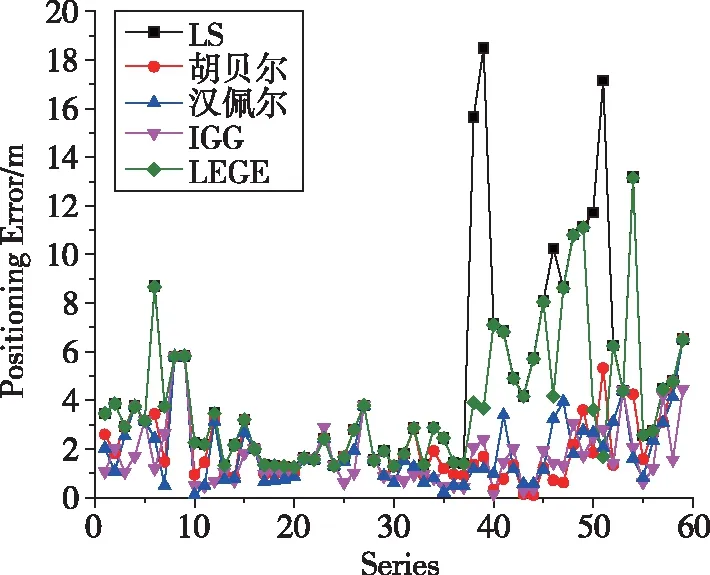
(b)S2点的结果

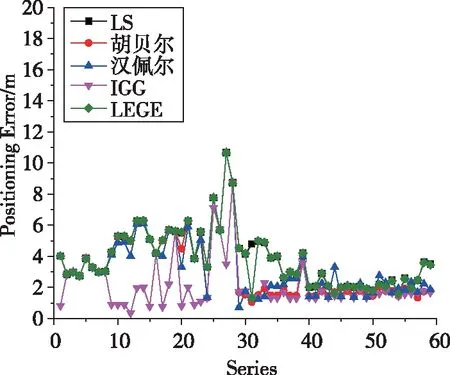
(c)S3点的结果图2 方案1定位误差统计Fig.2 Statistics of positioning error of Scheme 1

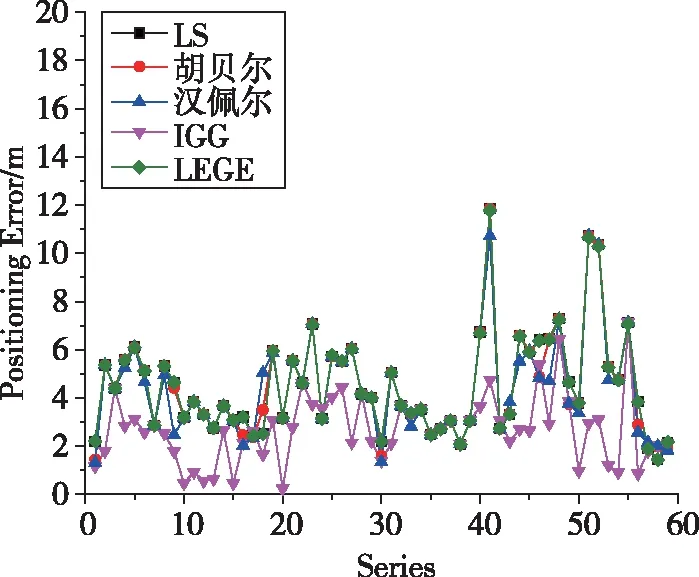
(a)S1点的结果

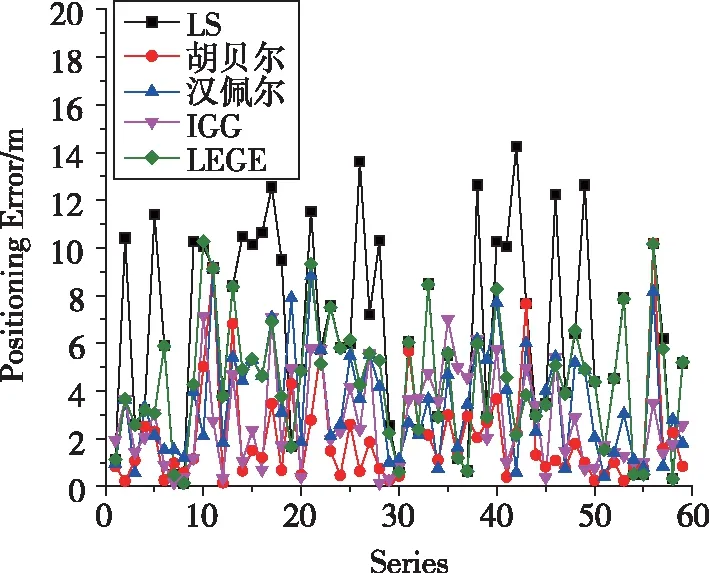
(b)S2点的结果

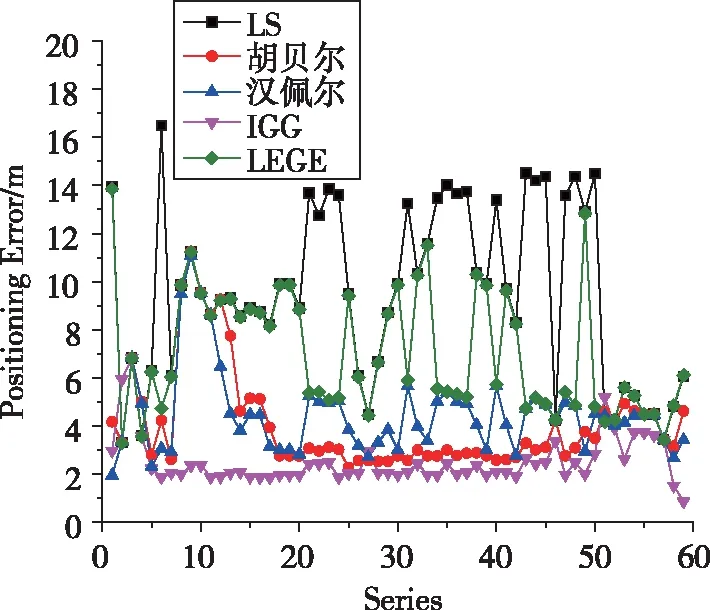
(c)S3点的结果图3 方案2定位误差统计Fig.3 Statistics of positioning error of Scheme 2

通过表1、图2和图3可知：

1)利用最小二乘方法进行定位，不管有无人员扰动，定位精度均较差。原因为蓝牙信号易受环境干扰，而最小二乘法无抗差性。

2)在无人员扰动情况下，相对于最小二乘方法，胡贝尔法、汉佩尔法、IGG法和LEGE法精度分别提高34%、33%、46%和8%。在人员随机扰动情况下，相对于LS法，各抗差法精度分别提高48%、40%、61%和22%。分析原因为抗差算法不同程度地消除了部分异常信号。

3)对比本文采用的抗差方法精度，可知IGG法最优，其次为胡贝尔法，略优于汉佩尔法，LEGE法改善效果相对较差。在有人为干扰情况下，IGG法的平均定位精度约为3m，定位误差中误差优于1.5m。

4)IGG法的定位结果具有较好的稳定性，但是仍然存在部分跳变现象，这可能与蓝牙设备的不稳定性或算法有待进一步优化有一定关系。

4 结论

在实际室内环境中，蓝牙信号强度必然会受到人员扰动等影响，从而导致基于RSSI测距的蓝牙室内定位精度受到较大影响。本文采用了常用的胡贝尔法、汉佩尔法、IGG法和LEGE法，比较了四种不同抗差方法的定位效果。试验结果分析表明，抗差算法对蓝牙室内定位精度均有一定的改善效果，其中IGG法定位精度最高、稳定性最好。因此，利用抗差算法进行基于RSSI测距的蓝牙室内定位具有研究和实际应用意义。