平面分析法在减振器强度校核的应用研究

邢立巍，王孔龙，胡春波，聂小刚，周 凯，张一弘 Xing Liwei，Wang Konglong，Hu Chunbo，Nie Xiaogang，Zhou Kai，Zhang Yihong



平面分析法在减振器强度校核的应用研究

邢立巍1，王孔龙2，胡春波1，聂小刚1，周 凯1，张一弘1Xing Liwei1，Wang Konglong2，Hu Chunbo1，Nie Xiaogang1，Zhou Kai1，Zhang Yihong1

（1.众泰控股集团汽车工程研究院，浙江 杭州 310018；2. 北京北汽德奔汽车技术中心有限公司，北京 101300）

在减振器强度校核方面，采用了平面分析法进行弯扭强度分析，解决了减振器因外筒弯曲变形导致漏油失效的故障，验证了平面分析法在减振器强度校核方面的应用价值。

平面分析法；减振器；强度校核

0 引 言

在汽车悬架的减振器实际工作中，由于车轮的跳动和路面的冲击，减振器的外筒会一直有弯矩作用存在，若减振器的外筒强度不足，会发生弯曲变形，导致减振器漏油失效，并且会导致车轮外倾角变化，造成车辆的操纵稳定性和平顺性下降；因此，对减振器进行可靠的强度校核分析尤为重要。当前普遍做法是利用ADAMS等动力学仿真软件提取悬架系统的各个惯性力，再利用ABAQUS、Nastran、Hyperworks等软件进行处理分析。这种CAE（Computer Aided Engineering，计算机辅助工程）分析校核方法所需参数量较多，在设计开发初期难以提供足够准确的信息，导致计算出来的结果存在较大的差异。

提出一种平面分析法在麦弗逊悬架系统减振器强度校核方面的应用，将汽车悬架的空间结构简化为前轮轴线垂直于车辆前进方向的平面力系，在这个平面内进行校核分析，根据外筒弯曲应力的大小来选择外筒材质和规格。

某车型在道路试验过程中出现减振器漏油现象，经查，该减振器的外筒已变形失效，如图1所示。

该减振器在设计初期利用CAE进行校核仿真满足性能要求，说明在变量参数提供不够全面准确的情况下，进行CAE校核存在一定隐患；因此采用平面分析法进行该减振器弯扭强度的校核。

图1 减振器外筒弯曲变形失效

1 平面分析法校核的基础假设

1.1 前提条件

汽车处于满载状态，保持静止不变，在轮胎接地点施加向上的3.5冲击载荷，减振器的上安装点为球铰；计算中力的单位为N，长度单位为m，应力单位为MPa。

1.2 悬架简化

典型的麦弗逊悬架系统如图2所示，由减振器、下摆臂总成、稳定杆、稳定杆连接杆、副车架、转向节及轮胎等组成。

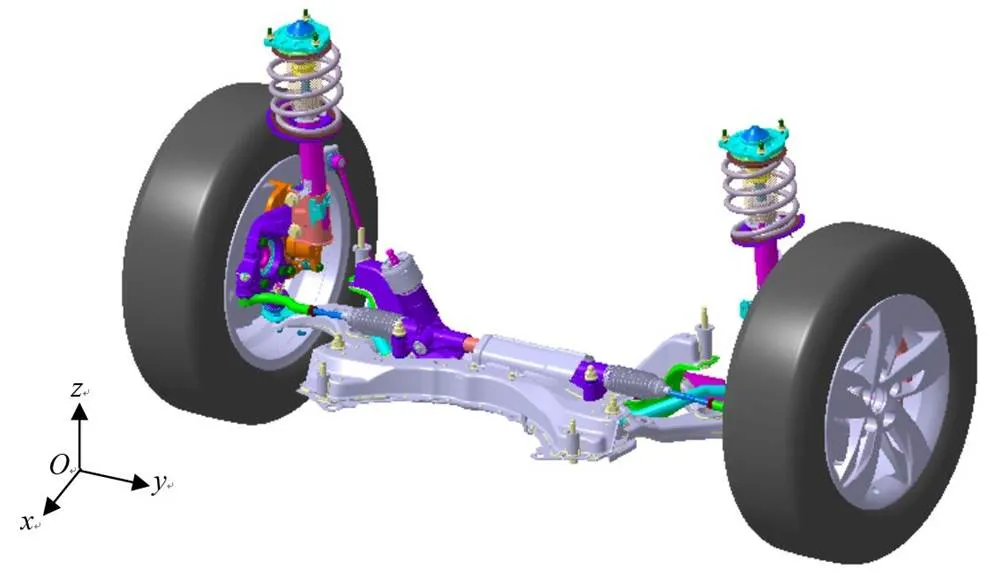
图2 典型的麦弗逊悬架系统

假定转向节与副车架等零部件为刚性部件，减振器由活塞杆和缸筒组成，将麦弗逊悬架系统的空间受力简化为平面杆系结构，如图3所示。

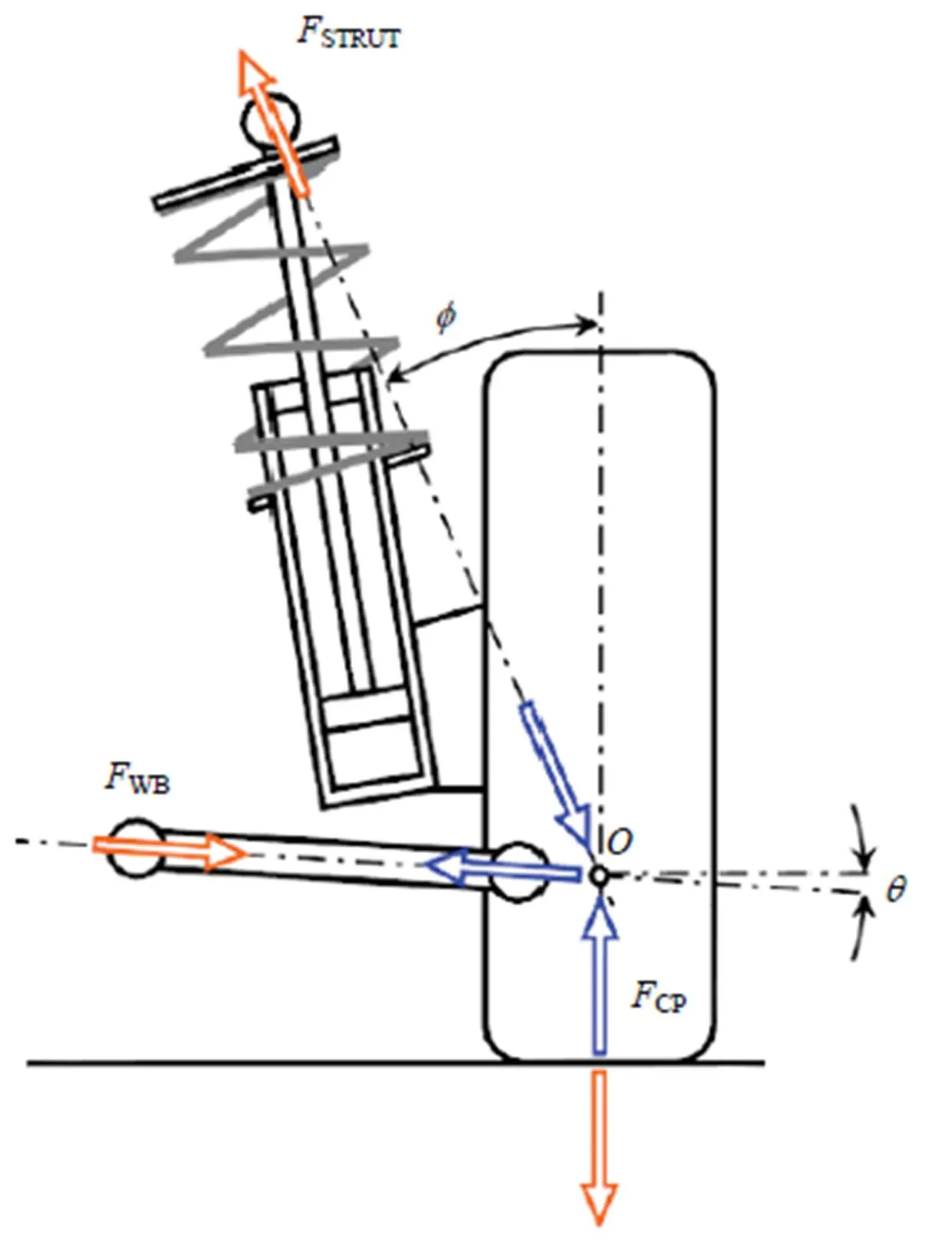
图3 麦弗逊悬架系统平面杆系结构图

2 减振器外筒弯扭强度校核分析

2.1 麦弗逊悬架系统的机构特性

麦弗逊悬架系统的空间自由度为1，即该机构只有1个自由度，具有特定的运动，且每一个运动姿态都是确定的，对应着悬架系统的每一种实际工况。

从结构力学上看，麦弗逊悬架系统是一种空间杆系结构。悬架系统在运动过程中是一个几何可变体系，而在悬架系统的每一种姿态下，由于悬架系统达到了内力平衡，每一个杆件的位置都是确定的，从结构上看也是一个几何结构不变体系；因此，是一种可以进行静力分析的静定结构。

2.2 麦弗逊悬架系统受力分析

在平衡状态下，将麦弗逊悬架系统简化为平面杆系结构，上支座衬套为球铰副，则减振器受力就转化为一个平面内力系平衡的问题。

由理论力学可知，力系平衡的充要条件是力系的主矢和对任一点的主矩为零；另外一种表示形式为：力系中各力在直角坐标系每一坐标轴上的代数和为零，对每一坐标轴主矩的代数和为零。

根据之前假设可以得到：

1）下摆臂、减振器可看成是一个二力杆；

2）减振器受到的侧向力、减振器活塞杆受力以及螺旋弹簧受到的力对整个麦弗逊悬架系统来说，都可以转化为减振器的内力，在进行受力分析时，转向节、轮胎、减振器作为一个整体，在减振器上安装点受力、下摆臂拉力以及地面反力作用下保持静态平衡。

2.3 减振器外筒弯曲应力计算

麦弗逊悬架系统在地面反力CP、下摆臂拉力WE、滑柱上点受力STRUT作用下保持平衡，得到以下各式。

水平方向上力的平衡

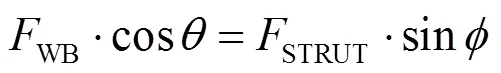
垂直方向上力的平衡

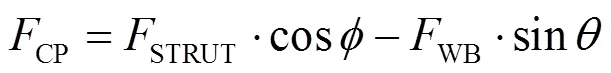
式中：CP为3.5单边满载冲击力，N；为摆臂拉力延线与车轮接地中心面交点与减振器上点的连线与垂线间的夹角，（°）；为摆臂拉力与水平方向的夹角，（°）。

将式（1）带入式（2）得

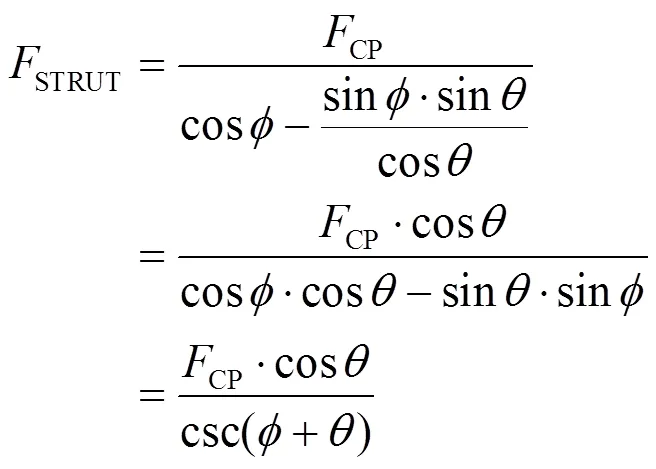
减振器外筒出现弯曲，是由于受到了弯矩作用，如图4所示，受力分解可得减振器上点在垂直于减振器外筒方向的受力为

式中：为摆臂拉力延线与车轮接地中心面交点与减振器上点的连线与减振器外筒间的夹角，（°）。

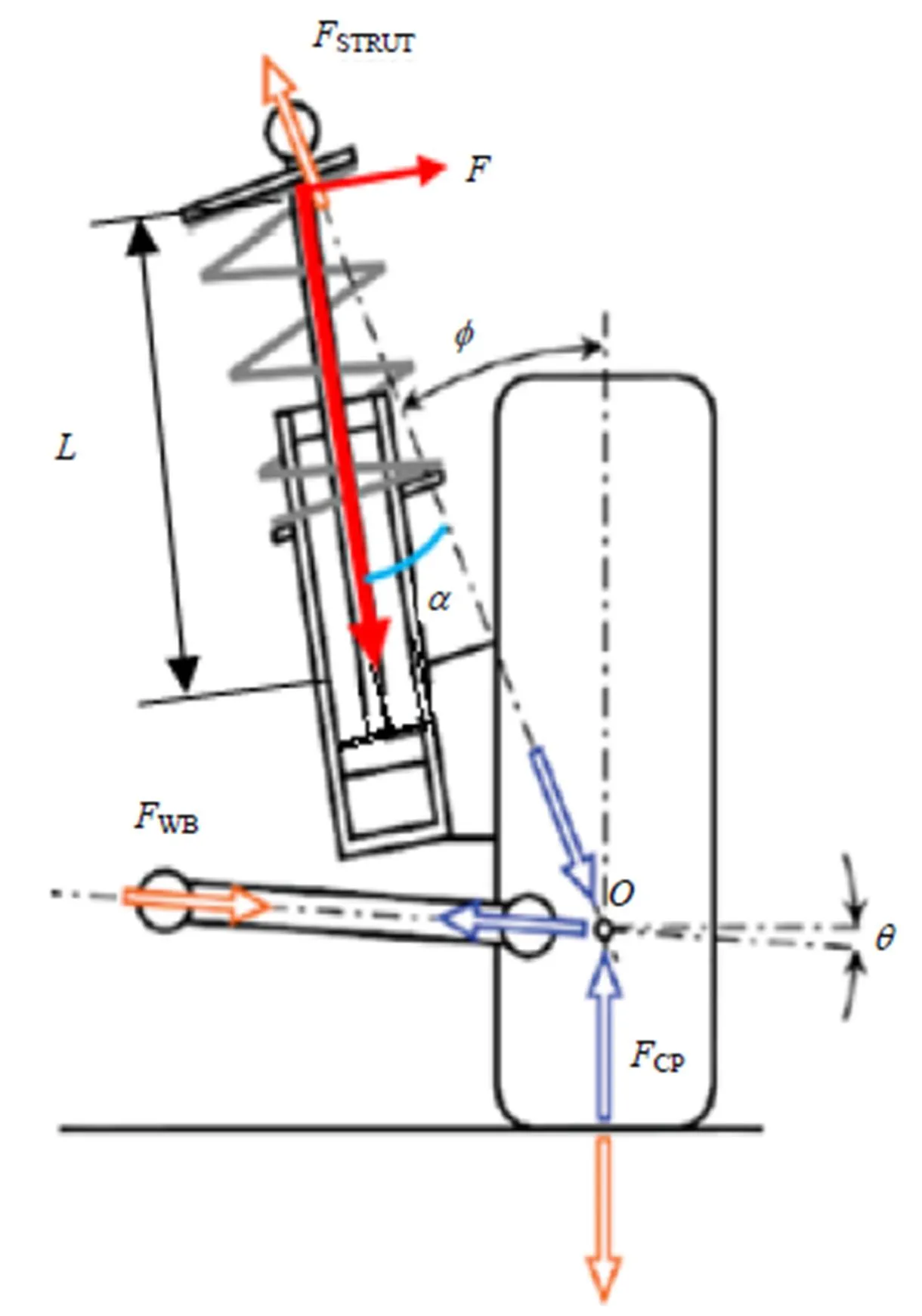
图4 前滑柱受力分解示意图

前滑柱外缸筒受到的弯矩为

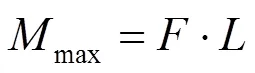
式中：为减振器上点到转向节支架安装点的距离，m。

前滑柱外缸筒抗弯截面系数为[1]142，324

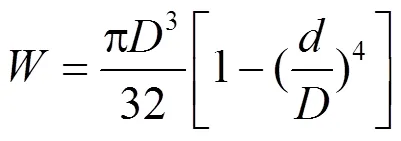
式中：为减振器外缸筒的外径，m；为减振器外缸筒的内径，m。

最大弯曲应力max应不大于材料的屈服强 度[1]142，即

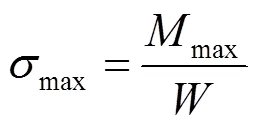
经查，该故障车辆的相关技术参数见表1。

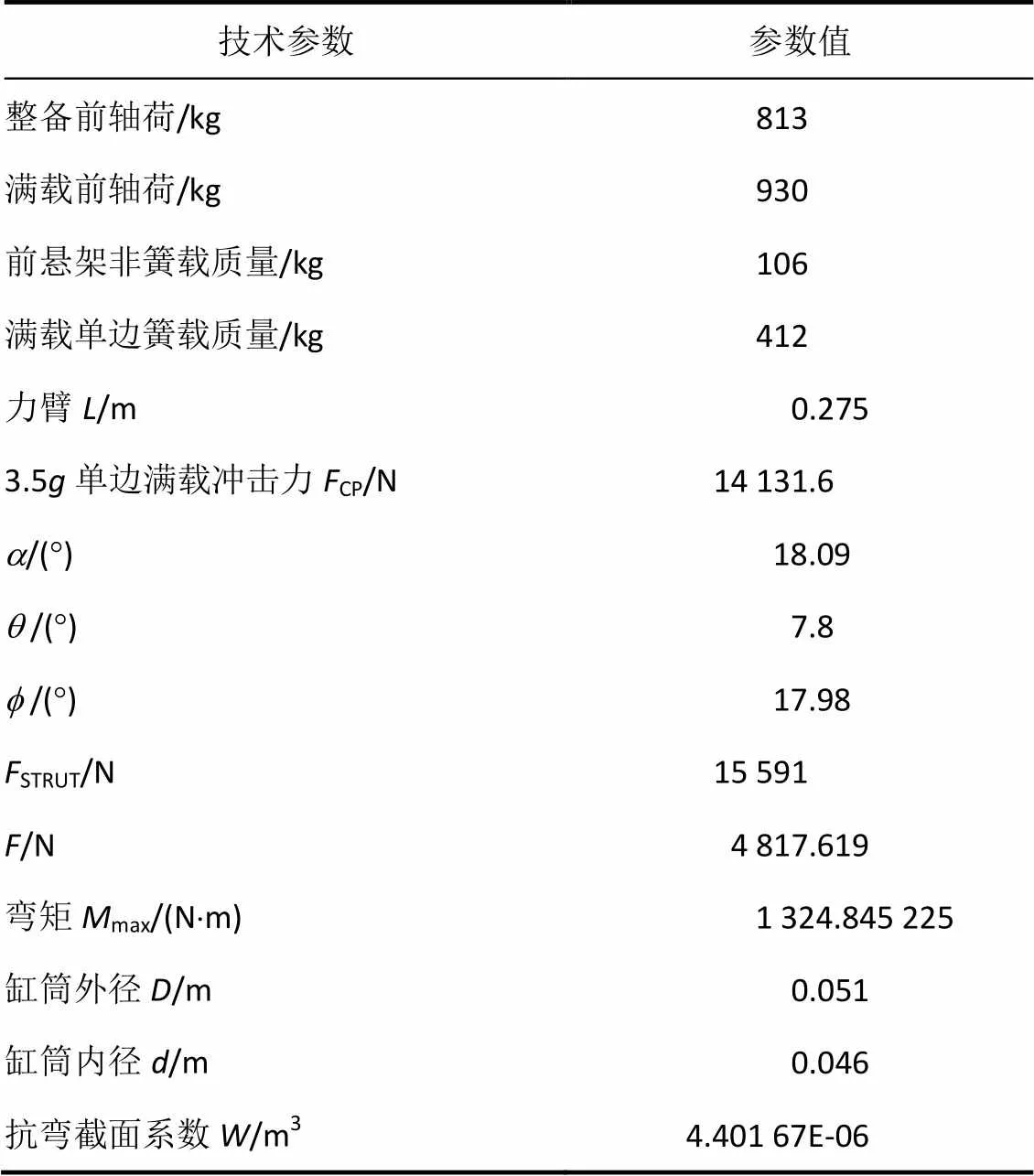
表1 故障车辆的相关技术参数

表1中参数在车辆开发初期，可以通过平面分析法进行投影和直接测量，较为容易获得。

将参数值代入式（3）～（6），可得该减振器外缸筒承受的最大弯曲应力max=300.98 MPa。

所选减振器外缸筒材料应满足最大弯曲应力大于300.98 MPa。经查，该减振器外缸筒材料为ST37-2，该材料屈服强度为235 MPa，小于300.98 MPa；因此在路试过程中出现了弯曲漏油失效现象，平面分析法的校核结果与试验结果相符。

3 改进与验证

解决失效问题有两种途径：（1）增加外缸筒壁厚，但该方案会导致诸如设备工装等其他组件随之更改，更改量太大，整改周期过长，不予采用；（2）重新选择屈服强度更高的材料，该方案更改量最小，常见的无缝钢管材料有S500MC，该材料屈服强度达到500 MPa，远大于设计计算的理论值300.98 MPa，采用该材料后，经多次路试均未出现减振器漏油失效现象，对减振器外缸筒进行测量，如图5所示，没有发现弯曲变形情况，也没有出现减振器漏油失效现象，满足设计要求。

图5 减振器外缸筒正常无弯曲

4 结 论

1）在减振器设计初期，采用平面分析法可以较快捷地获得减振器受力的弯矩强度，经验证可获得较为可靠的参考数据。

2）减振器外缸筒作为簧下质量不能设计得过于厚重，但其抗弯扭能力应进行充分校核，确保其具备足够的抗弯扭能力。

[1]刘鸿文. 材料力学Ⅰ[M]. 5版. 北京：高等教育出版社，2011.

2018-12-19

1002-4581（2019）02-0034-04

U463.33+5.1

A

10.14175/j.issn.1002-4581.2019.02.009