经历循环荷载历史后饱和混凝土动态性能试验研究
李少丽 刘立荣 王乾峰
(石家庄铁路职业技术学院1) 河北石家庄 050041 三峡大学土木与建筑学院2) 湖北宜昌 443002)
近年来,随着水利工程的大规模建设,混凝土在水环境中的应用越来越广泛,学者们对混凝土材料的研究也逐步拓展到了水环境混凝土,并取得了一些研究成果。Rossi[1]、李庆斌[2~3]、杜守来[4]、刘博文[5]等国内外学者研究了混凝土材料在水环境中的抗压强度、弹性模量等物理力学参数;王海龙[6~7]从细观层次分析了湿态与饱和混凝土的损伤破坏机制;Yaman[8]、郑丹[9]、白卫峰[10]、王乾峰[11]研究了孔隙和孔隙水对混凝土强度和弹性模量的影响;李宗利[12]通过试验研究了高渗透孔隙水压对混凝土力学性能的影响;黄常玲[13]、杜守来[14]研究了孔隙水压条件下混凝土的损伤及破坏机理;彭刚[15]、田为[16]对有压孔隙水环境中的混凝土动态抗压性能、率效应特性进行了试验研究;Chen[17]对干燥和饱和混凝土在不密封和密封两种条件下的抗压强度进行了对比分析;姬永生[18~19]研究了混凝土孔隙水饱和度的影响因素,建立了混凝土内孔隙水饱和度的计算模型;黄仕超[20]、邓媛[21]通过试验研究了循环孔隙水压对混凝土力学性能的影响及损伤特性。
现有研究成果表明混凝土的动静态力学性能受水环境的影响较大,但是目前对饱和混凝土动态特性受循环荷载历史次数的影响研究鲜有报道,而循环荷载历史在一定程度上又能模拟地震动力响应,对其进行研究可以为混凝土结构抗震设计、评估等提供一定的理论基础和试验依据。基于此,本文对经历循环荷载历史后的饱和混凝土动态力学性能进行了试验研究。试验通过对饱和混凝土试件在经历不同荷载循环次数(0次、25次、50次、100次)及不同应变速率(10-5/s、10-4/s 、10-3/s 、10-2/s)作用下的力学性能进行单轴压缩试验,对峰值应力、峰值应变、弹性模量等物理力学参数的变化规律进行了统计分析,研究了荷载循环次数和应变速率对经历循环荷载历史后混凝土力学性能的影响。
1 试验过程
1.1 试件制备
本试验采用φ150×300mm的圆柱体混凝土试件,试验用水泥为湖北宜昌三峡水泥有限公司生产的P.O 42. 5 硅酸盐水泥;粗骨料为粒径5~30mm的连续级配碎石;细骨料为河砂,细度模数为1.8;拌合水为自来水;混凝土的配合比见表1。

表1 混凝土每立方米材料用量 kg/m3
试件用钢模浇筑成型,搅拌方式为先干拌后湿拌的机械搅拌方式。试件成型后先在室温环境下静置24 h然后拆模并编号,接着在标准养护室(温度20℃±2℃,相对湿度95%以上)养护28天,取出后放置于干燥房间内。试验前对试件的两个端面进行磨平处理以避免在试验过程中出现试件偏心受压及应力集中现象。
1.2 试验设备
试验设备为三峡大学大型多功能液压伺服静动力三轴仪,该设备的主要组成部分包括控制系统、伺服系统控制器、加载框架系统、液压油泵、围压系统和计算机系统等。该设备加载框架系统可用于对试件进行3个方向加载,其水平向和竖向的最大动静力加载负荷分别为5 000 kN和10 000 kN;围压系统可施加最大围压为30 MPa,用来对试件进行饱和处理。
1.3 试验步骤
本试验是研究饱和状态混凝土在经历循环荷载历史后的力学性能,因此在力学试验前先对混凝土试件进行水饱和处理。混凝土试件饱和处理利用试验设备围压系统的围压桶。
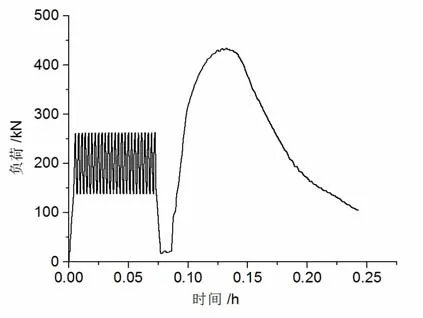
图1 循环荷载的时程曲线
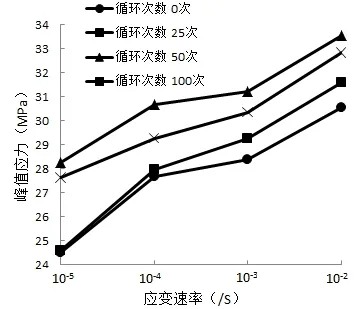
图2 混凝土峰值应力随应变速率的关系
将混凝土试件放入围压桶,并在围压桶内充满水,之后施加1MPa的水压力,直至水位移保持稳定。根据梁辉[22]的试验结果,本试验的保水过程持续 21小时以上,此时数据采集软件界面显示的保水曲线的水位移保持不变,认为混凝土试件达到饱和状态。此后,卸载水压力,取出混凝土试件,再进行后续的力学加载试验。
力学加载过程分为四个阶段:第一阶段以200 N/s的速度对混凝土试件施加200 kN的预加静态荷载;第二阶段按余弦波对混凝土试件进行循环等幅加载,循环次数分别为0、25、50和100次,幅值60 kN,频率0.1 Hz;第三阶段以200 N/s的速度卸载至10 kN;第四阶段对卸载后的饱和混凝土试件,再按设定的应变速率(10-5/s、10-4/s、10-3/s和10-2/s)进行加载,直至试件完全破坏。在试验过程中,前三个阶段采用荷载控制,第四阶段采用变形控制。循环荷载的时程曲线如图1所示。
2 循环荷载历史后饱和混凝土的力学性能
2.1 饱和混凝土峰值应力分析
经历不同循环加载历史次数后的饱和混凝土在 10-5/s、10-4/s、10-3/s、10-2/s四种应变速率作用下的峰值应力,如表2所示。
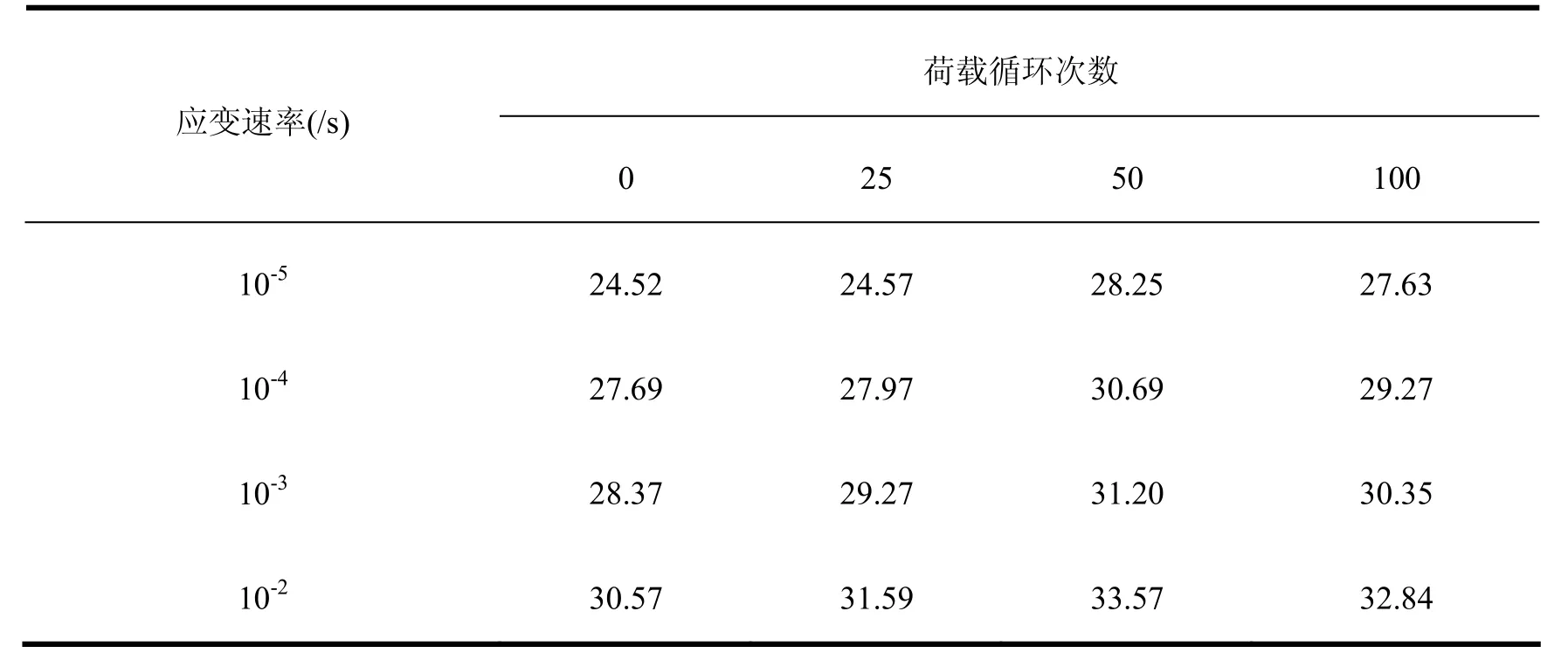
表2 循环荷载历史后饱和混凝土的峰值应力 MPa
经历不同荷载循环次数后,饱和混凝土的峰值应力随应变速率的变化关系见图2。从图2可以看出,当荷载循环次数相同时,随着应变速率的提高,饱和混凝土的峰值应力明显增大。未经历循环荷载时相较于准静态应变速率10-5/s,在10-4/s、10-3/s、10-2/s应变速率下的峰值应力分别提高了12.93%、15.70%、24.71%;经历 25次循环荷载历史时峰值应力分别提高 13.82%、19.12%、28.57%;经历 50次循环荷载历史时峰值应力分别提高了8.62%、10.42%、18.84%;经历100次循环荷载历史时峰值应力分别提高了5.94%、9.84%、18.85%。
不同应变速率下饱和混凝土峰值应力与荷载循环次数的关系见图3。从图3可以看出,在应变速率相同的情况下,随荷载循环次数的增加,饱和混凝土的峰值应力表现出先增大后减小的规律,当荷载循环次数达到50次时饱和混凝土的峰值应力达到峰值,随后随着荷载循环次数的继续增加饱和混凝土的峰值应力逐步降低。
循环荷载次数对饱和混凝土峰值应力的影响分为两个阶段。在低次数的循环荷载历史情况下,饱和混凝土的内部缺陷与初始微裂纹在机械循环的挤压作用下变得更加密实,从而导致饱和混凝土的峰值应力在一定程度上得到提高,在单调加载过程中峰值应力会随着荷载循环次数的增加而增大;但在高次数的循环荷载历史情况下,饱和混凝土的内部缺陷和微裂缝在经过机械循环压实后,随着荷载循环次数的继续增加,混凝土内部在旧裂缝持续发展的同时继续产生新的裂缝,新裂缝的产生导致在单调加载过程中饱和混凝土的峰值应力下降。
2.2 饱和混凝土峰值应变分析
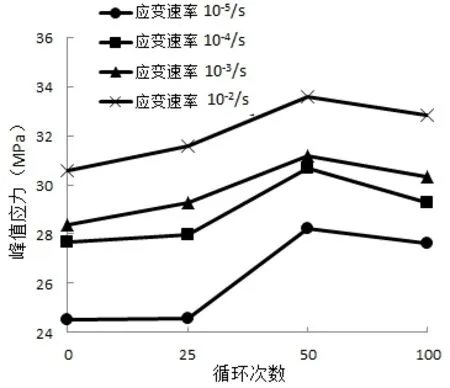
图3 饱和混凝土峰值应力与荷载循环次数的关系
饱和混凝土在不同荷载循环次数与不同应变速率下的峰值应变见表3。

表3 循环荷载历史后饱和混凝土的峰值应变 ×10-3

图4 饱和混凝土峰值应变随应变速率的关系

图5 饱和混凝土峰值应变与荷载循环次数关系
经历不同荷载循环次数后的饱和混凝土的峰值应变随应变速率的变化关系见图4。从图4可以看出,混凝土的峰值应变随应变速率的增加总体呈增大的趋势。对于经历0次、25次、50次和100次循环荷载历史后的饱和混凝土,增大趋势不明显,各应变速率与准静态加载速率10-5/s相比,应变速率10-2/s时峰值应变变化幅度分别为26.36%、2.08%、8.66%和11.74%。这主要是因为在较高的应变速率下,饱和混凝土中的微裂缝是沿着最短路径发展的,并且裂缝数量也较少,从而导致应变速率越高,饱和混凝土的最终变形越大。
不同应变速率下饱和混凝土峰值应力与荷载循环次数的关系见图5。从图5可以看出,随着荷载循环次数的增加,饱和混凝土的峰值应变总体表现为先增大后减小的变化规律。对于饱和混凝土,在应变速率为10-5/s、10-4/s和10-3/s时,历经25次、50次和100次循环荷载历史后的峰值应变与未受加载历史的混凝土相比,峰值应变变化最大幅度分别为20.92%、6.28%和17.57%。可以看出荷载循环次数对饱和混凝土峰值应变有一定的影响,荷载循环次数越低饱和混凝土的延性越好。
2.3 饱和混凝土弹性模量分析
本文以混凝土强度35%~45%时应力应变曲线的割线模量作为饱和混凝土的弹性模量代表值,在不同荷载循环次数、不同应变速率下的弹性模量如表4所示。

表4 循环荷载历史后饱和混凝土的弹性模量GPa
经历不同荷载循环次数后混凝土弹性模量随应变速率的变化关系如图6所示。从图6可以看出,混凝土的弹性模量随应变速率呈现出增大的趋势。经历0次、25次、50次和100次循环荷载历史后,饱和混凝土的弹性模量比静态应变速率下的弹性模量增大了41.66%、21.29%、23.92 %和16.88%。分析认为经历循环荷载历史后的饱和混凝土内部存在细观裂缝,当应变速率为10-2/s时,裂缝直接穿过混凝土粗细骨料以最短路径快速发展,饱和混凝土的形变比低应变速率下的小,从而导致其弹性模量比低应变速率下弹性模量偏高。
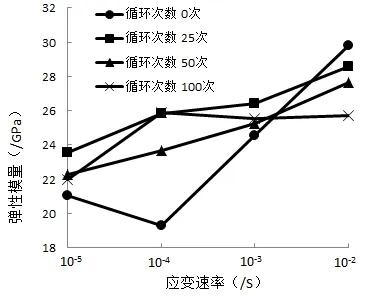
图6 混凝土弹性模量随应变速率的关系
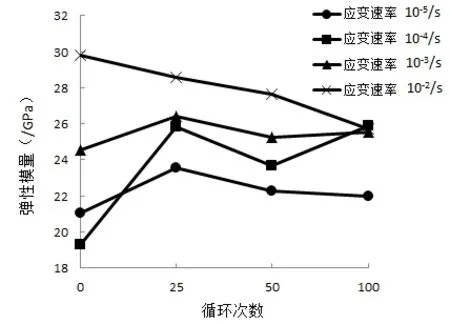
图7 混凝土弹性模量与荷载循环次数的关
不同应变速率下饱和混凝土的弹性模量随荷载循环次数的变化关系如图7所示。从图7可以看出,在应变速率为10-5/s~10-3/s下,随荷载循环次数的增大,饱和混凝土的弹性模量整体表现出先增大后减小的变化规律,当荷载循环次数为25次时弹性模量达到最大值,然后随着荷载循环次数的不断增加,混凝土的弹性模量下降。当应变速率为10-2/s时,饱和混凝土的弹性模量与荷载循环次数成反比,即弹性模量随着荷载循环次数的增加不断降低。
3 结论
(1)经历循环荷载历史后的饱和混凝土随着应变速率的增大其峰值应力也增大,随荷载循环次数的增加其峰值应力出现先增大后减小的规律,经历50次荷载循环次数后的混凝土峰值应力达到最大。
(2)随着荷载循环次数的增加,饱和混凝土的峰值应变先增大后减小;随应变速率的增大,饱和混凝土的峰值应变总体呈增大的趋势,荷载循环次数对饱和混凝土的峰值应变有一定影响,荷载循环次数越小,饱和混凝土的延性越好。
(3)随着应变速率的增加,饱和混凝土的弹性模量表现出逐渐增大的趋势。当应变速率为10-2/s时,饱和混凝土的弹性模量与荷载循环次数成反比。而应变速率为10-5/s~10-3/s时,随着荷载循环次数的增大,饱和混凝土的弹性模量整体表现出先增大后减小的变化规律。

