跑步运动压缩裤压力预测模型的建立*
夏 明,2,3 宋 婧,2,3 张 平 姜朝阳
1. 东华大学服装与艺术设计学院,上海 200051;2. 同济大学上海国际设计创新研究院,上海 200092;3. 东华大学现代服装设计与技术教育部重点实验室,上海 200051
跑步运动会带来一定的肌肉损伤和疲劳。紧身运动装备利用材料的弹性对人体躯干部位进行束缚,达到保护肌肉并避免损伤的作用[1]。可是人体能承受的服装压力有一定限度,过大会使人体疲劳加剧,引起呼吸加快或血液循环障碍等生理不适[2],过小则无法减缓肌肉酸痛或恢复体力。JAKEMAN等[3]通过增强式跳深训练试验得出,穿着压力长袜的受试者相比没有穿着压力长袜的受试者,前者肌肉酸痛感有显著改善。因此,对紧身运动装备的服装压力进行更精确的研究具有重要意义,其对跑步运动压缩裤的量身定制有指导作用。
李红等[4]介绍了循序递减压力袜的作用原理及应用、生产工艺、压力性能及测试方法等。倪海燕[5]基于下肢受压迫时皮肤血流的变化,探讨了压迫对人体生理的影响,为紧身类服装的开发和研究提供了科学依据。YY/T 0853—2011《医用静脉曲张压缩袜》提出,保健压力袜的压力值一般在1.06~2.66 kPa即8.0~20.0 mmHg,压力沿着腿部由下向上递减。李新阳[6]采用非均匀有理B样条函数建立了平针织物的线圈样条函数模型,并较准确地描述了压力袜在线圈形态和长度发生变化时织物压力分布的变化情况。欧亚[7]基于静脉曲张袜的袜筒横向尺寸和压力值的分析,得到了送纱速度与横向尺寸的函数关系,这对静脉曲张袜的生产有指导作用。HONG等[8]利用智能人台检测穿着服装时的压力发现,各测试点的压力明显不同。此外,还有学者对面料在一定拉伸率条件下产生的服装压与拉伸力进行了相关性检验,发现二者之间存在显著的正相关关系[9]。候昀彤等[10]研究了女性大腿股动脉止血点处横截面的形态,发现曲率越大的部位对应的压力值越大,这为医用止血产品的研究提供了参考。
本文以人体工程学为基础,通过对面料拉伸率和曲率的研究,建立腿部服装压力预测模型即圆筒状压力预测模型(简称“圆筒模型”),并验证了线性回归方程的拟合程度,再通过三维人体扫描试验,研究人体腿部穿着跑步运动压缩裤前后的尺寸和截面形态的变化,分析影响圆筒模型压力预测的因素。
1 圆筒模型的建立
1.1 面料的选择与性能测试
1.1.1 面料的准备与测试方法
选取市面上跑步运动压缩裤使用较为普遍的针织面料用于压力预测模型的建立。该针织面料由质量分数占80%的锦纶和质量分数占20%的氨纶组成。利用INSTRON万能电子强力仪测定该针织面料的拉伸性能。根据FZ/T 70006—2004《针织物拉伸弹性回复率试验方法》,从距离布端1.5 m以上处裁剪出被测面料,接着采用等速拉伸法,测试面料的拉伸性能,仪器自动记录面料拉伸至断裂时的载荷-位移曲线。
1.1.2 面料的测试结果与分析
基于该面料的载荷-位移曲线关系得出,该面料的横向断裂拉伸率可达到300%左右,适用于跑步运动压缩裤的制作。接着对面料拉伸率在60%以内的拉伸力与拉伸率进行直线拟合(图1)和回归分析,发现:当拉伸率不超过60%时,面料的变形为弹性变形,面料在该拉伸率范围内产生的服装压力具有参考性。

图1 拉伸力与拉伸率的直线拟合及回归分析(拉伸率≤60%)
1.2 圆筒模型的建立
1.2.1 试验准备与测试方法
选择AMI3037号气囊式压力测试仪测量服装压力,研究圆筒模型曲率(半径的倒数)和面料拉伸率对服装压力的影响。
跑步运动压缩裤的样版设计主要针对脚踝周长、小腿最大围、膝围、大腿最大围等尺寸。本文对200名在校研究生的人体部位尺寸进行了人工测量,得到在校研究生脚踝周长、小腿最大围、膝围和大腿最大围的平均值分别为20.5、 34.2、 35.5和52.0 cm。因此,本文选择4个不同周长(即20.5、 27.0、 35.5和48.0 cm)的光滑刚性圆筒模型用于压力预测,高度均为20.0 cm,分别记作1#、 2#、 3#、 4#,其曲率依次减小。
试验设置了7个面料拉伸率值,分别为0%、 10%、 20%、 30%、 40%、 50%、 60%。利用式(1)可计算出4个不同周长圆筒模型预测压力用的28块面料纬向的原始长度:

(1)
式中:ε——拉伸率,%;
L0——面料纬向的原始长度,cm;
L1——面料纬向的拉伸后长度,cm。
压力值测试步骤:
(1) 根据计算得到的面料纬向的原始长度,两端再加放0.5 cm的缝份,使用绷缝机将面料缝制成高度均为15.0 cm圆筒试样。
(2) 在距离圆筒模型底部7.5、 15.0 cm处各画1条水平线。在距离圆筒试样底部7.5 cm处画1条水平线,再均匀地画3条垂直线。
(3) 校准仪器,将2个气囊分别黏贴在距离圆筒模型底部7.5 cm水平线上的对称部位(图2),记录静止时气囊的压力值。
(4) 为减少面料自身厚度对压力值的影响,压力测试时特将缝份放在外表面,测试并记录压力值。
每块圆筒试样及对应的圆筒模型测试时,都需重复以上步骤。

图2 气囊使用示意
1.2.2 试验结果及分析
表1所示为28块圆筒试样测得的压力值。

表1 28块圆筒试样测得的压力值
由表1可知:当曲率相同时,拉伸率越大,圆筒模型所受的压力越大;当拉伸率相同时,曲率越大,圆筒模型所受压力越大;对于不同的曲率,拉伸率越小,圆筒模型所受压力越接近。基于此可以判定,压力与曲率、拉伸率之间存在一定的相关性。
接着,利用SPSS软件对Pearson简单相关系数、Spearman等级相关系数和Kendall相关系数进行多元线性回归分析。同时,为了消除解释变量(即可控制变量或说明变量)的个数对相关系数的影响,利用调整的判定系数即R2检验线性回归方程的拟合优度,发现调整后的R2=0.912,说明拟合效果较好。线性回归方程为F=-0.70+4.34k+4.74ε,其中:F为服装压力,kPa;k为曲率,cm-1;ε为拉伸率。此外,从表2的线性回归计算结果中可以看出,T检验的显著性水平均小于0.050,这表明线性回归方程显著。

表2 线性回归计算结果
2 跑步运动压缩裤穿着压力测试
2.1 跑步运动压缩裤的制作
使用Creaform HandySCAN 3D三维扫描仪,以身体质量指数(BMI)为标准,对3名受试者(分别为偏瘦体1号、正常体2号和肥胖体3号)进行三维人体数据采集,再根据三维人体点云计算出主要部位的围度和高度(表3)。
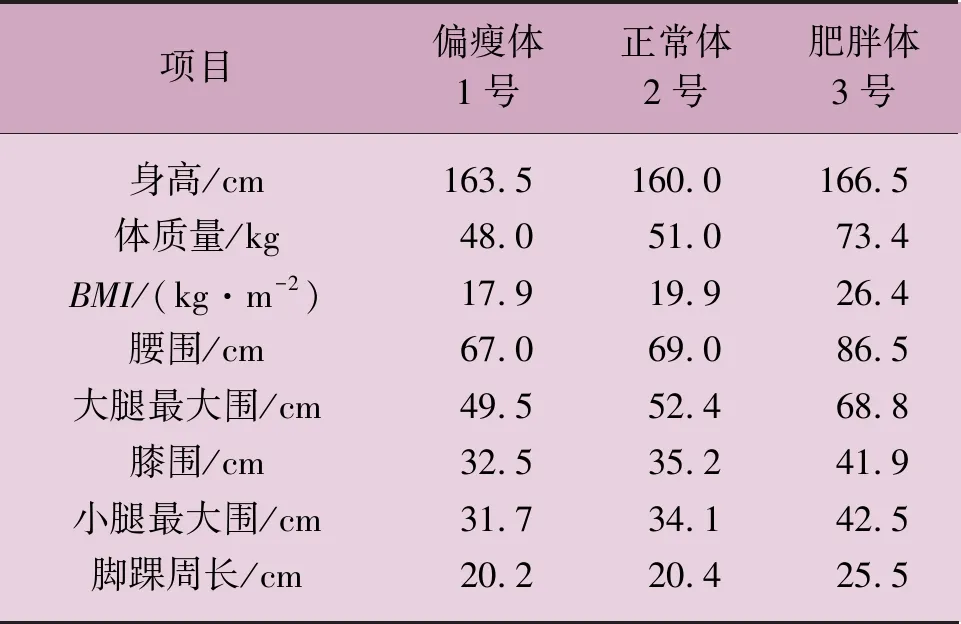
表3 3名受试者数据采集
跑步运动压缩裤压力值的设计参考知名压缩裤品牌SKINS设计的梯度压力值,脚踝处的压力值在(2.57±0.47)kPa即(19.3±3.5)mmHg,脚踝处到腰部的压力值依次逐级递减。因此,本文将3位受试者脚踝处的压力值设计为2.54 kPa即19.1 mmHg。3位受试者腿部主要部位的拉伸率设计如表4所示。在不考虑其他因素影响的前提下,根据拉伸率计算式及人体对应部位的尺寸,计算出跑步运动压缩裤的尺寸,从而得到3种体型的跑步运动压缩裤样板。最后利用绷缝机进行压缩裤的缝制。

表4 跑步运动压缩裤主要部位拉伸率的设计 (%)
2.2 压力测试
2.2.1 测试过程
(1) 根据跑步运动压缩裤样版各部位的高度尺寸,在跑步运动压缩裤对应部位做好标记,再用马丁测量仪在人体对应部位(如脚踝处、小腿最大围处等)做好标记,并在这些围度上均匀地标记8个测量点。
(2) 对气囊式压力测试仪进行校准。考虑到气囊本身厚度的影响,对各部位水平围度一周的8个点分2次进行测量,记录静止时气囊的压力值。
(3) 检查穿着好跑步运动压缩裤时,各部位的水平线是否与地面保持水平。
(4) 测试并记录压力值。
每条跑步运动压缩裤和对应受试者进行测量时,都需重复以上步骤。
2.2.2 测试结果与分析
对每个部位8个点的压力值计算平均值即为实测值,其与对应的压力预测值一起归纳于表5中。
表5 3位受试者压力预测值和实测值

(kPa)
从表5可以看出:小腿最大围处、膝盖处和大腿最大围处压力的预测值虽比实测值大,但整体上较接近,且压力值都是从小腿最大围处往大腿最大围处逐渐递减的,因此线性回归方程可用于预测小腿最大围处、膝盖处和大腿最大围处的压力值;脚踝处压力的实测值与预测值差异较大,原因与脚踝处压力影响因素较多有关。
3 圆筒模型压力预测影响因素分析
3.1 腿部围度尺寸数据分析
3.1.1 不同人体腿部围度
偏瘦体1号和肥胖体3号穿着跑步运动压缩裤前后围度的尺寸差值如图3所示。在肥胖体3号膝盖处、小腿最大围处、脚踝处所受的压力都小于偏瘦体1号的情况下,肥胖体3号的压缩变形值基本大于偏瘦体1号。两位受试者着装前后,在大腿部(对应的人体腿部截面高度为35.0~60.0 cm)的围度尺寸差明显大于其他部位,即脂肪含量越多,压缩变形越明显。偏瘦体1号和肥胖体3号着装前后在脚踝处的围度尺寸差基本为0.0 cm,即穿着跑步运动压缩裤后脚踝处没有产生压缩变形。

图3 偏瘦体1号和肥胖体3号着装前后腿部围度尺寸差
3.1.2 不同跑步运动压缩裤腿部围度
正常体2号分别穿着高度相同、围度尺寸不同的S、 M、 L码跑步运动压缩裤后进行三维人体扫描,数据提取方法同偏瘦体1号和肥胖体3号。结果发现,穿着S、 M和L码的跑步运动压缩裤前后,正常体2号遵循压力越大其围度尺寸差越大,且脂肪含量越多的部位其围度尺寸差越大的规律。
3.2 腿部围度截面形状分析
在腿部围度尺寸提取的过程中可得到人体腿部的点云数据。以偏瘦体1号为例,将同一高度对应围度上的点整理后进行截面图形绘制,可得到如图4所示的截面。
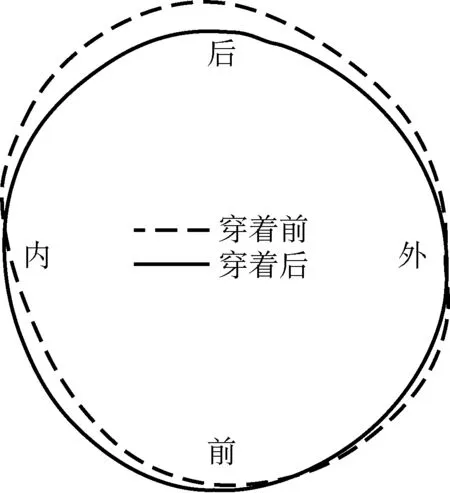
图4 偏瘦体1号大腿最大围处着装前后截面形状对比
穿着跑步运动压缩裤后,腿部形状发生了变化,围度尺寸减小。因人体本身在大腿最大围处和小腿最大围处的截面接近圆形,穿着跑步运动压缩裤后截面更趋向于圆形。因此,利用圆筒模型预测大腿最大围处和小腿最大围处的压力,效果较好。
图5所示为偏瘦体1号穿着跑步运动压缩裤前后膝盖处的截面图,由于膝盖处的结构较复杂,穿着跑步运动压缩裤后线条变圆滑,原因与压缩使部分脂肪产生了形变有关,也可能与后中和前中的曲线在人体上有一定的弧度,压缩裤未能完全贴合人体从而造成穿着后的截面曲线趋于圆滑有关。比较膝盖处的压力预测值和实测值可以看出,圆筒模型的预测效果较好。
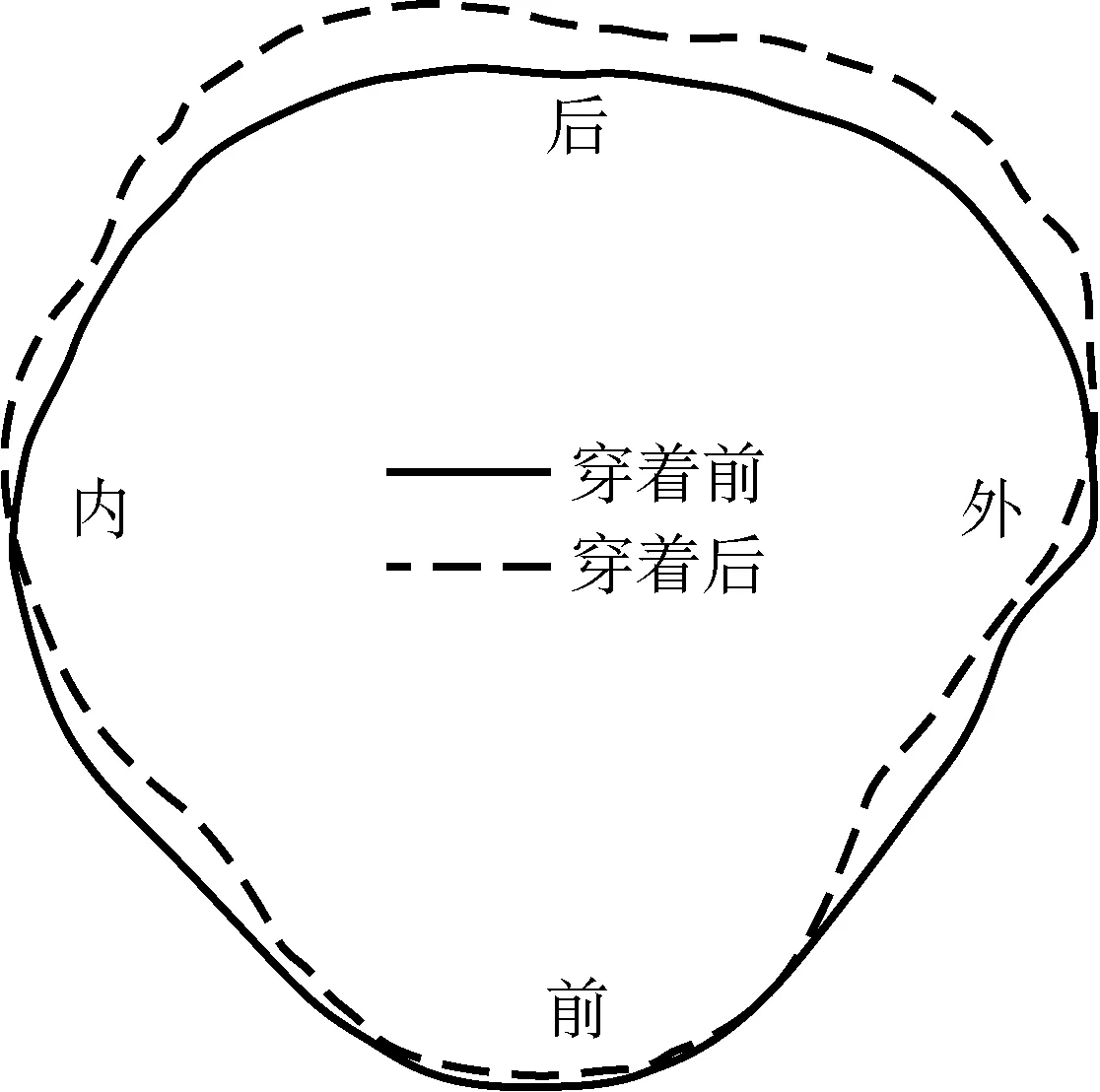
图5 偏瘦体1号膝盖处着装前后截面形状对比
3.3 脚踝处压力预测影响因素
脚踝处的压力值是在距离压缩裤边缘3.0 cm处测得的。现将距离圆筒模型底部7.5 cm的气囊移动至距离圆筒模型底部3.0 cm处,测量压力值。对比发现,在3.0 cm处测得的压力值都小于7.5 cm处测得的压力值,原因可能与测量部位距离裤子边缘较近有关。脚踝处结构较复杂,脂肪少、骨骼多,后中的曲率较大,外侧较平坦,且不同的站姿和不同的用力方式等都会对其压力值造成影响,因此,采用脚踝处8个点的均值来表示该处的压力实测值与预测值差异较大。
4 结论
通过研究服装压力与拉伸率、曲率的关系得到:
(1) 在跑步运动压缩裤压力预测用圆筒模型的建立过程中,当拉伸率控制在0%~60%时,服装压力与拉伸率、曲率都呈正相关关系,并得出了它们三者之间的线性回归方程F=-0.70+4.34k+4.74ε,其中F为服装压力(kPa),k为曲率(cm-1),ε为拉伸率。
(2) 通过测试跑步运动压缩裤的穿着压力,对比实测值与预测值发现,圆筒模型可用于预测除脚踝处的其他腿部压力。
(3) 利用三维人体扫描试验分析不同人体腿部围度尺寸数据、穿着不同跑步运动压缩裤后腿部围度尺寸数据,以及腿部围度截面形状、脚踝处压力预测影响因素得出,脂肪含量相同时,压力值越大则产生的压缩变形越大;压力值相同时,脂肪含量越多的部位产生的变形越大。

