采用六维力传感器检测受力同轴度的方法
谢若龑 张一帆 唐松/上海市计量测试技术研究院
0 引言
轴向加荷材料试验机主要用于材料的力学性能试验。由于加工、安装、使用等多方面因素的影响,材料试验机不可避免地存在受力不同轴问题。受力同轴度误差的存在会在试验过程中引入附加弯矩,从而影响试验结果的准确性。现下,主流的受力同轴度检测方法分为在同轴度试样指定位置粘贴应变片测量应变的应变法和使用两个引伸计测量同轴度试样两侧变形的双引伸计法[1],但两种方法都存在只能检测试样特定方位的变形而遗漏对可能出现最大应变方位的检测,导致无法测得最大受力同轴度的问题。
六维力传感器是一种检测对象在空间所受力与力矩,通过三维正交力和三维正交力矩表达出来的复合型力传感器,能够准确地描述检测点的受力状态。结合六维力传感器可以分析得到同轴度试样横截面的应力分布状态,根据材料特性、应力与应变的关系,可求得同轴度试样任意方位的应变,不遗漏最大受力同轴度。
1 受力同轴度与试样应力的关系
理想情况下进行拉伸试验,材料试验机拉力轴线与试样中心线重合,如图1所示。试样任一横截面的应力为σ=,其中A为试样横截面的面积[2]。

图1 试样理想情况受力示意图
实际情况下,由于受到材料试验机同轴度的影响,试样的实际受力情况如图2左所示[3],其中δ为几何同轴度偏差,α为试验机拉力轴线与试样中心线夹角。其等效受力分析如图2右所示,其中px=pcosα,py=psinα,M=pδ。

图2 试样实际情况受力示意图和等效受力示意图
px产生的正应力,即试样中性层的正应力σ1为

py形成的弯矩对距试样受力面长为L处横截面的最大正应力σ2为

式中:W——抗弯截面系数
M产生的最大正应力σ3为

由应力叠加效应可知,距试样受力面长为L处横截面的最大正应力σmax为

距试样受力面长为L处横截面的最小正应力σmin为

受力同轴度计算公式[4]为

应变与应力的关系为

式中:E——弹性模量
将式(4)(5)分别代入式(7)可得距试样受力面长为L处横截面的最大应变εmax和最小应变εmin为

变形与应变关系为

将式(8)(9)分别代入式(10),可得ΔLmax、ΔLmin为
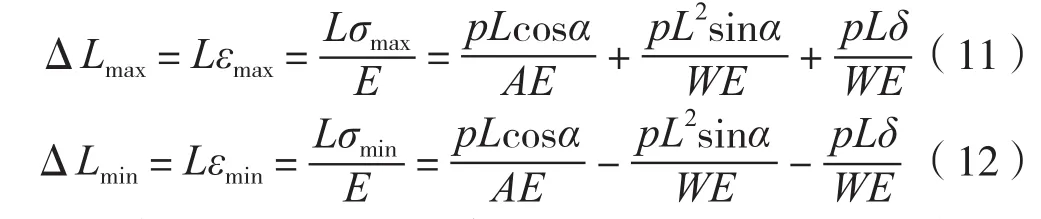
将式(11)(12)代入式(6)可得受力同轴度与应力的关系:

2 受力同轴度仿真
利用有限元分析软件,建立同轴度试样模型,进行同轴度试样的受力仿真,获得同轴度试样应力与变形数据,分析基于式(7)应力计算的受力同轴度与使用双引伸计法测得受力同轴度之间的关系。
这里以250 kN拉力试验机的受力同轴度检测为例,进行同轴度试样的受力仿真,参照JJG 139-2014《拉力、压力和万能表试验机检定规程》[4]中要求,建立如图3所示同轴度试样模型,其中试样均匀段直径d=10 mm,l0=100 mm,L= 130 mm,材质为45#。

图3 同轴度试样示意图
在实际仿真过程中,为便于统计分析,将图2所示的实际情况受力状态分解为拉力轴线与试样中心线夹角为零(α= 0°),以及拉力轴线与试样中心间距为零(δ= 0 mm)两种状态,如图4所示。分别进行仿真,仿真结果如图5所示。双引伸计法中引伸计检测的应变为引伸计标距内的平均应变,根据材料力学可知,同轴度试样在两种受力状态下,试样均匀部分中心(l0=50 mm)处的应变与标距100 mm的平均应变相等。使用有限元分析软件采集关键点数据,分析不同α、δ与试样应力σ、受力同轴度e之间的关系,结果见表1、表2。

图4 α = 0°与δ = 0 mm情况受力示意图

图5 仿真结果示意图
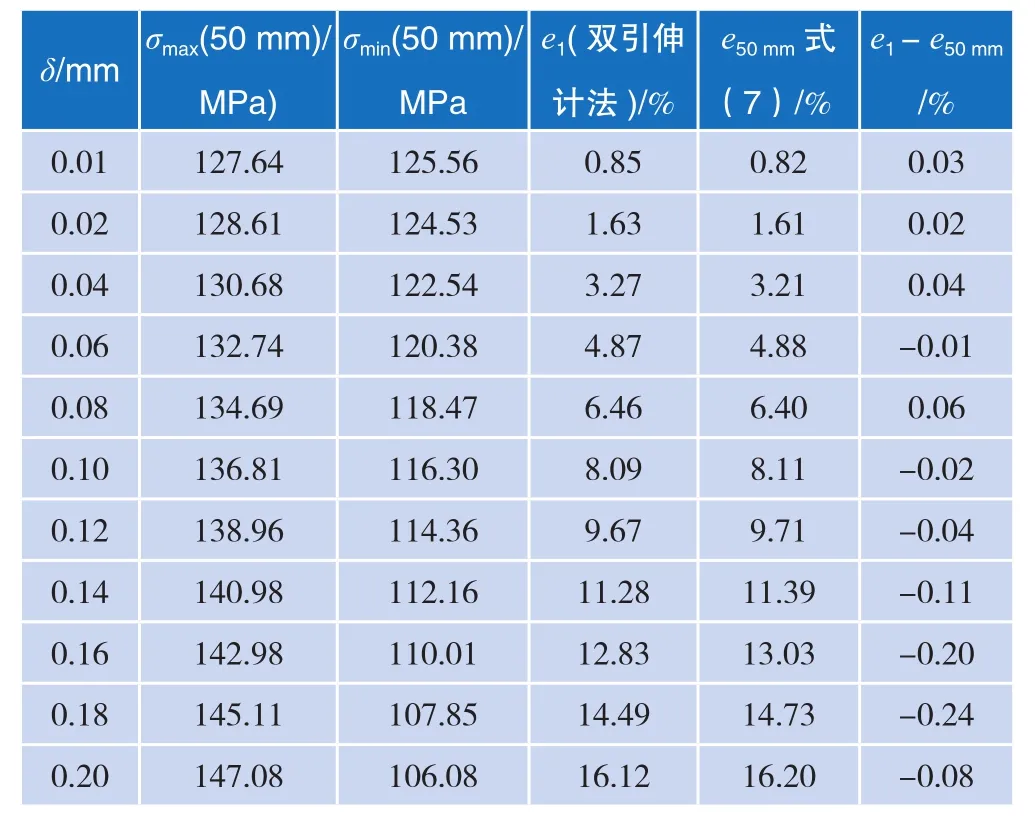
表1 间距δ与受力同轴度e关系表

表2 夹角α与受力同轴度e关系表
由表1、表2可知使用双引伸计法测得与基于式(7)通过应力计算得到的受力同轴度绝对误差的绝对值不超过0.2%,造成这一误差主要原因为有限元网络单元划分引入的关键节点计算结果的不确定性。依照笔者检测经验,材料试验机受力同轴度检测结果重复性一般在2%左右,误差结果可以接受。
3 六维力传感器原理
六维力传感器是一种能同时测量空间给定坐标系三个坐标方向上的力与绕三个坐标轴的力矩这六个分量的传感器,其本质可以认为是一种由特定结构分布的力传感器组,通过对多个力传感器的信号进行处理,以获得被测对象所受的力与力矩。
下面以常见的Stewart结构六维力传感器[5]为例:
Stewart结构六维力传感器是由六个弹性杆件联接上下不同直径的平台而成,通过检测弹性杆件的变形实现六维力的测量,六个弹性杆件可等效为六个力传感器,即Stewart结构六维力传感器是由六个力传感器构成的力传感器组,其结构示意图如图6所示。通过一组标定系数,就可以确定给定坐标系原点(简称:传感器检测点)在三个坐标方向上的力与绕三个坐标轴的力矩,通常情况传感器检测点设在上平台中心,即图6中的B点。
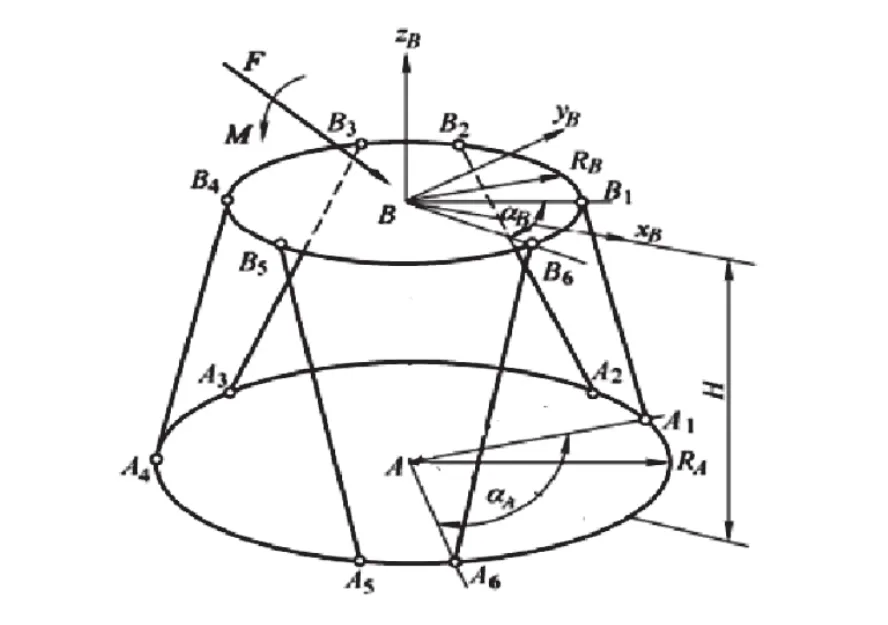
图6 Stewart结构六维力传感器结构示意图
4 基于六维力传感器的受力同轴度检测方法
为六维力传感器添加工装作为同轴度试样,上工装均匀段直径为10 mm,长度为50 mm,夹持部分下端至传感器检测点距离为65 mm,如图7所示,安装于材料试验机。材料试验机加载到相关规程要求的力值,测得传感器检测点在三个坐标方向上的力与绕三个坐标轴的力矩。将获得的数据导入有限元分析软件,得到传感器检测点所在试样横截面的应力分布情况,并依照式(7)计算得到材料试验机的受力同轴度,重复测量三次,取最大值作为被检材料试验机的受力同轴度。

图7 六维力传感器同轴度试样示意图
5 结语
基于六维力传感器的受力同轴度检测方法是应变法的一种衍生,可以解决应变法中粘贴应变片的同轴度试样溯源困难、维护繁琐、失效条件不明确,以及应变法和双引伸计法都存在遗漏最大受力同轴度的问题,但大量程的六维力传感器体积庞大、质量沉重,影响其携带的便携性,加之,现有常见六维力传感器规格的限制,六维力传感器覆盖全规格材料试验机受力同轴度的检测还有困难。随着现有技术不断成熟、新兴技术不断发展、结构设计不断优化,六维力传感器向着小型化、轻量化、大量程化发展。可以预见到,在不久的将来,可以满足更多需求的六维力传感器投入实际检测中。

