高效低存储开销可验证外包求解大规模线性方程组方案

冯 达 周福才 王 强 吴淇毓

(东北大学软件学院 沈阳 110169)

近些年云计算技术有了长足发展，目前已经有包括亚马逊、谷歌、微软、雅虎等许多著名公司提供了针对商业或个人的云计算服务.在云计算服务器上进行计算需要用户外包数据到服务器，这样会导致一系列安全问题[1-2].第1个安全问题是外包计算的隐私性：好奇的云计算服务器不应该了解关于外包计算的任何信息(包括输入和输出).第2个安全问题是外包计算的可验证性：外包用户应该能够检测出云计算服务器的任何恶意行为.另外，在效率方面，要求用户设备需要完成的计算比求解本身计算更高效；在存储开销方面，要求外包方案尽量降低用户所需存储空间.

大规模线性方程组Ax=b是最基本的代数问题之一[3-4].许多现实问题会导致规模非常大且系数非常密集的线性方程组，甚至会有几百万个未知变量.这时，系数矩阵的存储需求很容易超过用户设备可用存储空间.

由于外包服务器不可信，Golle和Mironov[5]最先提出了Ringers概念来解决验证计算的信任问题. Gennaro等人[6]正式提出了可验证计算的模型和方案.由于全同态加密技术效率过低，之后的一些方案[7-8]提高了可验证计算的效率.Parno等人[9]提出一种多功能可验证计算方案.

Atallah等人[10]提出了矩阵乘法和积分计算的安全外包框架.然而，该方案允许泄露私密信息.Atallah和Li[11]提出了一个安全外包序列比较到两个服务器的高效协议.随后Blanton等人[12]为安全外包序列比较提出了一个更有效的方案.Benjamin和Atallah[13]解决了外包线性代数计算的问题，但需要昂贵的同态加密操作.Atallah和Frikken[14]随后提出基于Shamir秘密共享的改进方案.其他一些方案[15-16]也使用Shamir秘密共享在云上执行同态计算.显然，基于秘密共享的协议需要至少2个非共谋服务器.Wang等人[17]提出了安全外包线性规划计算的有效机制.随后，Wang等人[18]又提出了一种基于迭代方法求解大规模线性方程组的安全外包机制，但需要客户端和云计算服务器进行多轮交互.最近Yu等人[19]提出了基于矩阵变换的非迭代外包算法；Shen等人[20]提出了一种分布式安全外包方案；Zhang等人[21]提出了基于置换的外包算法；Chen等人[22]提出了基于稀疏矩阵的高效外包算法；蔡建兴等人[23]提出了一个基于克罗内克函数和随机置换的可验证外包算法.

本文在完全恶意模型(fully malicious model)下提出了一个新的高效低存储开销可验证外包求解大规模线性方程组方案EVLE-LS(efficient verifiable outsourcing of solving large-scale linear equations with low storage overhead).即本方案只需外包计算到单个云计算服务器，该服务器被认为是懒惰的、好奇的、不诚实的.本方案的优势在于：与Gennaro等人在文献[6]中提出的安全外包计算模型相比，取消了公钥pk；在无需复杂的知识证明技术或者布尔乱码电路的条件下实现了完全可验证.在可验证方面优于文献[12]中的方案；在效率方面优于文献[12，22]中的方案；客户端与服务器只需一轮交互过程；与文献[12，22-23]中的方案相比，利用构造的伪随机稀疏矩阵生成算法大幅度降低所需存储开销到常数级.

1 相关知识

1.1 稀疏矩阵概念及性质

定义1.稀疏矩阵(sparse matrix).元素大部分为零的矩阵称为稀疏矩阵.反之，如果大部分元素都为非零元，称之为稠密矩阵.

设A,B是2个普通(非稀疏)n×n矩阵，计算AB或BA需要进行n3次标量乘法运算，即复杂度为O(n3).而若其中1个为稀疏矩阵，不失一般性，设A为每行最多有μ个非零元的n×n稀疏矩阵(μ≪n)，B为任意n×n矩阵，计算AB或BA至多需进行μn2次标量乘法运算.由于μ≪n，所以此时计算AB的复杂度为O(n2).

1.2 严格对角优势矩阵理论

定义2.严格对角优势矩阵(strictly diagonally dominant matrix).如果n阶矩阵A的每一列主对角元素的绝对值均大于非主对角元素绝对值之和，即：

其中,j=1,2,…,n.

引理1.如果n阶矩阵A=(ai j)为严格对角优势矩阵，那么A是可逆的(非奇异的)[24].

1.3 可验证性

因为需要对可验证性进行讨论，此处选用β-Checkability的概念衡量可验证性.

定义3.β-Checkability[25].称方案是功能F的β-Checkability的实现，如果：1)该方案正确实现了F功能；2)对任意输入，服务器不遵守协议的行为都会被以不低于β的概率检测出来.

1.4 矩阵的编码和解码[22]

客户端外包形如Ax=b的大规模线性方程组，其中A是系数矩阵，b是系数向量.

1) 编码过程

① 选取2个随机的可逆稀疏矩阵M,N，令T=MAN，保证A的隐私性.

② 利用伪随机数生成器(pseudo-random generator, PRG)生成一个随机向量r，计算c=Ar+b,d=Mc.

T和d为编码得到的结果.外包到云计算服务器得到返回结果y使得Ty=d.

2) 解码过程

注意到:

d=Mc=M(Ar+b)=M(Ar+Ax)=
MA(x+r)=MAN·N-1(x+r)=Ty,

客户端只需计算x=Ny-r即可求得方程组的解x.

2 EVLE-LS形式化定义及安全需求

EVLE-LS方案包括2方实体，分别是客户端和服务器，如图1所示:

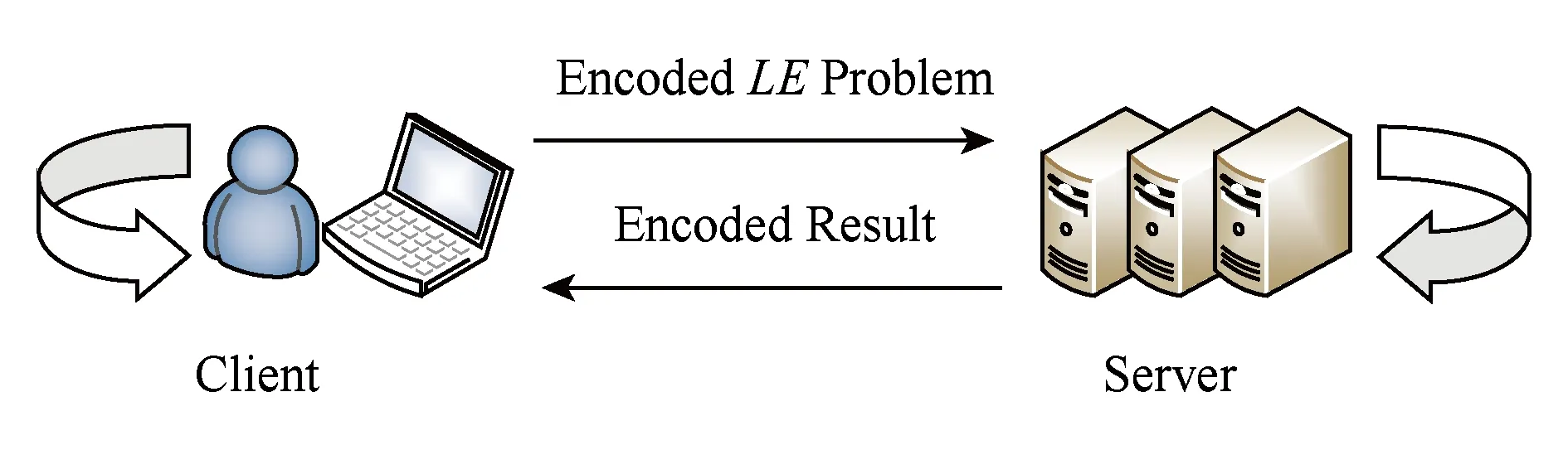
Fig. 1 The architecture of EVLE-LS scheme图1 EVLE-LS方案的体系架构

1) 客户端对线性方程组问题进行编码，将编码后的问题发送给服务器;

2) 服务器进行计算寻找编码后方程组的解，将编码形式的结果返回给客户端;

3) 客户端对返回结果进行验证并根据结果求出原线性方程组的解.

2.1 形式化定义

该外包线性方程组方案包含5个算法：密钥生成算法、问题生成算法、计算算法、验证算法和求解算法，即:

EVLE-LS=(KeyGen,ProbGen,
Compute,Verify,Solve).

每个算法的具体描述如下：

1) 密钥生成算法KeyGen(λ)→(sk).给定一个安全参数λ作为输入，客户端执行该算法生成私钥sk，并由客户端保密.

2) 问题生成算法ProbGen(A,b,sk)→(σA,σb).客户端执行该算法，以系数矩阵A、系数向量b和私钥sk为输入，返回值为A和b的编码形式σA,σb.

3) 计算算法Compute(σA,σb)→σx.客户端发送σA,σb到服务器，服务器以σA,σb为输入计算σx满足σAσx=σb，并返回σx到客户端.

4) 验证算法Verify(σx,sk)→1 or 0.客户端以σx和sk为输入执行该算法，验证σAσx=σb是否成立.若通过验证，则返回1(accept)，否则返回0(reject).

5) 求解算法Solve(σx,sk)→x.如果上一步执行Verify算法通过验证，则输入密钥sk以及σx，客户端运行该算法，输出方程的解x.

2.2 安全需求

安全需求包括正确性，隐私性和不可伪造性.直观上，正确性即结果是正确的；隐私性即服务器无法得知外包计算的任何相关信息；不可伪造性即服务器伪造的结果无法通过验证.下面给出这3种需求的形式化定义.

2.2.1 正确性

首先给出定义输出结果x正确性的实验Experimentcorrectness：

(sk)←KeyGen(λ);
(A,b)←Challenger;
(σA,σb)←ProbGen(A,b,sk);
σx←Compute(σA,σb);
x←Solve(σx).

其中Challenger为挑战者.假设该实验中的算法均被正确执行.

定义4.如果Pr[Ax=b]≥1-negl(λ)，其中negl(λ)是关于安全参数λ的可忽略函数(下同)，则称方案输出结果x是正确的.

2.2.2 隐私性

1) 隐私性一方面指外包方程组的系数的隐私性.即该方案的交互过程中服务器无法得知关于方程组系数的任何信息.下面给出定义EVLE-LS方案中方程组系数隐私性的实验Experimentpri-coef：

(sk)←KeyGen(λ);
((A0,b0),(A1,b1))←A;
(σA0,σb0)←ProbGen(A0,b0,sk);
(σA1,σb1)←ProbGen(A1,b1,sk);
b←{0,1};
b′←A(σAb,σbb).

定义5.如果对所有概率多项式时间(probabilistic polynomial time, PPT)敌手A，满足:

则称方程组的系数具有隐私性.

2) 隐私性另一方面指外包线性方程组的解的隐私性，即服务器无法得知关于方程组解的任何信息.给出定义EVLE-LS方案中解的隐私性的实验Experimentpri-sol：

(sk)←KeyGen(λ);
(A,b)←Challenger;
(σA,σb)←ProbGen(A,b,sk);
σx←Compute(σA,σb);
x0←Solve(σx);
x1←Rn×1;
b←{0,1};
b′←A(σA,σb,σx,xb).

定义敌手A对于方程组解的隐私性的优势为

定义6.如果对所有概率多项式时间敌手A，满足:

则称方程组的解具有隐私性.

2.2.3 不可伪造性

这里的不可伪造性指服务器无法恶意伪造一个结果返回给用户并通过验证.为了更加明确，给出定义不可伪造性的实验Experimentunforgeability：

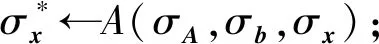
根据上述实验，定义敌手对返回结果不可伪造性的优势为

定义7.如果对所有概率多项式时间敌手A，满足:

则称服务器的返回结果具有不可伪造性.

3 EVLE-LS方案

本方案将存储开销降低到了常数级的核心在于构造了一个伪随机稀疏矩阵的生成算法，客户端只需保存常数个密钥值.理论上可以用任意随机的可逆稀疏矩阵来编码LE问题中的输入，保证输入的隐私性.为了方便实现，选取稀疏的严格对角优势矩阵(sparse strictly diagonally dominant matrix, SSDDM)作为编码矩阵.在3.1节中给出稀疏严格对角优势矩阵的生成算法，并在3.2节中给出了方案的详细描述.

3.1 生成稀疏的严格对角优势矩阵

为生成伪随机的稀疏严格对角优势矩阵，选取3个伪随机数生成器Gpos,Gval,Gdiagval，具体描述为

Gdiagval:I×N→{0,1}B+B′,
(i,nonce)|→10…0‖Gval(i,i,nonce);

其中，Gpos用来生成稀疏严格对角优势矩阵中非零元素的位置；Gval用来生成非零元的数值；Gdiagval用来生成矩阵对角元素的数值，确保对角元素随机性和矩阵的严格对角优势性质.下面给出SSDDM生成算法SSDDMGen的详细描述.

SSDDMGen(k,nonce)→M：

① 初始化零矩阵Mn×n=(mi j)=0.

② 利用Gpos生成第i行非零元所在列的位置ki j.

④ 利用Gdiagval刷新矩阵主对角线上的数值，此处选择简单地将一个B′位的二进制数值串10…0(见注释1)与Gval(i,i,nonce)连结起来，即令mi i=Gdiagval(i,nonce)作为主矩阵对角元素的值.

经上述SSDDMGen过程，由Gpos保证了每行非零元位置的随机性，由Gval保证了非零元数值的随机性(见注释2)，由Gdiagval保证了主对角元素数值的随机性并实现了矩阵的严格对角优势性质.于是算法SSDDMGen实现了生成伪随机稀疏严格对角优势矩阵的功能.

注释1.选择高位补齐的数字时，需满足补齐之后的数值10…0‖valuei i>(2B+1-1)n.上述算法中选择了特定形式的B′位二进制数值串10…0，最差的情况是存在某一行全为{0,1}B中最大的非零元，所以为了满足严格对角优势性质，只需令B′>1+lbn.事实上，当Gpos按列生成行位置时，此处条件将变成B′>1+lbμ.

注释2.如果Gval只有行和列2个输入，就会导致每次生成的矩阵相同位置的值一定相同.为了防止这种情况发生，引入了新鲜值nonce.使用Gval生成valuei ki j时，要求nonce的取值永不重复.

3.2 方案的详细描述

基于3.1节提出的关键算法，本节对EVLE-LS方案中的5个多项式时间算法即密钥生成算法、问题生成算法、计算算法、验证算法和求解算法给出详细描述.

1) 密钥生成算法

KeyGen(λ)→(sk)：客户端运行该算法，给定一个安全参数λ作为输入.算法选择生成3个随机密钥k1,k2,k3∈{0,1}s(λ)，2个新鲜值nonce1,nonce2.然后令sk=(k1,k2,k3,nonce1,nonce2).为了确保之后生成的稀疏矩阵非零元的数值是不可预测的，此处nonce1,nonce2的取值永不重复，且nonce1≠nonce2.

2) 问题生成算法

ProbGen(A,b,sk)→(T,d)：客户端运行该算法，输入LE问题的系数矩阵A和系数向量b，以及算法KeyGen(λ)生成的密钥sk.该算法利用sk对A和b进行编码，详细步骤如下：

① 利用3.1节中构造的SSDDMGen算法生成2个随机的稀疏严格对角优势矩阵.令

M=SSDDMGen(k1,nonce1),
N=SSDDMGen(k2,nonce2).

② 生成随机向量r：

初始化向量r=(r1,r2,…,rn)T=0.选取适当的伪随机数生成器

Gvector:{0,1}s(λ)→{0,1}Bn.

计算Gvector(k3)=t1‖t2‖…‖tn，其中ti∈{0,1}B.再对所有1≤i≤n，令ri=ti.

③ 对输入进行编码，使服务器无法得知关于系数矩阵A和系数向量b的任何信息：

客户端计算：

T=MAN,
c=Ar+b,
d=Mc,

得到了T和d作为问题生成算法的输出.

3) 计算算法

Compute(T,d)→y：客户端将Τ和d发送给服务器，服务器以T和d为输入，计算y的值使得Ty=d，并将结果y返回到客户端.

4) 验证算法

Verify(y)→1 or 0：客户端利用sk恢复矩阵M,N验证Τy=d是否成立.如果成立，Verify输出1，表示该结果可信；反之Verify输出0，表示结果不可信.

5) 求解算法

Solve(y,sk)→x：如果Verify输出1，返回结果y可信，客户端利用sk中的k3恢复向量r，并计算x=Ny-r.求得x即为外包方程组的解.

4 安全性分析

定理1.在完全恶意模型下，EVLE-LS方案得到的结果x是正确的.

证明. 假设方案中所有算法都得到正确执行，则有:

T=MAN,
c=Ar+b,
d=Mc,
x=Ny-r.

于是:

Ty=d⟹MANN-1(x+r)=Mc
⟹A(x+r)=Ar+b
⟹Ax=b.

所以,Pr[Ax=b]=1≥1-negl(λ).

证毕.

定理2.在完全恶意模型下，EVLE-LS方案中外包方程组的系数矩阵A、系数向量b和最终结果x具有隐私性.

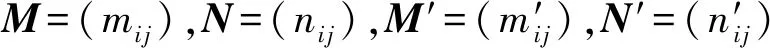
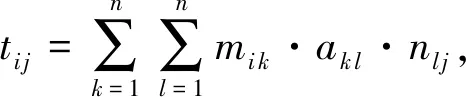
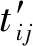
又因为b=M-1d-Ar,x=Ny-r.因为r的随机性可知系数向量b和方程组的解x是具有隐私性的.

综上，

证毕.

定理3.在完全恶意模型下，EVLE-LS方案中服务器的返回结果是不可伪造的.

证毕.

注释3.实际应用中会存在方程组无解的可能，下面考虑外包方程组无解的情况.由于Ax=b无解等价于Ty=d无解，此时服务器只需返回y=∅.该结果正确性显而易见.下面对此种情况的隐私性和不可伪造性进行说明.由定理2的证明过程，系数矩阵A、系数向量b的隐私性与y的存在性无关.唯一会泄露给服务器的信息是：外包的方程组无解，即x不存在.这一点在实际应用中并不会造成隐私泄露问题.又假设存在y*≠∅可以通过验证，则有Τy*=d，与方程Ty=d无解矛盾.

证毕.

综上所述，当Ax=b无解时，本方案仍具有正确性、足够的隐私性和不可伪造性.于是EVLE-LS方案可以在完全恶意模型中处理无解大规模线性方程组问题.

5 性能分析及方案对比

本节首先对EVLE-LS方案各阶段算法的时间复杂度进行分析，再从效率、交互轮次、可验证性、存储开销4个方面将该方案与之前已有方案进行对比，最后对效率进行测试.

5.1 时间复杂度分析

首先从方案中客户端所需的时间复杂度方面对方案的性能进行讨论.

客户端的时间复杂度涉及3个阶段：

1)ProbGen阶段中各步骤的计算以及相应的操作次数为

M,N,r:7G,
T=MAN:2μn2M,
c=Ar+b:n2M+nA,
d=Mc:μnM,

其中,G表示伪随机数生成运算，M代表乘法运算，A代表加法运算.由于G是时间上可忽略的简单映射运算，映射和加法的操作时间与乘法相比是可以忽略不计的.于是可以得出此阶段的时间复杂度为

((2μ+1)n2+μn)M～O(n2).

2)Verify阶段中的计算及相应的操作次数为

M,N:6G,
MANy:((2μ+1)n2)M,

可知此阶段的时间复杂度为

((2μ+1)n2)M～O(n2).

3)Solve阶段中的计算及相应的操作次数为

r:1G,
x=Ny-r:μnM+nA,

可知此阶段的时间复杂度为μnM～O(n).

5.2 方案对比

本节将EVLE-LS方案与文献[12，22-23]中提出的方案进行对比.在效率方面，5.1节中已经给出了对EVLE-LS方案的分析.下面从交互轮次，可验证性和存储开销3方面进行方案对比.

1) 交互轮次.文献[12]中的方案是基于迭代理论的求解方法，但该方案要求客户端和服务器进行L轮交互.而在文献[22]中提出的方案是基于稀疏矩阵编码的外包方案.该方案不需要迭代，也就不需要客户端和服务器进行L轮交互，只需进行1轮交互.EVLE-LS方案也是利用稀疏矩阵对问题进行编码，也具有客户端与服务器只需进行1轮交互的优点.

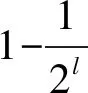
3) 存储开销.与之前已有方案相比，EVLE-LS方案最大的优化在于存储开销方面.文献[12，22-23]中提出的方案需要昂贵的存储开销O(n2)，即客户端需要大量的存储空间.在问题规模足够大时，这种结果是不可接受的.而本方案利用构造的SSDDM生成算法，将存储开销降到了常数级.

下面将以上效率、交互轮次、可验证性、存储开销4个方面讨论结果汇总至表1所示：

Table 1 Capability Comparison with Prior Schemes表1 方案性能比较

Notes: M: An operation of multiplication; G: An operation of PRG; EN: An operation of Paillier encryption; DE: An operation of Paillier decryption;L: The round of iteration;l: A constant.

表1中M表示乘法操作，G表示伪随机函数映射操作，EN和DE分别表示Paillier加密系统中的加密、解密操作.L是所需迭代次数，l是常数.

通过表1可以看出，本方案在效率、交互轮次、可验证性和存储开销4方面均优于文献[12]；在Solve阶段的时间复杂度优于文献[23]；与文献 [12，22-23]相比，以可忽略的操作时间为代价，增加了稀疏严格对角优势矩阵的生成算法.并利用该算法大幅度降低存储开销到常数级.

5.3 效率测试

通过5.2中的理论分析，已经说明了方案的优越性，下面对本方案中服务器端的各阶段算法效率进行测试.实验中，测试工具为MATLAB R2017b，客户端配置为Intel®CoreTMi5-7400 3.0 GHz主频的处理器和8 GB内存.选定L=100，对问题生成算法、验证算法、求解算法3个阶段进行测试.

Fig. 2 Comparison for time consumptions of ProbGen图2 问题生成算法执行时间对比

首先比较4个方案中问题生成算法阶段的效率，实验结果如图2所示，横坐标为矩阵规模的大小，纵坐标为该算法运行的时间.可以看出在该阶段，本方案效率与文献[22-23]中方法基本持平，均为二次曲线，但优于需要Paillier加密操作的文献[12]所述方法.

对比验证算法阶段的效率，实验结果如图3所示.可以看出本方案与文献[22-23]在该阶段效率均为二次曲线，但不受迭代次数L值影响，优于文献[12].

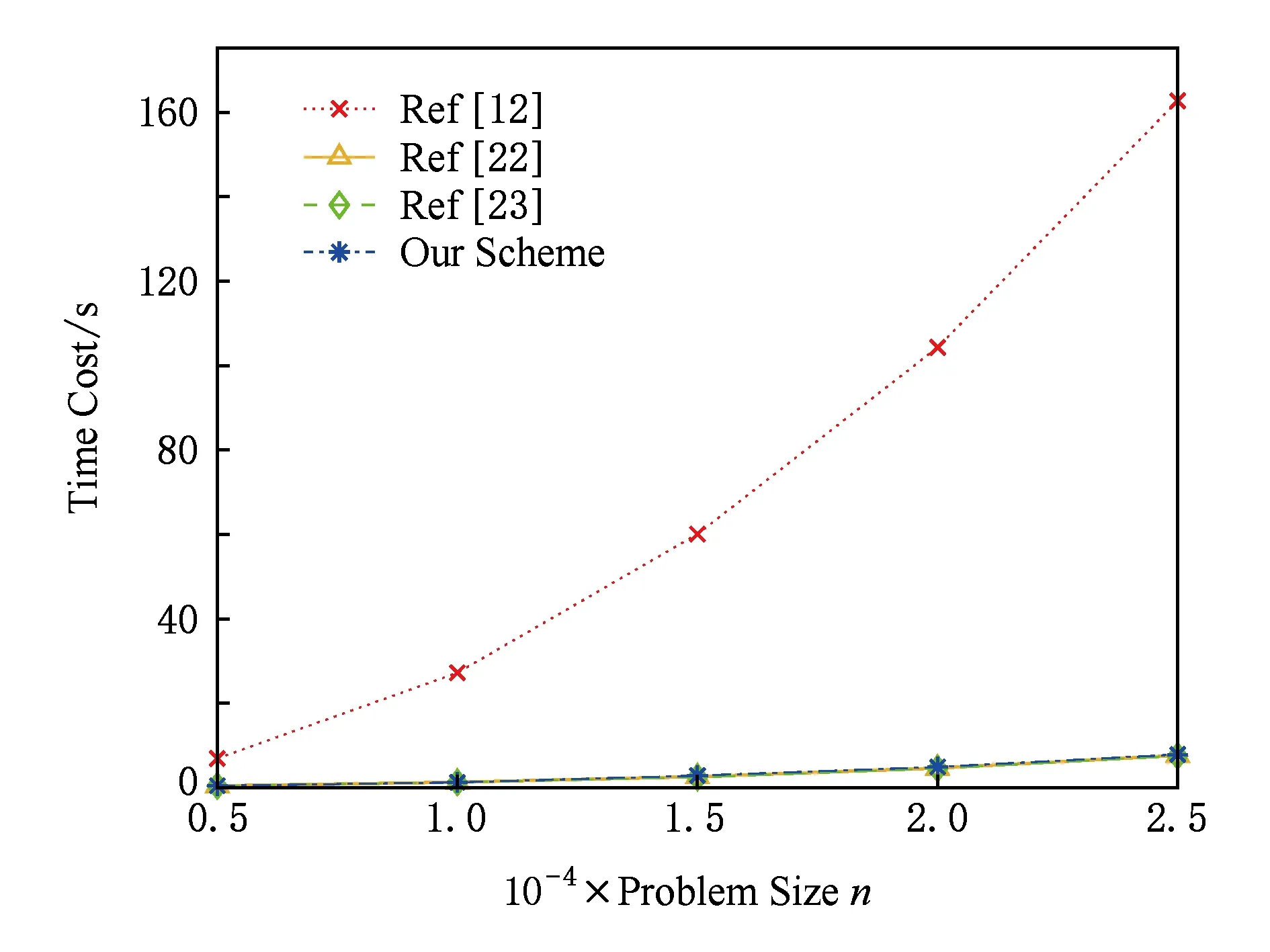
Fig. 3 Comparison for time consumptions of Verify图3 验证算法执行时间对比

对比求解算法阶段的效率，实验结果如图4所示.从图4中容易看出，在求解算法阶段，本方案的时间消耗与问题规模n呈线性关系，算法效率与文献[22]相近，均与问题规模呈线性关系，明显优于文献[23].文献[12]也属线性关系，但涉及Paillier解密操作导致斜率较大.

Fig. 4 Comparison for time consumputions of Solve图4 求解算法执行时间对比

最后比较4个方案中客户端保存密钥的存储开销，实验结果如图5所示，图5中横坐标为问题规模大小，纵坐标为所需存储空间大小.显然，文献[12，22-23]都需要昂贵的存储开销，只有本方案将存储开销降到了常数级.

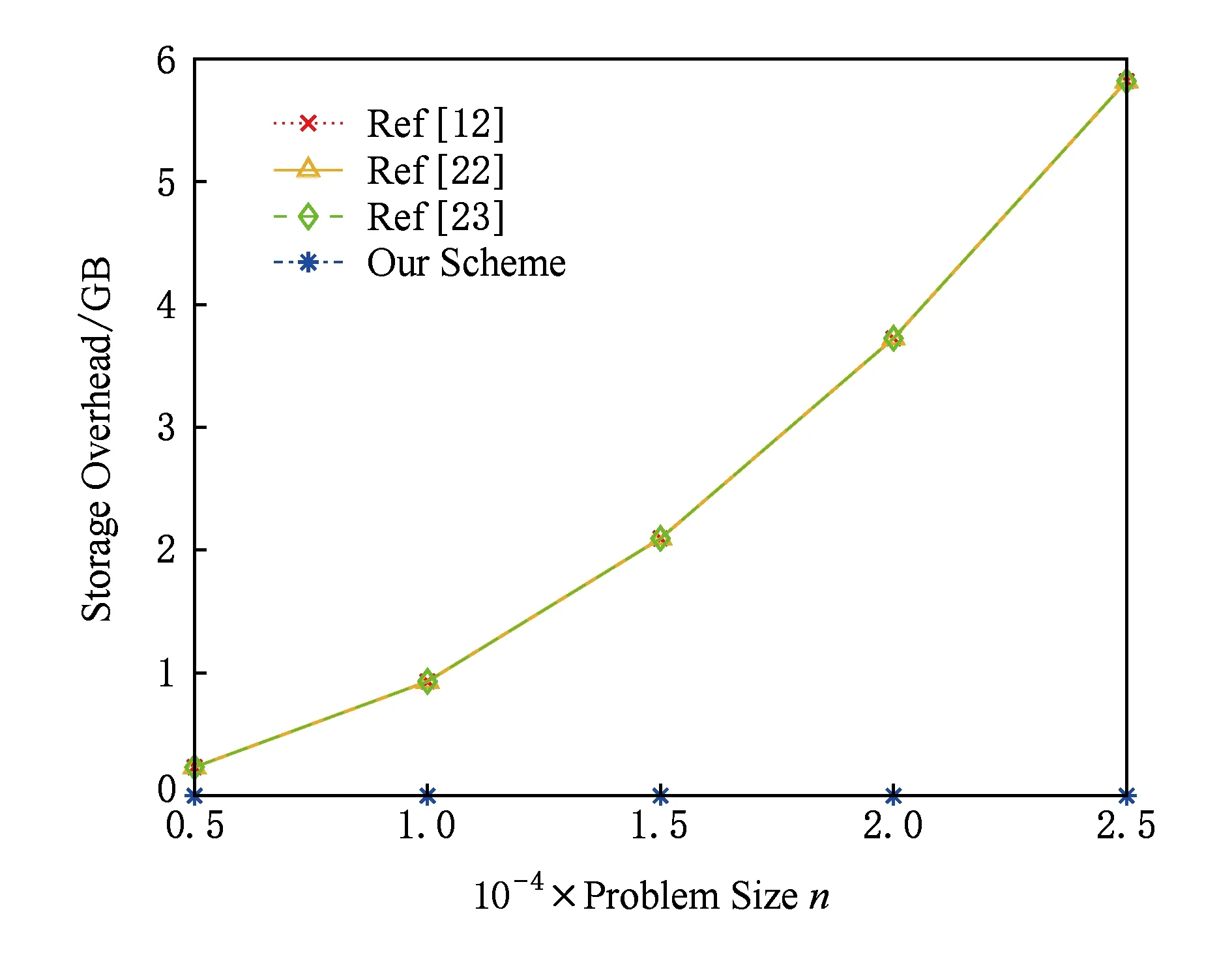
Fig. 5 Comparison for storage overhead图5 存储开销对比

以上结果表明:EVLE-LS方案优于之前的文献[12，22-23]中方法.

6 总 结

本文研究了安全外包大规模线性方程组问题.针对现有方案存在效率过低或存储开销过大等问题，构造了一种伪随机的稀疏严格对角优势矩阵生成算法，并基于该算法提出了一种新的外包大规模线性方程组方案.该方案取消了公钥，并大大降低了需要在客户端存储的私钥规模，具有高效率、低存储开销、完全可验证、无需与服务器进行多轮交互的优点.总体来说，该方案优于其他已有方案，对于存储能力有限的客户端安全外包大规模线性方程组问题具有一定理论指导和实际应用价值.