含惯性摆发电装置之浮标的水动力分析
王冬姣,王英毅,邱守强,刘 鲲,叶家玮,梁富琳
(华南理工大学 土木与交通学院,广州510640)
0 引 言
海上航标作为助航标志为海上船舶安全航行提供保障。目前普遍使用太阳能航标灯技术[1],即利用太阳能电池板给蓄电池充电,晚上通过光敏开关给灯器供电。针对现有太阳能航标灯连续二十几天阴天就可能导致亏电不亮,更换电池短时间需大量人力及物力,若因天气恶劣来不及更换将导致船舶事故的问题,因此本文提出在航标上增加一个惯性摆发电装置作为补充解决该问题。
目前已有的波力发电装置可分为振荡水柱式,越浪式和摇荡物体式三种类型[2]。振荡水柱式是利用气室内波浪相对于结构物的垂向运动,推动安装在气道中的涡轮机旋转,带动发电机发电。Masuda[3]成功地将振荡水柱式波力发电装置应用于海上航标,为其提供电力,这是目前为止波力发电装置最成功的应用例子之一。越浪式是将入射波聚集后通过坡道引入高于海面的蓄水池,利用蓄水池与海面之间的水位差直接驱动低水头水轮发电机组发电[4]。最简单的摇荡物体式波力发电装置是将一个浮标连接在固定结构物上,利用水面浮标和安装在海底固定结构物上的电力输出系统之间的相对运动发电[5]。这种装置的缺点是潮位适应性较差,因此更多的摇荡式波力发电装置是利用两个耦合物体之间的相对运动获取波能[6-8]。本文研究的含惯性摆发电装置之浮标是利用安装在浮标上的摆锤和浮标体之间的相对纵摇运动吸收波能。由于本文研究的浮标具有2 个对称面,浮标的垂荡运动与其它自由度的运动不耦合,横荡和横摇相互耦合,浮标体的纵荡、纵摇和摆锤的纵摇之间相互耦合。对波能转换有影响的主要是浮标体的纵荡、纵摇及摆锤的纵摇运动,因此本文主要研究这三个自由度的运动及负载阻尼系数对浮标纵摇运动,摆锤纵摇运动及波能转换效率的影响。
1 含惯性摆波能发电装置之浮标的物理模型
本文研究的含惯性摆发电装置之浮标的物理模型由下部浮标主体和上部发电模块组成。其中,浮标主体由圆柱形浮筒、立柱和压载环组成,见图1。浮筒为浮标提供浮力保障并为发电模块提供安装平台;压载环布置在立柱的下端,其目的是降低浮标的重心确保浮标满足稳性要求。图2 所示为上部发电模块,主要由支撑架、摆杆、摆锤、摆轴轴承以及发电机等组成。物理模型的压载环外径为0.12 m,厚度为0.08 m;立柱直径为0.08 m,高度为0.32 m;浮筒外径为0.30 m,浮筒吃水为0.091 m;浮标体(不计惯性摆)质量为8.26 kg,浮标体重心在水面之下0.149 m 处。惯性摆摆轴在浮标体重心之上的高度为0.555 m,惯性摆质量为0.26 kg,惯性摆重心离转轴距离为0.207 7 m,摆轴连接发电机,惯性摆相对于摆轴的惯性矩为0.013 1 kgm2。

图1 浮标主体Fig.1 Buoy hull

图2 发电模块Fig.2 Power generation part
物理模型实验在华南理工大学海岸与近海工程实验室波浪水槽进行。波浪水槽几何尺寸长×宽×高为30 m×1.0 m×1.5 m,可进行实验规则波和不规则波的模拟。图3 为放置在水槽中的物理模型,水深d=0.82 m。

图3 水槽中模型Fig.3 Configuration of experimental set-up in the wave flume
2 含惯性摆发电装置之浮标运动方程推导
2.1 坐标系及其转换
设在频率为棕,波幅为灼a的规则波浪作用下,浮标体在波浪中的摇荡运动为刚体6 自由度运动(j=1,2,…,6),另一个是惯性摆相对于铰接轴的纵摇运动(j=7)。为研究含惯性摆发电装置之浮标在波浪中的运动,须建立表达浮标及摆锤运动的坐标系,见图4。首先引入空间固定坐标系oxyz,原点o 设在未扰动的静水面上,oz 轴垂直向上;固连于浮标的坐标系Gxbybzb,原点G 位于浮标的重心,Gzb轴垂直于浮标水线面;固连于铰接轴的惯性摆坐标系o′x′y′z′,原点位于o′点。当浮标无摇荡运动时,o′x′轴与ox 轴及Gxb轴平行。浮标重心G 至水线面的距离为zG,以G 点位于水线面上方时为正。o′点垂向坐标zb=L。

图4 坐标系Fig.4 Coordinate system
设浮标上任意一点,它在固定坐标系下的坐标为(x,y,z),在浮标坐标系下为(xb,yb,zb)。由图4 可知,在波浪作用下,浮标体上任意一点M(xb,yb,zb)在固定坐标系下的位移可表示为

(1)式对时间求导,可得浮标体上任意一点M 在固定坐标系下的速度
设惯性摆坐标系原点o′点在浮标坐标系上的坐标为(0,0,zb=L),惯性摆只能在Gxbzb平面内摆动。浮标坐标系Gxbybzb与惯性摆坐标系o′x′y′z′之间的转换关系为

由(1)和(2)式可知,摆杆及摆锤上任一点p(x′,y′,z′)在固定坐标系下的位移可表示为

(3)式对时间求导,可得摆杆及摆锤上任意一点p 在固定坐标系下的速度
在微幅波假设下,浮标体及惯性摆作小幅值运动,有

2.2 浮标体及惯性摆系统具有的动能及势能
设浮标体的质量为Mb(不包括惯性摆系统),其质量分布为m(xb,yb,zb)。惯性摆系统由摆杆及摆锤组成,质量为Mp,其质量分布为m(x′,y′,z′),重心坐标位于(x′G=0,y′G=0,z′G)。浮标及惯性摆系统总质量为

系统的总动能由浮标体的动能及惯性摆的动能组成,可表示为

力学中势能由引力势能和弹力势能所组成。假设锚泊系统产生的恢复力是线性的,浮标体在j 自由度的运动引起在i 方向的锚泊刚度系数为KMij。Kp为与惯性摆相连的负载刚度系数。浮标体和惯性摆具有的引力势能(基准面取固定坐标系z=zG的位置)和弹性势能之和为

2.3 惯性摆结构阻尼耗散的能量及发电系统负载阻尼吸收的能量
惯性摆结构阻尼耗散的能量及发电系统负载阻尼吸收的能量可表示为

式中:C 为惯性摆的结构阻尼系数,ωpn为惯性摆的共振频率,ξ 为无因次阻尼系数,Bp为与惯性摆相连的负载阻尼系数。
2.4 流体对浮标体的作用力
(1)浮力及浮力矩
静浮时,浮标体及惯性摆的总重力等于作用在浮标体上的浮力

浮标体运动时作用在浮标体上的浮力及相对于浮标体重心G 的浮力矩为

式中:AWP为浮标体水线面面积,V0为浮标体静浮时的排水体积,zBG为浮标坐标系中的浮心垂向坐标。
(2)波向角为β 时由入射波势和绕射势产生的波浪扰动力
入射波波向角为β 时作用在浮标上的波浪扰动力可表示为

式中:Ei0为单位波幅产生的波浪扰动力幅值,ζa为波幅。
(3)辐射流体动力载荷
将浮标运动时遭受的辐射力分解为与浮标运动加速度和速度成比例的两部分,即

式中:Aij为浮标体的附加质量,Bij为辐射阻尼系数。
借助于商业软件AQWA-LINE[9]计算浮标体的附加质量、辐射阻尼系数及作用在浮标体上的波浪力及力矩。
2.5 含惯性摆发电装置之浮标的运动方程
由拉格朗日运动方程[10]

可得含惯性摆发电装置之浮标的运动方程

式中:质量矩阵为
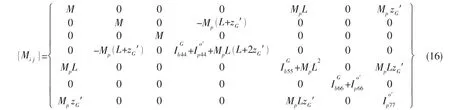
附加质量矩阵为

辐射阻尼系数矩阵为

结构阻尼及负载阻尼系数矩阵为

由静水压力及质量分布引起的刚度矩阵

式中:

负载刚度矩阵为

浮标在运动过程中,特别是横摇和纵摇运动,其粘性阻尼是不可忽略的。在共振周期附近,与辐射阻尼相比粘性阻尼起主要作用。因此在(15)式中需要将粘性阻尼项加入运动方程中。
由横摇/纵摇产生的粘性阻尼力矩可表示成[11]

式中:

取Cd=2。
为了考虑波浪频率对纵/横摇非线性粘性阻尼的影响,参考文献[12]的思路,将(24a)式修改为

在频域运动中需要对非线性粘性阻尼进行线性化,在规则波中有

3 波能转换效率

式中:ω 为波浪圆频率,k0为波数,d 为水深,波高H=2ζa。
浮标重心G(不含惯性摆)处的摇荡运动及惯性摆的纵摇运动可表示为

式中:ηj0(j=1,2,…,7)为复数振幅。
波能转换系统负载阻尼吸收的平均功率为

波能转换效率η 可表示为

4 结果与分析
4.1 无负载阻尼时理论计算与实验结果的比较
取波高H=2ζa=3 cm,波向角β=0°,忽略锚泊系统对波频运动的影响,利用数值计算方法得到无负载时浮标纵荡运动、纵摇运动及摆锤相对于浮标的纵摇运动与实验结果的比较见图5~7。若浮标固定不动时,则摆锤具有一个固有周期。若将摆锤锁住,浮标纵摇运动也具有一个固有周期。由于浮标纵摇运动和摆锤的纵摇运动之间是相互耦合的,使得浮标和摆锤的纵摇运动具有两个固有周期,一个靠近浮标固定不动时摆锤的固有周期,另一个靠近摆锤锁住时浮标纵摇运动的固有周期。计算中如果不考虑浮标纵摇非线性粘性阻尼的影响,在浮标纵摇共振周期附近不但浮标的纵摇运动响应很大,摆锤的纵摇运动也很大,而浮标的纵荡运动响应曲线则存在突变现象,即随着波浪周期变长,在浮标纵摇固有周期附近浮标纵荡运动响应曲线先逐渐减小然后从最小值突然增加到一个最大值后再逐渐减小回归到实际应有的曲线。在方程中考虑浮标纵摇运动非线性粘性阻尼的影响后,在浮标纵摇固有周期附近浮标的纵荡运动曲线变得较为平滑,不存在突变现象,而浮标的纵摇运动及摆锤的纵摇运动幅值将大幅减小。在摆锤共振周期附近,不但摆锤的相对纵摇运动有极大值,浮标的纵摇运动也有极大值,考虑浮标纵摇的非线性粘性阻尼后,峰值将大幅减小。浮标纵荡运动响应曲线在摆锤共振周期附近,随着周期变长,曲线先逐渐增加到极大值时迅速降低到最小值后再逐渐增加回归到实际的曲线。考虑浮标纵摇的非线性粘性阻尼后,浮标纵荡运动的突变依然存在,但变化幅度降低。由图可知,考虑粘性阻尼后计算得到的运动响应曲线和实验结果是比较吻合的。在摆锤共振周期附近,摆锤相对纵摇运动曲线的计算与实验结果的差别较大,这里除了与纵摇的非线性粘性阻尼有关外,还应与摆锤的非线性结构阻尼有关。

图5 浮标体纵荡运动响应理论与实验结果比较Fig.5 Comparison of theoretical and experimental results for surge response of the buoy

图6 浮标体纵摇运动响应理论与实验结果比较Fig.6 Comparison of theoretical and experimental results for pitch response of the buoy
4.2 负载阻尼系数的影响

图7 摆锤相对纵摇运动响应理论与实验结果比较Fig.7 Comparison of theoretical and experimental results for relative pendulum response

图8 负载阻尼系数对浮标纵摇运动的影响Fig.8 Influence of the power take-off damping on pitch RAOs of the buoy

图9 负载阻尼系数对摆锤纵摇运动的影响Fig.9 Influence of the power take-off damping on pendulum RAOs

图10 负载阻尼系数对摆捶相对纵摇运动的影响Fig.10 Influence of the power take-off damping on relative pendulum RAOs

图11 负载阻尼系数对波能转换效率的影响Fig.11 Influence of the power take-off damping on wave energy conversion efficiency
取H=3 cm,茁=0°,负载刚度系数KP=0,负载阻尼系数Bp对浮标和摆锤运动响应及波能转换效率的影响如图8~11 所示。由图8 可知,在所计算的波浪周期范围内,浮标的纵摇运动曲线存在两个峰值区和一个谷值区。在谷值区浮标的纵摇运动幅值随着负载阻尼系数的增大而增大,在峰值区则随之减小。由图9~11 可知,对于摆锤纵摇、摆锤相对纵摇运动及波能转换效率的峰值主要发生在摆锤固有周期附近。而在浮标纵摇固有周期附近,尽管浮标纵摇的运动响应较大,但摆锤的相对运动幅值较小且长周期对应的入射波平均功率较大,因此波能转换效率很低。由图11 可知,负载阻尼系数Bp较小时,波能转换效率随负载阻尼系数的增加而增大,负载阻尼系数Bp=0.006 Nms/rad 时,最大波能转换效率达到32.1%,负载阻尼系数继续增大,其波能转换效率的峰值将降低。负载阻尼系数较小时,波能转换效率为窄而高的曲线。负载阻尼系数Bp>0.006 Nms/rad 时,随着负载阻尼系数的增大,曲线峰值降低但峰值两侧的波能转换效率随之增大。
5 结 论
本文利用拉格朗日方程详细推导了含惯性摆发电装置之浮标在波浪作用下的运动方程,计算了浮标及摆锤在规则波作用下的运动响应,并与实验结果进行了比较,两者吻合良好,说明本文推导的七自由度运动方程是正确的。
在固有周期附近,浮标纵摇非线性粘性阻尼的影响非常明显,须加以考虑才能得到合理的计算结果。在摆锤固有周期附近能获得较大的波能转换效率,而在浮标纵摇固有周期附近的波能转换效率则较低。浮标的纵摇运动曲线存在两个峰值区和一个谷值区,在谷值区浮标的纵摇运动幅值随负载阻尼系数的增大而增大,在峰值区则相反。摆锤的相对摆幅随负载阻尼系数的增大而降低。负载阻尼系数很小时波能转换效率曲线随负载阻尼系数增大而增大;负载阻尼系数较大时波能转换效率从窄而高的曲线向宽而峰值低的曲线变化。

