基于EMD-ICA的心冲击信号降噪研究

姜 星 耿读艳，* 张园园 付志刚

1(河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130)2(河北工业大学河北省电磁场与电器可靠性重点实验室，天津 300130)3(中国人民解放军第254医院，天津 300142)

引言

心冲击图(ballistocardiogram，BCG)可以展示心脏搏动和血液在大动脉流动而引起的人体对外压力或体表位移的变化，反映心脏的力学特征[1]，通过压力、加速度、电容等传感器来感知身体的这种微小位移变化，从而获取心脏搏动引起的体震信息。正常的BCG信号波形及其生理意义如图1所示，主要包含H、I、J、K、L、M和N等7种波形，其中I、J、K反映心动周期的射血过程，而L、M、N反映舒张过程[2]。相比Holter等心电监测方式，BCG可实现更长期的连续监测，避免电极及其导线束缚造成对人情绪的影响，尤其适合于长时间作息和睡眠监测，比较适用于家庭应用。然而，BCG信号自身十分微弱，且易受到呼吸、体动、工频噪声的干扰[3-4]，导致直接测量得到的BCG信号含有太多噪声，不能直接获得准确的生理信息特征。因此，BCG的降噪处理显得尤为必要。

图1 正常BCG信号波形及其生理意义Fig.1 Normal BCG signal and physiological significance

目前对于BCG信号的降噪处理主要是采用小波变换方法，一般是对周期性平稳信号有效，而对包含尖峰或突变的非平稳信号效果不佳[5-6]。小波降噪能同时进行时频分析，且能有效区分非平稳信号的尖峰与噪声，但需选取合适的小波基才能达到较好降噪效果，而小波降噪仍基于Fourier变换，尚不能摆脱以Fourier变换为基础带来的缺陷[7-9]。经验模态分解(empirical mode decomposition, EMD)是Huang在1998年提出的一种用于非线性和非平稳时间序列信号的处理方法[10]，主要是将信号分解为若干个固有模态函数(intrinsic mode function, IMF)分量，使每个IMF包含不同的频率成分，从而实现信号特征的有效分解。但是在分解过程中，由于BCG信号中有大量噪声成分，存在较强的时频耦合特征，会产生模态混叠现象[11]，造成IMF成分中包含不同的时间尺度，从而对各个模态分量的物理意义判别造成困难。独立分量分析(independent component analysis, ICA)无需信号源先验知识，在时域和频域都能将观测得到的混合信号中的独立成分分离出来。ICA去噪的关键点在于噪声通道的构建，孙云莲等利用EMD分解得到的IMF希尔伯特时频谱来构建噪音通道，在信噪比较高的情况下，基于IMF时频谱分析的ICA降噪法取得了不错的效果[12]。本研究在其基础上，提出一种基于EMD及ICA相结合的BCG信号降噪方法。该方法对含噪BCG信号进行EMD分解，得到频率从高到低的多个IMF；通过引入模态相关法，找到噪声与信号的分界IMF；对分界之前的分量构建虚拟通道[13]，与原信号一起作为ICA的输入，得到降噪后BCG信号。

1 方法

1.1 信号采集系统

在本研究中，使用的是自主研制的BCG信号采集系统，主要由采集人体信号的压电薄膜式传感器、连接传感器对采集信号做后续处理的电路和上位机软件组成。将传感器置于座椅坐垫下，受试者静止地坐在座椅上，心脏射血时引起身体微小振动，通过传感器获取射血引起的重力变化信号[14]，经过电路的多级放大和转换，将其无线传输到上位机软件，最终得到测量的BCG信号。采集电路主要包括电荷放大器、低通滤波器、电压放大器、电压抬升电路、信号离散模块、无线传输模块和串口通信，其总体构成如图2所示。

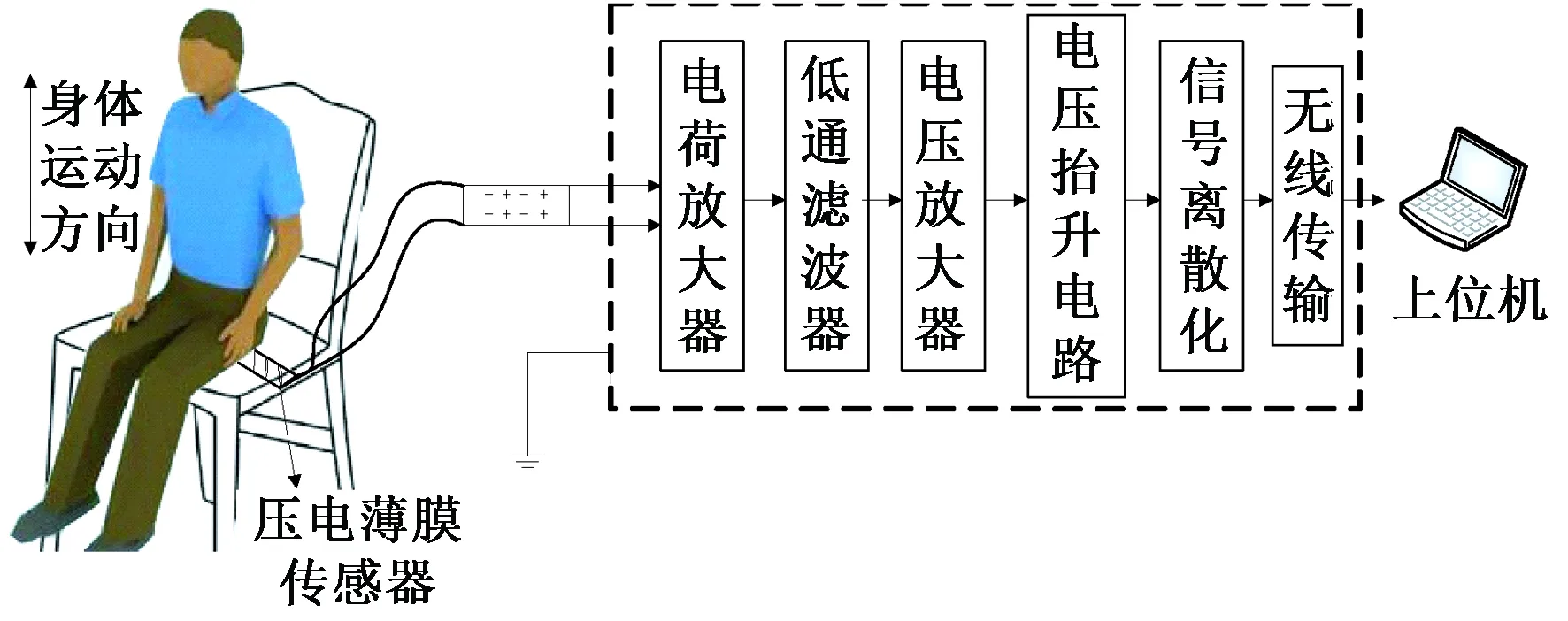
图2 电路整体设计框图Fig.2 Overall design circuit diagram

1.2 EMD-ICA原理

经验模态分解的实质是对一个时间序列信号进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解，产生一系列具有不同特征尺度的数据序列，每一个序列称为IMF。分解得到的IMF必须满足两个条件：一是IMF中极值点的个数与过零点的个数相等或不超过1个；二是由极大值与极小值确定的包络线均值为0。

独立分量分析是由盲源分离计算发展起来的一种信号处理方法，要求输入的是多维信号，并且混合信号个数要大于等于源信号个数，才能有效地分离。

由独立分量分析的原理可知，独立分量分析要求输入的是多维信号，并且混合信号个数要大于等于源信号个数，才能有效地分离。基于此，BCG信号经EMD分解后产生若干个基本信号，即

(1)

式中，x(t)表示原始信号，imfi表示第i个IMF分量，rn(t)表示余项。

提取出噪声所在的IMF分量进行组合，得到噪声的估计量；与源信号一起作为ICA多维噪声输入，构建ICA噪声通道。本研究采用基于EMD模态相关分选准则[15]判定噪声与信号的分界层，计算模态函数与原始BCG信号之间的互相关系数，有

(2)

图3 EMD-ICA降噪原理Fig.3 EMD-ICA de-noising principle

1.3 信号采集过程

本研究为了验证所得到的BCG信号的准确性，使用ECG-300 A数字式三道心电图机和所设计的BCG采集系统，同步采集被试者的ECG和BCG信号，并实时保存。对所采集的BCG信号分析得到心率，并与心电图机所得心率进行对比，分析BCG的准确性。

为了验证装置的有效性，并对人体心冲击信号的特征进行研究，本研究共采集了10位健康成年人的数据，其中有5位男性、5位女性，年龄均在23～27岁。要求受试者保持平稳的坐姿，坐在放有压电薄膜传感器的座椅上，匀速呼吸，将传感器的输出端接在信号调理电路上，使用示波器观察其BCG信号，等待信号稳定后采集2 min的BCG信号，同时采集被试者的ECG信号。将采集到的数字信号经过Matlab处理后得BCG的原始信号，图4为某一被试者采集的原始BCG信号。

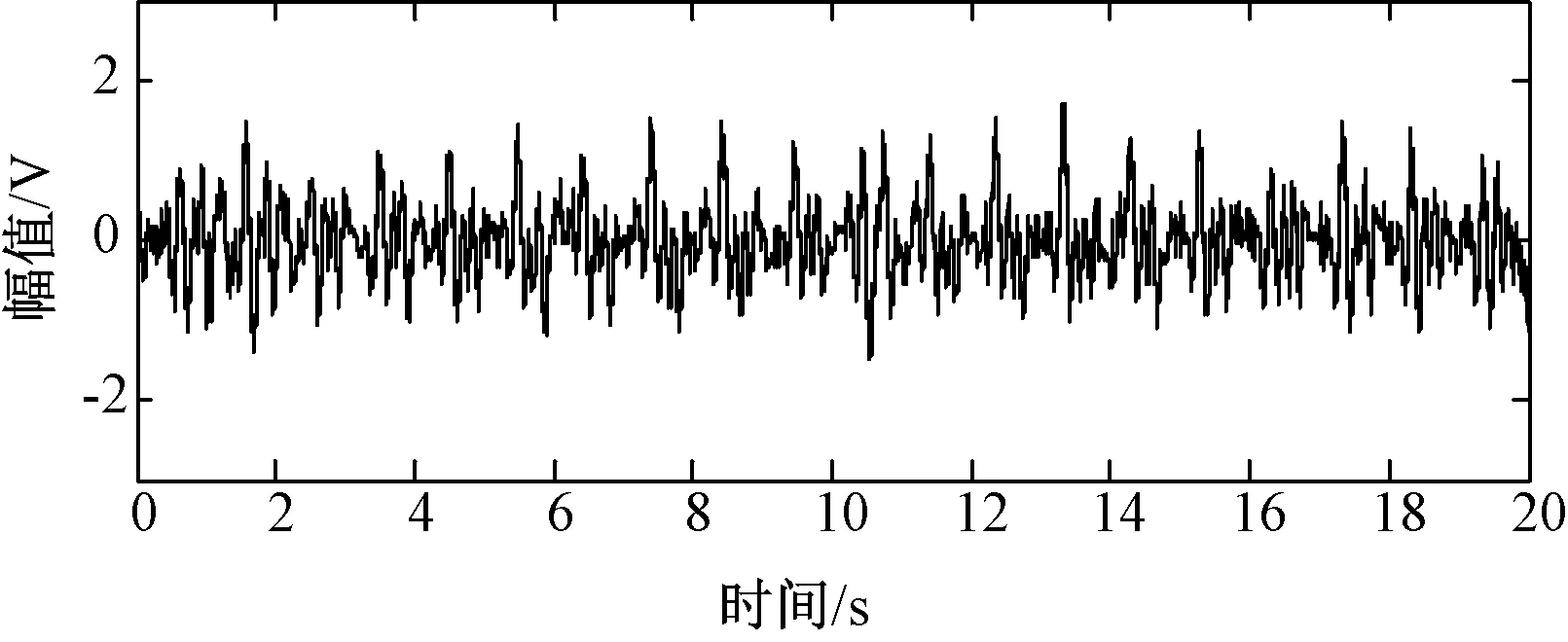
图4 原始BCG信号Fig.4 Example of the original BCG signal

由图4可见，BCG信号中可以明显观察到J峰，同时可以看到BCG信号的I、J、K波形是有重复性的，所以表示所采集的BCG信号是具有鲁棒性的。另外，不同的被试者BCG信号的波形形状和幅度存在着较大的差别，这些差别来源于每个人不同的心脏活动状态以及身体结构。

1.4 信号处理

将采集到的BCG信号进行EMD分解，结果如图5所示。

图5 EMD分解结果Fig.5 EMD decomposition results

由分解结果可以看出，原始信号经EMD分解得到了几个固有模态分量和一个趋势项。由EMD分解过程可知，分解得到的13个IMF分量imf1，imf2，…，imf13中，噪声对每个IMF分量的支配作用逐渐降低，信号对IMF的支配作用不断加强，因此需要确定IMF分量中信号与噪声的分界[16]。根据式(1)计算出各阶固有模态分量与原始BCG信号的相关系数，得到结果后绘制相应的曲线，如图6所示。

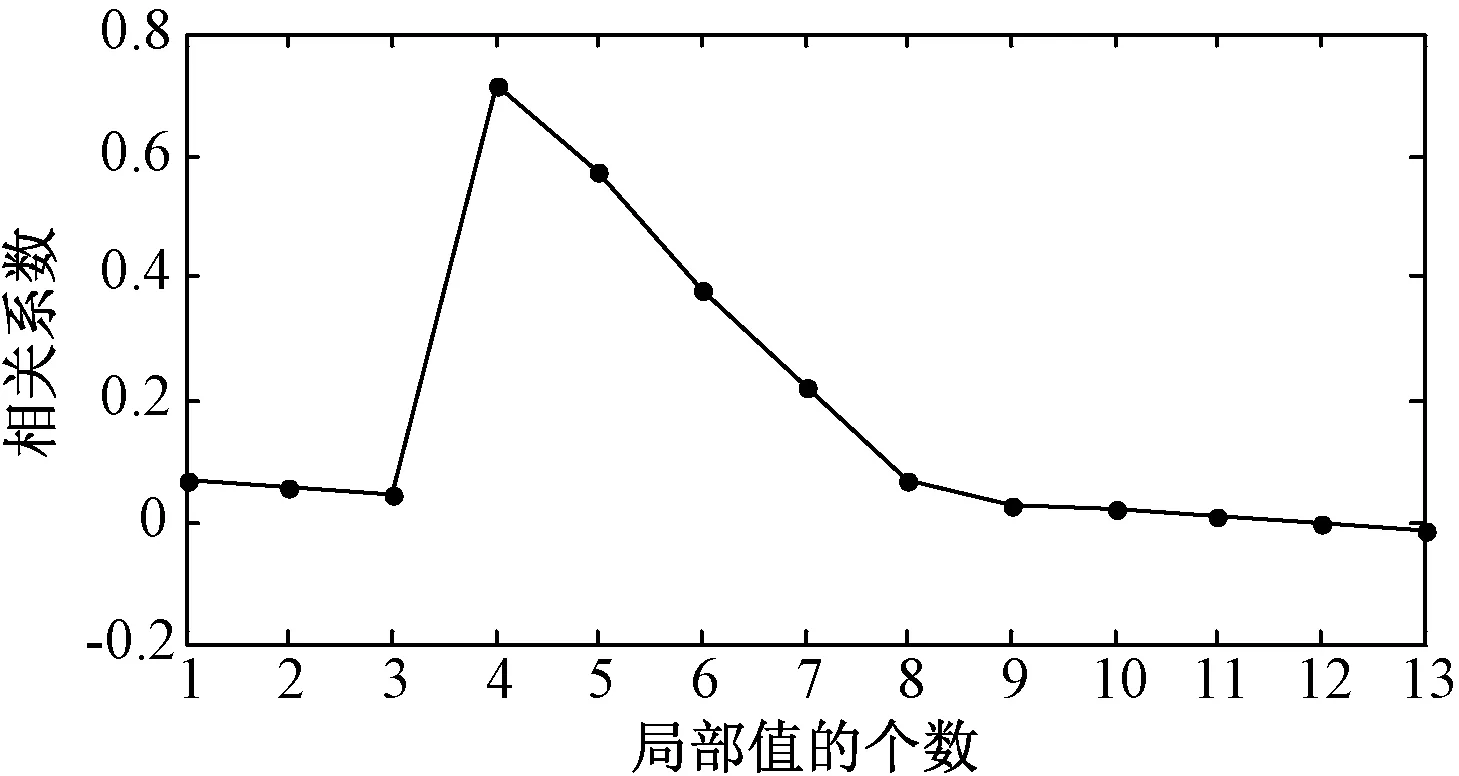
图6 相关系数曲线Fig.6 The correlation coefficient curve table

按照前述信号与噪声的分界点判定方法，由图6可以看出，imf4为分界IMF。根据噪声与信号的分界，选择第1～3个IMF分量作为虚拟噪声通道。由于原始BCG信号进行EMD分解后imf4之前的IMF分量大都是噪声成分，所以借鉴信号时序平移思想构造ICA的多维输入[17]，其基本思想是：把原始BCG信号分解后得到的由第1～3个IMF分量构建的虚拟噪声通道时序序列向左平移l个位置，向左溢出部分拼接到该时序序列的右端，这样就可以得到新的含噪信号作为ICA的噪声通道输入。这个新的含噪信号与原信号相比信噪比几乎一致，不仅保留了原信号中的有效成分，而且信号中含噪声的成分也没有大的改变，仅是噪声形态发生了改变。

这样就构造了多个输入信号，包括两个虚拟噪声通道和原始BCG信号。在独立分量分析中，常用的算法是Fast ICA和Infomax算法，从计算速度方面考虑，本研究采用一种基于负熵的判据和一种非常高效的FastI CA[18-19]算法进行分析，其框图如图7所示。负熵定义如下：

(3)

式中，E为均值运算，g为非线性函数，Ygauss是高斯变量。Fast ICA其步骤如下：

1) 对观测信号进行中心化处理，使其均值为0。

2) 利用特征值分解法对中心化后的数据进行白化，得到标准化数据Z(t)。

3) 选择要估计的独立成分个数m，迭代次数为p，初始值为p=1。

4) 选择一个随机的初始分离矩阵W。

5) 迭代更新分离矩阵，令

(4)

(5)

Wp=Wp/‖Wp‖

(6)

式(4)中,g(y)=tanh(a1,y),a1=1。

6) 判断Wp是否收敛，如果不收敛，返回步骤5)。

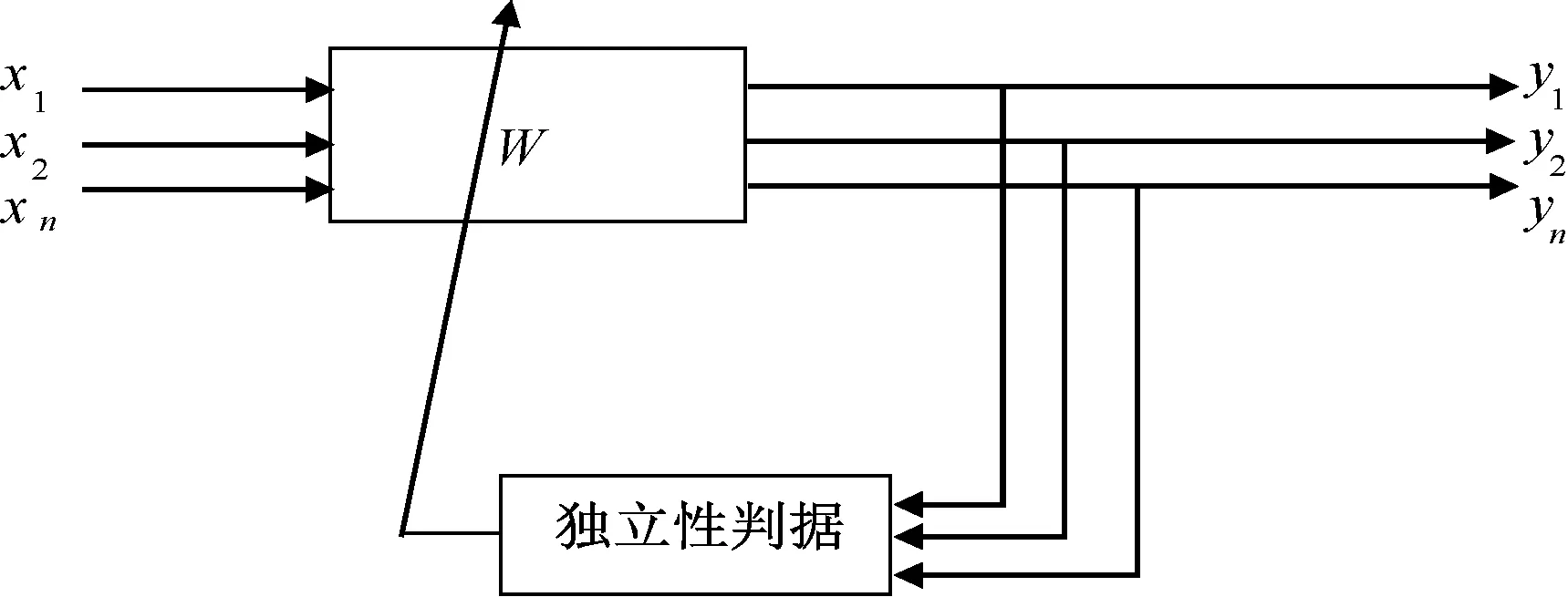
图7 Fast ICA算法框图Fig.7 Fast ICA algorithm block diagram

7) 令p=p+1，假如p≤m，返回步骤4)，重复执行步骤4)～7)，直到将所有需要的独立分量提取出来为止，算法结束。

1.5 算法性能评价

为了定量说明本方法的降噪效果，同时采用EMD方法和小波去噪方法[20]，分别对本研究的含噪BCG信号进行降噪处理，比较不同方法的降噪效果。为了定量分析3种方法的降噪效果，计算其降噪后信号与原始信号的相关系数(R值)、信噪比(Rsn值)和能量比(Esn值)。相关系数值说明了降噪后的信号与原始信号之间整体波形的相似度，信噪比说明了信号的去噪情况，而能量比值反映了降噪后信号占原信号的能量百分比。其中，信噪比Rsn定义[21]为

(7)

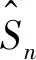
若降噪后信号具有较高的信噪比，说明降噪效果好。

信号能量计算公式[16]如下：

(8)

式中，x(t)为信号幅值，T为采样周期，m为采样点数。

降噪后的信号占原信号的能量百分比Esn定义为

Esn=E0/E

(9)

式中，E表示原始信号能量，E0表示降噪后信号能量。

Esn越大，说明降噪后的信号越高，越能保持原信号特征，也越接近原信号。

2 结果

2.1 采集系统

为了验证信号采集系统的准确性，经过心冲击图和心电图方法计算得出心率[22]，如表1所示。对其用配对t检验方法进行检验，结果显示两种方法计算得出的心率不具有显著性差异(P>0.05)，说明本研究的BCG采集系统具有一定的准确性。

表1 被试者的心率计算结果

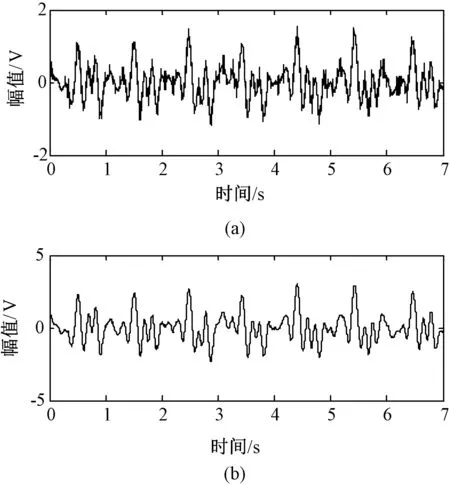
图8 BCG信号降噪前后对比。(a)降噪前BCG信号；(b)降噪后BCG信号Fig.8 BCG signal de-noising before and after the comparison. (a) Noise reduction before BCG signal；(b) Noise reduction after BCG signal

2.2 降噪效果

根据上述的分析方法，由Fast ICA最终得到降噪后的BCG信号。图8所示为BCG信号降噪前后的波形，可以观察到降噪处理后BCG的信号特征得到了明显的保留，信号波形较之前也趋于平滑。为了进一步证明降噪效果，计算了降噪前后BCG信号的功率谱密度(power spectral density，PSD)，如图9所示。可以看出，在高频部分BCG信号功率谱明显趋于平滑，且在低频部分没有明显的衰减，进一步说明本研究采用的方法在去除噪声的同时，很好地保留了BCG信号的低频特性。

利用算法评价指标，分别计算10名被试的原始BCG信号降噪前后的相关系数、信噪比、能量百分比，得到的结果如图10所示。对其进行单因素ANOVA检验，结果显示3种降噪方法计算得出的相关系数、信噪比、能量比具有显著性差异(P<0.05)；并计算其平均值，结果如表2所示。

表2 不同降噪算法效果对比Tab.2 Comparison of different noise reduction algorithms

图9 降噪前后BCG信号的PSD。(a)降噪前；(b)降噪后Fig.9 PSD before and after de-noising BCG signal. (a) Before de-noising；(b) After de-noising

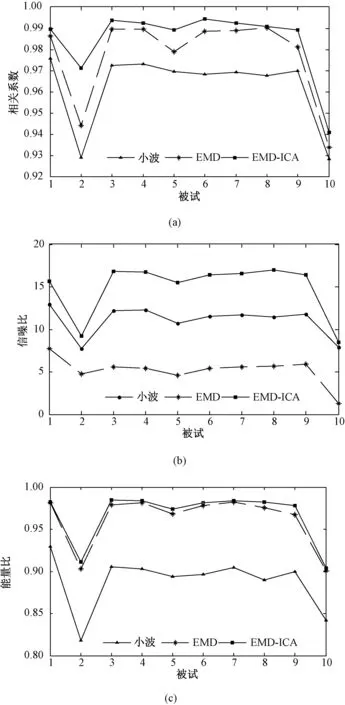
图10 不同降噪方法处理前后的对比。(a)相关系数对比；(b)信噪比对比；(c)能量比对比Fig.10 Comparison of quantitative figure before and after different noise reduction methods. (a) Comparison of correlation coefficient；(b) Comparison of signal-to-noise ratio； (c) Comparison of energy percentage

由图10可以看出，EMD-ICA方法得到的相关系数、信噪比和能量百分比的各项指标均优于小波和EMD方法的指标。如表2所示，对其进行配对t检验，EMD-ICA相比EMD方法信噪比显著提高(5.19±1.29vs14.87±3.04，P<0.001)，相比小波方法能量百分比显著提高 (88.81±2.81vs96.64±2.92，P<0.001)。虽然小波降噪方法的信噪比较高，但是相关系数和能量百分比相对于其他两种方法最低。EMD降噪方法虽然相关系数和能量百分比相对较高，但是信噪比相比其他方法最低。3种方法比较来看，小波降噪方法的降噪效果虽较好，但也损失了部分原信号的信号特征；EMD降噪方法能较好地保持原信号特征，接近原信号，但降噪效果不明显；EMD-ICA降噪方法的降噪效果最明显，最大限度地保留了原信号的信号特征。

3 讨论

消除噪声是BCG信号预处理的重要内容，由于采集系统和外部环境等因素的影响，采集的BCG信号数据含有不同类别的噪声，具有非线性、非平稳性，严重影响心率等生理信息测量的准确性。综合考虑降噪效果和计算量，本方法避免了文献[23]中需要大量实验确定小波基与分解尺度的问题。从信号分解角度，小波变换中基函数是固定的，不能匹配信号的全部，用自适应EMD分解方法代替复杂的小波变化，大大降低了算法的复杂度。文献[14]中EMD分解BCG信号确定IMF阶数后，直接对各分量进行重构，不能有效消除IMF中由于高频噪声的干扰以及时间尺度信号变化等因素引起的模态混叠噪声。本研究提出信号时序平移方法构造多个观测信号，通过ICA可以实现混叠频率的有效分离，从而估计出IMF中的原始信号，能有效消除EMD分解过程中模态混叠现象对降噪结果的影响，提高降噪效果。

EMD方法因在处理非线性、非平稳信号上的优越性而得到了广泛的应用，能够自适应地分解信号，但其分解过程中面临的端点效应问题阻碍了其发展。对于该问题，目前提出的很多方法都是从算法上入手来抑制端点效应的影响，忽略了噪声信号在EMD分解过程中对端点效应的影响。本研究选择增加BCG信号长度，以减少端点效应对信号降噪的影响。此外，分离信号的幅度和顺序上存在不确定性，但是BCG信号的特征存在于相对幅频特征中，因此对BCG信号的研究影响不大。

由于压电薄膜传感器的测量原理，BCG信号极易受到身体晃动的干扰，咳嗽、扭动身体等引起的轻微运动都会影响信号的质量，使得特征难以辨认，不能有效地提取信号。本系统目前适用于安静状态下获取BCG信号，比较适合睡眠时检测，特别适用于家庭应用。因此，未来工作首先要解决BCG信号在各种条件下的采集与降噪问题，以保证BCG信号的质量。其次，随着对BCG信号生理意义研究的不断深入，希望探求一种既能代替心电图实现多参数无感检测又可以将BCG信号包含的心血管系统生理信息用于辅助医生的方法，从而对各种心血管疾病进行诊断与分析。这是今后研究的方向，其实现将有力于促进人类健康水平的提高。

4 结论

本研究综合考虑EMD与ICA的技术优点，提出一种基于EMD-ICA的BCG信号降噪方法。该方法利用EMD将BCG信号分解，根据模态相关准则将分解信号进行信号层与噪声层的判定，得到重构信号并作为ICA的输入，最后去除了原始信号中的噪声成分。该方法克服了EMD分解过程中产生的模态混叠问题，同时解决了ICA方法中多维输入的要求，实现了多周期BCG信号的降噪。通过与小波和EMD降噪方法进行对比实验研究，表明该方法能够更有效地识别心脏的动力学信号，这对后期研究日常作息条件下与人体健康状态相关的生理病理信息有重要意义。