基于3D-VCCT的多裂纹输气管道断裂分析方法

姚安林 赫文博 徐涛龙 蒋宏业 谷东方

1.西南石油大学石油与天然气工程学院 2.油气消防四川省重点实验室

0 引言

油气管道在制造、安装或服役过程中不可避免地会产生裂纹缺陷，这些缺陷有时是以多裂纹的形式存在的[1]。GB/T 19624—2004《在用含缺陷压力容器安全评定》在一定条件下采用包络合并准则将相邻裂纹合并成一个裂纹再进行安全评定，而相关研究[2]认为包络合并准则不能准确反映裂纹间的干涉影响，从而使得评定结果偏于保守。

目前，国内外学者对管道裂纹已开展了一定研究。Kumar等[3]以管道周向裂纹为研究对象，开展管道裂纹尖端应力强度因子（K）的研究；Jacquemin等[4]针对管道焊缝错位裂纹，分析了裂纹深度和焊缝错位值对断裂参量J积分的影响；Arafah等[5]以厚壁管道为研究对象，开展双轴拉伸弯曲载荷试验，证明了预测临界载荷和试验所得载荷的吻合性。宋汉成等[6]借鉴管道轴向裂纹和环向裂纹的评估方法，提出了基于应力投影的螺旋裂纹评估方法；白永强等[7]通过对输气管道裂纹扩展因素进行分析，发现管道内压对裂纹驱动力的影响最大，但以上研究均是基于单裂纹缺陷。而相对于单裂纹缺陷，管道多裂纹缺陷的建模难度更大、干涉机理更复杂，目前仅有少数学者进行了研究，何雪等[8]将含双轴向裂纹缺陷的管段简化为二维模型，讨论了裂纹夹角对应力强度因子的影响，但该研究工作未对简化模型的合理性作出解释。综上所述，针对输气管道多裂纹干涉效应的研究相对较少且不成熟，因此有必要继续开展此类研究，以期提高含缺陷输气管道安全评估的准确性。

以断裂力学为基础的失效评估图（Failure Assessment Diagram，FAD）为含裂纹缺陷构件的安全评定提供了新的途径，其中K是运用FAD评估裂纹缺陷的重要断裂参量之一[9]。鉴于此，首先引入奇异单元法和3D-VCCT的理论模型，给出K的计算方法；其次，在对比奇异单元法和3D-VCCT的基础上，优选3D-VCCT建立输气管道多裂纹干涉模型；最后，通过分析裂纹相互干涉作用因子（η）的变化，研究附属裂纹对主裂纹的干涉效应，从而为后续建立更精准的多裂纹安全评定模型提供技术指导和参考数据。

1 基本理论

对于承受内压的输气管道而言，由环向应力引起的张开型（Ⅰ型）断裂相对较为严重，故以轴向半椭圆裂纹为研究对象。目前K的计算方法主要有解析法、试验法和数值法，其中解析法只能求解特定几何形状和荷载的单裂纹问题，试验法虽可以求解K，但成本较高[10]。相比于解析法和试验法，数值法在断裂问题的求解过程中受到越来越多学者的青睐，其中3D-VCCT和奇异单元法是两种重要的方法。

1.1 3D-VCCT理论模型

针对一个厚度为B的平板线状裂纹，Irwin[11]提出能量释放率（G）的概念，其定义为裂纹扩展（Δc）产生新裂纹面所需要的能量。对于Ⅰ型裂纹，其表达式为：

式中GI表示Ⅰ型裂纹的能量释放率，N/mm；W表示外力做功，N·mm；B表示厚度，mm；Δc表示裂纹扩展量，mm；σ表示应力，N；u表示竖向（Y轴）距离，mm；r表示距裂纹尖端的距离，mm。

式（1）涉及沿着闭合裂纹线对应力的积分，而在有限元分析中虚拟裂纹线上应力做功等于节点力在节点位移上做功，Ⅰ型能量释放率可以通过结点力与节点位移计算得到，其表达式如下：

式中u1,2表示节点1与节点2在竖向的位移变化，mm；Fy5表示节点5的节点力，N。

相对于线状裂纹，面状裂纹[12]由裂纹前缘而不只是一个点（线状裂纹的裂纹尖端）来描述，因此Ⅰ型能量释放率的计算相对更加复杂。有限元分析中面状裂纹八节点单元的能量释放率计算公式如下[13]：

式中 表示i单元的Ⅰ型能量释放率，N/mm；wi表示i单元的裂纹前缘长度，mm；F1、F2分别表示节点力，N；u1、u2分别表示节点的位移变化量，mm；C1、C2分别表示系数；wi-1表示i-1单元的裂纹前缘长度，mm；wi+1表示i＋1单元的裂纹前缘长度，mm。

对于平面应变问题，应力强度因子与能量释放率存在如下关系：

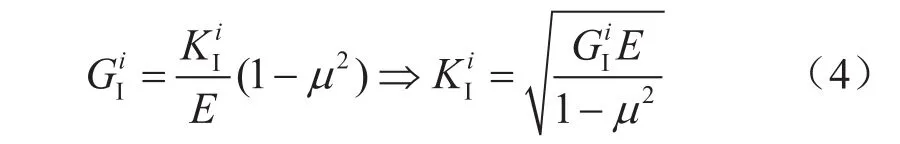
式中E表示弹性模量，MPa；μ表示泊松比； 表示i单元的Ⅰ型应力强度因子，MPa·mm1/2。

1.2 奇异单元法理论模型

Henshell和Shaw[14]于20世纪70年代中期提出了奇异单元理论，奇异单元是绕裂纹尖端附近构造的一种特殊单元，可反映裂纹尖端应力应变的奇异性。对于平面应变状态，Shih等[15]证明了裂纹尖端Ⅰ型应力强度因子可通过下式求得：

式中r1/4表示1/4节点到裂纹尖端的距离，mm；v1/4表示1/4节点处裂纹的张开位移，mm。奇异单元的节点位置如图1所示。

图1 奇异单元的节点位置图

图2 输气管道裂纹几何模型图

2 管体三维半椭圆裂纹模型

2.1 几何模型及参数设定

输气管道裂纹几何模型如图2所示，选取管长（L）为2 000 mm，壁厚（t）为17.5 mm，内径（R）为490.5 mm，均布内压载荷（p）为10 MPa的X70管线钢为研究对象[16]，其力学参数为：泊松比0.3；密度7 900 kg/m3；弹性模量210 GPa。图2-b给出了平行共线、平行共轴和平行偏置3种位置关系的多裂纹几何模型。设定主裂纹长半轴为c，短半轴为b，裂纹前缘与内壁夹角为θ，θ＝0°为近表面点，θ=90°为最深点，θ=180°为远表面点，远表面点与近表面点统称为表面点，附属裂纹长半轴为ci，短半轴为bi，主裂纹与附属裂纹最深点的水平间距为Li，最深点的竖向间距为βi，i=1表示平行共线位置，i=2表示平行共轴位置，i=3表示平行偏置位置（图2-b）。

2.2 有限元模型建立

基于ABAQUS有限元软件，运用奇异单元法和3D-VCCT建立管道三维有限元模型，模型两端施加固定约束，为消除边界条件对裂纹前缘应力分布的影响，半椭圆裂纹预制在管道的中间位置，并在管道内壁和半椭圆裂纹面分别施加内压载荷10 MPa。值得注意的是，使用有限元软件计算K需要对裂纹面做出合适的几何切分以便划分出特定的裂纹网格，考虑到奇异单元法中与裂纹前缘相接触的单元需采用奇异单元，故裂纹面切分、扫略（图3-a），而3D-VCCT无需考虑裂纹单元的奇异性，裂纹面切分如图3-b所示。此外，有研究[17]提到裂纹网格尺寸影响求解应力强度因子的精度，为此对裂纹前缘两侧的区域分别进行网格加密处理，网格划分均采用八节点六面体全积分单元，对应的有限元单元类型为C3D8，奇异单元法和3D-VCCT法裂纹前缘（黄色线条）两侧各加密6层的网格模型如图4所示。

3 数值模拟与结果分析

3.1 有限元模型验证

根据《应力强度因子手册》[18]，对于内壁含一条轴向半椭圆裂纹的管体，其裂纹前缘应力强度因子（KⅠ）可表示为：

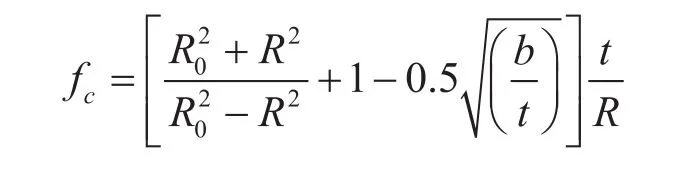
式中p表示管道内压，MPa；R表示管道内径，mm；t表示壁厚，mm；θ表示裂纹前缘某点与内壁夹角，（°）；c表示裂纹长半轴，mm；b表示裂纹短半轴，mm。

图3 三维输气管道有限元模型图

图4 管道裂纹前缘网格模型图

假设管道内壁有一轴向半椭圆裂纹，长半轴（c）为6.25 mm，短半轴（b）为5 mm，采用图4中的奇异单元法和3D-VCCT建立有限元模型，将所得模拟结果和《应力强度因子手册》计算结果对比，分析不同网格密度条件下两种数值模拟方法的精度差异。定义不同网格密度下数值模拟结果与理论结果的相对误差，可由下式得到：

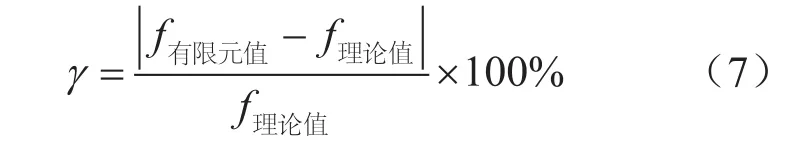
式中f有限元值表示3D-VCCT或奇异单元法数值模拟结果；f理论值表示《应力强度因子手册》计算结果。

从模拟结果和理论计算结果发现，半椭圆裂纹前缘各点的应力强度因子关于裂纹最深点对称，故仅分析裂纹前缘0°～90°各点应力强度因子的相对误差。图5为3D-VCCT法和奇异单元法在不同网格密度下的相对误差，A表示3D-VCCT裂纹前缘两侧各加密层，B表示奇异单元法裂纹前缘两侧各加密层。

图5 裂纹前缘不同角度下的相对误差图

对比奇异单元法与3D-VCCT法在不同角度下的相对误差值可知，3D-VCCT的计算精度明显高于奇异单元法，并且当裂纹前缘两侧各加密6层网格时3D-VCCT法的计算精度最佳，此时最大误差为1.45%。图6为裂纹前缘两侧各6层网格时3D-VCCT的Mises应力结果（图6-a、b）和奇异单元法的Mises应力结果（图6-c、d），从图6可以看出，两种方法都能真实反映裂纹前缘的应力集中现象。但进一步对比两种有限元模型的计算效率（表1）发现，3D-VCCT的计算效率较高。因此综合考虑裂纹面切分难易程度、有限元计算精度和计算效率，最终选择高精度、高效率的3D-VCCT方法、裂纹前缘加密6层网格作为后续多裂纹干涉效应分析的基础。

图6 3D-VCCT法与奇异单元法的Mises应力对比图

表1 3D-VCCT与奇异单元法的计算效率表

3.2 多裂纹干涉效应表征

为了定量表征附属裂纹对主裂纹的干涉效应，这里引入裂纹相互干涉作用因子（η），其表达式为：

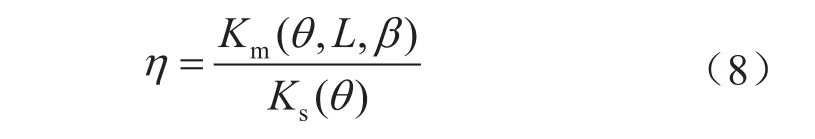
式中Km(θ, L, β)表示裂纹水平间距（L）和竖向间距（β）下主裂纹前缘在角度（θ）处的应力强度因子；Ks(θ)表示管道相同位置存在同尺寸单裂纹时裂纹前缘在角度（θ）处的应力强度因子。当η＞1时，表示附属裂纹的存在增大了主裂纹前缘的应力强度因子，具有增强效应；反之，当η＜1时，则表示附属裂纹对主裂纹具有减弱效应；当η=1时，表示附属裂纹的存在对主裂纹不产生影响；当∣η-1∣＜1%时，可认为附属裂纹对主裂纹的干涉效应忽略不计。

3.3 结果分析与讨论

3.3.1 裂纹形状对应力强度因子最大值点的影响

图7给出了长半轴（c）为6.25 mm，短半轴（b）为5 mm半椭圆裂纹前缘（0°～90°）各点的应力强度因子。从图7可以看出，应力强度因子在裂纹表面点和最深点存在极大值。为进一步探讨裂纹形状比对应力强度因子最大值点位置的影响，在图3-b有限元模型的基础上，保持裂纹短半轴（b）为5 mm不变，计算=0.50、0.77、0.78、0.80、1.00和 1.50情况下的值（ 表示裂纹表面点的应力强度因子，表示裂纹最深点的应力强度因子），其结果如图8所示。

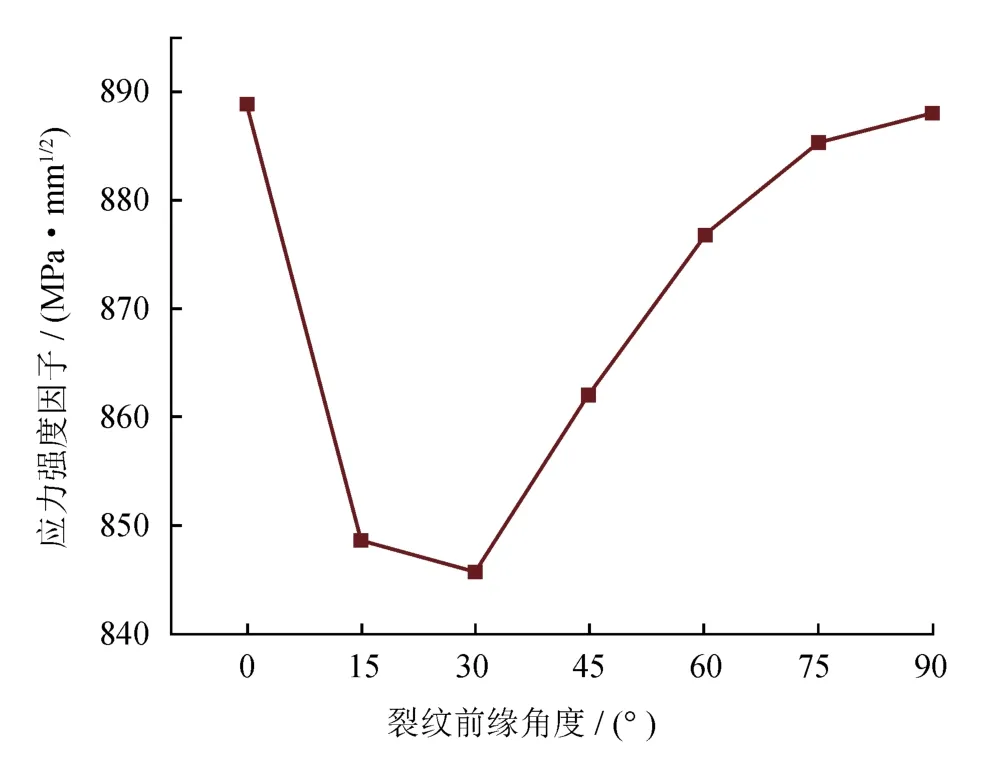
图7 裂纹前缘各点的应力强度因子图

图8 裂纹形状比对应力强度因子最大值点位置的影响图

3.3.2 裂纹尺寸对主裂纹的干涉效应

在获取裂纹形状比对应力强度因子最大值点位置的影响规律后，设定 ＜0.8并在此条件下建立3D-VCCT多裂纹干涉有限元模型，其中材料参数、载荷情况和边界条件均保持不变，输气管道多裂纹网格干涉模型如图9所示。

图9 输气管道多裂纹网格模型图

图10给出了当裂纹处于平行共线位置关系时附属裂纹尺寸变化对η的影响。由图10-a可看出，η随附属裂纹长度的增加而增加，而随主裂纹前缘各点角度的增加呈指数形式减小，当主裂纹前缘角度大于90°后，η值趋于稳定。由图10-b可看出，η随附属裂纹深度的增加而增加，而随主裂纹前缘角度的增大呈现先减少后略微增大的变化趋势，主裂纹最深点的增强效应最弱。综合图10-a、10-b发现，当附属裂纹存在时，主裂纹前缘各点的η均大于1，即主裂纹前缘各点受到了附属裂纹的增强效应，且近表面点的增强效应最明显，这是因为主裂纹近表面点与附属裂纹相距最近，应力叠加最严重（图11），故在对平行共线裂纹进行安全评定时需重点考虑近表面点。

图12分别给出了当裂纹处于平行共轴位置关系时，主裂纹前缘各点η随附属裂纹长度和深度的变化情况。由图12-a可看出，η在主裂纹最深点和表面点表现出不同的变化规律，即主裂纹最深点的η随附属裂纹长度的增加而增大，而主裂纹表面点的η却随附属裂纹长度的增加而减少。

图10 平行共线位置关系下附属裂纹尺寸变化对相互干涉作用因子的影响图

图11 平行共线位置关系下主裂纹与附属裂纹的应力干涉云图与单裂纹应力对比云图

图12 平行共轴位置关系下附属裂纹尺寸变化对相互干涉作用因子的影响图

由图12-b可知，当裂纹间的竖向间距较大时，附属裂纹对主裂纹前缘各点的∣η-1∣＜1%，裂纹间的干涉影响可忽略不计；但随着附属裂纹深度的增加，裂纹竖向间距不断减小，主裂纹表面点开始产生减弱效应，且减弱效应随附属裂纹深度的增加而增强；值得注意的是，当b2/t≥0.3时，主裂纹最深点开始产生明显的增强效应。从图12-a和图12-b不难发现，对于平行共轴裂纹，裂纹之间的相互干涉产生增强效应或者减弱效应，当裂纹竖向间距小于一定数值后主裂纹表面点产生减弱效应，而最深点产生增强效应，并且干涉效应随附属裂纹深度或长度的增加而增强。图13为平行共轴位置关系下主裂纹与附属裂纹相互干涉的Mises应力云图与单裂纹应力云图的对比，从图13可以看出，由于双裂纹的相互干涉效应，主裂纹表面点的应力明显降低，而最深点的Mises应力在增大，因此在进行安全评定时需重点考虑裂纹最深点。

3.3.3 裂纹间距变化对主裂纹的干涉影响

为揭示裂纹间距对相互干涉作用因子的影响，保持主裂纹和附属裂纹尺寸不变，通过变化裂纹水平间距（L）来开展多裂纹相互干涉效应研究，其结果如图14所示。

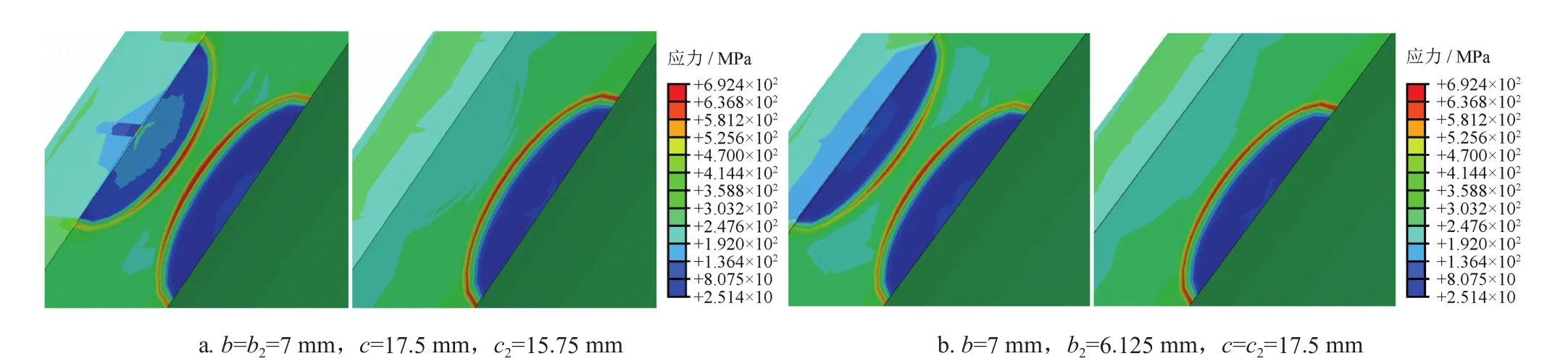
图13 平行共轴位置关系下主裂纹与附属裂纹的应力干涉云图与单裂纹应力对比云图

图14 裂纹距离变化对主裂纹相互干涉作用因子的影响图

从图14-a可知，当裂纹处于平行共线位置关系时，主裂纹前缘各点的η随着水平间距L1的增大而逐渐减少并趋近于1，说明随着裂纹水平间距的增大，裂纹前缘的应力逐渐得到释放，从而导致主裂纹受附属裂纹的增强效应愈来愈弱。

从图14-b可以看出，当裂纹处于平行偏置位置关系时，随水平间距的增大，主裂纹前缘各点的η逐渐增大并趋近于1，这是因为随裂纹间距的增大，主裂纹与附属裂纹相互远离，应力屏蔽效应减弱。综合图14-a和图14-b发现，当裂纹水平间距L≥6c时，主裂纹前缘各点的∣η-1∣＜1%，此时在对多裂纹进行安全评定时可不考虑附属裂纹对主裂纹的干涉影响。

4 结论

1）单一半椭圆裂纹应力强度因子（K）的最大值点与裂纹形状比有关，随着的增加，的值逐渐增大，而当＜0.8时，K的最大值点由裂纹表面点转移至裂纹最深点。

2）对于平行共线裂纹而言，附属裂纹的存在将使主裂纹前缘各点产生增强效应，且随附属裂纹深度或长度的变化，主裂纹近表面点的增强效应最为显著。

3）对于平行共轴裂纹而言，附属裂纹的存在不仅存在增强效应也存在减弱效应，当裂纹竖向间距较小时，主裂纹表面点表现为减弱效应而最深点表现为增强效应，且干涉效应随附属裂纹深度或长度的增加而增强。

4）当裂纹间的水平间距大于主裂纹长半轴的6倍时，平行共线裂纹与平行偏置裂纹的干涉效应微乎其微，此时在对多裂纹输气管道进行安全评定时可不考虑裂纹间的相互影响，直接将多裂纹简化为单裂纹处理。