输油泵出口管线流固耦合振动分析及减振措施
赵学俭
中国石化胜利油田分公司油气集输总厂, 山东 东营 257100
0 前言
随着国家经济建设的快速发展,石油产品已被广泛应用到国民经济的各个方面,尤其在交通运输、军事、工业燃料等领域发挥着巨大的作用。管道运输作为石油输送的主要方式,承担着重要的原油运输任务。而输油泵管线是油田输油生产的关键设备之一,其能否正常运行,直接关系到整个输油装置的运转[1-2]。因此,研究输油泵管道的振动特性,减少设备运行中事故发生的可能性,提高输油泵管线的安全性和经济性具有重要的理论和现实意义。
国内外学者对充液管道的振动问题进行了坚持不懈的研究,主要包括:1)线性流固耦合管道振动分析,以经典的水锤理论为代表,将管道的弹性引入压力波的船舶速度中,管壁的惯性和轴向运动没有考虑,只适合于全管刚性固定的管道[3-7];2)非线性流固耦合管道振动机理的研究,包括管道横向挠度引起的轴向拉力对其动力学特性的影响,定常流和振荡流作用下悬臂管的分岔与混沌行为,支撑输流管的振动稳定性以及振荡流导致的参数共振等,由于非线性问题的复杂性,一些非线性振动机理问题还亟待解决[8-14];3)管道系统的振动实验方法研究,包括管道系统的压力谱无扰测量、管道系统的能量流测定等,主要为了验证管道流固耦合动力学模型的正确性[15-18];4)管道系统动强度设计研究,主要包括波涌、温度等因素导致管壁材料塑性和勃性变形,材料的缺陷、液体腐蚀、管道振动疲劳直接影响管道动态寿命,随着非弹性材料输流管的广泛应用,这些问题愈来愈受到重视[19-22]。
在相关研究中,国内外学者结合不同的研究目的,开展了大量有关输液管道振动特性方面的研究,在理论和实验方面均取得了一定的成果,但由于流固耦合问题的复杂性,流固耦合方程的建立还存在许多假设,远远没有达到解决实际工程问题的需要,具有复杂边界条件的实际工程问题,很难给出解析解,需要采用数值计算方法进行反复迭代计算才能得到分析结果。在工程问题上可以采用数值模拟方法对流固耦合过程进行求解。本文基于ANSYS对输油泵出口管线进行了数值仿真计算,得到了不同支撑情况下管线的固有频率、应力和应变情况,得到了流体与管道相互影响下管道的振动频率,根据数值计算结果和现场测试结果提出了相应的减振方案。
1 模态分析
采用SOLIDWORKS软件建立管路的三维模型,导入ANSYS软件利用SOLID 95单元对模型划分网格,输油泵出口管路模型,见图1。
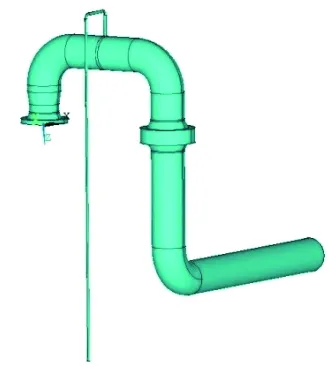
a)几何模型

b)网格模型
对管路进行有预应力的模态分析能够更好地模拟实际情形,提高分析的可靠度,因此对管路进行模态分析时,需考虑重力在内的预应力影响。根据现场工况,管路的约束主要是在管路端面和部分管路施加全约束,进行模态分析得到其前10阶固有频率,见表1。输油泵出口管路部分振型图,见图2。
通过对管路结构进行模态分析,可以确定系统的固有频率,通过设计和优化,避开共振区,防止管路发生共振被破坏。通过表1和图2可知,管路上的回油放气管较细,其刚度最小,振动幅度最大。第3阶、第5阶、第7阶模态为主管路振动模态,主要为管路无支撑所致。
表1 输油泵出口管路的前10阶固有频率

阶次12345678910频率/ Hz7.258.3816.5719.1522.7023.2128.0932.1644.3950.55
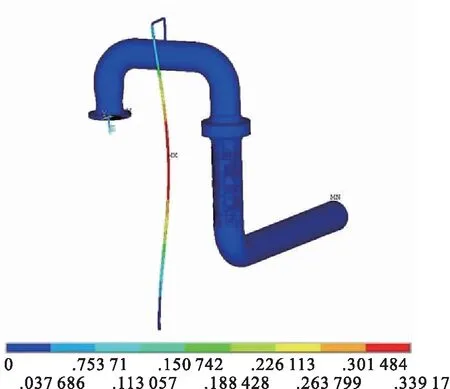
a)1阶振型
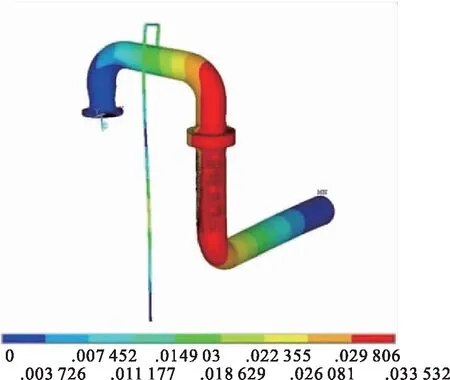
b)3阶振型
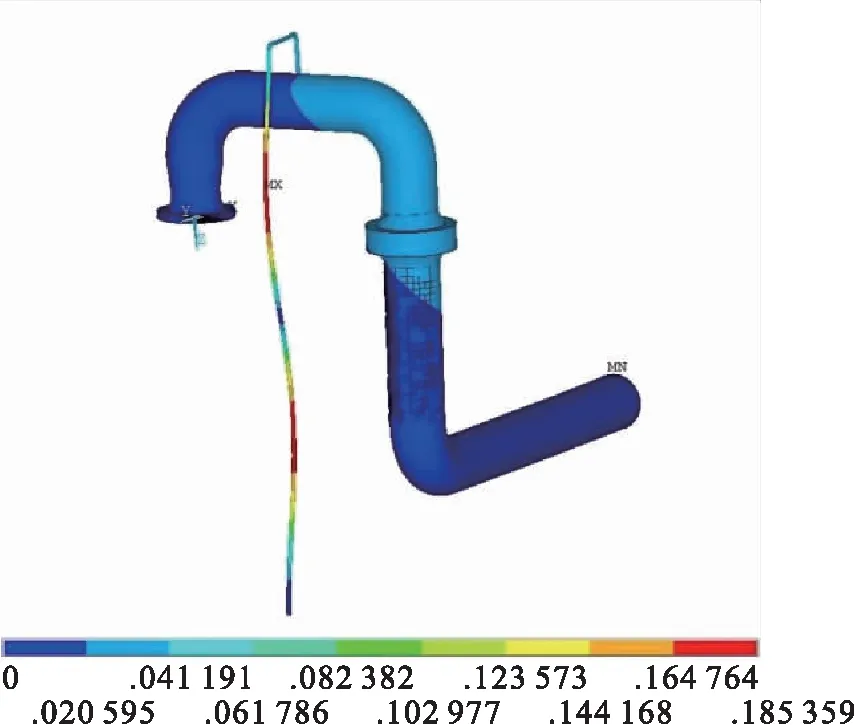
c)5阶振型
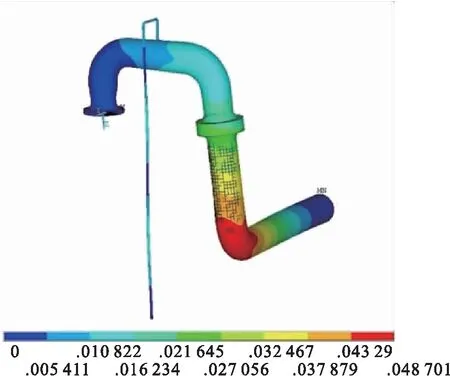
d)7阶振型
2 热-应力耦合分析
本文采用间接耦合分析方法,首先对管道进行稳态热分析,在管道内侧施加50 ℃的温度,在管道外侧施加20 ℃的温度,得到管道各部分的温度分布情况,见图3。
在管道内侧分别施加3.8 MPa和5 MPa内压,对管道进行热-应力耦合分析,得到位移和应力云图,见图4~5。
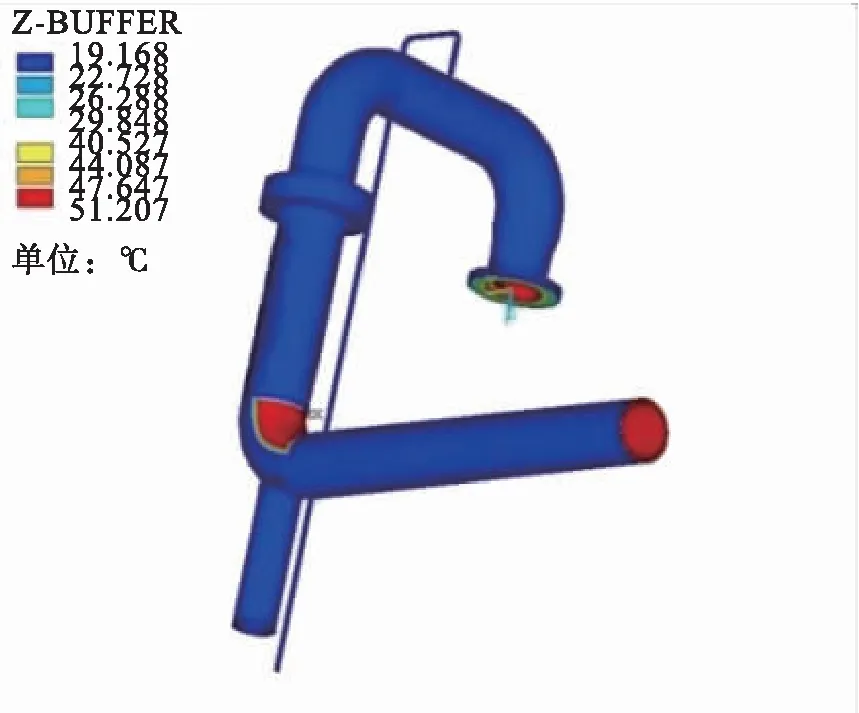
a)整体模型
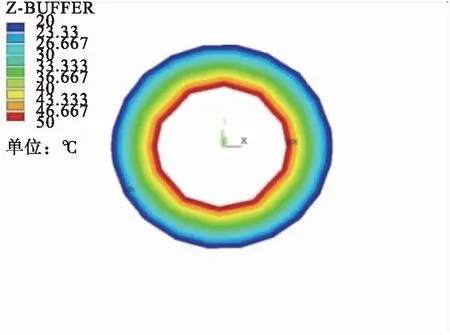
b)管道截面
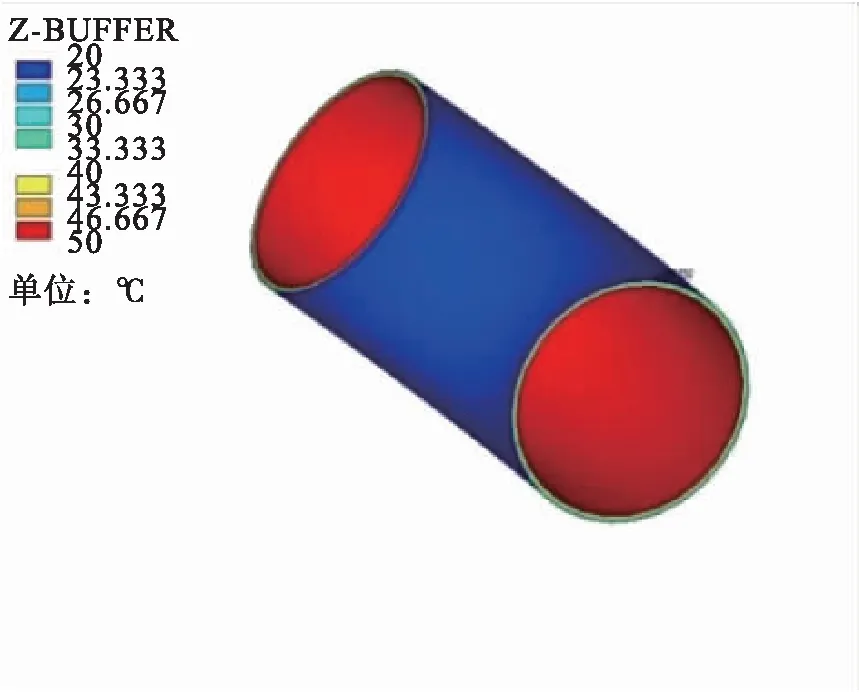
c)弯管部分
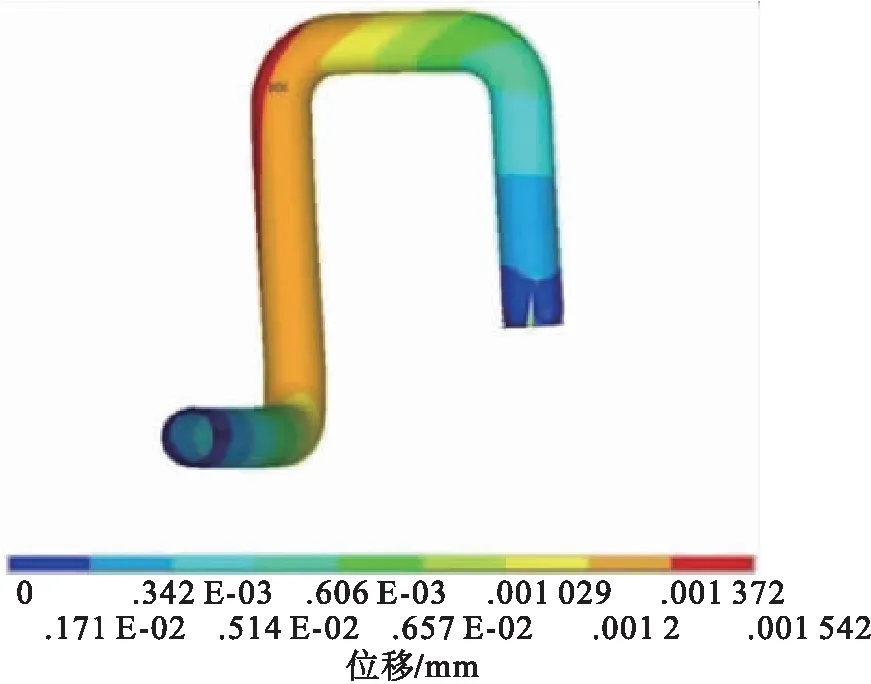
a)内压3.8 MPa
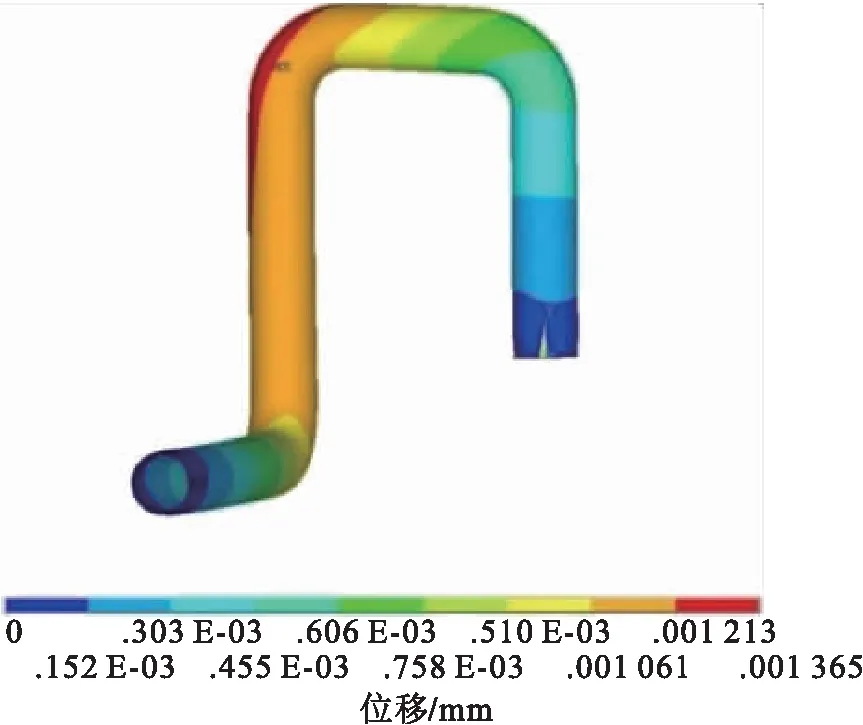
b)内压5 MPa
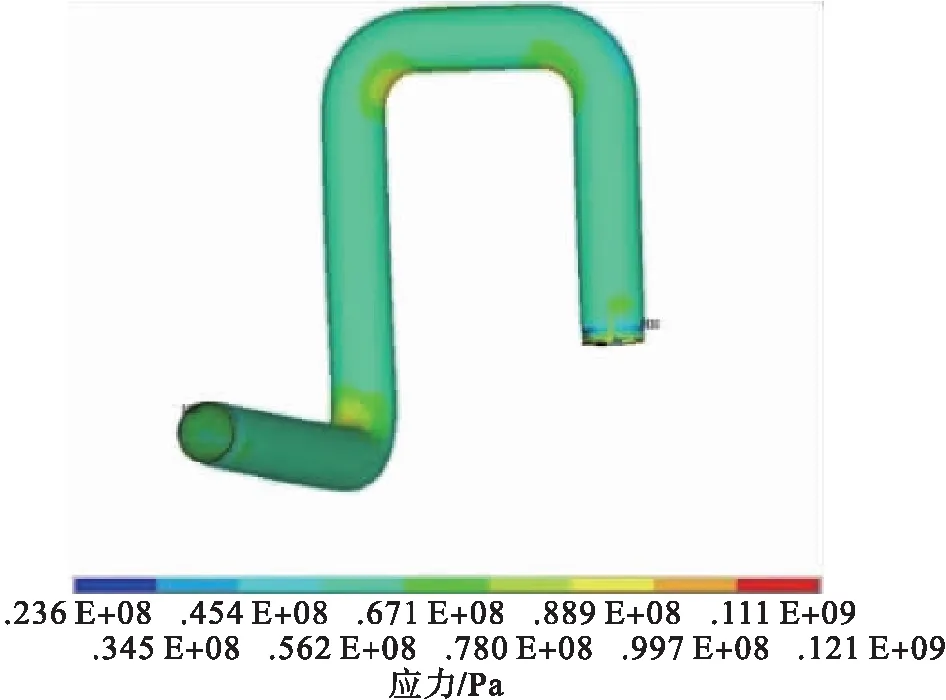
a)内压3.8 MPa
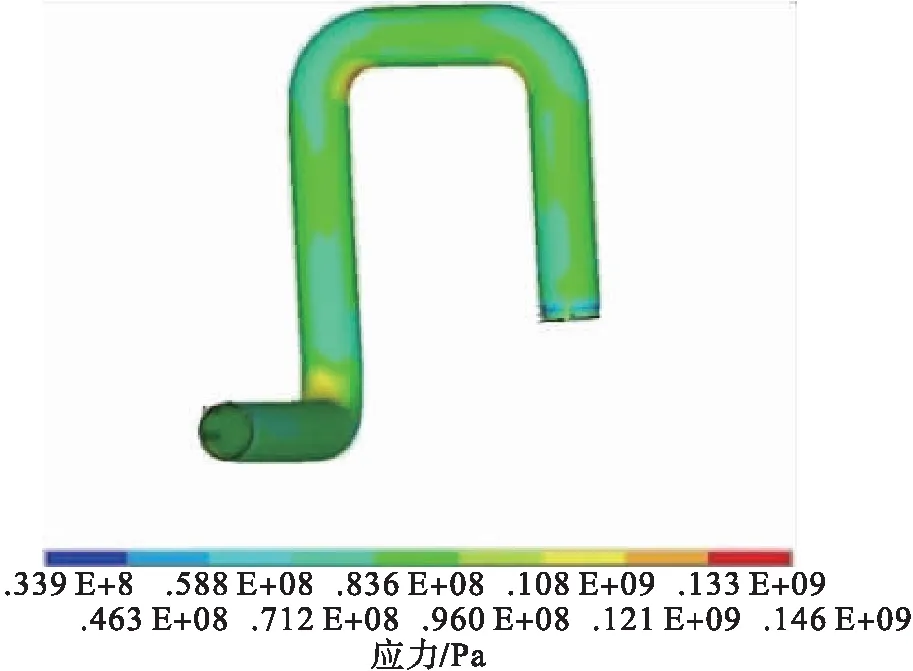
b)内压5 MPa
由图4~5可知,管道最大变形发生在管道上部的弯头处,3.8 MPa内压下为13.7 mm,5 MPa内压下为15.4 mm;最大应力发生下部的管道弯头处,3.8 MPa内压下为121 MPa,5 MPa内压下为146 MPa,管道弯头处应增加支撑。
3 流固耦合分析
输液管道结构的耦合作用一般可分为流固耦合、波流耦合和波波耦合三类。在分析研究波流耦合和波波耦合时需要考虑流体的压缩性,而一般研究时都忽略流体的压缩性,所以对后两种耦合的研究很少,而对流固耦合的研究较多,本文采用流固耦合方法对输油泵出口管线进行耦合分析。
基于ANSYS Workbench平台,分别建立流体网格和固体网格,见图6。入口压力3.8 MPa,流量131.26 kg/s,流体为原油,密度945.1 kg/m3,黏度0.301 4 kg/(m·s)。
为了准确找到流体对管道作用力的频率,选取了多个时段和时间点进行双向流固耦合计算。根据情况分别计算2个支撑和3个支撑条件下,管道所受流体作用压力。

a)流体网格

b)固体网格
3.1 40 s时双向流固耦合计算
管道采用3个固定支撑,1个为泵出口管道端面,1个为下游阀支点,1个为图7中所指的环形截面。
设置非稳态计算步长为0.5 s,总时间步为80步,共计0.5 s×80步=40 s,计算结果见图8。由图8可知,管道最大总变形量为0.383 mm,出现在图8红色位置,最大主应力为144 MPa,最大应力系数为0.53。

图7 约束加载

a)总变形量

b)最大主应力

c)应力系数
各方向管道受力随时间变化情况见图9~11,1个周期大约2 s(频率f约0.5 Hz),远低于实测管道振动频率。
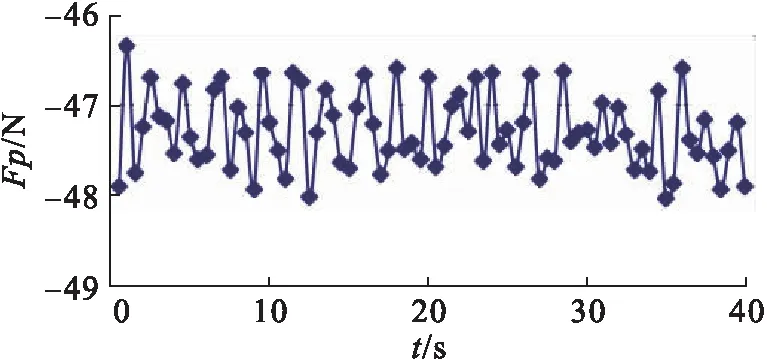
图9 X方向管道所受流体压力
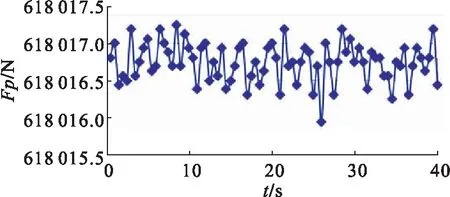
图10 Y方向管道所受流体压力

图11 Z方向管道所受流体压力
3.2 单元流固耦合计算
建立多个流固计算单元串联进行计算,首先计算0.000 1 s/步×10步=0.001 s,然后计算0.001 s+0.000 1×9步=0.01 s,0.01 s+0.000 1×100步=0.02 s,0.02 s+0.001×40步=0.06 s,0.06+10-5×10步=0.060 1 s,直至0.060 1 s+0.000 15 s=0.060 25 s。计算得开始计算段周期T=0.21 s,f=4.76 Hz;继续计算管道受力,得振动频率f=6.58 Hz。两个时段管道应力变化见图12。
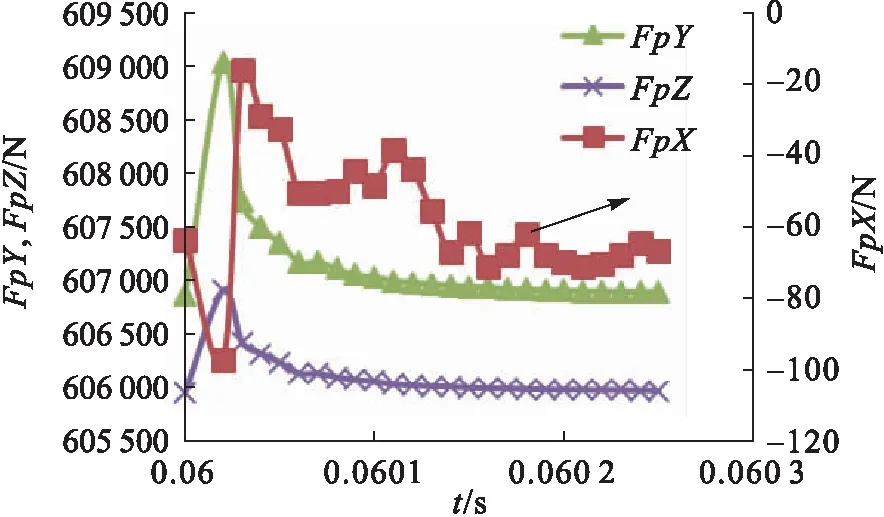
a)前期
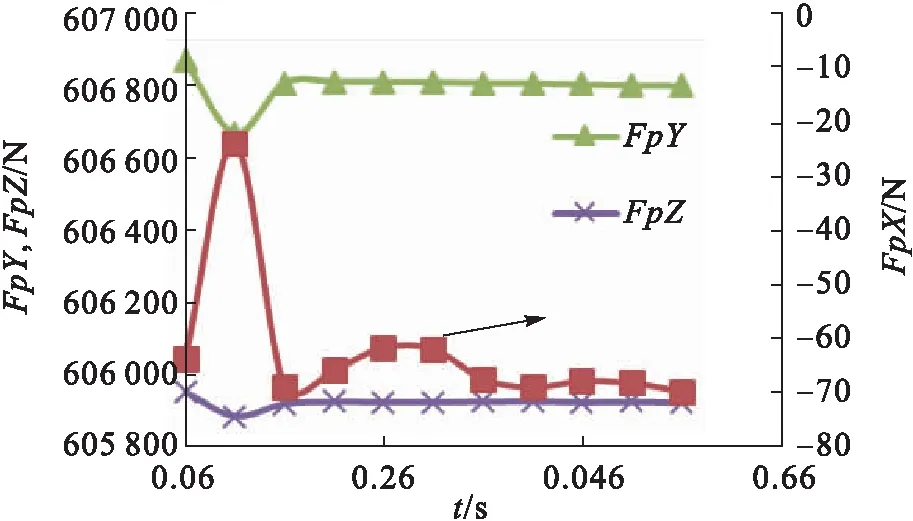
b)后期
通过对出口管道进行流固耦合分析,在较短时间(0.05 s)内,引起的管道振动频率约7 Hz,随着时间的推移,应力开始趋于稳定,40 s时管道振动频率为0.5 Hz。由原油流动引起的管道振动频率与管道的第1、2固有频率相当,都为7 Hz左右,可能引起管道的共振。
4 减振方案设计
4.1 单阻尼器减振方案
将管道阻尼器安装在管道弯头处下面的正下方见图13。

图13 阻尼器安装示意图
图14分别是阻尼器安装前后输油泵的振动波形图,测试安装阻尼器前后管道的振动情况。
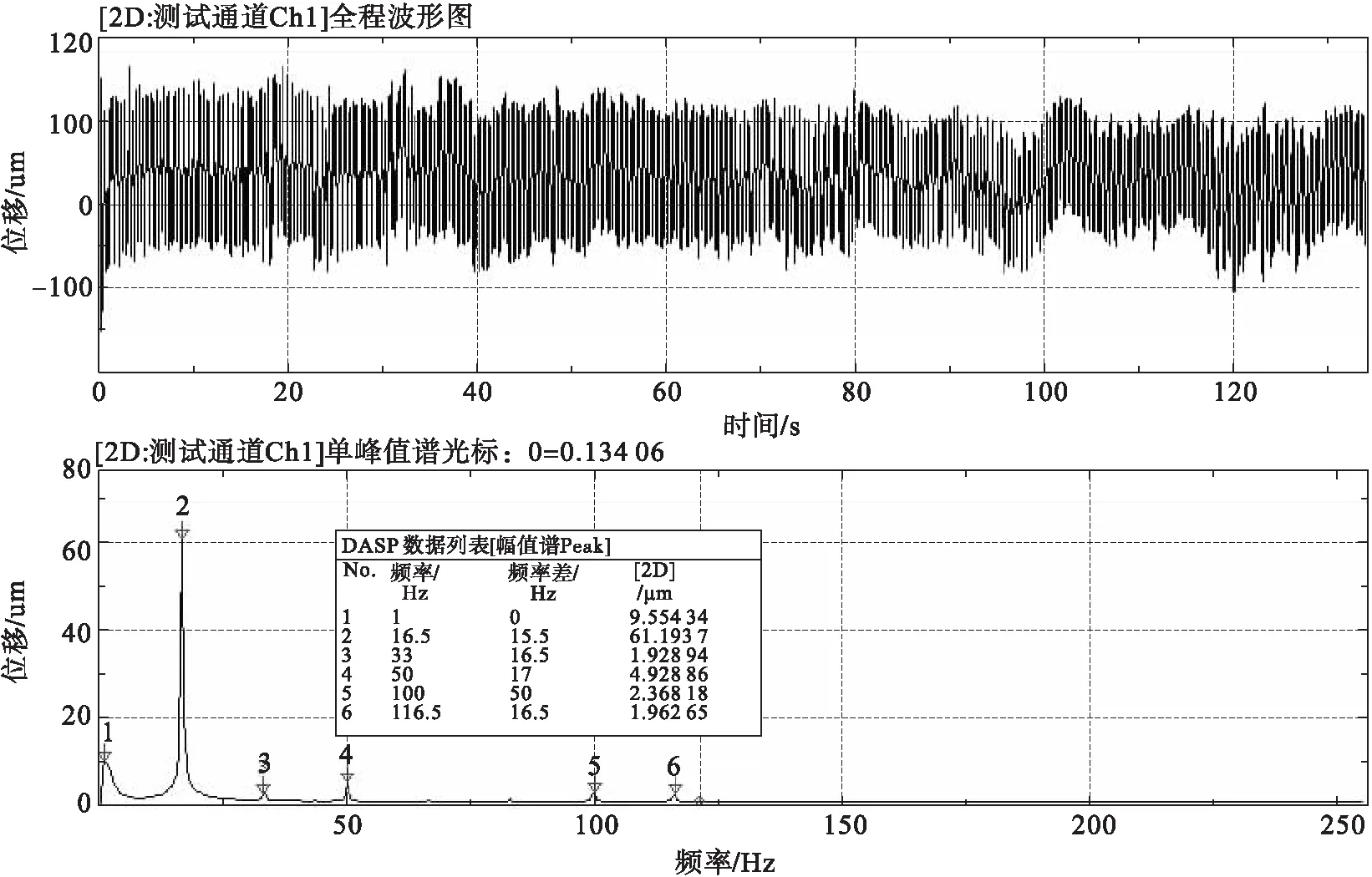
a)未安装阻尼器
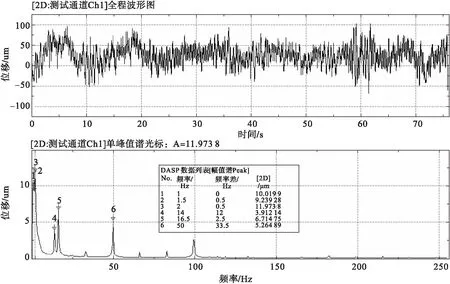
b)安装阻尼器
由图14可知,安装阻尼器前3号螺杆泵的振动幅值主要在-0.8~+0.12 mm之间,安装阻尼器后3号螺杆泵的振动幅值主要在-0.05~+0.07 mm之间,与安装阻尼器前,管道振动幅值有一定程度衰减,由此可以看出管道阻尼器对管道振动有一定的衰减作用。
4.2 双阻尼器减振方案
双阻尼器见图15。将2个阻尼器对称布置,以避免由于偏心布置引起的弯矩;同时,管道阻尼器必须保持垂直,以避免阻尼液外流到壳体中;安装时,为了确保将阻尼器安装在管道振动最强烈的位置,应先检测管道的振动情况,然后根据管道振动最强烈的位置调整管柱长度,使阻尼器安装在管道振动最强烈的位置。

图15 双阻尼器安装示意图
5 结论
1)基于ANSYS软件建立了输油泵出口管线的有限元模型并进行了模态分析,得到了管线前10阶固有频率和振型,为后期优化设计提供了理论支撑。
2)通过对输油泵出口管线的热-应力耦合分析可知,管道最大变形发生在管道上部的弯头处,3.8 MPa内压下为13.7 mm,5 MPa内压下为15.4 mm;最大应力发生下部的管道弯头处,3.8 MPa内压下为121 MPa,5 MPa内压下为146 MPa,管道弯头处应增加支撑,管道弯头处应增加支撑。
3)通过对输油泵出口管道进行流固耦合分析可知,在较短时间(0.05 s)内,引起的管道振动频率约7 Hz,随着时间的推移,应力开始趋于稳定,40 s时管道的振动频率为0.5 Hz。
4)在管道弯头处,管道的振动和位移较大,应在管道的弯头处增加支撑,根据设计方案安装单阻尼器和双阻尼器。

