胶合木T梁弯曲承载力试验研究

杨 涛，王解军，宁 凡，饶真宇

（中南林业科技大学 土木工程学院，湖南 长沙 410004）

欧美学者提出一种由实木锯材正交叠放组胚、结构胶粘结制作的工程绿色建筑材料CLT（Cross laminated timber）正交板，具有良好的整体力学性能和双向强度、自重轻等优点，被广泛应用于欧洲桥面结构[1-2]。至今，关于胶合木矩形梁及正交板（CLT）的弯剪性能已有较多研究[3-8]，并取得了大量成果。Rammer[9]通过试验与理论研究，提出了胶合木矩形梁的剪切强度计算公式。

为了增强结构整体性，减小结构振动与变形，减小截面尺寸，节省材料，降低造价，采用桥面板与肋梁胶合，避免钉合产生应力集中、锈蚀松动等缺点[10]，提高结构耐久性，考虑到桥面板主要横向受弯的特点与木材力学特性，本研究提出一种理论上适合工程应用的正交胶合木T 梁，且以兴安落叶松为原材，采用新型水基聚氨酯胶粘剂胶合，研究其弯曲承载力，同时与平行胶合木T梁、矩形梁对比试验，分析应变、挠度及极限承载力，探讨各类构件的破坏形态和破坏机理，探究正交T 梁的弯剪承载力计算公式。以往研究常局限于胶合木矩形梁，阻碍了木结构件发展，通过研究木层板排列方向和截面形式对胶合木梁的受力影响，为今后胶合木构件设计提供理论依据。

1 材料与方法

1.1 构件材料及设计

制备3 组共6 根胶合木梁，兴安落叶松物理力学性能由材性实验测得，聚氨酯结构胶物理力学性能由南京天竹科技实业有限公司提供（表1）。A 组（2 根）：平行胶合木T 梁，翼缘板与肋梁的木材顺纹方向相同。B 组（2 根）：正交胶合木T梁，翼缘板与肋梁的木材顺纹方向垂直。C 组（2根）：胶合木矩形梁（用于对比）。正交与平行T梁尺寸相同，均为250 cm×25 cm×29 cm（长×宽×高），两者高跨比均为1/7.6。T 梁截面由肋板和翼缘板组成，梁顶部胶结250 cm×25 cm×5 cm（长×宽×高）的翼缘板；矩形梁与T 梁的肋板尺寸相同，为250 cm×7.5 cm×24 cm（长×宽×高），高跨比为1/9.2。所有胶合木梁均满足《木结构设计规范》[11]构造要求。

1.2 试验方法

试验装置如图1所示，梁计算跨径I0为2.2 m，采用三分点加载[12]，T 梁剪跨比为2.52，矩形梁剪跨比为3.04，均小于6（剪跨比小）。采用三脚架固定肋板两侧以防止侧向失稳，在地基支座、分配梁支座以及跨中共设置5 个百分表，分配梁顶部设置20 t 压力传感器；在T 梁跨中翼板顶部均匀布置5 片应变片，肋板顶部（与翼板交接处）、中部、底部对称布置2 片应变片，在T 梁中性轴肋梁一侧布置1 片应变片，共12 个应变测点；矩形梁则在跨中截面左右对称且均匀分布5 片应变片，共10 个应变测点。试验加载主要测试3 组构件挠度、极限荷载和跨中截面应变。采用分级加载方式，所有测量数据均由TST3826 静态应变测试系统同步采集。

2 结果与分析

2.1 破坏形态与机理

实验中三类胶合木梁工作情况类似，代表性破坏形态见图2a ～c，梁局部剪切裂缝见图2d ～e。初始时梁处于弹性工作阶段，当荷载增大至极限荷载的75%～90%时，木梁发出清脆声响，在梁肋中部加载位置附近出现可见的细微初始裂缝；随着荷载继续增大，木梁产生低沉密集声响，初始裂缝逐渐扩展趋向贯通，木梁表面出现褶皱或微裂缝（垫板木材受压屈服凹陷褶皱或木材材料缺陷产生的细微裂缝见图2f），梁严重挠曲；达到极限破坏荷载时，伴随突然的巨响，肋梁中部附近出现较长的贯通纵向裂缝，之后迅速向梁两端扩展，木梁弯曲破坏。

表1 材料物理力学性能Table1 Physical and mechanical properties of the materials

图1 试验加载与测点布置（尺寸单位：cm）Fig.1 Test loading and strain measuring point arrangement (unit: cm)

图2 胶合木梁破坏形态Fig.2 Failure modes of glued timber beams

三类胶合木梁的破坏形态均属于典型的顺纹剪切破坏。由于木材顺纹方向的抗拉压强度较高，抗剪强度低，而本次试验胶合木梁的高跨比大（T梁高跨比为1/7.6、矩形梁为1/9.2，均大于1/10，远大于1/18）、剪跨比小（T 梁剪跨比为2.5、矩形梁剪跨比为3.0，均小于6），其抗弯能力强于抗剪。木材顺纹方向抗剪强度最弱，两个加载位置（荷载作用点）梁截面中性轴附近剪应力最大，当其超过木材顺纹剪切极限强度时，即发生剪切破坏，产生初始裂缝；继续加载使得初始裂缝向跨中延伸为贯通裂缝，这条贯通的水平裂缝即为胶合木梁的剪切主裂缝；随着荷载继续增大，主裂缝延伸至梁端，胶合木梁破坏。平行T 梁、正交T 梁及矩形梁的剪切主裂缝均位于截面中心轴下侧（受拉侧），距中性轴1 ～5 cm，典型的剪切主裂缝分布如图2g 所示。剪切主裂缝位于截面中心轴下侧，是由于梁受弯时，梁顶木材受压屈服早于梁底木材受拉屈服，导致梁截面中心轴逐步下移，最大剪应力位置也随着下移，即最大剪应力发生在截面初始中心轴的下侧附近。

胶合木梁的其它区域产生较轻微的随机裂缝，是由于木材缺陷或胶合面脱胶导致的，但对结构整体受力影响较小。胶合木梁顶、底面尚未压、拉破坏，即使翼缘板是横纹的正交T 梁，也是肋板顺纹剪切破坏。

2.2 荷载-挠度曲线

各构件的荷载-挠度曲线及力学性能数据分别见图3和表2。

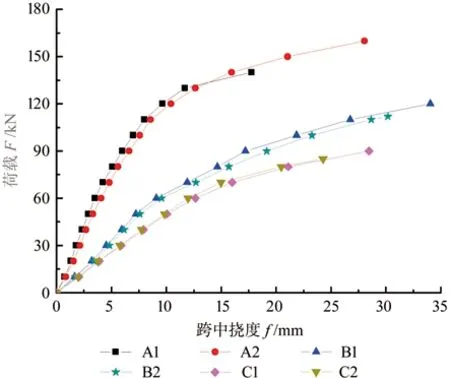
图3 荷载-跨中挠度曲线Fig.3 Load - midspan deflection curves

表2 构件力学性能试验数据Table2 Mechanical properties test data of the components

由图3可知，A 组构件（平行T 梁）的承载力大于B 组构件（正交T 梁），矩形梁的承载力最小。本文基于Bazan[13]提出的木材双线性拉压本构关系，木材受拉几乎无屈服阶段，把受压区开始进入塑性阶段定义为屈服点。对3 类胶合木T 梁构件的结构力学性能（平均值）进行比较，结果见表2。由表2可知，正交T 梁与矩形梁相比，其极限承载力提高了33%，抗弯刚度提高了28%，延性系数提高了25%；平行T 梁与正交T梁相比，其极限承载力提高了30%，抗弯刚度提高了117%，延性系数基本相同。正交T 梁的翼缘板虽然是横纹，但相比矩形梁（无翼缘板），其承载力、刚度和延性系数均有较大的提升。

2.3 荷载-竖向应变曲线

胶合木T 梁和矩形梁跨中截面沿竖向高度均布置5 个应变测点（图1），从上至下进行编号1、2、3、4、5，竖向应变大小均为同一高度所测应变数据的平均值，荷载-竖向应变曲线见图4。其中：负号表示受压，正号为受拉。

由图4可知，胶合木梁弹性阶段荷载-应变曲线满足线性分布，基本符合平截面假定；当进入塑性阶段，木材纤维压应力的增长逐渐减小，而受拉侧应力、应变仍为线性关系，截面中性轴逐渐下移，木梁受压面积增大，木材抗压屈服点明显小于抗拉屈服点。

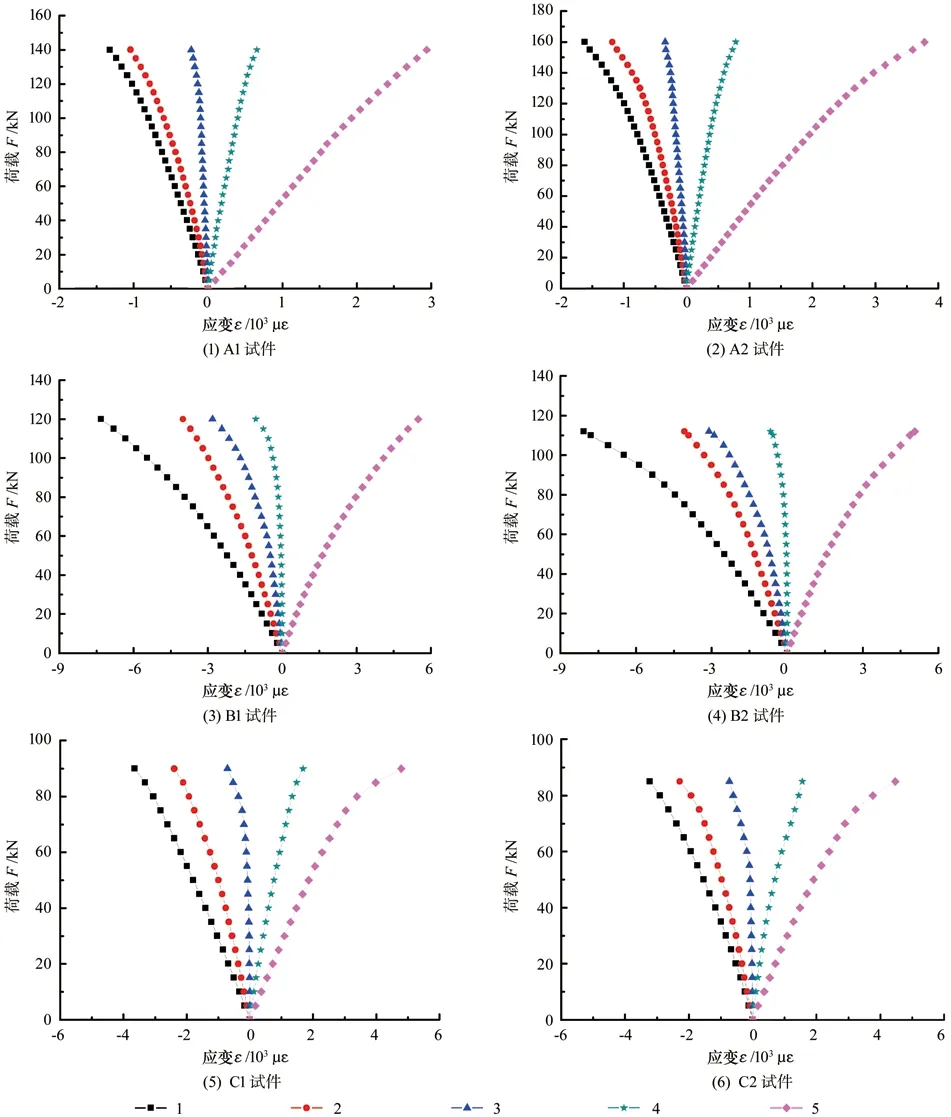
图4 荷载-应变曲线Fig.4 Load-strain curves

平行T 梁3 号、正交T 梁4 号和矩形梁3 号应变测点，弹性阶段应变变化很小，与理论计算中性轴相符；T 梁翼缘板与肋板之间无相对滑移、应变协调，两者交接处粘结安全可靠。

2.4 T 梁翼板应变的横向分布

胶合木T 梁跨中截面翼板顶部沿横向均匀布置5 个纵向应变测点（图2），各级荷载下，翼板纵向应变的横向分布曲线如图5所示。

由图5可知，正交、平行T 梁翼板的正应力（纵向应力）在横向呈不均匀分布，中间大、两端小，即存在剪力滞现象。极限荷载下，平行T 梁翼板的应力横向分布类似三角形，变化激剧，中间的应变峰值比两端应变大38%（平均）；而正交T梁翼板正应力的横向分布类似抛物线，变化平缓，中间的应变峰值比两端应变大26%（平均）。两者翼板弯曲弹性模量不同，导致应变差异，横纹弯曲弹性模量一般为顺纹弹性模量的1/10[14]，因此正交T 梁翼板各点应变均大于平行T 梁。

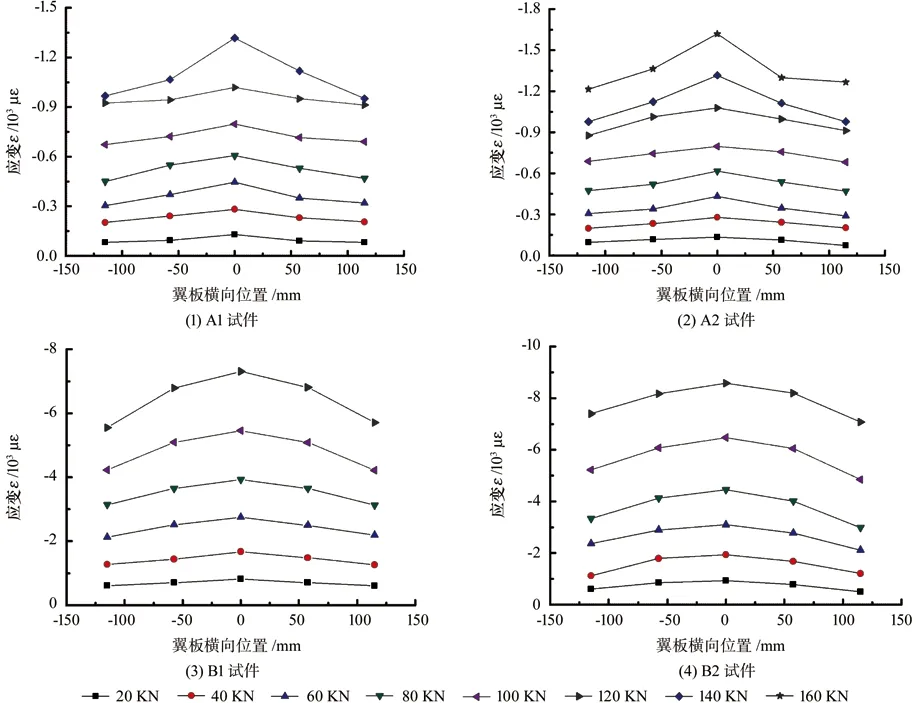
图5 T 梁跨中截面翼板应变的横向分布曲线Fig.5 Transverse distribution curves of beam flange plate in T-beam mid-span section

2.5 极限承载能力分析

本次试验的胶合木T 梁剪跨比为2.52，矩形梁剪跨比为3.04，均小于6。由于剪跨比较小，胶合木梁受弯时，均发生顺纹剪切破坏，此时木梁的抗弯承载力可由其抗剪强度来确定[15]。

假设木材均匀，层板间粘结完好，无相对滑移，梁达到开裂荷载时视为已发生剪切破坏，由荷载-应变曲线（图4）可知，塑性阶段木梁截面中性轴移动较小，忽略中性轴移动对胶合木梁剪切性能的影响。T 形梁腹板和矩形梁截面的剪应力τ（图6）可按式（1）求得：

式中：Fz为横截面上的剪力，其Pc/2；Sz为截面距中性轴y横线以外部分的面积对中性轴的静矩；Iz为整个截面对其中性轴的惯性矩；d1为T 梁腹板厚度或矩形梁宽度。

由剪应力互等定理可知，微元体竖向剪应力τ与水平向（顺纹）剪应力τ′相等。T 梁和矩形梁截面最大剪应力τmax均发生在中性轴（与梁底距离为）位置，当中性轴处顺纹最大剪应力τ′max达到极限强度时，梁即剪切开裂。

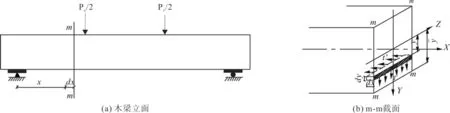
图6 木梁截面剪应力计算示意图Fig.6 Schematic diagram of shear stress calculation for wood beam section

对于正交胶合木T 梁，因翼板与肋板截面的材料弹性模量不同，按刚度等效原则，将其等效为平行梁（图7）。考虑截面高度不变，等效后翼板的宽度由式（2）计算：

式中：d2、d3分别为正交梁和等效平行梁的翼板宽度，本文等效平行梁翼板宽度为25 mm；E1、E2分别为木材顺纹和横纹方向的抗弯弹性模量。

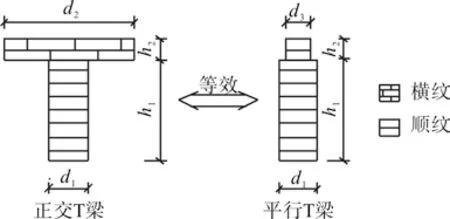
图7 正交梁等效为平行梁Fig.7 Cross glulam beam equivalent to parallel glulam beam

胶合木梁的剪切强度与其它材料一样存在尺寸效应，随着截面积或体积的增大而逐渐减小[16]。Rammer[9]提出了胶合木矩形梁的剪切强度计算公式：

式中：τb为胶合木梁的剪切强度；Kf为调整木材实际破坏强度的应力集中因子，取值 2；τm为木材顺纹剪切强度，落叶松木材顺纹剪切强度取9.0 Mpa[17]；A为木梁的有效剪切面积，可按材料力学有关公式计算。

根据各组试件开裂荷载Pc 的平均值，按式（1）求得其截面中心轴顺纹最大剪应力τ′max（正交梁等效为平行梁计算），即极限弯曲剪应力试验值；并按Rammer 公式（3）计算梁的抗剪强度τb（理论值），结果见表3。由表3可知，T 梁（A 组和B组）的极限剪应力试验值比抗剪强度理论值略大，相差分别为2.6%、1.4%；矩形梁（C 组）的极限剪应力试验值与理论值相比，相差-5.9%，符合较好。表明Rammer 矩形梁的抗剪强度公式不仅适合于矩形梁，同时也适合于正交与平行T 梁的抗剪强度计算。

表3 胶合木梁极限弯曲剪应力试验值与理论值比较Table3 Comparison of theoretical and experimental values of ultimate bending shear stress for glued timber beams

3 结论与讨论

3.1 结 论

通过落叶松胶合木正交T 梁、平行T 梁及矩形梁共3 组（每组2 根、共6 根）试件的抗弯承载力试验，可得到以下结论：

1）当胶合木梁的高跨比较大（大于1/10）、剪跨比较小（不大于3）时，受弯时均为中部顺纹通缝剪切破坏，破坏前梁腹部均出现褶皱、裂纹及声响，属脆性破坏。正交T 梁与矩形梁相比，其极限承载力提高了33%，抗弯刚度提高了28%，延性系数提高了25%；平行T 梁与正交T梁相比，其极限承载力提高了30%，抗弯刚度提高了117%，延性系数基本相同。正交T 梁的翼缘板虽然是横纹，但相比矩形梁（无翼缘板），其承载力、刚度及延性均有较大的提升。

2）胶合木梁受拉侧荷载-应变曲线表现为线弹性，而受压侧表现为弹塑性，其截面应变沿梁高基本呈线性，符合平截面假定。当木梁进入塑性阶段后，中性轴缓慢向受拉侧移动，中性轴弯曲剪应力最大，剪切破坏通缝发生在靠初始中性轴受拉侧附近。

3）关于胶合木T 梁抗弯承载力计算方法，本文基于刚度等效原则，提出了将正交T 梁等效为平行梁，然后采用Rammer 公式来计算其弯曲剪切强度的策略，扩展了Rammer 公式的适用范围。试验与理论计算结果比较表明，两者较符合，所提出的策略合理、可靠。

4）正交T 梁翼板正应力横向分布曲线显得平缓，呈抛物线变化；平行T 梁翼板正应力横向分布曲线变化较激剧，腹板处峰值突出。

3.2 讨 论

本文针对胶合木廊桥中的T 梁抗弯承载力开展了试验研究，揭示了T 梁受弯主要为顺纹剪切破坏的特征（规律）。T 梁翼板与肋板之间的结合面不存在脱胶、开裂现象，并且T 梁（含正交与平行梁）的弯剪强度均大于矩形梁，得到了量化结果，同时提出了T梁抗弯承载力的理论计算方法。这些成果具有理论与工程应用意义，也是本文的创新点。需要进一步研究的问题如下：

1）宜增加试件个数（包括各种不同尺寸的试件），继续开展试验研究，以提高试验统计结果及结论的可靠性。

2）应考虑剪力滞效应，开展T 梁翼板正应力横向分布规律的理论与试验研究，明确胶合木T梁翼板的有效工作宽度，以利于工程应用。