不定积分的运算技巧
陈 飞
(商丘职业技术学院,河南 商丘 476100)
引言
不定积分是高职院校数学课程的核心,也是微积分的重要内容.不定积分的计算方法多种多样,其中换元积分法和分部积分法是重点和难点,学生在学习时有一定困难,且不能熟练地运用各种计算方法.合理的运用不定积分计算方法可以降低求解问题的难度.本文针对常用的解题技巧进行分析探讨,并结合具体例题进行讲解.
1 求解方法概述

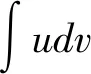
2 例说相关技巧
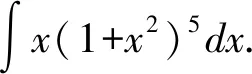
分析:可以通过凑微分,把积分变量凑成d(1+x2),用新变量u替换1+x2.
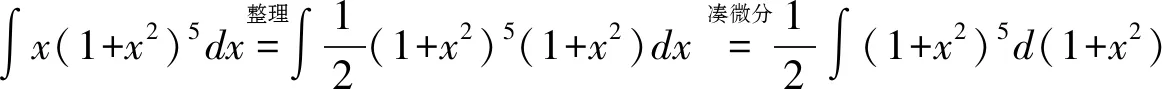
设u=(1+x2),于是:
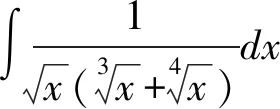
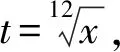
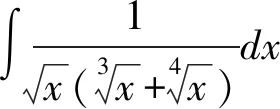
技巧: 运用第二换元积分法,关键是选择合适的变量代换函数小x=φ(t).对于x=φ(t),要求单调可微,且φ′(t)≠0,其中t=φ′(x)是x=φ(x)的反函数.

分析:为了去掉根号,可以引入关于未知量t的三角函数替代x,从而简化计算.
解:令x=atant,则dx=asec2tdt,于是:
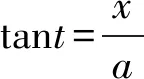
分析:被积函数为幂函数和反三角函数的乘积,故把反三角函数选作u,即u=arcsinx,则dv=xdx.



分析:在计算不定积分时,针对题目的特点可以多次使用分部积分法.
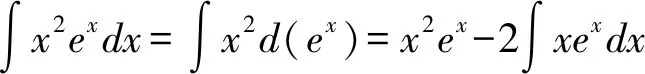

=x2ex-2xex+2ex+C.
分析:可以先采用换元积分法,再采用分部积分法进行求解.
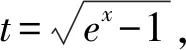
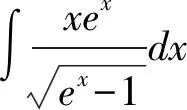

=2tln(1+t2)-4t+4arctant+C
解法一(凑微分法):

=cscx-cotx+C
解法二(分部积分法):
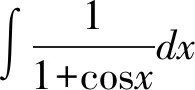

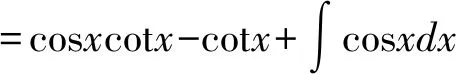
=cosxcotx-cotx+sinx+C
解法三(第二换元积分法):

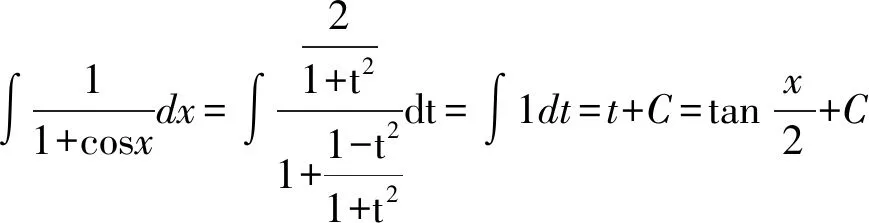
技巧:以上3种解法得出的解的形式是不同的,但是,解得本质是一样的,通过变换可得:
cosxcotx-cotx+sinx+C=cscx-cotx+C
根据不同的求解方法,求解出来的积分结果的形式是不一样的,但是,这些结果是正确的.我们只需对所求的结果进行求导,看是否等于被积函数[5].
解法一(换元积分法):

解法二(凑微分法):


解法三(代数换元法):
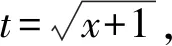

解法四(分部积分法):
3 结 语
不定积分的求解方法灵活多变,我们可以针对不同的被积函数类型,采取最有效的求解方法计算出不定积分.通过学习不定积分的运算技巧,可以培养学生的数学思维,增加学生的数学素养,从而提高分析和解决问题的能力.在求解不定积分时,合理地运用计算方法,并对所求的结果进行检测,从而熟练掌握不定积分的运算技巧.

