混合核函数相关向量机在污垢预测中的应用

解红刚，解红永，杜雅君，谭富军，梁金龙

（1.内蒙古超高压供电局，内蒙古 呼和浩特010080；2.国网天津静海供电有限公司，天津 300000）

0 引言

在当今工业化生产过程中由于换热设备结垢而造成的损失是巨大的，Steinhagen等人对新西兰上千家企业的3 000台各种类型换热器的通信调查表明，90%以上的换热器都存在不同程度的污垢问题［1］。污垢是指在与流体相接触的固体表面上逐渐积聚起来的固态物质，通常以混合物的形态存在［2］。根据西方发达国家调查，换热设备污垢给工业发达国家所造成的损失平均占国民生产总值的0.3%。对于发展中国家，由于技术、设备本身相对比较落后，以及环境污染对冷却水介质造成的严重污染，由污垢造成的损失更严重。减少污垢危害也是对倡导发展低碳、节能经济的有效支持。

污垢的形成是极其复杂的过程，影响其形成的因素众多。对污垢的研究主要包括3个部分：污垢预测、污垢监测以及污垢对策。污垢预测，是污垢监测和污垢对策的基础。从80年代，Epstein通过矩阵对污垢形成的过程的理论分析和实验研究做了概括［3］，到近年来，灰色理论，神经网络，模糊理论等各种算法在污垢预测中应用，虽然取得了很大的成果，但仍然存在着一些不足。

支持向量机（Support Vector Machine，SVM）是在20世纪90年代由Vapnik等人提出来的基于小样本统计学理论的机器学习算法［4］。SVM克服了其他智能算法的一些缺点，但也存核函数选取必须满足Mercer条件等不足之处。SVM中核函数的选取通常局限于某单一的核函数，并非局部核函数就是全局核函数，有一定的限制性。而混合核函数既有局部核函数的强插值能力以及善于提取局部样本的特性，又吸取了全局核函数善于提出全局样本的特性［5］。李可军、徐延顺等人将混合核函数应用到变压器顶层油温预测模型的建立［6］。

相关向量机（Relevance Vector Machine，RVM）是Tipping M.E.在2001年基于贝叶斯框架下提出的［7-9］。相对于SVM，RVM不仅可以获得二值输出，而且可以概率输出。在核函数的选取上RVM不受Mercer条件限制，而且RVM的训练样本时间比较短。段青、赵建国等人将组合核函数相关向量机应用到电力负荷预测［10］。陈程、聂德鑫等人基于支持向量机对变压器故障进行诊断［11］。将混合核函数和相关向量机相结合，把基于混合核函数的相关向量机应用到换热设备污垢预测中。

1 混合核函数相关向量机

1.1 混合核函数

支持向量机被广泛应用主要依靠于两项关键技术。第一，利用结构风险最小化（Structural Risk Minimization，SRM）原则设计具有最大间隔最优分类面；第二，通过核函数实现在高维特征空间的线性最优分类面，并可以实现输入空间的非线性学习算法。核函数就是利用非线性变化Φ将一个n维矢量空间中的随机矢量x映射到高维特征空间，在高维特征空间设计线性学习算法。

假定模式x属于输入空间X，既x∈X，通过映射Φ 将输入空间映射到一个新的空间 F=｛Φ（x）：x∈X｝，F称作特征空间。

给定一个函数z：X2→Z（Z为复数集C或实数集R）和模式 x1，…，xm∈X，则 m×m 矩阵 Zij=z（xi，xj）称为关于xi，…，xm的Gram矩阵。

一个m×m矩阵K是正定矩阵，当且仅当对于∀ci∈C均有。

令X为一非空集合，k是定义在X×X上的函数，如果k满足对所有的m∈N和x1，…，xm∈X都产生一个正定Gram矩阵，则称其为正定核，简称核。

设（X，μ）是一个有限测度空间。如果 k∈L∞（X2）是一个对称实值函数，则由其构造的x的平方可积函数的积分算子为

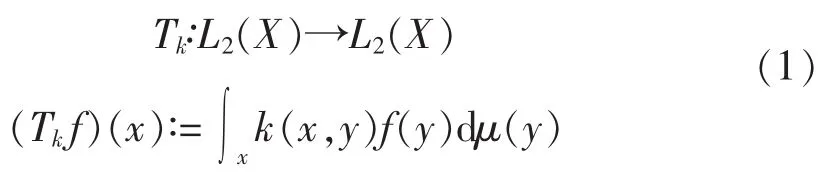
是正定的，即∀f∈L2（X），x∫k（x，y）f（x）f（y）dμ（x）μ（y）≥0。

常用的核函数包括：

1）高斯核函数

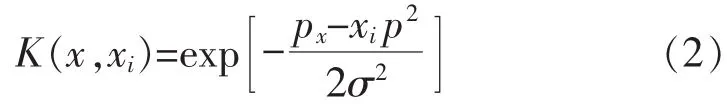
2）多项式核函数

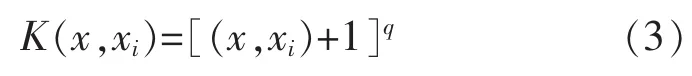
3）Sigmoid 核函数

4）线性核函数

常用的局部核函数是高斯核函数，高斯核函数对样本距离与σ相近的一定领域内的样本产生影响。然而当样本之间距离比σ大时，值就会趋于0。高斯核函数能很好地提出样本的局部特性。全局核函数经常采用多项式核函数，主要用于提取样本的全局性。Km表示混合核函数，Kl表示局部核函数，Kg表示全局核函数。

其中，α+β=1。

1.2 相关向量机

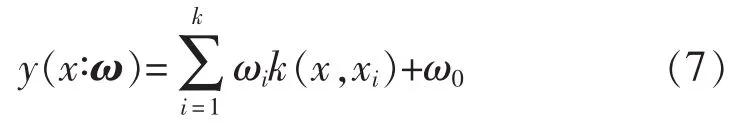
式中：N 为样本数；ωi为权值；k（x，xi）为核函数。

因此预测值为

式中：ε为附加噪声，且服从方差为σ2、均值为0的独立分布。已假设ti为独立分布，则

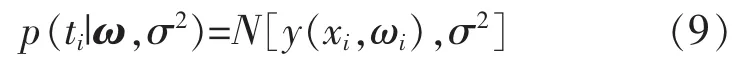
因此全体样本的似然函数为

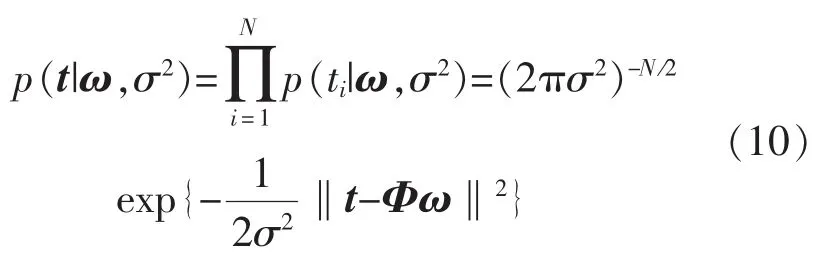
式中：t=（t1，…，tn）T，ω=（ω0，…，ωN）T，Φ＝［φ（x1），…，φ（xn）］T，φ（xi）＝［1，k（xi，x1），…，k（xi，xN）］T。

为避免过学习，权值ω赋予先验概率分布：

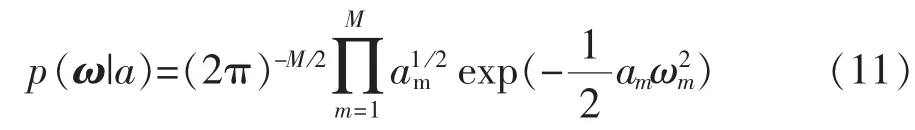
由先验概率、似然分布，则ω的后验概率分布：

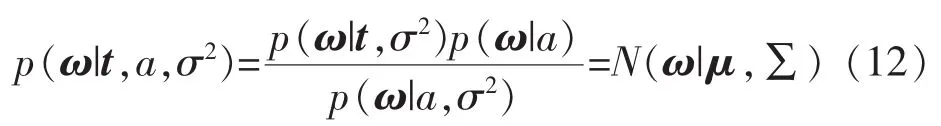
式中：μ=σ-2ΣΦTt， Σ＝（σ-2ΦTΦ+A）-1，A＝diag（a0，a1，…，an）。为了估计超参数的最佳值，超参数的似然分布为

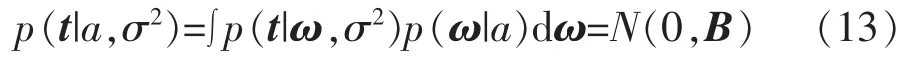
其中B＝σ2I+ΦA-1ΦT。超参数的更新为：

2 混合核函数相关向量机应用于污垢预测

2.1 样本数据采集

在对污垢形成过程的研究中发现，污垢热阻能反映出污垢的结垢程度。将污垢热阻值作为目标输出量，通过分析大量实验数据得出，能影响污垢热阻值的变量包括：污管的出入口温度、污管3个不同位置的壁温，污管内流体的流速。将这些变量作为输入自变量，污垢热阻值作为输出因变量，利用双管双回路新型污垢特性在线监测装置——污垢热阻动态模拟自动监测装置［12］采集数据。每1 min采集一组样本数据，连续采集1 700组数据。其中用前1 000组数据作为训练样本，全部数据作为预测验证，样本数据通过MATLAB归一化处理。

2.2 参数设置

混合核函数中Kl取高斯核函数，Kg取多项式核函数。其中 q＝1，α＝0.9，β＝0.1。分别用混合核函数、高斯核函数、多项式核函数做实验进行对比。混合核函数宽度为0.33，高斯核函数宽度为0.3，多项式核函数宽度为1，并且为二次多项式。超参数和方差的初始值为 initAlpha＝（1/N）2，initBeta＝var［t］×0.1。

2.3 评价依据

回归预测结果的好坏可以通过多种方法来进行验证。通过平均相对误差（RMS），均方根误差（RMSE）来评价：

3 实验结果和分析

实验所用样本数据为1 700组，分别通过混合核函数、高斯核函数、多项式核函数的相关向量机，在MATLAB7.1环境下进行仿真实验。

图1为实际污垢热阻值曲线。图2，图4，图6分别为混合核函数RVM，高斯核函数RVM，多项式核函数RVM下的实际曲线与预测曲线对比图。图3，图5，图7分别为对应核函数相关向量机下的相对误差曲线。

图1 实际污垢热阻曲线

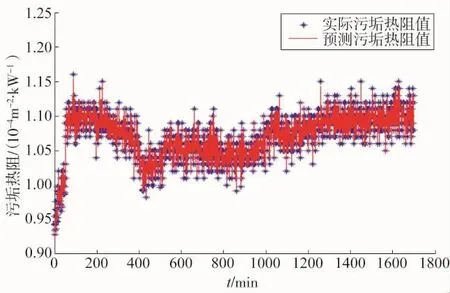
图2 混合核函数下的实际曲线与预测曲线对比

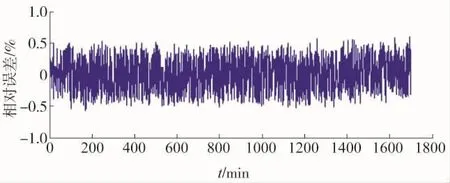
图3 混合核函数下的相对误差曲线

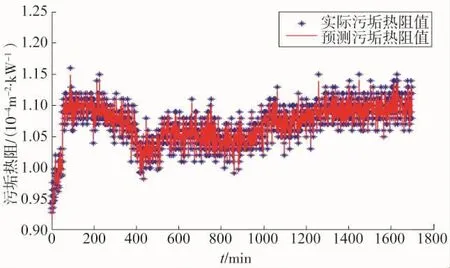
图4 高斯核函数下实际曲线与预测曲线对比

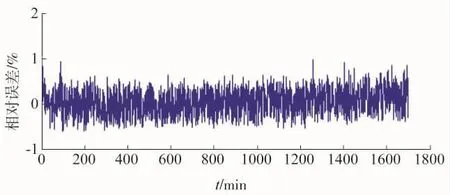
图5 高斯核函数下相对误差曲线

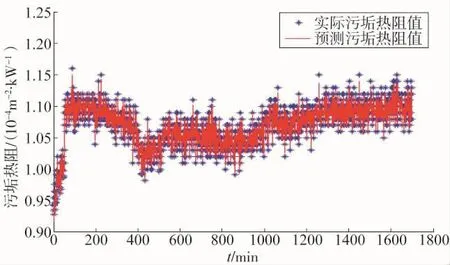
图6 多项式核函数下实际曲线与预测曲线对比

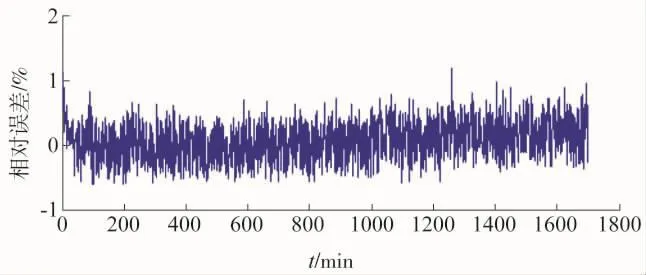
图7 多项式核函数下相对误差曲线

从图中可见，各个核函数下相关向量机都准确预测了污垢热阻值的曲线走势。相对于图4和图6，图2预测的效果更好。图3，图5，图7分别为对应核函数相关向量机下的相对误差曲线。相对于图5和图7，图3的相对误差范围更小。

表1列举了混合核函数相关向量机、高斯核函数相关向量机、多项式核函数相关向量机下的平均相对误差和均方根误差的实验结果数据。由表1可知混合核函数相关向量机的平均相对误差、均方根相对误差都要小于单一的核函数相关向量机。

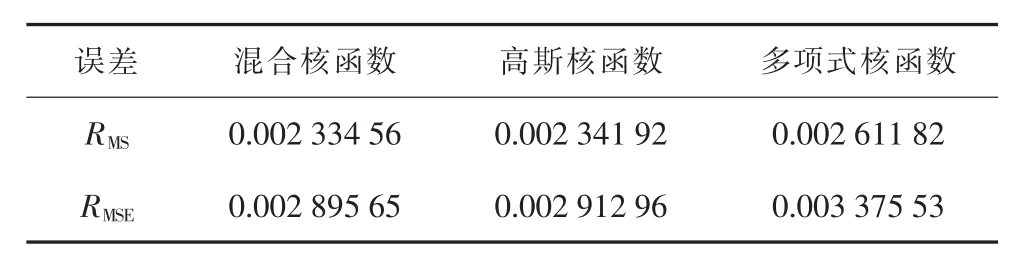
表1 实验结果统计

4 结语

基于混合核函数的相关向量机在换热设备污垢预测中取得了较好的预测效果，并且相对于某单一的核函数相关向量机，混合核函数相关向量机的预测精度更高。

混合核函数相关向量机相对单一核函数相关向量机虽然取得了较好的预测效果，但依然存在问题。混合核函数中的各单一核函数的选取依据没有，而且混合函数的参数比单一核函数参数要多，以致有时候构造的混合核函数不如单一核函数效果好。混合核函数中各单一核函数所占的比重也是一个需要考虑的问题。

相对于以往的SVM，RVM的输出更多样化，不仅有二值输出，也有概率输出以及置信区间输出。然而随着输入样本的复杂，RVM的训练时间将加长，如何降低RVM在复杂输入的样本训练时间，将是今后的研究方向。