基于偏序集的采空区塌陷危险性评价研究*
黄 亮,王会敏,2,岳立柱,金 珊
(1.辽宁工程技术大学 矿业学院,辽宁 阜新 123000;2. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819; 3. 辽宁工程技术大学 公共管理与法学院,阜新转型创新发展研究院, 辽宁 阜新 123000)
0 引言
目前,我国多数矿山以空场法方式开采,加之早期民采泛滥,形成了大量采空区。由于采空区塌陷具有突发性、随机性、隐藏性等特点,大部分采空区未能得到有效治理。随着开采条件不断恶化,采空区经常出现冒落与地压活动,矿柱、顶板发生破裂变形甚至失稳破坏,进而诱发地面塌陷、采空区冒顶片帮、地裂缝、岩石崩塌等灾害,给矿山生产与安全带来了极大隐患[1-2]。因此,如何保证矿山的长期安全运行、安全事故及灾害不再发生,是采空区塌陷预防与防治的首要问题,而科学合理地进行采空区塌陷危险性评价对于研究采空区整体稳定性具有重大的社会效益与现实意义[3]。
近年来,国内很多学者在采空区塌陷危险性评价领域进行了深入研究,其方法主要体现在5个方面:1)应用可拓学理论建立评价模型。如赵超等[4]将层次分析与可拓理论结合建立了采空区塌陷危险性物元综合分析模型,通过对采空区样本数据的分析,评定采空区塌陷危险等级并提出合理的应对措施。2)应用未确知测度理论。如宫凤强等[5]基于未确知测度理论,利用熵计算指标权重,依照置信度识别准则评定等级。3)模糊综合评价方法。如陈建[6]应用模糊系统基本理论建立了采空区塌陷危险性评价模型,依据最大隶属度原则确定评定等级。4)灰色关联分析法。如王新民等[7]分析指标并确定其权重,应用灰色关联理论计算出关联度,进而评定采空区塌陷危险度。5)神经网络分析法。如冯岩等[8]将主成分分析法与神经网络相结合建立了采空区塌陷危险性评价模型。
以上几种常用方法可以分为2大类,即等级贴近度模式和样本自分类模式。方法1)~4)属于等级贴近度模式,即凭借专家经验给出危险等级,基于不同的理论进行等级归类。该模式能够充分发挥专家的经验,但较为主观,缺乏一般性,同时忽视了数据本身蕴含的信息。此外,其所选择的赋权方法存在误区和争议。方法5)属于样本自分类模式,即以样本期望值为界限划分危险等级,其适用性较强,但较为客观,缺乏独特性,忽略了专家经验,使评价结果缺乏可信度,同时对样本量的依赖性较强,样本量不足会导致其无法应用。综合考虑以上2种模式的优缺点,拟采用偏序集理论对采空区塌陷危险性进行评价研究,在解决赋权争议问题的同时兼顾主客观问题,以期准确判别采空区塌陷的危险程度,为灾害事前的预防控制提供新思路。
1 采空区塌陷危险性评价指标
评价结果是否准确很大程度取决于评价指标的选取是否科学、合理。不同的学者运用各自的理论方法,选择不同的评价指标对采空区塌陷危险性展开评价。赵超等[4]、宫凤强等[5]、陈建[6]、王新民等[7]选择相邻空区情况、岩体结构、埋藏深度、地质构造、地下水、采空区面积、矿柱尺寸及布置、岩石质量指标、跨度、高度等评价指标;张连杰等[9]主要从采空区的覆盖层类型、采空区埋深、地质条件、开采技术条件等方面选择指标;陈洪江等[10]考虑采空区特点、地质构造、矿层特点、采空区叠置等方面确定评价指标体系。以上研究从不同角度建立了评价指标体系,但无论从哪个角度研究,采空区发生塌陷都有一定程度上的共同因素存在:地质因素,包括地质构造、岩体结构、岩石质量指标等;水文因素,包括地下水、降雨量等;采空区参数因素,包括采空区面积、矿柱尺寸、埋深、跨度、高度等;环境因素,包括相邻采空区情况、外界扰动等。
判断采空区塌陷危险度的最基本因素:相邻采空区情况(包含其密集程度与影响面积大小2方面),采空区太密集易形成采空区群,如果采空区面积较大,会产生明显的宏观地压现象,导致大面积的地表塌陷、矿柱垮落,严重影响采空区的稳定状态;地质构造发育部位不仅对地层完整性产生破坏,同时还会穿越隔水层,形成良好的导水通道,使其稳定性更差,更易发生破坏,从而产生地面塌陷;岩体结构与岩石质量情况影响采空塌陷强度大小,其顶板岩体强度高低直接反映采空塌陷变形程度甚至破坏程度,顶板岩体完整性差、节理裂隙发育,更易发生冒落、崩坍等现象;地下水不仅降低岩石强度,若采空区顶板含水层发育会使其力学强度变低,有利于采空塌陷发育;矿柱留设与布置起到支护与防治塌陷的作用,矿柱及顶板岩石承重压力过大,容易破坏矿柱或顶板岩层,若矿柱严重损坏或布置不合理会直接影响地表塌陷;形成的采空区埋深越大时,地压活动越明显,岩体移动和破坏也更加明显;当采空区跨度、高度越大时,冒落带、导水裂隙带就越大,上覆岩层在纵向的变形范围就越大,采空区也越不稳定。
综上所述,本文选取10项最基本因素作为采空区塌陷危险性评价指标,即相邻空区情况、岩体结构、埋藏深度、地质构造、地下水、采空区面积、矿柱尺寸及布置、岩石质量指标、跨度、高度(分别用X1,X2,X3,X4,X5,X6,X7,X8,X9,X10表示)。
2 采空区塌陷危险性的偏序集评价模型
2.1 偏序集理论与评价模型[11]
给定评价模型U=(A,IC,H),评估关系模型M=(A,R),其中A={a1,a2,…,am}为评估对象或方案集;IC={c1,c2,…,cn}为评价准则集;H={hk:A→Vk|k=1,2,…,m}为评估对象与评估准则之间的关系集;R为评估对象之间的关系集,表示xi与xj的一个二元关系,且满足:
1)自反性:对任意x∈A,有XRX;
2)反对称性:对任意x,y∈A,若XRX且YRX,则x=y;
3)传递性:对任意x,y,z∈A,若XRY且YRZ,则XRZ
则称R为A上的偏序关系。
对于含有m个样本n个指标的决策问题,岳立柱等[12]根据各指标重要程度的优劣次序,即偏序集(A,⪯)各准则权重秩次w1≥w2≥…≥wn,用矩阵形式表示蕴含权重信息的方案决策问题:



若矩阵G中的第i行大于或等于第j行,则对应方案Ai优于或等于方案Aj。由此,经过累加变换,得到累加变换矩阵并逐行比较,构造出蕴含权重信息的比较关系矩阵,即给定偏序集(A,⪯)。对于 ∀ai,aj∈A,若aj⪯ai,记rij=1;若ai⪯aj或者aj与ai不可比,记rij=0 ,称R=(rij)mn为(A,⪯)的比较关系矩阵。由比较关系矩阵得到Hasse矩阵,范懿[13]给出了比较关系矩阵和Hasse矩阵之间的转换公式:
HR=(R-I)-(R-I)*(R-I)
(1)
式中:R为关系矩阵;HR为Hasse矩阵;I为单位矩阵;*为布尔运算。
再由Hasse矩阵绘制Hasse图。Hasse图是研究偏序集理论的强有力工具,表示有限偏序集的一种数学图表,能够通过图形充分展示方案间的传递关系、结构关系,使得决策者能够直观、准确地把握综合排序的分层和聚类情况。
2.2 评价步骤
1)确定指标集;
3)指标数据无量纲化处理;
4)获取指标权重排序信息;
5)通过计算得出Hasse矩阵;
6)绘制Hasse图,对方案进行分类和排序;
7)结果分析,若偏序满足精度则停止计算,否则应用秩均值的近似计算公式[14]:
(2)

3 应用实例
大宝山矿业有限公司铜业分公司井下采用空场法开采,而且民采泛滥。在开采区段11~57线沿走向2 000 m地段形成了大量的采空区, 致使井下地压活动频繁,常发生矿柱开裂破坏、冒顶。该区不仅发生过多起采空区灾害事故[6],还多次发生大型冒落和地压活动,对矿井安全生产造成了严重的威胁和破坏。根据铜业分公司提供的相关资料,知采空区分布最为密集的区段为39~49线及 25~31线,且其面积较大。随着向深部开采延伸,采空区体积呈增长趋势,尤其610,570中段采空区最为集中。其井下采空区实际情况[15-16]如表1所列。
3.1 采空区危险性评价指标分级标准
采空区塌陷评价指标的危险性分级缺乏统一标准,且不同采空区的地质情况、水文情况、采空区参数等因素都存在差异。由于不同采空区的评价指标会随着具体情况的变化而改变,那么评价指标的权重大小和危险性等级划分区间自然也有所不同。
①随开采水平的延伸,特别是进入三水平戊二、丁二采区后,煤层变薄(煤厚2m左右),断层增多,煤层内在灰分明显增高,煤质变差。②下分层采、掘工作面的增加,回采、掘进时,采掘头面顶板压力大、破碎,掉、冒顶矸石造成外来灰分的增加,严重影响到矿井毛煤质量。③随采掘机械化程度的提高,掘进工作面设计高度一般在2.6~2.8m,受煤层厚度的影响(煤厚2m左右),掘进工作面施工时,出现多破矸石现象,造成了灰分的增加。

表1 井下采空区实际情况Table 1 Actual situation of underground goaf
本文利用文献[4]中的实例数据来验证偏序集评价模型的可行性。实例原始数据如表2所列。文献[4]~[5]的实例数据均源自文献[17],因此,引用文献[4]~[5]中的等级划分标准,将采空区塌陷危险性等级划分为极度危险、高度危险、中度危险、轻度危险,分别用{Ⅰ,Ⅱ,Ⅲ,Ⅳ}表示(见表3、表4)。
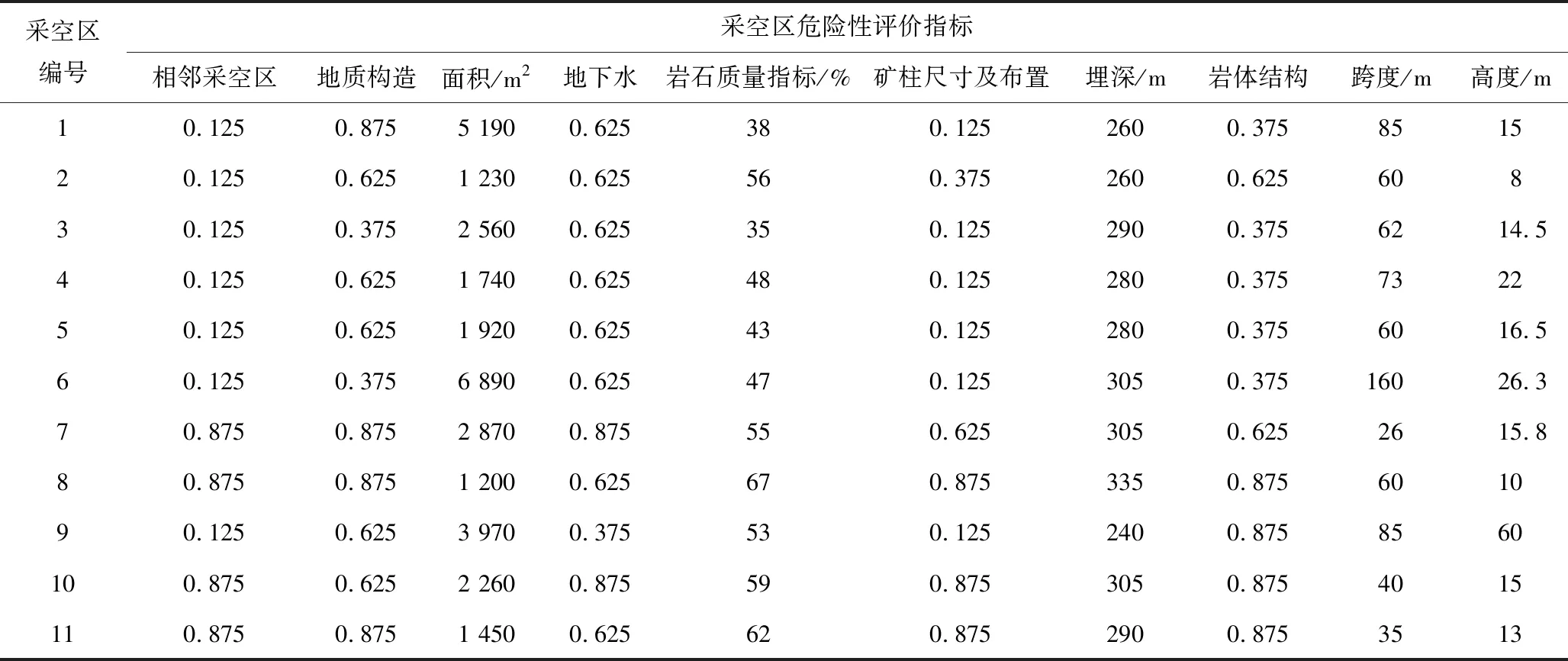
表2 原始数据Table 2 Statistical table of goaf collapse risk evaluation index survey

表3 采空区危险性评价的定性指标分级标准及赋值Table 3 Classification criteria and values of qualitative indexes for goaf risk assessment

表4 采空区危险性评价的定量指标分级标准Table 4 Quantitative index classification criteria for goaf risk assessment
3.2 数据处理
偏序集决策是通过准则建立方案间偏序关系,进而对方案进行选择与排序的多准则决策分析方法。依据方法原理构造“等级标准训练样本”以明确层集间的优劣标准,确保更为精度的分级评价。本文采用等间距均匀分布方式,内插各评价指标等级标准值。由于各评价指标值是以实际野外勘察及前人资料综合分析为基础得到的,故对各指标进行插值所得到的训练样本也应该符合研究区的采空区塌陷特点。以采空区塌陷Ⅰ级危险等级,X1指标插值为例:指标X1在0~0.25范围内处于Ⅰ级危险区,将0~0.25范围划分为等间距的4等分,即所插值的点为0.062 5,0.125,0.187 5;加上左端点值0(值得注意的是右端点值0.25为指标X1在0.25~0.5范围内的左端点取值,以避免2个等级取值的信息重合),共计4个Ⅰ等级标准样本点;同理,指标X1在0.25~0.5区间的样本点分别为0.25,0.312 5,0.375,0.437 5,共计4个Ⅱ等级标准样本点;在0.5~0.75范围的样本点分别为0.5,0.562 5,0.625,0.687 5,共计4个Ⅲ等级标准样本点;在0.75~1范围的样本点分别为0.75,0.812 5,0.875,0.937 5,1,共计5个Ⅳ等级标准样本点。以此类推,获得其余各指标插值,且将构造的17个等级标准训练样本按危险程度从大到小依次编号为12,13,…,28。

3.3 指标权重排序
各项评价指标的权重秩序直接影响评价结果的准确性。本文指标的重要性排序来自文献[4],将指标数据按照权重的秩序依次排序,得到蕴含权重的累加指标数据。
3.4 Hasse矩阵
对累加变换矩阵行向量进行比较,若aj⪯ai,记rij=1;若ai⪯aj与aj与ai不可比,记rij=0,得到累加指标数据的比较关系矩阵R=(rij)mn。根据式(1)给出的比较关系R和Hasse矩阵的矩阵变换方式得到Hasse矩阵。
3.5 Hasse图
通过Hasse矩阵可绘制Hasse图(见图1)。通过Hasse图能够直观地体现出各个采空区间的聚类信息,方便对比分析。

图1 采空区塌陷危险性Hasse图Fig.1 Hasse diagram of goaf collapse risk
3.6 结果分析
基于图1,可以直观地把握各样本危险性的分级与聚类信息。偏序集理论具有上集研究案例优于下集研究案例的特点(如A8指向A7,表示A8优于A7),且具有传递性。因此在图1中,越是位于图上端的节点群体表示的采空区塌陷危险性越小。根据构造的“等级标准训练样本”,可以将28个样本从下往上依次划分为4个危险等级群:
1)第1等级群(极度危险):12,13,14,15;
2)第2等级群(高度危险):16,17,18,19,6,3,9,1,4,5;
3)第3等级群(中度危险):20,21,22,23,2;
4)第4等级群(轻度危险):24,25,26,27,28,7,10,11,8。
具体表述为:在28个样本中,12~28是按照原等级标准人为构造的虚拟样本。根据图1可知,样本28,27,26各自为一层,样本11,8与虚拟样本25处于同一层集,样本7,10与虚拟样本24处于同一层集,样本7,10,11,8与虚拟样本24,25,26,27,28组成危险Ⅳ等级群,表示各样本对应的采空区危险程度为轻度危险;同理可以判断出,样本2与20,21,22,23组成危险Ⅲ等级群,表示各样本对应的采空区危险程度为中度危险;样本6,3,9,1,4,5与16,17,18,19组成危险Ⅱ等级群,表示各样本对应的采空区危险程度为高度危险;样本12,13,14,15组成危险Ⅰ等级群,表示各样本对应的采空区危险程度为极度危险。

其中危险性最大的为570中段6号采空区,这与其实际状况(6号采空区处于岩体碎裂、褶皱的地质条件下,且其面积最大,周围采空区分布集中,跨度最大)是一致的;采空区危险性最小的为542中段8号采空区,该采空区实际状况(8号采空区开采面积最小,地质构造简单,无断层褶皱影响,工程布置规范,岩体结构为完整的块状结构,具有很好的抗剪抗压强度)也是一致的。实际上,同时处理大量的采空区问题在时间和人力上是不现实的,因此根据采空区危险性排序,科学合理地选择性处理高危采空区,可以为采空区安全生产与治理提供科学的指导意义,同时也有利于决策者针对采空区内不同位置的实际情况制定相应的防治措施,具有理论与应用价值。

表5 数值及排序结果Table 5 Values and sorting results
通过对比分析:本文方法所得到的分析结果与文献[4]运用层次可拓法,文献[5]运用未确知测度理论所得到的分析结果是一致的,同时本文方法与文献[4]~[5]相比有3方面的独特之处:
1)本文方法只需得知权重顺序,不拘泥于具体权重大小值,解决了赋权争议问题,而文献[4]~[5]需要精确的权重,从操作层面与赋值方式上本文方法更为简洁,避免了精确赋值的困扰。实际上,绝大多数计算权重的方法获得的权重顺序基本上是一致的,只要该赋权方法能有效地提取相应的权重顺序即可推广应用。同时在分析复杂度较高与信息模糊不全决策问题时,可以通过专家获取权重排序,解决没有具体权重数值而不能应用的模型问题。
2)能够体现样本间的分层信息。用Hasse图对样本排序与分类过程能够展示更为丰富的信息,能看见样本间的层次关系。可以将样本分成多个层次,层次的高低代表其差异性大小,层次越大差异性越明显。可以看出本文28个样本分成了4个等级群,且从上往下看第Ⅳ等级群优于第Ⅲ等级群,第Ⅲ等级群优于第Ⅱ等级群,第Ⅱ等级群优于第Ⅰ等级群,即{A28,A27,A26,A25,A24,A11,A10,A7,A8}≻{A23,A22,A21,A20,A2}≻{A19,A18,A17,A16,A1,A4,A5,A9,A3,A6}≻{A15,A14,A13,A12}。
3)能够识别排序的稳定程度。如方案A11优于方案A10,方案A10优于方案A5,方案A5优于方案A3,方案A3优于方案A6等可比关系,只要各指标的权重排序不变动,则28个样本的偏序结构就不变。无论权重大小怎么变动,原可比关系保持不变,防止了权重仿真过程发生,充分说明了偏序集分析方法具有良好的鲁棒性。
4 结论
应用偏序集方法对采空区塌陷危险性展开评价,在现有指标基础上,根据相关文献提取指标,应用偏序集解决了赋权争议问题,提出了一种更为稳健的评价方法:
1)本质上,偏序集方法的优越性体现在指标合成过程中,其用一个权重空间代替权重向量,这个权重空间只需通过专家对指标的一个定性分析就能获取,即获取权重排序。获取权重顺序相对简单,因此,相比以往方法其操作简单,同时更为稳健,它们是无限个权重合成的结果。
2)实际上,本文方法不仅可以扩展本文研究的线性模型,其他矿区的危险性评价方法都可以用偏序集表示,只要赋权方法能够提取权重顺序信息即可应用。
3)基于本文分析结果,利用偏序集评价方法准确地对各个采空区塌陷危险程度进行分层聚类及排序,将有利于负责矿井安全的相关部门准确判别采空区塌陷危险的可能性程度,并及时采取相应的综合治理措施,可有效预防采空区塌陷的发生,实现安全、高效生产。

