海洋立管内流流动分析及疲劳寿命预测*
骆正山,蔡梦倩
(西安建筑科技大学 管理学院,陕西 西安 710000)
0 引言
中共十八大及十九大报告中强调“海洋强国”战略,指出海底资源的开发将是我国能源发展的总趋势,但复杂多变的海洋环境使开采工程面临多方面的威胁,其中失效破坏多源于海洋立管涡激振动引起的疲劳破坏,因此准确预测立管的涡激振动在油气开发系统中占有重要地位[1-3]。现如今国内外学者已经开展了大量研究,Nguyen等用CFD仿真软件进行了圆柱涡激振动数值模拟,研究表明三维圆柱体数值模拟模型更接近涡激振动实际工况特性[4];Huera-Huarte.F.J等对立管模型进行实验研究,发现涡激振动顺流向的响应对立管疲劳的影响与横流向的振动响应在数量级上相当[5];翟云贺等基于SSTk-ω湍流模型采用RANS方法对立管运动轨迹及尾涡等特性进行了研究[6-8]。但实际工程中海洋立管内部有油气等流体的流动,复杂内流对立管涡激振动特性有着不可忽略的影响,而当前考虑内外流共同作用的立管涡激振动研究很少,Zhang[9]和郭海燕[10-11]等通过试验发现立管的振动会造成内流场流速和压强的波动,但也仅讨论了单自由度涡激振动,忽略了涡激振动中顺流向(In-Line,IL)和横流向(Cross-Flow,CF)的耦合作用,内流对立管涡激振动的影响还有待完善。
综上所述,研究基于Van Der Pol尾流振子模型,提出一个非线性立管涡激振动模型,不仅考虑横向和顺流向的耦合作用,也考虑内外流共同作用对立管的影响。进一步选用P-M准则对立管的疲劳寿命进行分析,通过编程和实例计算,分析了管内流速对位移响应和疲劳寿命的影响。
1 基本理论及模型建立
1.1 柔性立管结构振子模型
深海立管通常认为是服从Euler-Bernoulli模型假定的抗弯弹性结构。选用Cartesian坐标系,x轴为顺流向,y轴为横流向,z轴为垂直方向,如图1所示。立管结构振动方程可表示为:
(1)
(2)
式中:E为弹性模量,N/m2;I是截面弯曲惯性矩,m4;c为结构阻尼系数;c′为等效流体阻尼系数;T为顶张力,N。
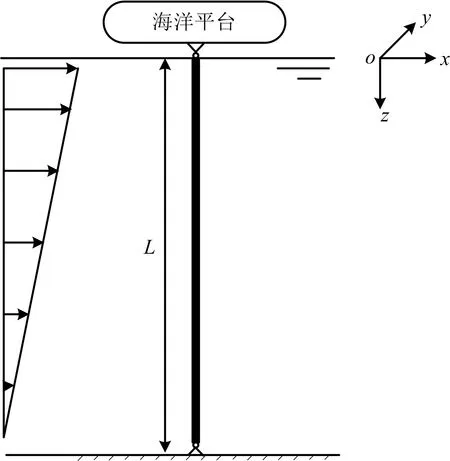
图1 立管模型示意Fig.1 Schetch of the riser model
该模型在结构静力平衡方程的基础上加上立管惯性力和阻尼力得到,但未考虑内流流动引起的荷载。基于此,考虑工作状态下油气能源通过一定曲率管道时产生附加荷载离心力和科氏力,并依据现行的海洋油气管道设计标准以及有关文献[12-17],提出了一个包含内流流速项和科氏力的立管涡激振动方程:
(3)
(4)
该模型在经典Euler梁基础上不仅考虑了内流质量的影响,更考虑到内流流速的影响,mi为单位长度管内流体质量,kg;v为内流流速,m/s。
在生产过程中,考虑到内流流动,有效张力及管道质量可表示为:
T=Tw-AiPi+A0P0-ρAiv2
(5)
(6)
式中,Tω为立管结构的轴向张力,N;Ai和A0为管道内径和外径所对应的截面面积,m2;Pi和P0为管道的内外压力,Pa;ρ为管内流体密度,kg/m3;mr为单位长度管道质量,kg;Cm为管道附加质量系数,一般取Cm=1;ρ0为管道环空流体密度,kg/m3;Dm为惯性力外径,m。
fx(z,t)和fy(z,t)分别为使立管在IL和CF方向上发生涡激振动的涡激力:
fx(z,t)=ADCDVrU
(7)
(8)

1.2 尾流振子模型
采用Facchinetti改进的Van Der Pol尾流振子模型模拟流体对立管的涡激振动作用力,该模型相比其他更加简便快捷,表示为:
(9)

1.3 数值求解
将立管长度从底端z=0到顶端z=L平均分成n份,共可得n个计算单元和n+1个节点,z=L处节点编号为0,沿z轴方向直到n。将式(3)、式(4)和式(9)方程耦合求解,采用Hermit插值函数离散求得矩阵表达式:
(10)
(11)
(12)
然后采用Newark-β方法,对矩阵方程组进行逐步积分,假设初始时刻t0的位移,速度和加速度已知,可求得t1时刻的位移,速度和加速度,依次推导得出所有计算时刻立管的动力响应值。
1.4 立管疲劳寿命
海洋立管固有频率一旦降低到“锁频”状态则会发生涡激振动,若管道长期处于这种交变应力则会造成疲劳破坏,而交变应力大小和立管涡激响应的振幅息息相关,因此内部流体的流动不仅影响着立管的振幅,对立管疲劳寿命也有一定的决定作用。研究选取P-M理论对海洋立管的疲劳寿命进行分析。
根据P-M线性累积破坏原则:
(13)
当Dt=1时,海洋立管将会破坏。式中:n(Δζi)表示立管涡激振动中遭受交变应变在Δζi范围内出现的周期数;N(Δζ)通过美国焊接协会所提出的S-N曲线计算,可表示为:
N(Δζ)=g·(Δζ)-e
(14)
式中:g=6.4×108,e=4。Δζ表示一个振动周期内的最大应变差,研究假设立管两端铰接,则最大应变差出现在管道中点,Δζ可表示为:
(15)
式中:H表示立管中点振幅,m。与之对应的循环周数为:
n(Δζi)=fiti
(16)
式中:fi表示第i种振幅的频率,Hz,ti表示所对应时间,s,从式(10)、(11)中计算求得。通过将式(14)、(15)、(16)代入式(13),可求得1年的Dt值,即:
(17)
式中:Hi为管道中点的第i种振幅,m,可由式(10)、(11)计算求得;式中ti总和表示t=1年立管振动的总秒数,研究为了方便分析选用年为单位,用Ti表示:Ti=ti/3 600×365,代入式(17)取倒数,即可得到立管的疲劳寿命:
(18)
2 涡激振动试验
在涡激振动试验水池(60 m×36 m×6.5 m)内进行了试验,试验装置见图2~3。立管模型总长6.3 m,上下两端为铰接,立管两端分别设置了进水管和出水管,选用高压自吸水泵对内流施加,水池自带造流系统可模拟均匀流,采用多谱勒测速仪测量外流速。试验为测得立管的应变时程响应,沿立管竖向选取11个测点,每个测点四周对称分布四个应变片采集数据,然后结合模态分解法处理试验数据。具体立管实体及模型参数如表1所示。

图2 试验模型及应变片布置Fig.2 Experiment model and strain sensor layout
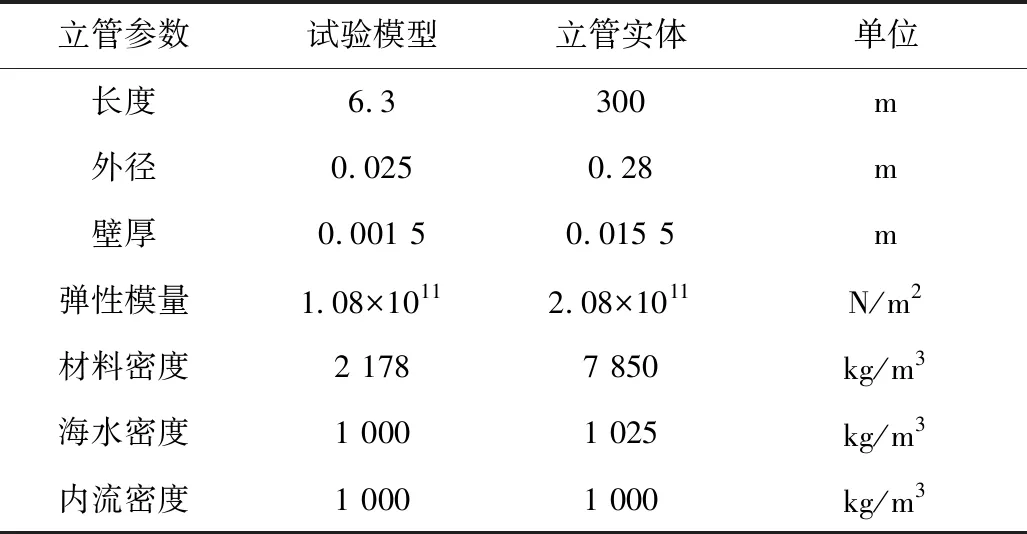
立管参数试验模型立管实体单位长度6.3300m外径0.0250.28m壁厚0.001 50.015 5m弹性模量1.08×10112.08×1011N/m2材料密度2 1787 850kg/m3海水密度1 0001 025kg/m3内流密度1 0001 000kg/m3
试验中主要考虑立管两端铰接固定的工况,与立管实际工况有一定程度的不同。为了更加准确研究柔性立管在实际作业情况下的VIV动态响应,在模型实验中考虑了顶端张力的影响。
3 试验结果与计算对比
使用表1中试验模型相关参数,采用海流流速U=0.35 m/s,内流流速V=0.3 m/s,以立管中点位移时程为例,结合式(3)~(12)进行相关理论计算,计算结果与试验测量数据对比分析如图3所示。
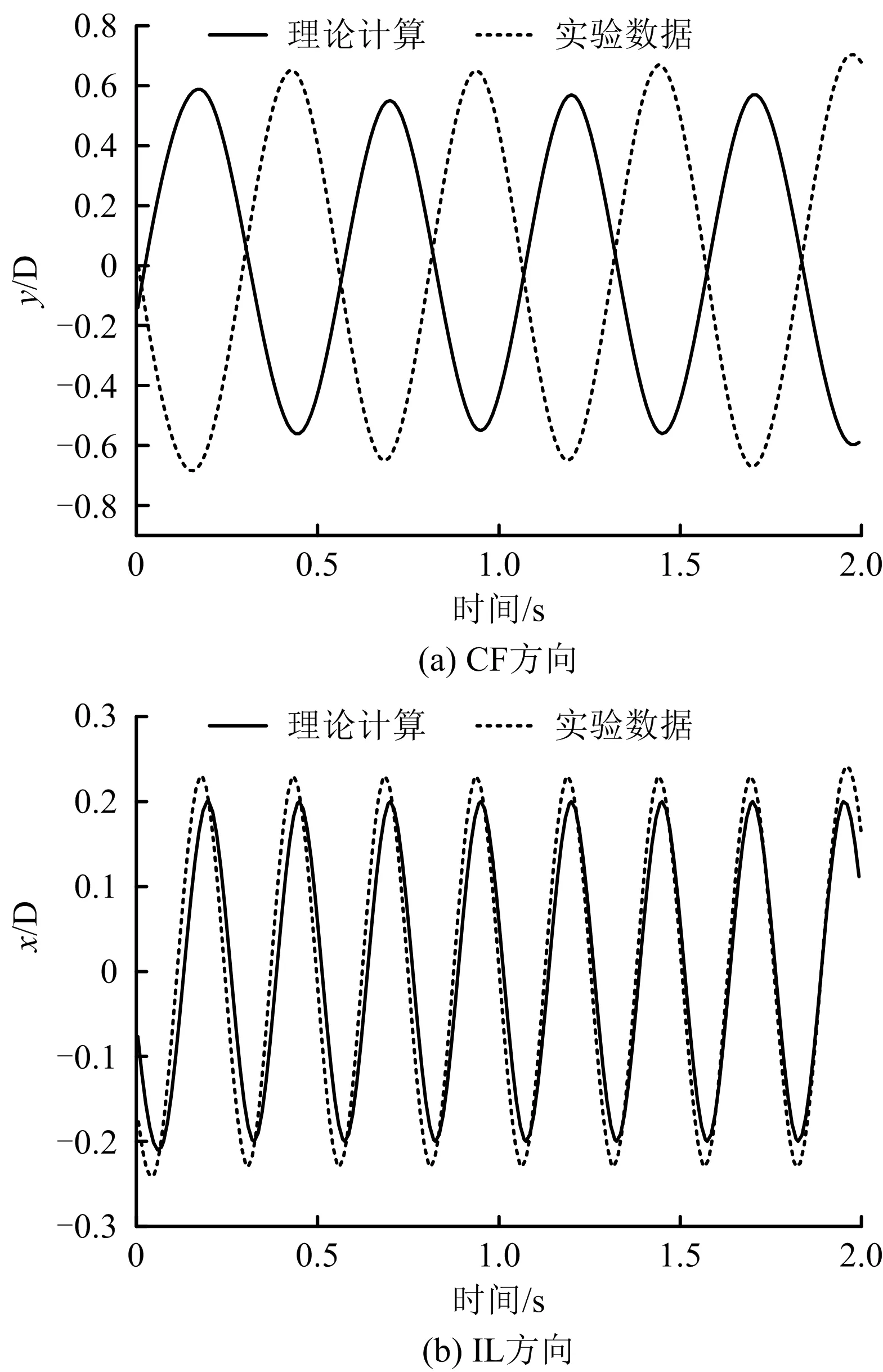
图3 立管中点位移时程曲线(U=0.35 m/s,v=0.3 m/s)Fig.3 Transverse time-series displacement at midpoint of riser under different internal and external speeds
可以看出在内外流共同作用下,立管CF和IL方向位移曲线与实测数据基本吻合,证明所建模型的是合理的,可以有效预测海洋柔性立管的涡激振动响应,也可为疲劳寿命分析提供保障。
4 实例计算
4.1 横向涡激振动下立管动力响应及疲劳分析
在海洋垂直面上海流的速度随海水深度的变化而变化,根据我国勘察的试采区,采用流速底端U=0.2 m/s,海平面U=0.5 m/s作为海洋环境条件,使用表1所列的立管几何参数进行分析。
1)振动响应
考虑管内流体的流动,按本文编制的计算程序计算立管在漩涡脱落时的动力响应,管内流体流速取以下4种情况:V=0 m/s,V=10 m/s,V=20 m/s,V=30 m/s。图4为立管中点在不同管内流速下时程曲线,图5为考虑管内流体的流动及顶张力和顶端压强的影响。
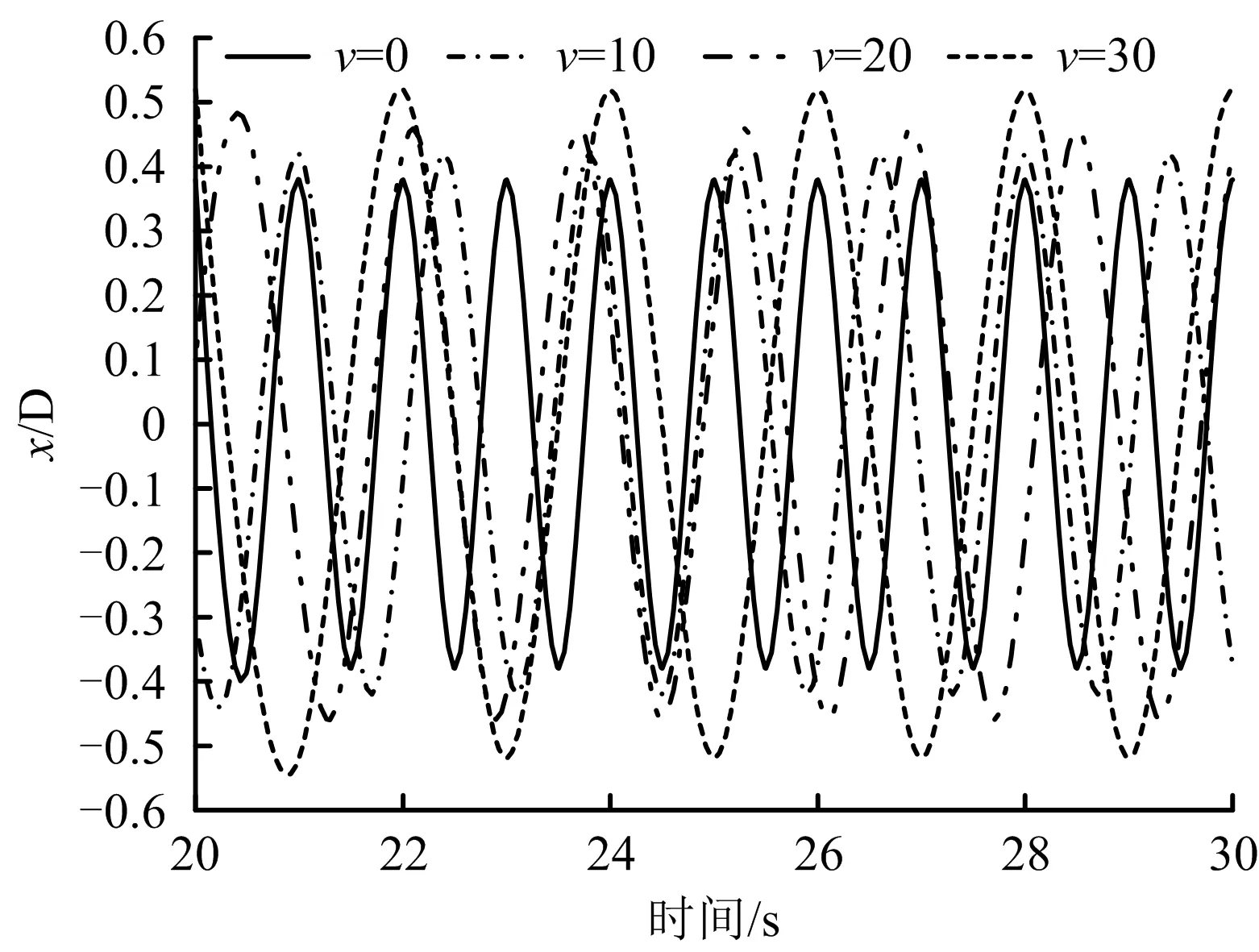
图4 不同管内流体流速下时间-位移曲线(z=150 m)Fig.4 Time-series displacement of riser under different internal speeds(z=150 m)

图5 不同顶张力下时间-位移曲线(z=150 m)Fig.5 Time-series displacement of riser under different top tension(z=150 m)
从图4可看出,当内流流速较低时,内流对立管振动幅值影响并不明显,但当内流流速较高时,振动幅值发生显著变化,并且振动频率降低可能使更多管单元降低到“锁振”频率范围,使立管产生动力放大,加速了立管的疲劳破坏,因此内流的影响应当重视。从图5可看出通过适当增加立管顶张力能有效消除由于管内流速对涡激振动造成的影响,但同时立管的应力也会相应增大,在实际工程中这一点不可忽略。
2)疲劳寿命
图6和图7为不同内流和不用顶张力下立管的疲劳寿命。可以得到:选取的4种不同内流流速对应的最短疲劳寿命为15.3,15.23,14.3和13.49 a,选取的3种不同顶张力对应的最短疲劳寿命为15.3,27.4和47.28 a。研究发现立管的疲劳寿命随着内流流速的增加在降低,内部流动流体除了影响立管的响应幅值,还会降低立管的疲劳寿命。随着顶张力的增加立管的疲劳寿命呈增大趋势,其主要原因是立管振动幅值的降低使输流管长期处于较低弯曲应力循环状态。因此通过增大顶张力消除涡激振动中内流对立管所造成的影响是切实可行的。

图6 不同内流流速下立管疲劳寿命Fig.6 The fatigue life of riser under different internal speeds

图7 不同顶张力下立管疲劳寿命Fig.7 The fatigue life of riser under different top tension
4.2 横向与顺流向耦合涡激振动下立管动力响应及疲劳分析
选取CF向涡激振动响应计算中底端流速U=0.2 m/s,海平面U=0.5 m/s为海洋环境,内流流速取V=10 m/s。图8和图9分别为横向与顺流向耦合涡激振动下立管中点位移时程曲线及疲劳寿命。
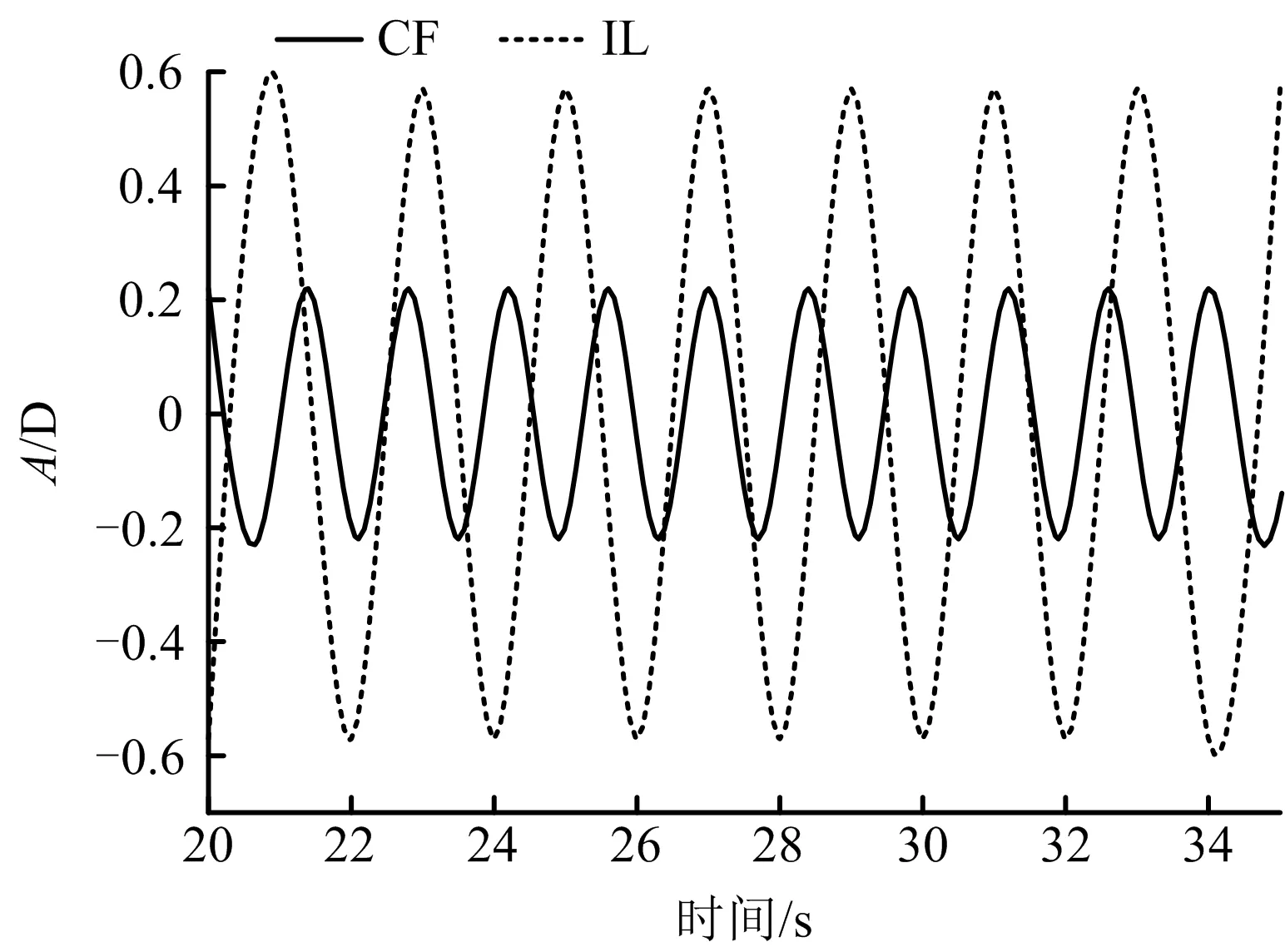
图8 立管横向和顺流向时间位移历程Fig.8 Time-series displacement of riser at the cross-flow and the in-line
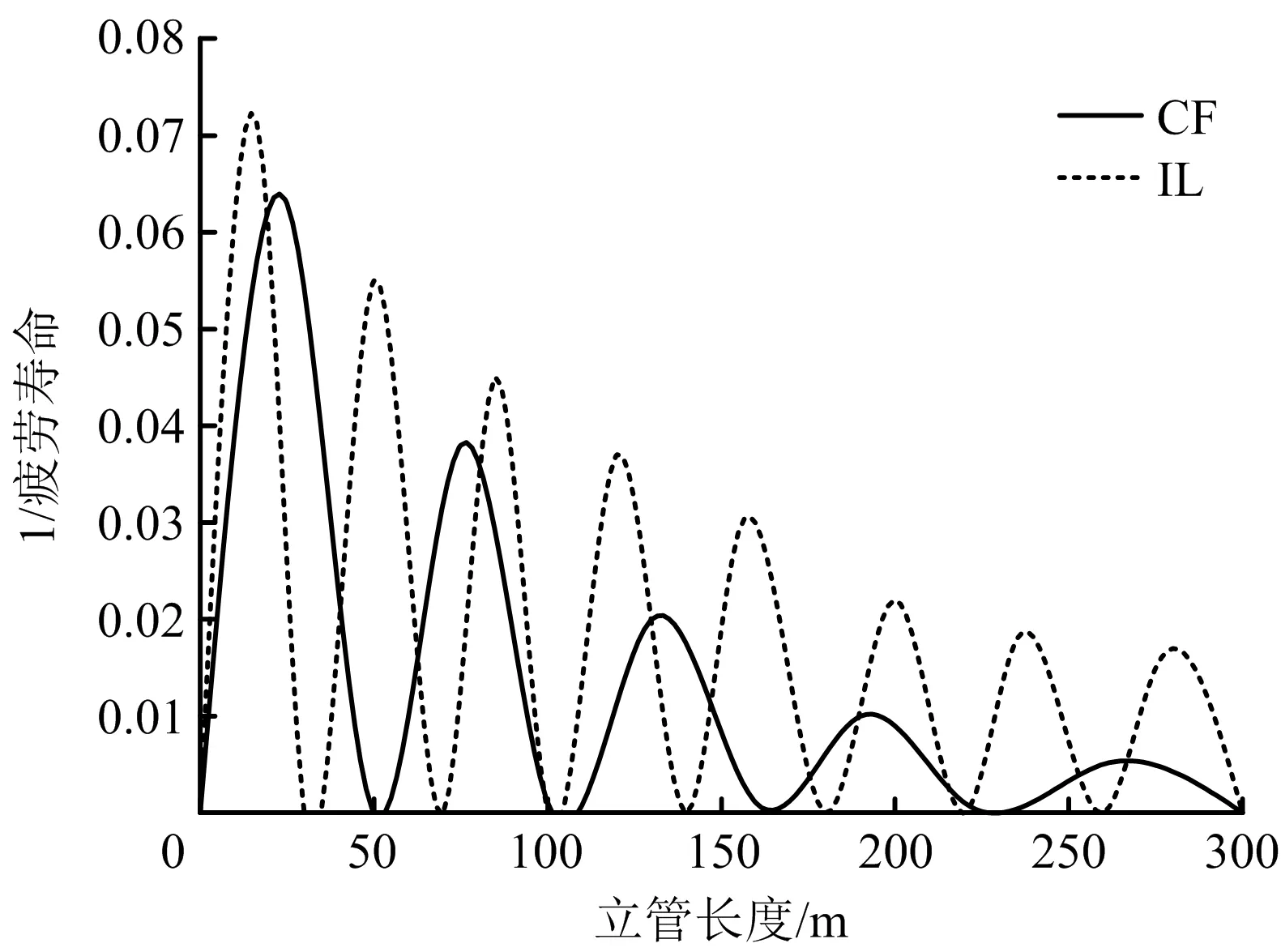
图9 立管横向和顺流向疲劳寿命Fig.9 The fatigue life of riser at the cross-flow and the in-line
从图8~9可以看出,立管IL与CF位移振动幅值处于同一数量级,内流流速对CF涡激振动影响更加敏感,振动幅值约为IL幅值0.33倍,但IL振动频率基本上是CF振动频率的2倍,因此IL涡激振动对立管的疲劳破坏同样巨大。并且对比立管IL与CF涡激振动疲劳寿命,可以发现立管CF与IL涡激振动疲劳寿命相差不大,说明IL和CF涡激振动对于立管疲劳寿命的影响同样重要,在立管振动分析中双自由度的耦合作用应该给予足够重视。
5 结论
1)立管振动位移随内流流速的增加而增加,振动频率随之减少,当降低到锁频范围会使立管产生动力放大,同时会降低立管疲劳寿命,所以实际工程设计时对内流的影响要着重考虑。
2)立管振动位移随顶张力增大而降低,证明顶张力对内流有抑制作用,实际工程中通过增大顶张力可达到消除内流影响的目的,提高立管疲劳寿命。
3)内流作用下横向涡激振动幅值约顺流向幅值0.33倍,但顺流向振动频率基本上是横向振动频率的2倍,并且通过对立管疲劳寿命对比发现顺流向和横流向涡激振动疲劳寿命大体相等,因此在立管涡激振动分析中双自由度耦合作用应该给予足够重视。

