基于SVM的通风系统故障诊断惩罚系数与核函数系数优化研究*

周启超，刘 剑，刘 丽，黄 德，邓立军，蒋清华

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105； 2.辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

0 引言

近几年，支持向量机作为经典的模式识别方法，在机器学习中占有重要的地位。文献[1]运用支持向量机根据风量特征，建立了通风系统故障诊断模型，取得了一定成果；文献[2]运用SVM方法预测矿井通风阻力系数，提高了阻力系数预测的准确率；文献[3]采用SVM评价输油管道的脆性程度；文献[4]运用SVM建立了建筑工地安全预警模型，减少施工过程中事故发生的可能。由于c，g的取值范围很大，仅凭人力穷举耗费的时间和精力是巨大的，若随机选取c，g的值可能会导致故障诊断准确率偏低，并且模型不同，SVM对应的最优c，g参数也不同，支持向量机的分类精度很大程度上取决于参数的选取，因此对参数进行优化对解决问题具有重要的意义。近些年，越来越多的方法被应用于支持向量机参数优化，如粒子群算法，网格寻优方法、花朵授粉算法、人工鱼群算法等[5-11]。文献[5]通过粒子群优化的SVM对瓦斯涌出量进行预测，但是粒子群算法收敛速度慢，容易陷入局部最优解；文献[6]采用网格搜索的方法优化最小二乘SVM，虽然获得较高的精度，但是网格寻优算法计算量大，需要的时间较长；文献[7]选取人工鱼群方法进行参数优化，具有较好的并行性，但是人工鱼群方法会出现无法准确得到最优解的情况；文献[8]提出的花朵授粉方法在寻优过程中容易陷入局部最优解，效率低。遗传算法具有良好的全局搜索能力以及收敛速度快的优点,本文利用遗传算法对SVM参数进行优化。

目前，对SVM进行参数寻优，利用优化后的SVM解决问题的研究有很多，但是解决通风系统故障的研究较少，本文利用遗传算法对SVM的惩罚参数和核函数参数进行优化，利用优化后的SVM对通风系统进行故障诊断，提升了故障诊断的准确率，对提高矿井通风安全智能化管理以及通风系统安全保障能力有一定的指导意义和建设意义。

1 参数c，g影响性分析

1.1 参数c，g意义

支持向量机在机器学习中占有重要地位，其相比于其他的分类预测算法，有着更高的准确率且具有较强的鲁棒性。SVM的基本思想是在N维空间利用结构风险最小化(SRM)原则设计具有最大间隔的最优分类面，使样本线性可分，分类平面如图1所示。

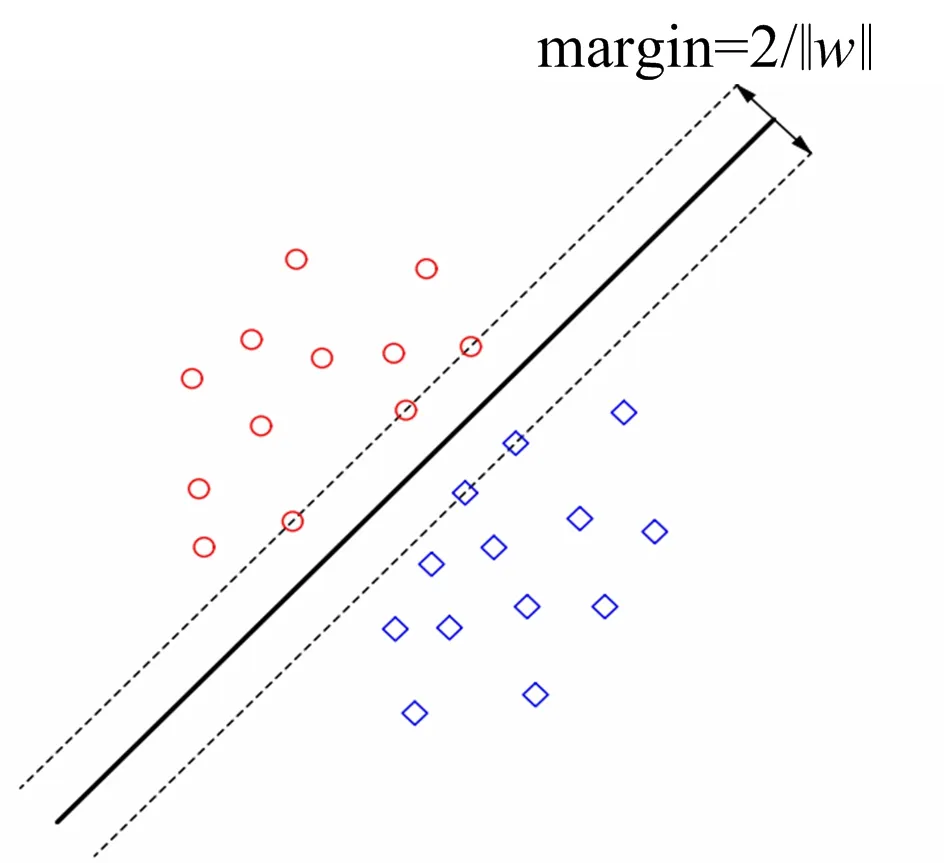
图1 分类平面示意Fig.1 Schematic diagram of the classification plane

图1中黑色实线为分类决策面，最优超平面问题就是使分类间隔margin达到最大[12]。

分类决策函数表达式[13]为：

M(x)=sgn(w·φ(x)+b)

(1)

式中：sgn(·)为符号函数；w为N维权向量；b为分类阈值；φ(x)为将x映射后的特征向量。

根据结构风险最小化原则，分类面优化问题的目标函数进一步演化为[14]：

(2)

式中：c为惩罚系数；ξi为松弛系数。

SVM进行分类的过程中，是将原本线性不可分的问题映射到高维空间变为线性可分，样本会存在噪声，使整个模型无解。式(2)中ξi的意义就是允许噪声的存在，将问题变为近似线性可分；c决定着ξi的大小，即c决定着模型对于这种误差的容忍程度，c的取值过大，ξi就会非常小，不允许噪声的存在，此时会出现过拟合的现象，降低模型的泛化能力，如图2(a)所示；若c取值过小，模型对于误差的容忍程度过大，会造成欠拟合，如图2(b)所示。

图2 过、欠拟合情况分类平面示意Fig.2 Schematic diagram of the classification of over-fitting

文献[1]使用的高斯径向基核函数运用最为广泛，无论样本大小都有较好的性能[15]，对此核函数进行分析实验，其中：

(3)

(4)

式中：δ为高斯核的带宽；g为核函数参数。

根据式(3)、式(4)可以看到，g取值的大小会直接影响整个核函数的映射性能以及支持向量的个数，如果g设的太大，会造成径向基函数(RBF)只作用于支持向量样本附近，对于未知样本分类效果很差；而如果设的过小，则会造成平滑效应太大，最终影响SVM进行故障诊断的准确率。

1.2 优化c，g取值进行故障诊断必要性分析

通常，c的取值范围为(0，100]，g的取值范围为[0,1000]，针对不同问题，c，g的取值范围不同，本文c的取值在区间(0,1.5]，g的取值在区间[0,5]。利用文献[1]中的10分支通风网络数据进行故障诊断验证优化c，g取值的必要性，其中训练样本52个，测试样本95个。

1.2.1c，g对故障诊断准确率的影响性分析

为了得到c，g变化对于准确率的具体影响，令c，g每隔0.01取值，两两组合得到75 000组准确率数据，c，g对准确率的影响具体如图3所示，得到c，g对准确率影响的规律：c越大对误差的容忍程度越小，得到的准确率越高，但是过大会出现过拟合；c过小，模型准确率降低，模型对误差容忍程度较大，出现了欠拟合的现象。g的取值小，模型准确率高，但g过小也会导致模型出现过拟合的现象。上述穷举方法耗费时间巨大，而且只能看出c，g最优取值的大致范围，很难确定最优c，g的取值。

图3 c，g取值范围准确率Fig.3 c,g the optimal value range accuracy rate map

为了清楚的看到上述现象，将图3进行局部放大，得到的结果如图4所示。

图4 局部放大图Fig.4 Partially enlarged view

1.2.2c，g参数的普适性分析

通过更换100分支样本，用前文的方法对此样本的c，g对准确率的影响规律及取值区间进行探究，c，g的取值区间发生了变化，c的取值为(0,100]，g的取值为[0,1.0]，结果如图5所示。

图5 100分支c，g取值范围准确率Fig.5 100 branch, optimal range accuracy rate map

通过和10分支通风网络c，g最优取值区间以及对故障诊断准确率的影响分析得到c，g并不具有普适性。在进行矿井通风故障诊断时，若人工选取参数，每更换不同的样本，都要进行c，g对于准确率影响规律分析及取值范围确定，工作量巨大，并且即使依靠人工选取得出最优取值范围，也无法得到最优的参数组合。

1.2.3 随机选取c，g组合故障诊断准确率

在前文确定的取值范围内，随机选取c，g进行组合，故障诊断的准确率见表1。通过结果可以判断，随机选取参数得到的准确率并不高，结果如图6所示。

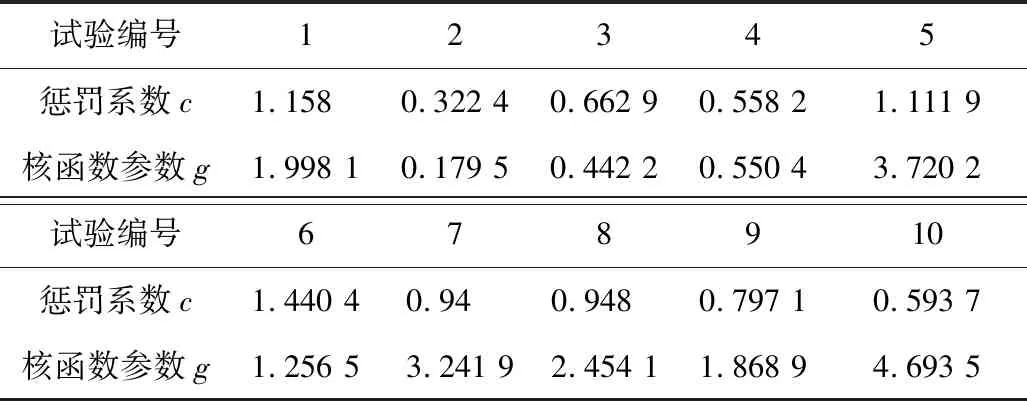
表1 c，g组合数据Table 1 c, g combination data table

图6 随机c，g组合的准确率对比Fig.6 Comparison of the accuracy of random c and g combinations

1.2.4c，g取值变化对故障诊断准确率影响程度

为了验证c，g对于准确率影响的程度，以c=1，g=1为基础，进行微小的变化，数据见表2。

表2 准确率对比Table 2 Accuracy rate comparison table

数据说明c，g的取值发生很小的变化，就会引起准确率的大幅波动，人工选取参数很难精准的得到最优结果。

综上所述，人工选取c，g的方法很难得到最优的参数组合，运用算法进行参数寻优是非常必要的。

2 基于遗传算法对c，g参数的优化

2.1 遗传算法优化c，g参数原理

遗传算法求解优化问题的基本思想是：模仿生物进化的原理，使种群不断地向目标进化。本文中个体为c，g的组合，以SVM故障诊断交叉验证准确(CVaccuracy)作为适应值，用个体的适应值作为评判标准，通过选择、交叉和变异操作，保留优秀的个体(适应值高的个体)，不断淘汰较差的个体(适应值低的个体)，最终得到准确率最高时的c，g。

2.2 遗传算法优化c，g参数实现步骤

1)染色体编码，初始种群的生成

运用遗传算法解决问题时，首先对个体进行合适的编码[16]。本文对惩罚系数c和核函数参数g采用实型编码，初始种群为随机生成。

2)适应度函数

以交叉验证准确率(CVaccuracy)作为适应值，计算如下：

(5)

accuracy=mright/m

(6)

式中：accuracy为分类准确率；v为交叉验证数；mright为测试样本中分类正确的样本个数；m为样本个数。

3)选择算子

本文采用轮盘赌法进行选择操作。具体过程如下：

设共有n个个体，每个个体的适应值为f(xi)(i=1,…,n)，被选择的概率为p(xi)，首先求得个体适应值的总和：

(7)

再计算每个个体适应值占种群总适应值的比例p(xi)，最后根据p(xi)选择个体。

p(xi)=f(xi)/SUM

(8)

4)交叉算子、变异算子

本文交叉方式为单点交叉。变异的方式有基本位变异和均匀变异[17]。本文采用基本位变异。

改进遗传算法就是将每代个体适应值与种群的平均适应值进行比较，适应值比平均适应值高的个体交叉变异率不变，适应值低的，就按照一定的数学处理进行赋值。这样可以保留较好的个体，优化适应值低的个体，使优化效果更加明显[18]。算子计算如下：

交叉概率：

Pc=0.5(maxfit-fitn)/(maxfit-meanfit)

(9)

变异概率：

Pm=0.01(maxfit-fitn)/(maxfit-meanfit)

(10)

式中：maxfit为当代种群中的最大适应值；meanfit为平均适应值；fitn为第n个个体的适应值。

3 仿真实验和结果分析

3.1 GA优化实验结果

设置遗传算法初种群规模为20。交叉概率初始为0.85，变异概率初始为0.05，以后根据个体的适应值进行自动调整。设置程序终止条件为准确率大于99%或进化代数达到50代。将改进遗传算法寻得的最优参数带入SVM进行计算，得到最终的预测准确率，经过50次迭代后，得到的适应值曲线如图7所示。

图7 改进遗传算法适应值曲线Fig.7 Improved genetic algorithm fitness curve

通过图7可以看出，GA筛选的最佳惩罚系数c为1.993 1，核函数参数g为0.056 018，此时得到的交叉验证准确率(CVaccuracy)为82.692 3%。利用参数优化后的SVM进行故障位置诊断，得到的诊断准确率可以达到97.894 7%，拟合程度如图8(a)所示，未进行参数寻优时的故障诊断结果如图8(b)所示。

通过图8可以直观的看出优化后的SVM进行故障位置诊断，预测数据与真实数据几乎完全拟合，相比较没有优化的SVM进行故障位置诊断，诊断效果有明显提升。

机器学习的过程中，都会出现过拟合的问题，为了进一步验证优化后的模型不会出现过度拟合的现象，将样本数据扩大，利用本文提出的优化模型对文献[1]中100分支复杂通风网络的4 752个训练样本，4 751个测试样本进行故障位置诊断。未优化模型(c=1，g=2)得到的故障位置诊断准确率为76.678 6%；利用遗传算法优化参数后的故障诊断准确率为78.658 2%。扩大样本后，遗传算法优化的通风故障诊断系统依旧能够保证准确率有所提升，说明在优化的过程中，未出现过拟合现象。优化前后的散点图如图9所示。

3.2 GA-SVM故障诊断有效性验证

从前文可以看出，本文采用的GA-SVM方法对于简单通风网络和复杂通风网络的故障诊断都具有一定的优化效果。为了进一步验证本文方法的有效性，更换了不同通风系统的样本数据。GA算法各参数不变，通风系统网络图和得到的结果如图10～12所示。未优化前的故障诊断准确率为73.325 1%，经过遗传算法优化后的准确率为91.935 5%。由此可以看出更换样本后，GA优化的通风系统故障诊断模型依旧可以提升诊断准确率，相比于人工选取参数的方法具有一定的优势。同时可以看出不同的样本最优的c，g参数也不同，这也证明了c，g参数不具有普适性，证明了本法的必要性。

3.3 GA-SVM故障量诊断

故障诊断是对故障位置和故障量诊断，文献[1]中未进行c，g优化时，故障量诊断效果如图13所示，利用本文方法优化参数后故障量诊断效果如图14所示，可以看到故障量诊断准确率有一定的提升。

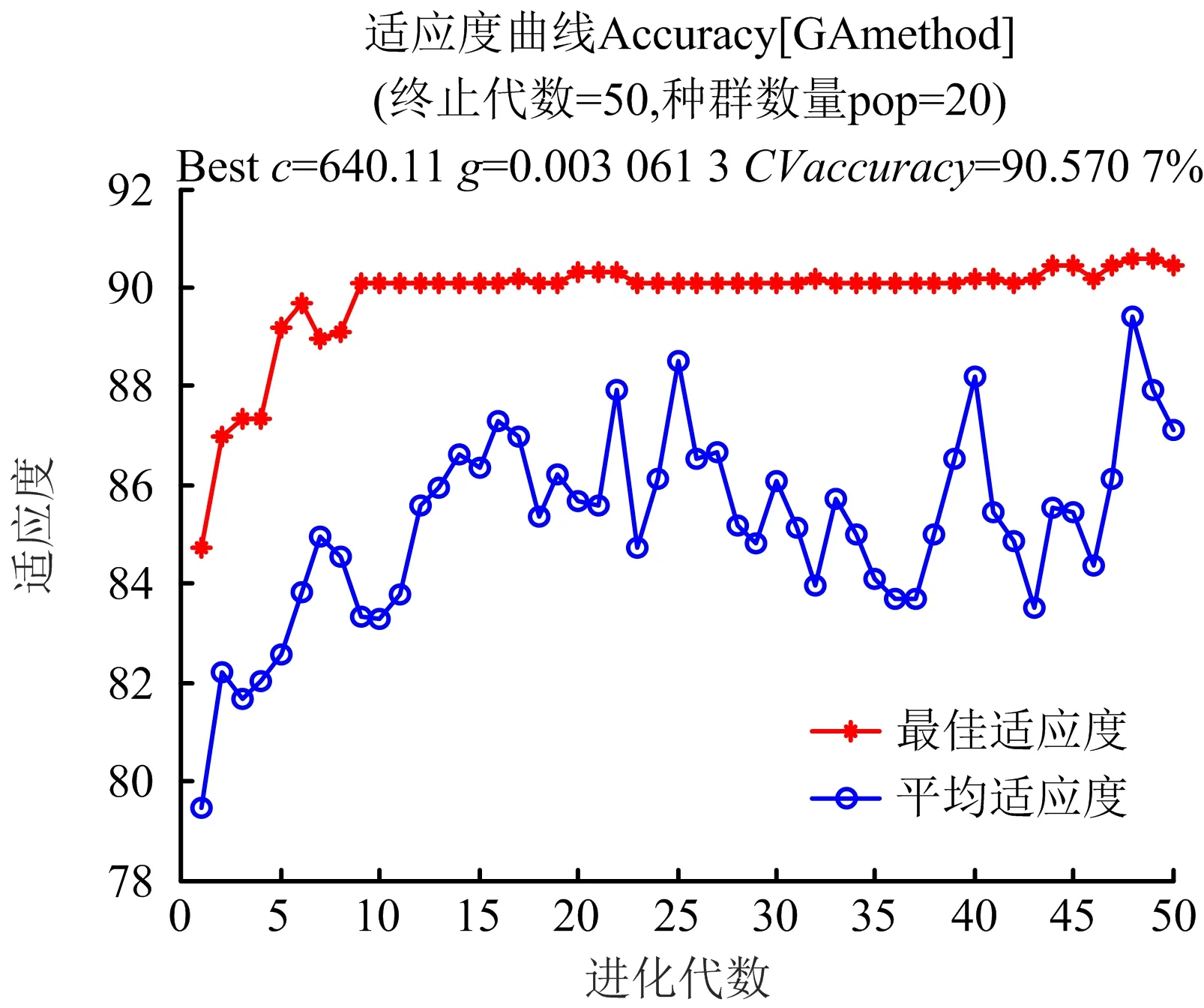
图11 验证样本遗传算法适应度曲线Fig.11 Verification of the fitness curve of the sample genetic algorithm

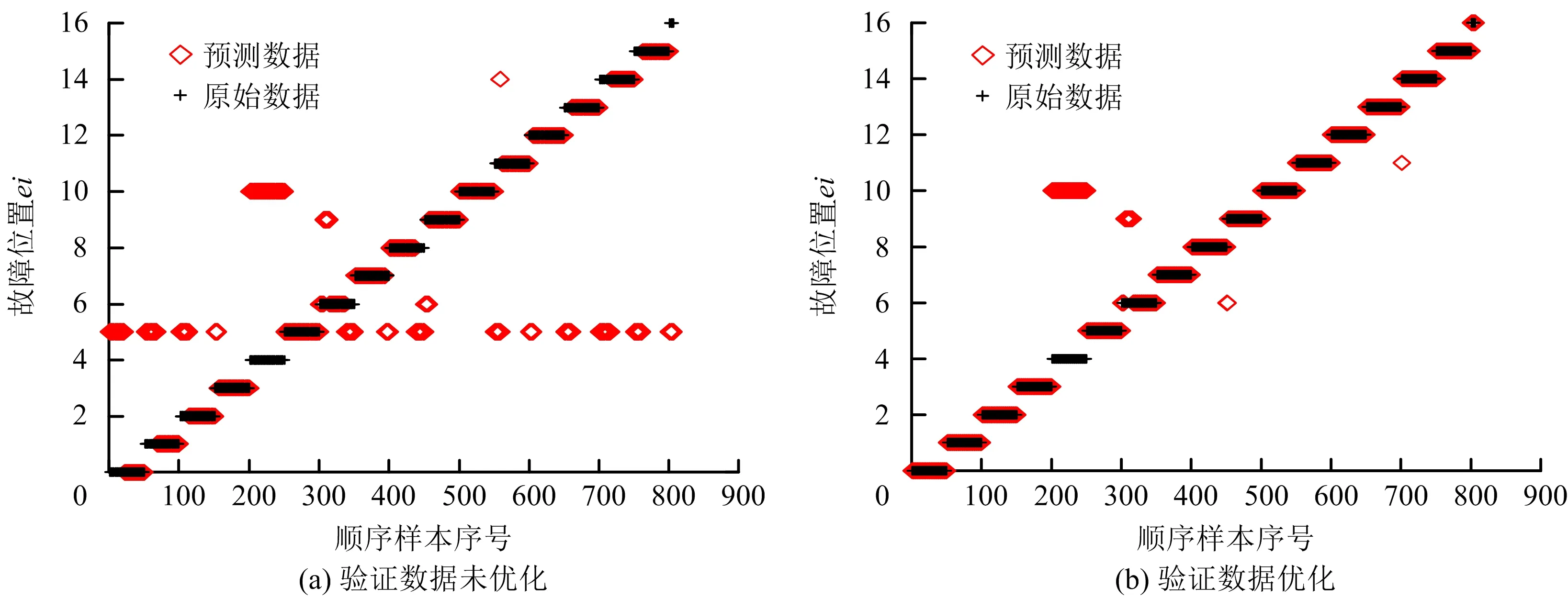
图12 验证数据散点图Fig.12 Verify data unoptimized scatter plot

图13 未优化参数故障量诊断回归效果Fig.13 Unoptimized parameter fault volume diagnosis regression effect

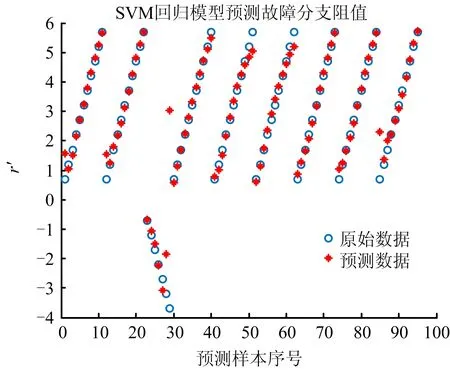
图14 GA-SVM故障量诊断回归效果Fig.14 GA-SVM fault diagnosis regression effect

4 结论

1)本文将遗传算法与SVM结合的方法应用于通风系统故障诊断，试验结果表明，经遗传算法优化的SVM通风系统故障诊断模型拥有更高的准确率。

2)优化后的惩罚系数(c)和核函数系数(g)未引起通风系统故障诊断系统的过拟合，有效的减少了拟合误差并且增强泛化能力。

3)本文所提出的优化算法对SVM参数优化后，矿井通风系统故障量诊断准确率有所提升，证明了参数优化的有效性。